14.2 三角形全等的判定 第5课时 HL 课件(共23张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 14.2 三角形全等的判定 第5课时 HL 课件(共23张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 22:31:11 | ||
图片预览





文档简介
(共23张PPT)
第14章 全等三角形
14.2 三角形全等的判定
第5课时 HL
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
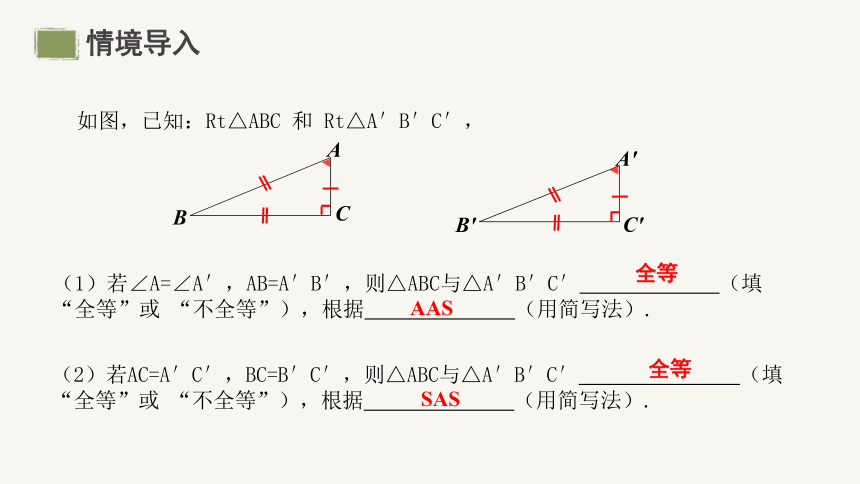
(1)若∠A=∠A′,AB=A′B′,则△ABC与△A′B′C′ (填“全等”或 “不全等”),根据 (用简写法).
(2)若AC=A′C′,BC=B′C′,则△ABC与△A′B′C′ (填“全等”或 “不全等”),根据 (用简写法).
情境导入
AAS
如图,已知:Rt△ABC 和 Rt△A′B′C′,
全等
A
B
C
A′
B′
C′
SAS
全等
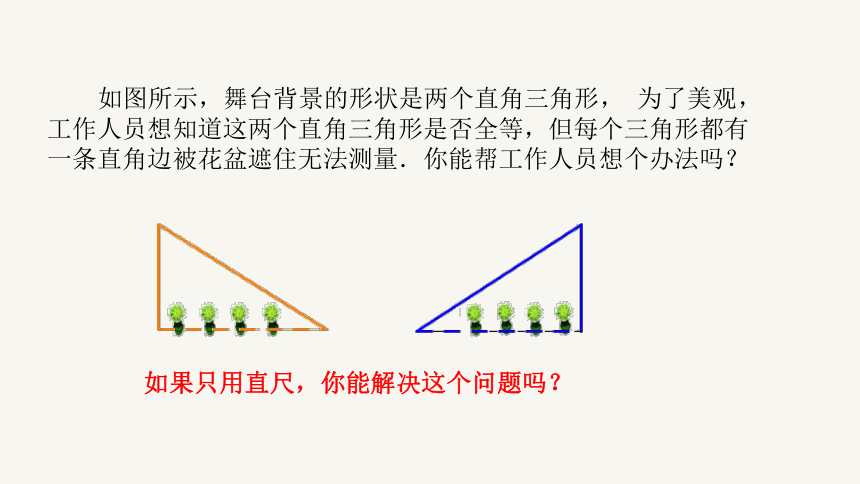
如果只用直尺,你能解决这个问题吗?
如图所示,舞台背景的形状是两个直角三角形, 为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.你能帮工作人员想个办法吗?
新知初探
贰
新知初探
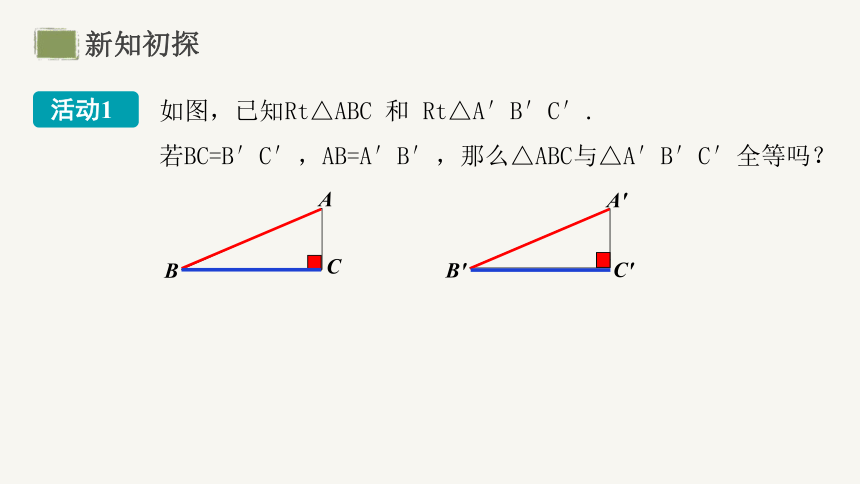
活动1
如图,已知Rt△ABC 和 Rt△A′B′C′.
若BC=B′C′,AB=A′B′,那么△ABC与△A′B′C′全等吗?
A
B
C
A′
B′
C′
问题5 点A'与点A重合吗?为什么
1个
问题1 若如果使点C与点C '重合,并且使射
线C'A'与射线CA重合,那么点B与点B'重合吗?为什么?
B
A
C
B ′
A ′
C ′
由∠C=∠C=90°可知,射线C'B'与射线CB重合.再由 B'C=BC,可知点B'与点B重合.
问题2 设点M在直角边AC(不包括端点)上,连接BM.过点M且垂直于BM的直线与线段AB相交于点M',你能说出BM,BM',BA的大小关系吗?
M
M′
AB>BM'>BM
问题3 设点N在线段CA的延长线上,连接BN,BN与AB的大小关系是怎样的?你能说出其中的道理吗?
BN>AB
问题4 在射线CA上,与点B的连线长度等于AB的点有多少个?
N
现象:两个直角三角形能重合. 说明:这两个直角三角形全等.
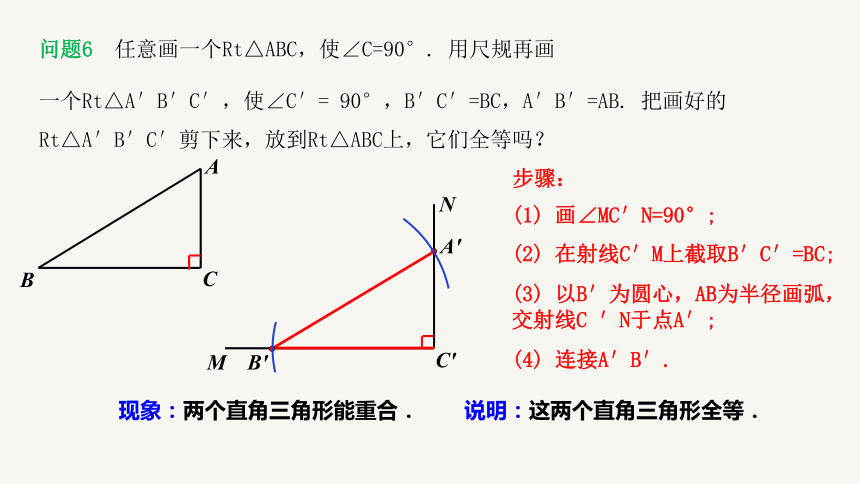
问题6 任意画一个Rt△ABC,使∠C=90°. 用尺规再画
一个Rt△A′B′C′,使∠C′= 90°,B′C′=BC,A′B′=AB. 把画好的Rt△A′B′C′剪下来,放到Rt△ABC上,它们全等吗?
步骤:
(1) 画∠MC′N=90°;
(3) 以B′为圆心,AB为半径画弧,
交射线C ′N于点A′;
(4) 连接A′B′.
(2) 在射线C′M上截取B′C′=BC;
B
A
C
B′
N
M
A′
C′
现象:两个直角三角形能重合. 说明:这两个直角三角形全等.
斜边、直角边 (“HL”):
B
A
C
B′
A′
C′
在Rt△ABC和Rt△A′B′C′ 中,
AB=A′B′,
BC=B′C′,
∴ Rt△ABC ≌ Rt△A′B′C′ (HL).
∵∠C=∠C′=90°,
斜边和一条直角边分别相等的两个直角三角形全等.
符号语言:
理解定理
范例应用
【例1】 如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.
求证:BC=AD.
在Rt△ABC和Rt△BAD中,
AB=BA ,
AC=BD,
∴ Rt△ABC≌Rt△BAD (HL).
∴BC=AD.
证明: ∵ AC⊥BC,BD⊥AD,
∴ ∠C与∠D都是直角.
?
?
任务二 直角三角形的判定方法
判定两个直角三角形全等有哪些方法?
已知条件 可选择的判定方法 需寻找的条件
一锐角对应相等 ASA或AAS 可证直角与已知锐角的夹边对应相等或者与锐角(或直角)的对边对应相等
斜边对应相等 HL或AAS 可证一直角边对应相等或证一锐角对应相等
一直角边对应相等 HL或ASA或AAS 可证斜边对应相等或证已知边相邻的锐角对应相等或证已知边所对的锐角对应相等
活动1
在Rt△ABC和Rt△A′B′C′中,
① ∠A=∠A′,
AC=A′C′,
∠C=∠C′,
Rt△ABC≌Rt△A′B′C′(ASA).
② AB=A′B′,
AC=A′C′,
Rt△ABC≌Rt△A′B′C′(HL).
在Rt△ABC和Rt△A′B′C′中,
③ AC=A′C′,
∠C=∠C′,
BC=B′C′,
Rt△ABC≌Rt△A′B′C′(SAS).
在Rt△ABC和Rt△A′B′C′中,
④ ∠C=∠C′,
∠A=∠A′,
AB=A′B′,
Rt△ABC≌Rt△A′B′C′(AAS).
分析
判定两个直角三角形全等的方法
范例应用
【例2】 已知,在Rt△ABC和Rt△A′B′C′中,∠B=∠B'=90°,有如下几个条件:①AC=A′C′,∠A=∠A′;②AC=A′C′,AB=A′B′;
③AC=A′C′,BC=B′C′;④ AB=A′B′,∠A=∠A′.其中,能判定Rt△ABC≌Rt△A′B′C′的条件的个数为( ).
A.1 B.2 C.3 D.4
根据已经学过的5种判定方法:“SSS”“SAS”、“ASA”、“AAS”、“HL”,并结合题目中的已知条件进行判断.
D
如图,AB=CD,AE⊥BC,DF⊥BC,垂足分别为E,F,CE=BF,下列结论错误的是( )
A.∠C=∠B
B.CD∥AB
C.∠A+∠D=90°
D.CF=BE
即时测评
C
当堂达标
叁
1. 判断两个直角三角形全等的方法不正确的有( )
A.两条直角边对应相等
B.斜边和一锐角对应相等
C.斜边和一条直角边对应相等
D.两个锐角对应相等
2.如图,已知AC⊥AB,AC⊥CD,要使得△ABC≌△CDA.
(1)若以“SAS”为依据,需添加条件 .
(2)若以“HL”为依据,需添加条件 .
当堂达标
D
AB=CD
BC=AD
3.如图,小明和小芳以相同的速度分别同时
从A,B出发,小明沿AC行走,小芳沿BD行走,并同时
到达C,D.若CB⊥AB,DA⊥AB,则CB与DA相等吗 为什么
解:CB=DA.
理由:由题意易知AC=BD,
∵CB⊥AB,DA⊥AB,
∴∠DAB=∠CBA=90°,
在Rt△DAB和Rt△CBA中,
∴Rt△DAB≌Rt△CBA(HL).
∴DA=CB.
4.如图所示,B、E、F、C 在同一直线上,AF⊥BC 于点F,DE⊥BC于点E,AB = DC,BE = CF,你认为 AB 平行于 CD 吗?说说你的理由.
解:平行.理由如下:
因为AF⊥BC,DE⊥BC,
所以∠AFB 和∠DEC 都是直角,
又 BE = CF,
所以BE+EF=CF+EF,即 BF = CE.
在 Rt△ABF 和 Rt△DCE 中,
AB=DC,
BF=CE,
所以Rt△ABF≌Rt△DCE(HL),
所以∠B =∠C,所以AB∥CD.
课堂小结
肆
课堂小结
SSS
SAS
ASA
AAS
斜边、直角边
(“HL”)
两个任意三角形
两个直角三角形
全等
课后作业
基础题:1.课后习题 第 11,12题。
提高题:2.请学有余力的同学完成课后习题第15题
谢
谢
第14章 全等三角形
14.2 三角形全等的判定
第5课时 HL
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
(1)若∠A=∠A′,AB=A′B′,则△ABC与△A′B′C′ (填“全等”或 “不全等”),根据 (用简写法).
(2)若AC=A′C′,BC=B′C′,则△ABC与△A′B′C′ (填“全等”或 “不全等”),根据 (用简写法).
情境导入
AAS
如图,已知:Rt△ABC 和 Rt△A′B′C′,
全等
A
B
C
A′
B′
C′
SAS
全等
如果只用直尺,你能解决这个问题吗?
如图所示,舞台背景的形状是两个直角三角形, 为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.你能帮工作人员想个办法吗?
新知初探
贰
新知初探
活动1
如图,已知Rt△ABC 和 Rt△A′B′C′.
若BC=B′C′,AB=A′B′,那么△ABC与△A′B′C′全等吗?
A
B
C
A′
B′
C′
问题5 点A'与点A重合吗?为什么
1个
问题1 若如果使点C与点C '重合,并且使射
线C'A'与射线CA重合,那么点B与点B'重合吗?为什么?
B
A
C
B ′
A ′
C ′
由∠C=∠C=90°可知,射线C'B'与射线CB重合.再由 B'C=BC,可知点B'与点B重合.
问题2 设点M在直角边AC(不包括端点)上,连接BM.过点M且垂直于BM的直线与线段AB相交于点M',你能说出BM,BM',BA的大小关系吗?
M
M′
AB>BM'>BM
问题3 设点N在线段CA的延长线上,连接BN,BN与AB的大小关系是怎样的?你能说出其中的道理吗?
BN>AB
问题4 在射线CA上,与点B的连线长度等于AB的点有多少个?
N
现象:两个直角三角形能重合. 说明:这两个直角三角形全等.
问题6 任意画一个Rt△ABC,使∠C=90°. 用尺规再画
一个Rt△A′B′C′,使∠C′= 90°,B′C′=BC,A′B′=AB. 把画好的Rt△A′B′C′剪下来,放到Rt△ABC上,它们全等吗?
步骤:
(1) 画∠MC′N=90°;
(3) 以B′为圆心,AB为半径画弧,
交射线C ′N于点A′;
(4) 连接A′B′.
(2) 在射线C′M上截取B′C′=BC;
B
A
C
B′
N
M
A′
C′
现象:两个直角三角形能重合. 说明:这两个直角三角形全等.
斜边、直角边 (“HL”):
B
A
C
B′
A′
C′
在Rt△ABC和Rt△A′B′C′ 中,
AB=A′B′,
BC=B′C′,
∴ Rt△ABC ≌ Rt△A′B′C′ (HL).
∵∠C=∠C′=90°,
斜边和一条直角边分别相等的两个直角三角形全等.
符号语言:
理解定理
范例应用
【例1】 如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.
求证:BC=AD.
在Rt△ABC和Rt△BAD中,
AB=BA ,
AC=BD,
∴ Rt△ABC≌Rt△BAD (HL).
∴BC=AD.
证明: ∵ AC⊥BC,BD⊥AD,
∴ ∠C与∠D都是直角.
?
?
任务二 直角三角形的判定方法
判定两个直角三角形全等有哪些方法?
已知条件 可选择的判定方法 需寻找的条件
一锐角对应相等 ASA或AAS 可证直角与已知锐角的夹边对应相等或者与锐角(或直角)的对边对应相等
斜边对应相等 HL或AAS 可证一直角边对应相等或证一锐角对应相等
一直角边对应相等 HL或ASA或AAS 可证斜边对应相等或证已知边相邻的锐角对应相等或证已知边所对的锐角对应相等
活动1
在Rt△ABC和Rt△A′B′C′中,
① ∠A=∠A′,
AC=A′C′,
∠C=∠C′,
Rt△ABC≌Rt△A′B′C′(ASA).
② AB=A′B′,
AC=A′C′,
Rt△ABC≌Rt△A′B′C′(HL).
在Rt△ABC和Rt△A′B′C′中,
③ AC=A′C′,
∠C=∠C′,
BC=B′C′,
Rt△ABC≌Rt△A′B′C′(SAS).
在Rt△ABC和Rt△A′B′C′中,
④ ∠C=∠C′,
∠A=∠A′,
AB=A′B′,
Rt△ABC≌Rt△A′B′C′(AAS).
分析
判定两个直角三角形全等的方法
范例应用
【例2】 已知,在Rt△ABC和Rt△A′B′C′中,∠B=∠B'=90°,有如下几个条件:①AC=A′C′,∠A=∠A′;②AC=A′C′,AB=A′B′;
③AC=A′C′,BC=B′C′;④ AB=A′B′,∠A=∠A′.其中,能判定Rt△ABC≌Rt△A′B′C′的条件的个数为( ).
A.1 B.2 C.3 D.4
根据已经学过的5种判定方法:“SSS”“SAS”、“ASA”、“AAS”、“HL”,并结合题目中的已知条件进行判断.
D
如图,AB=CD,AE⊥BC,DF⊥BC,垂足分别为E,F,CE=BF,下列结论错误的是( )
A.∠C=∠B
B.CD∥AB
C.∠A+∠D=90°
D.CF=BE
即时测评
C
当堂达标
叁
1. 判断两个直角三角形全等的方法不正确的有( )
A.两条直角边对应相等
B.斜边和一锐角对应相等
C.斜边和一条直角边对应相等
D.两个锐角对应相等
2.如图,已知AC⊥AB,AC⊥CD,要使得△ABC≌△CDA.
(1)若以“SAS”为依据,需添加条件 .
(2)若以“HL”为依据,需添加条件 .
当堂达标
D
AB=CD
BC=AD
3.如图,小明和小芳以相同的速度分别同时
从A,B出发,小明沿AC行走,小芳沿BD行走,并同时
到达C,D.若CB⊥AB,DA⊥AB,则CB与DA相等吗 为什么
解:CB=DA.
理由:由题意易知AC=BD,
∵CB⊥AB,DA⊥AB,
∴∠DAB=∠CBA=90°,
在Rt△DAB和Rt△CBA中,
∴Rt△DAB≌Rt△CBA(HL).
∴DA=CB.
4.如图所示,B、E、F、C 在同一直线上,AF⊥BC 于点F,DE⊥BC于点E,AB = DC,BE = CF,你认为 AB 平行于 CD 吗?说说你的理由.
解:平行.理由如下:
因为AF⊥BC,DE⊥BC,
所以∠AFB 和∠DEC 都是直角,
又 BE = CF,
所以BE+EF=CF+EF,即 BF = CE.
在 Rt△ABF 和 Rt△DCE 中,
AB=DC,
BF=CE,
所以Rt△ABF≌Rt△DCE(HL),
所以∠B =∠C,所以AB∥CD.
课堂小结
肆
课堂小结
SSS
SAS
ASA
AAS
斜边、直角边
(“HL”)
两个任意三角形
两个直角三角形
全等
课后作业
基础题:1.课后习题 第 11,12题。
提高题:2.请学有余力的同学完成课后习题第15题
谢
谢
同课章节目录
