14.3 角的平分线 第2课时 角平分线的判定 课件(共28张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 14.3 角的平分线 第2课时 角平分线的判定 课件(共28张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 22:34:45 | ||
图片预览






文档简介
(共28张PPT)
第14章 全等三角形
14.3 角的平分线
第2课时 角平分线的判定
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
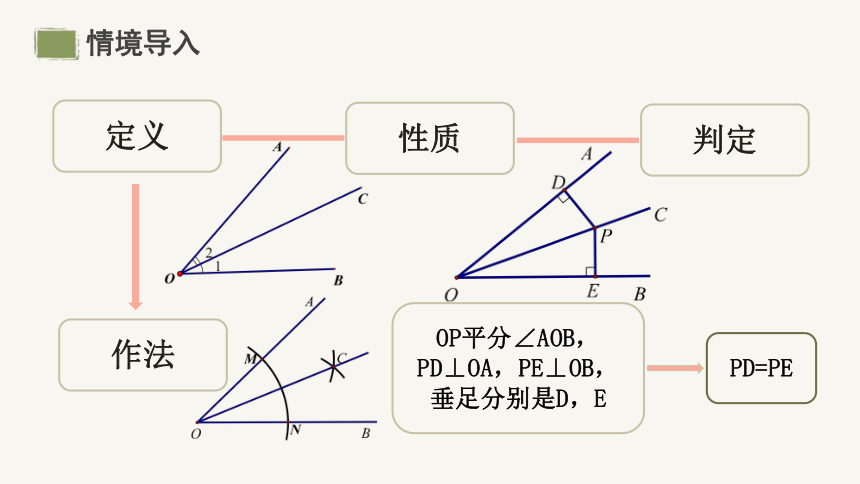
情境导入
定义
作法
性质
判定
OP平分∠AOB,
PD⊥OA,PE⊥OB,
垂足分别是D,E
PD=PE
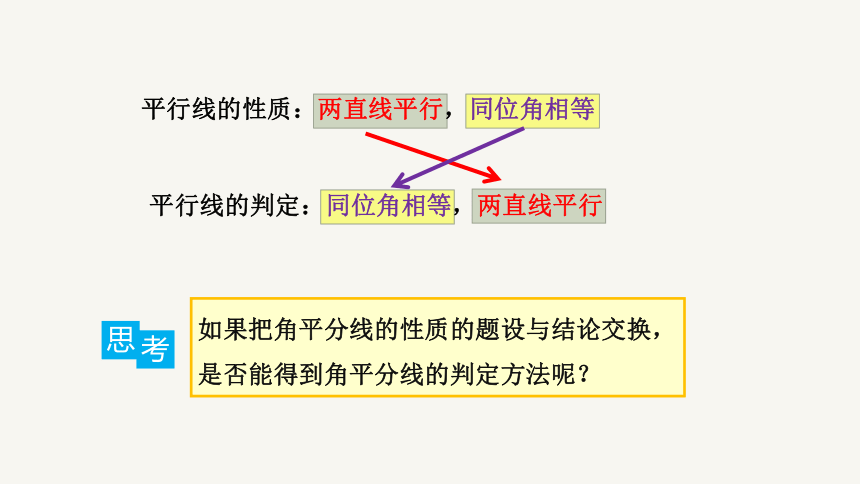
平行线的性质:两直线平行,同位角相等
平行线的判定:同位角相等,两直线平行
如果把角平分线的性质的题设与结论交换,是否能得到角平分线的判定方法呢?
思
考
新知初探
贰
新知初探
任务一 探究角平分线的判定定理
活动1 我们知道,角的平分线上的点到角两边的距离相等.反过来,交换这个性质的题设和结论,你能得到哪一个命题?这个命题还成立吗
到角两边距离相等的点在角的平分线上.
活动1
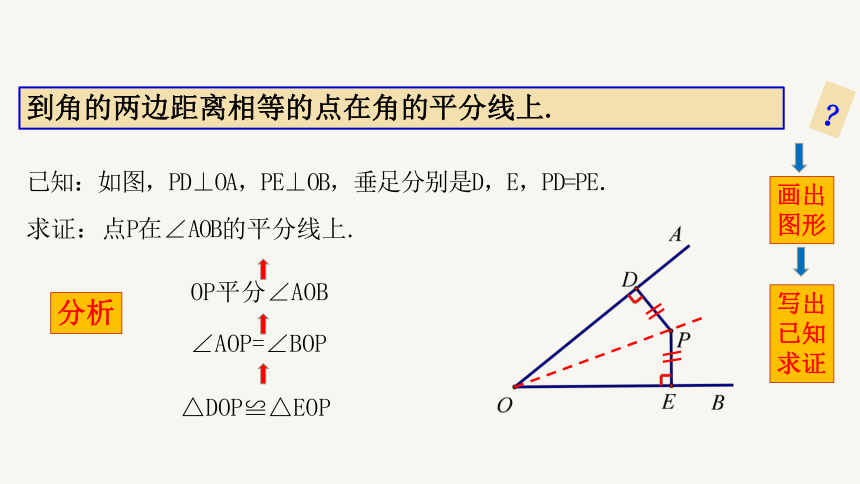
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D,E,PD=PE.
求证:点P在∠AOB的平分线上.
到角的两边距离相等的点在角的平分线上.
?
OP平分∠AOB
∠AOP=∠BOP
△DOP≌△EOP
分析
画出
图形
写出
已知
求证
已知:如图,点P在∠AOB内部,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=PE.求证:点P在∠AOB的角平分线上.
证明:
∴点P在∠AOB 角的平分线上.
在Rt△PDO和Rt△PEO 中,
(全等三角形的对应角相等).
OP=OP(公共边),
PD= PE(已知 ),
∵PD⊥OA,PE⊥OB.
∴∠PDO=∠PEO=90°,
∴Rt△PDO≌Rt△PEO( HL).
∴∠AOP=∠BOP
{
证明猜想
作射线OP,
此时点P满足PD⊥OA,PE⊥OB,垂足分别是D,E,且PD=PE,但是点P并不在∠AOB的角平分线上.
角的平分线的判定:
角的内部到角的两边距离相等的点在角的平分线上.
判定定理:
角的内部到角的两边的距离相等的点在角的平分线上.
应用所具备的条件:
(1)位置关系:点在角的内部;
(2)数量关系:该点到角两边的距离相等.
定理的作用:判断点是否在角平分线上.
符号语言:
如图,PD⊥OA,PE⊥OB,垂足分别是D,E,PD=PE,
∴点P在∠AOB的平分线上.
图形 已知条件 结论
C
1
2
P
D
E
O
C
B
1
A
2
P
D
E
OP平分∠AOB
PD⊥OA于D
PE⊥OB于E
PD=PE
P
D
E
O
B
A
P
D
E
C
角的平分线的性质和判定的区别与联系
两个定理的条件与结论是相反的
PD⊥OA于D
PE⊥OB于E
PD=PE
OP平分∠AOB
即时测评
判断以下说法正确吗?
(1)如图1,若QM =QN,则OQ 平分∠AOB;( )
判断以下说法正确吗?
(2)如图2,若QM⊥OA 于M,QN⊥OB 于N,则OQ是∠AOB 的
平分线; ( )
判断以下说法正确吗?
(3)如图3,若QM⊥OA 于M,QN⊥OB 于N,且QM=QN,则点Q在∠AOB 的平分线上.( )
双垂直+等线段
若QM⊥OA 于M,QN⊥OB 于N,且OM=ON,
∴点O在∠MQN的平分线上.
因为角的平分线上的点到角两边的距离相等;
反过来,角的内部到角两边距离相等的点在角的平分线上,所以在角的内部,角的平分线(顶点除外)可以看成到角两边距离相等的所有点的集合.
归纳总结:
范例应用
【例题】 如图,△ABC的角平分线BM,CN相交于点P.
求证:(1)点P到三边AB,BC,CA的距离相等;
D
E
F
A
B
C
P
N
M
BP平分∠ABC,
PD⊥AB,PE⊥BC,
垂足是D,E,
PD=PE
CP平分∠ACB,
PE⊥BC,PF⊥AC ,垂足是E,F,
PE=PF
PD=PE=PF
范例应用
【例题】 如图,△ABC的角平分线BM,CN相交于点P.
求证:(1)点P到三边AB,BC,CA的距离相等;
D
E
F
A
B
C
P
N
M
证明:(1)过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵ BM是△ABC的角平分线, 点P在BM上,
∴ PD=PE .
同理 PE=PF .
∴ PD=PE=PF .
即点P到三边AB,BC,CA的距离相等.
【例题】 如图,△ABC的角平分线BM,CN相交于点P.
求证:(2) △ABC的三条角平分线交于一点.
D
E
F
A
B
C
P
N
M
证明:(2)由(1)得,点P到边AB,CA的距离相等,
∴点P在∠A的平分线上,
∴△ABC的三条角平分线交于一点.
归纳总结:三角形三个内角的平分线交于一点,而且这个点到三边的距离相等.
当堂达标
叁
1. 如图,∠AOB=70°,QC⊥OA于C,QD⊥OB于D,若QC=QD,则∠AOQ的度数为( )
A、20° B、30° C、35° D、40°
当堂达标
C
2.三条公路将A、B、C三个村庄连成一个如图的三角形区域,如果在这个区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,那么这个集贸市场应建的位置是( )
A.三条高线的交点 B.三条中线的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
C
解:QM=QN.理由如下:
∵PE⊥OA,PF⊥OB,PE=PF,
∴OP平分∠AOB,
∵QM⊥OA,QN⊥OB,
∴QM=QN.
3.如图,点P是∠AOB内部的一点,PE⊥OA,PF⊥OB,垂足分别为点E,点F,且PE=PF.点Q是OP上的任意一点,QM⊥OA,QN⊥OB,垂足分别为点M和点N,QM与QN相等吗?为什么?
4.如图所示,点P是△ABC的外角∠CBE和外角∠BCF的平分线的交点,求证:AP平分∠BAC.
证明:作PQ⊥BC,PM⊥AE,PN⊥AF,垂足分别为Q,M,N.
因为P点在∠CBE和∠BCF的平分线上,
所以PM = PQ,PN = PQ,
所以PM = PN.
N
Q
M
又PM⊥AE,PN⊥AF,
所以 AP平分∠BAC.
课堂小结
肆
课堂小结
角平分线
的判定定理
内容
角的内部到角两边距离相等的点在这个角的平分线上
作用
判断一个点是否在角的平分线上
结论
三角形的角平分线相交于内部一点
课后作业
基础题:1.课后习题 第 3,6题。
提高题:2.请学有余力的同学完成课后习题第8题
谢
谢
第14章 全等三角形
14.3 角的平分线
第2课时 角平分线的判定
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
定义
作法
性质
判定
OP平分∠AOB,
PD⊥OA,PE⊥OB,
垂足分别是D,E
PD=PE
平行线的性质:两直线平行,同位角相等
平行线的判定:同位角相等,两直线平行
如果把角平分线的性质的题设与结论交换,是否能得到角平分线的判定方法呢?
思
考
新知初探
贰
新知初探
任务一 探究角平分线的判定定理
活动1 我们知道,角的平分线上的点到角两边的距离相等.反过来,交换这个性质的题设和结论,你能得到哪一个命题?这个命题还成立吗
到角两边距离相等的点在角的平分线上.
活动1
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D,E,PD=PE.
求证:点P在∠AOB的平分线上.
到角的两边距离相等的点在角的平分线上.
?
OP平分∠AOB
∠AOP=∠BOP
△DOP≌△EOP
分析
画出
图形
写出
已知
求证
已知:如图,点P在∠AOB内部,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=PE.求证:点P在∠AOB的角平分线上.
证明:
∴点P在∠AOB 角的平分线上.
在Rt△PDO和Rt△PEO 中,
(全等三角形的对应角相等).
OP=OP(公共边),
PD= PE(已知 ),
∵PD⊥OA,PE⊥OB.
∴∠PDO=∠PEO=90°,
∴Rt△PDO≌Rt△PEO( HL).
∴∠AOP=∠BOP
{
证明猜想
作射线OP,
此时点P满足PD⊥OA,PE⊥OB,垂足分别是D,E,且PD=PE,但是点P并不在∠AOB的角平分线上.
角的平分线的判定:
角的内部到角的两边距离相等的点在角的平分线上.
判定定理:
角的内部到角的两边的距离相等的点在角的平分线上.
应用所具备的条件:
(1)位置关系:点在角的内部;
(2)数量关系:该点到角两边的距离相等.
定理的作用:判断点是否在角平分线上.
符号语言:
如图,PD⊥OA,PE⊥OB,垂足分别是D,E,PD=PE,
∴点P在∠AOB的平分线上.
图形 已知条件 结论
C
1
2
P
D
E
O
C
B
1
A
2
P
D
E
OP平分∠AOB
PD⊥OA于D
PE⊥OB于E
PD=PE
P
D
E
O
B
A
P
D
E
C
角的平分线的性质和判定的区别与联系
两个定理的条件与结论是相反的
PD⊥OA于D
PE⊥OB于E
PD=PE
OP平分∠AOB
即时测评
判断以下说法正确吗?
(1)如图1,若QM =QN,则OQ 平分∠AOB;( )
判断以下说法正确吗?
(2)如图2,若QM⊥OA 于M,QN⊥OB 于N,则OQ是∠AOB 的
平分线; ( )
判断以下说法正确吗?
(3)如图3,若QM⊥OA 于M,QN⊥OB 于N,且QM=QN,则点Q在∠AOB 的平分线上.( )
双垂直+等线段
若QM⊥OA 于M,QN⊥OB 于N,且OM=ON,
∴点O在∠MQN的平分线上.
因为角的平分线上的点到角两边的距离相等;
反过来,角的内部到角两边距离相等的点在角的平分线上,所以在角的内部,角的平分线(顶点除外)可以看成到角两边距离相等的所有点的集合.
归纳总结:
范例应用
【例题】 如图,△ABC的角平分线BM,CN相交于点P.
求证:(1)点P到三边AB,BC,CA的距离相等;
D
E
F
A
B
C
P
N
M
BP平分∠ABC,
PD⊥AB,PE⊥BC,
垂足是D,E,
PD=PE
CP平分∠ACB,
PE⊥BC,PF⊥AC ,垂足是E,F,
PE=PF
PD=PE=PF
范例应用
【例题】 如图,△ABC的角平分线BM,CN相交于点P.
求证:(1)点P到三边AB,BC,CA的距离相等;
D
E
F
A
B
C
P
N
M
证明:(1)过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵ BM是△ABC的角平分线, 点P在BM上,
∴ PD=PE .
同理 PE=PF .
∴ PD=PE=PF .
即点P到三边AB,BC,CA的距离相等.
【例题】 如图,△ABC的角平分线BM,CN相交于点P.
求证:(2) △ABC的三条角平分线交于一点.
D
E
F
A
B
C
P
N
M
证明:(2)由(1)得,点P到边AB,CA的距离相等,
∴点P在∠A的平分线上,
∴△ABC的三条角平分线交于一点.
归纳总结:三角形三个内角的平分线交于一点,而且这个点到三边的距离相等.
当堂达标
叁
1. 如图,∠AOB=70°,QC⊥OA于C,QD⊥OB于D,若QC=QD,则∠AOQ的度数为( )
A、20° B、30° C、35° D、40°
当堂达标
C
2.三条公路将A、B、C三个村庄连成一个如图的三角形区域,如果在这个区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,那么这个集贸市场应建的位置是( )
A.三条高线的交点 B.三条中线的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
C
解:QM=QN.理由如下:
∵PE⊥OA,PF⊥OB,PE=PF,
∴OP平分∠AOB,
∵QM⊥OA,QN⊥OB,
∴QM=QN.
3.如图,点P是∠AOB内部的一点,PE⊥OA,PF⊥OB,垂足分别为点E,点F,且PE=PF.点Q是OP上的任意一点,QM⊥OA,QN⊥OB,垂足分别为点M和点N,QM与QN相等吗?为什么?
4.如图所示,点P是△ABC的外角∠CBE和外角∠BCF的平分线的交点,求证:AP平分∠BAC.
证明:作PQ⊥BC,PM⊥AE,PN⊥AF,垂足分别为Q,M,N.
因为P点在∠CBE和∠BCF的平分线上,
所以PM = PQ,PN = PQ,
所以PM = PN.
N
Q
M
又PM⊥AE,PN⊥AF,
所以 AP平分∠BAC.
课堂小结
肆
课堂小结
角平分线
的判定定理
内容
角的内部到角两边距离相等的点在这个角的平分线上
作用
判断一个点是否在角的平分线上
结论
三角形的角平分线相交于内部一点
课后作业
基础题:1.课后习题 第 3,6题。
提高题:2.请学有余力的同学完成课后习题第8题
谢
谢
同课章节目录
