15.1.2 线段的垂直平分线 第1课时 线段垂直平分线的性质与判定 课件(共37张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 15.1.2 线段的垂直平分线 第1课时 线段垂直平分线的性质与判定 课件(共37张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 22:39:00 | ||
图片预览





文档简介
(共37张PPT)
第15章 轴对称
15.1.2 线段的垂直平分线
第1课时 线段垂直平分线的性质与判定
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
1.轴对称有什么性质?
2.线段是轴对称图形吗?它的对称轴是什么?
3.什么叫线段的垂直平分线?
经过线段的中点并且垂直于这条线段的直线,
叫作这条线段的垂直平分线.
新知初探
贰
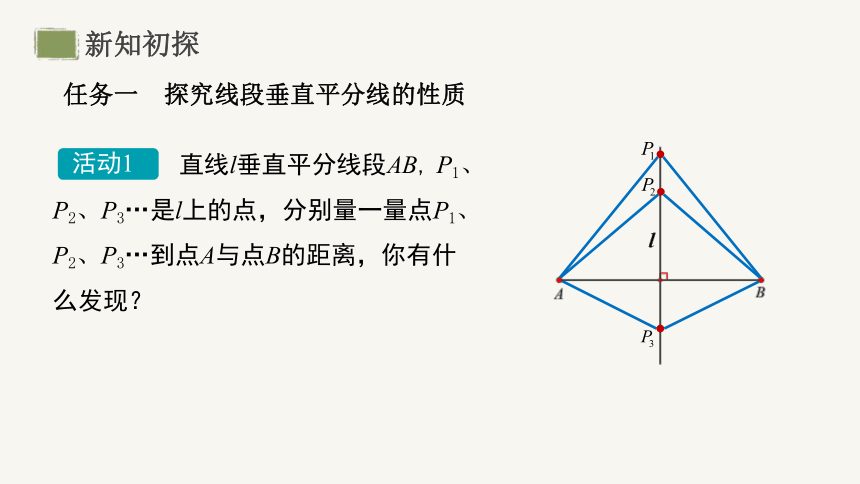
直线l垂直平分线段AB, P1、P2、P3…是l上的点,分别量一量点P1、P2、P3…到点A与点B的距离,你有什么发现?
新知初探
任务一 探究线段垂直平分线的性质
活动1
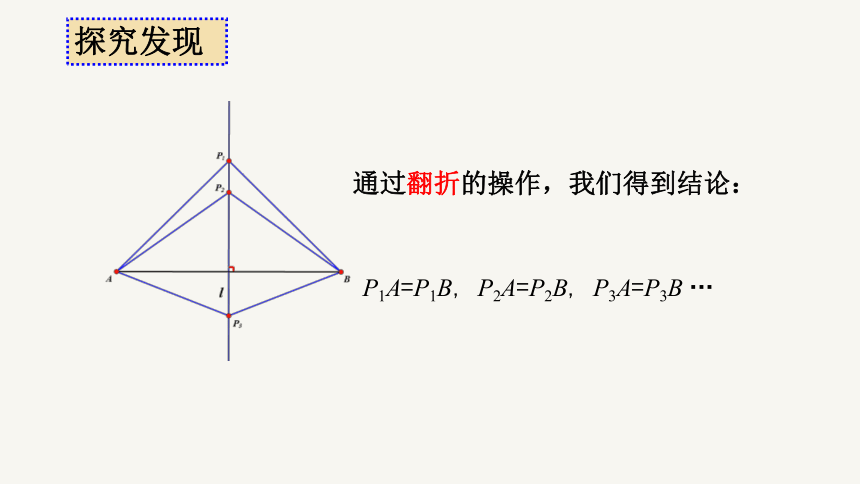
通过翻折的操作,我们得到结论:
P1A=P1B, P2A=P2B, P3A=P3B …
探究发现
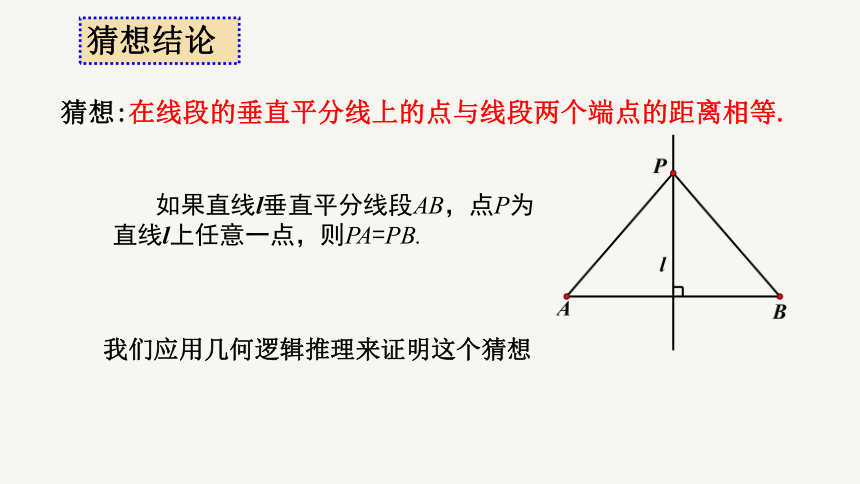
猜想:在线段的垂直平分线上的点与线段两个端点的距离相等.
如果直线l垂直平分线段AB,点P为直线l上任意一点,则PA=PB.
我们应用几何逻辑推理来证明这个猜想
猜想结论
(SAS).
∵
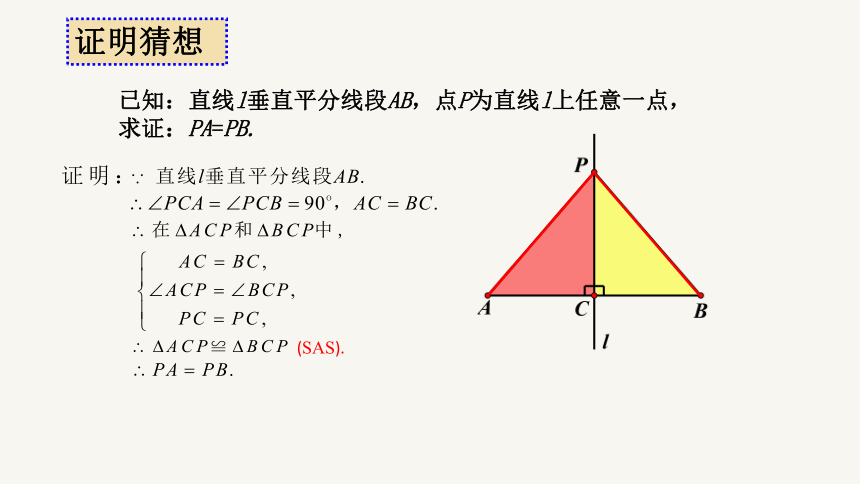
已知:直线l垂直平分线段AB,点P为直线l上任意一点,
求证:PA=PB.
证明猜想
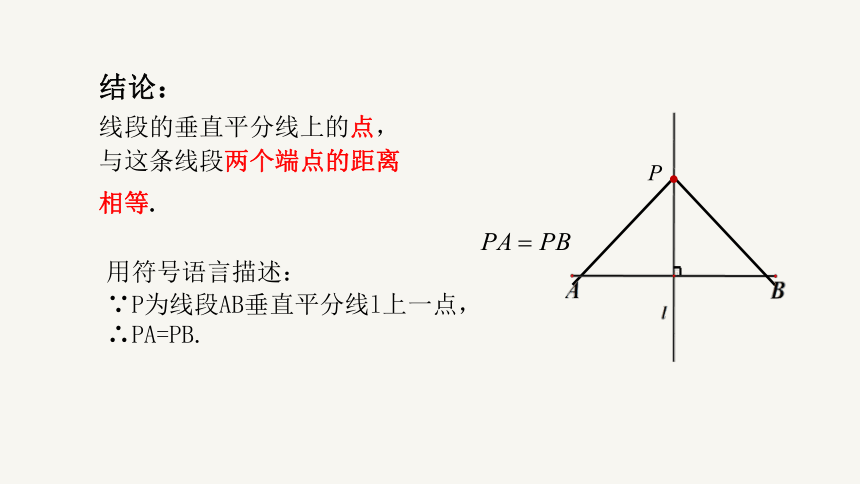
线段的垂直平分线上的点,
与这条线段两个端点的距离
相等.
结论:
用符号语言描述:
∵P为线段AB垂直平分线l上一点,
∴PA=PB.
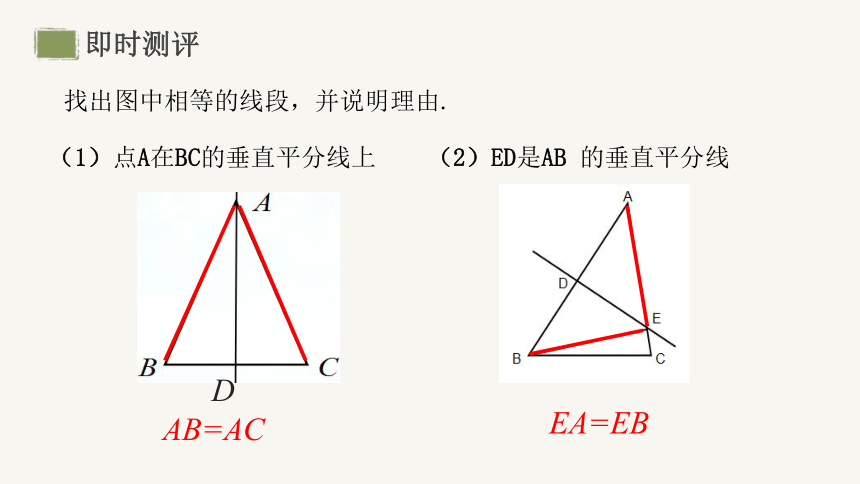
即时测评
找出图中相等的线段,并说明理由.
(1)点A在BC的垂直平分线上
D
AB=AC
(2)ED是AB 的垂直平分线
EA=EB
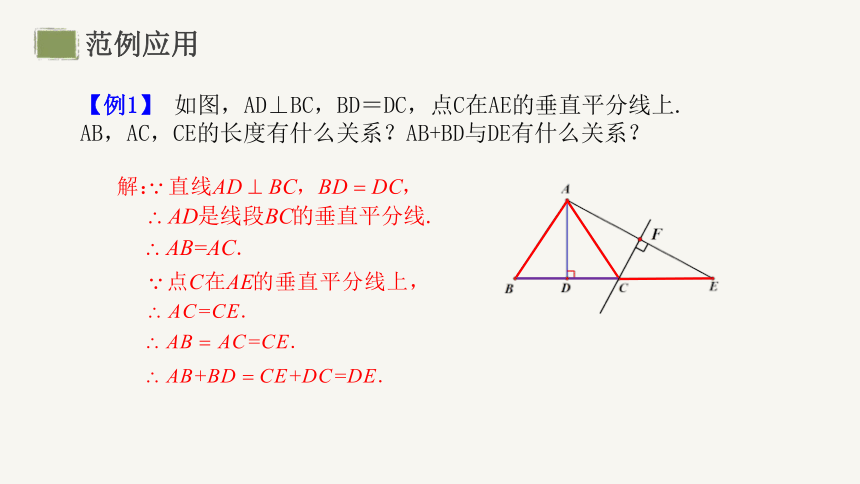
范例应用
【例1】 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上.
AB,AC,CE的长度有什么关系?AB+BD与DE有什么关系?
活动2
我们已经知道线段垂直平分线上的所有点与这条线段两个端点的距离相等.反过来,“与线段两个端点距离相等的点”在这条线段的垂直平分线上吗?
想一想
猜想:与一条线段两个端点距离相等的点在这
条线段的垂直平分线上.
如果PA=PB,则点P在线段AB的垂直平分线上.
我们应用几何逻辑推理来证明这个猜想
猜想结论
证明猜想
已知: PA=PB,
求证:点P为线段AB垂直平分线上的点.
注意:题设中没有明确说明点P和线段AB的位置关系.
第一种分类:点P在线段AB上
第二种分类:点P在线段AB外
证明:
(1)如图,当点P在线段AB上时,若PA=PB,则点P为线段AB的中点,
点P必在线段AB的垂直平分线上.
已知: PA=PB,
求证:点P为线段AB垂直平分线上的点.
证明猜想
(2)如图,当点P在线段AB外,
已知: PA=PB,
求证:点P为线段AB垂直平分线上的点.
方法点拨:我们需要过点P作出一条辅助线,然后证明这条辅助线是线段AB的垂直平分线.
注意:这条辅助线不能同时体现出垂直与平分两个性质,所以要让辅助线满足其中一个性质,再以此作为条件通过证明得到另外一个性质.因此,当点P在线段AB外时,我们有两种证明思路:
证明猜想
证明思路1:过点P作AB边的高PD,然后证明PD为AB边的中线.简称:“作垂直,证平分”.
证明思路2:过点P作AB边的中线PD,然后证
明PD为AB边的高.简称:“作平分,证垂直”.
证明猜想
证明猜想
(HL).
“作垂直,证平分”的具体证明过程:
已知: PA=PB,
求证:点P为线段AB垂直平分线上的点.
证明猜想
(SSS).
∵
“作平分,证垂直”的具体证明过程:
已知: PA=PB,
求证:点P为线段AB垂直平分线上的点.
与线段的两个端点的距离相等的点,
在这条线段的垂直平分线上
结论:
用符号语言描述:
∵ PA=PB,
∴ P为线段AB垂直平分线l上一点.
这些点能组成什么几何图形?
你能再找一些到线段AB 两端点的距离相等的点吗?能找到多少个到线段AB 两端点距离相等的点?
在线段AB 的垂直平分线l 上的点与A,B 的距离都相等;反过来,与A,B 的距离相等的点都在直线l上,所以直线l 可以看成与两点A、B 的距离相等的所有点的集合.
P
A
B
C
l
试一试:
范例应用
∵
∵
【例2】 如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
任务二 逆命题与逆定理
分析上面关于线段的垂直平分线的两个命题,它们的题设和结论有什么关系?你还学习过其他具有类似关系的命题吗?
活动1
思
考
这两个命题的题设、结论正好相反,我们把具有这种关系的两个命题叫作互逆命题,如果把其中一个叫作原命题,那么另一个叫作它的逆命题.
归纳总结:
问题1 写出下列各命题的逆命题,这些逆命题成立吗?
(1)同旁内角互补,两直线平行;
逆命题:两直线平行,同旁内角互补.成立.
(2)对顶角相等;
逆命题:如果两个角相等,那么这两个角是对顶角.不成立.
(3)全等三角形的对应边相等;
逆命题:三条边对应相等的两个三角形全等.成立.
(4)如果两个实数相等,那么它们的平方相等.
逆命题:如果两个实数的平方相等,那么这两个实数相等.不成立.
一般地,原命题成立时,它的逆命题可能成立,也可能不成立,
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫作互逆定理,其中一个定理叫作另一个定理的逆定理.
归纳总结:
问题2 你能举出几个互逆定理的例子吗.
两直线平行,内错角相等”和“内错角相等,两直线平行”.
“线段垂直平分线上的点与这条线段两个端点的距离相等”和“与线段两个端点距离相等的点在这条线段的垂直平分线上”.
你还能举出其它例子吗?
下列说法正确的是( )
A.命题一定有逆命题
B.所有的定理一定有逆定理
C.真命题的逆命题一定是真命题
D.假命题的逆命题一定是假命题
即时测评
A
当堂达标
叁
当堂达标
1.如图所示,AC=AD,BC=BD,则下列说法正确的是( )
A.AB垂直平分CD; B .CD垂直平分AB ;
C.AB与CD互相垂直平分; D.CD平分∠ ACB .
2.到三角形三个顶点的距离相等的点是( )
A.三条角平分线的交点 B.三边垂直平分线的交点
C.三边高线的交点 D.没有这样的点
A
B
3.如图,已知在△ABC中,DE是BC的垂直平分线,垂足为E,交AC于点D,若AB=6,AC=9,则△ABD的周长是 .
4.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上.若AB=5cm,BC=6cm,则AC= ,DE= .
8cm
15
5cm
A
B
O
E
D
C
证明:
因为OE平分∠AOB,EC⊥OA,ED⊥OB,
所以DE=CE.
∠DOE=∠COE,
因为EC⊥OA,ED⊥OB,所以∠ODE=∠OCE=90°,
所以△OED≌△OEC(AAS),所以OC=OD;
所以 OE是CD的垂直平分线.
5.如图所示,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D,连接CD.求证:OE是CD的垂直平分线.
解:(1)逆命题是全等三角形的三边对应相等,真命题,是互逆定理.
(2)逆命题是三个角对应相等的两个三角形全等,假命题.
(4)逆命题是同旁内角互补,两直线平行,真命题,是互逆定理.
6.写出下列命题的逆命题,并判断其真假,指出其中的互逆定理.
(1)三边对应相等的两个三角形全等;
(2)全等三角形的三个角对应相等;
(3)两直线平行,同旁内角互补.
课堂小结
肆
课堂小结
线段垂直平分线上的点与这条线段两个端点的距离相等.
PA=PB
点P在线段AB的垂直平分线上.
与线段两个端点距离相等的点在这条线段的垂直平分线上.
线段垂直平分线上的点与线段两个端点的距离相等.
与线段两个端点距离相等的点在这条线段的垂直平分线上.
原命题
逆命题
课后作业
基础题:1.课后习题 第 4,5,6题。
提高题:2.请学有余力的同学完成课后习题第13题
谢
谢
第15章 轴对称
15.1.2 线段的垂直平分线
第1课时 线段垂直平分线的性质与判定
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
1.轴对称有什么性质?
2.线段是轴对称图形吗?它的对称轴是什么?
3.什么叫线段的垂直平分线?
经过线段的中点并且垂直于这条线段的直线,
叫作这条线段的垂直平分线.
新知初探
贰
直线l垂直平分线段AB, P1、P2、P3…是l上的点,分别量一量点P1、P2、P3…到点A与点B的距离,你有什么发现?
新知初探
任务一 探究线段垂直平分线的性质
活动1
通过翻折的操作,我们得到结论:
P1A=P1B, P2A=P2B, P3A=P3B …
探究发现
猜想:在线段的垂直平分线上的点与线段两个端点的距离相等.
如果直线l垂直平分线段AB,点P为直线l上任意一点,则PA=PB.
我们应用几何逻辑推理来证明这个猜想
猜想结论
(SAS).
∵
已知:直线l垂直平分线段AB,点P为直线l上任意一点,
求证:PA=PB.
证明猜想
线段的垂直平分线上的点,
与这条线段两个端点的距离
相等.
结论:
用符号语言描述:
∵P为线段AB垂直平分线l上一点,
∴PA=PB.
即时测评
找出图中相等的线段,并说明理由.
(1)点A在BC的垂直平分线上
D
AB=AC
(2)ED是AB 的垂直平分线
EA=EB
范例应用
【例1】 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上.
AB,AC,CE的长度有什么关系?AB+BD与DE有什么关系?
活动2
我们已经知道线段垂直平分线上的所有点与这条线段两个端点的距离相等.反过来,“与线段两个端点距离相等的点”在这条线段的垂直平分线上吗?
想一想
猜想:与一条线段两个端点距离相等的点在这
条线段的垂直平分线上.
如果PA=PB,则点P在线段AB的垂直平分线上.
我们应用几何逻辑推理来证明这个猜想
猜想结论
证明猜想
已知: PA=PB,
求证:点P为线段AB垂直平分线上的点.
注意:题设中没有明确说明点P和线段AB的位置关系.
第一种分类:点P在线段AB上
第二种分类:点P在线段AB外
证明:
(1)如图,当点P在线段AB上时,若PA=PB,则点P为线段AB的中点,
点P必在线段AB的垂直平分线上.
已知: PA=PB,
求证:点P为线段AB垂直平分线上的点.
证明猜想
(2)如图,当点P在线段AB外,
已知: PA=PB,
求证:点P为线段AB垂直平分线上的点.
方法点拨:我们需要过点P作出一条辅助线,然后证明这条辅助线是线段AB的垂直平分线.
注意:这条辅助线不能同时体现出垂直与平分两个性质,所以要让辅助线满足其中一个性质,再以此作为条件通过证明得到另外一个性质.因此,当点P在线段AB外时,我们有两种证明思路:
证明猜想
证明思路1:过点P作AB边的高PD,然后证明PD为AB边的中线.简称:“作垂直,证平分”.
证明思路2:过点P作AB边的中线PD,然后证
明PD为AB边的高.简称:“作平分,证垂直”.
证明猜想
证明猜想
(HL).
“作垂直,证平分”的具体证明过程:
已知: PA=PB,
求证:点P为线段AB垂直平分线上的点.
证明猜想
(SSS).
∵
“作平分,证垂直”的具体证明过程:
已知: PA=PB,
求证:点P为线段AB垂直平分线上的点.
与线段的两个端点的距离相等的点,
在这条线段的垂直平分线上
结论:
用符号语言描述:
∵ PA=PB,
∴ P为线段AB垂直平分线l上一点.
这些点能组成什么几何图形?
你能再找一些到线段AB 两端点的距离相等的点吗?能找到多少个到线段AB 两端点距离相等的点?
在线段AB 的垂直平分线l 上的点与A,B 的距离都相等;反过来,与A,B 的距离相等的点都在直线l上,所以直线l 可以看成与两点A、B 的距离相等的所有点的集合.
P
A
B
C
l
试一试:
范例应用
∵
∵
【例2】 如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
任务二 逆命题与逆定理
分析上面关于线段的垂直平分线的两个命题,它们的题设和结论有什么关系?你还学习过其他具有类似关系的命题吗?
活动1
思
考
这两个命题的题设、结论正好相反,我们把具有这种关系的两个命题叫作互逆命题,如果把其中一个叫作原命题,那么另一个叫作它的逆命题.
归纳总结:
问题1 写出下列各命题的逆命题,这些逆命题成立吗?
(1)同旁内角互补,两直线平行;
逆命题:两直线平行,同旁内角互补.成立.
(2)对顶角相等;
逆命题:如果两个角相等,那么这两个角是对顶角.不成立.
(3)全等三角形的对应边相等;
逆命题:三条边对应相等的两个三角形全等.成立.
(4)如果两个实数相等,那么它们的平方相等.
逆命题:如果两个实数的平方相等,那么这两个实数相等.不成立.
一般地,原命题成立时,它的逆命题可能成立,也可能不成立,
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫作互逆定理,其中一个定理叫作另一个定理的逆定理.
归纳总结:
问题2 你能举出几个互逆定理的例子吗.
两直线平行,内错角相等”和“内错角相等,两直线平行”.
“线段垂直平分线上的点与这条线段两个端点的距离相等”和“与线段两个端点距离相等的点在这条线段的垂直平分线上”.
你还能举出其它例子吗?
下列说法正确的是( )
A.命题一定有逆命题
B.所有的定理一定有逆定理
C.真命题的逆命题一定是真命题
D.假命题的逆命题一定是假命题
即时测评
A
当堂达标
叁
当堂达标
1.如图所示,AC=AD,BC=BD,则下列说法正确的是( )
A.AB垂直平分CD; B .CD垂直平分AB ;
C.AB与CD互相垂直平分; D.CD平分∠ ACB .
2.到三角形三个顶点的距离相等的点是( )
A.三条角平分线的交点 B.三边垂直平分线的交点
C.三边高线的交点 D.没有这样的点
A
B
3.如图,已知在△ABC中,DE是BC的垂直平分线,垂足为E,交AC于点D,若AB=6,AC=9,则△ABD的周长是 .
4.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上.若AB=5cm,BC=6cm,则AC= ,DE= .
8cm
15
5cm
A
B
O
E
D
C
证明:
因为OE平分∠AOB,EC⊥OA,ED⊥OB,
所以DE=CE.
∠DOE=∠COE,
因为EC⊥OA,ED⊥OB,所以∠ODE=∠OCE=90°,
所以△OED≌△OEC(AAS),所以OC=OD;
所以 OE是CD的垂直平分线.
5.如图所示,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D,连接CD.求证:OE是CD的垂直平分线.
解:(1)逆命题是全等三角形的三边对应相等,真命题,是互逆定理.
(2)逆命题是三个角对应相等的两个三角形全等,假命题.
(4)逆命题是同旁内角互补,两直线平行,真命题,是互逆定理.
6.写出下列命题的逆命题,并判断其真假,指出其中的互逆定理.
(1)三边对应相等的两个三角形全等;
(2)全等三角形的三个角对应相等;
(3)两直线平行,同旁内角互补.
课堂小结
肆
课堂小结
线段垂直平分线上的点与这条线段两个端点的距离相等.
PA=PB
点P在线段AB的垂直平分线上.
与线段两个端点距离相等的点在这条线段的垂直平分线上.
线段垂直平分线上的点与线段两个端点的距离相等.
与线段两个端点距离相等的点在这条线段的垂直平分线上.
原命题
逆命题
课后作业
基础题:1.课后习题 第 4,5,6题。
提高题:2.请学有余力的同学完成课后习题第13题
谢
谢
同课章节目录
