15.2 画轴对称的图形 第2课时 关于坐标轴对称的点的坐标特征 课件(共29张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 15.2 画轴对称的图形 第2课时 关于坐标轴对称的点的坐标特征 课件(共29张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 22:45:01 | ||
图片预览






文档简介
(共29张PPT)
第15章 轴对称
15.2 画轴对称的图形
第2课时 关于坐标轴对称的点的坐标特征
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
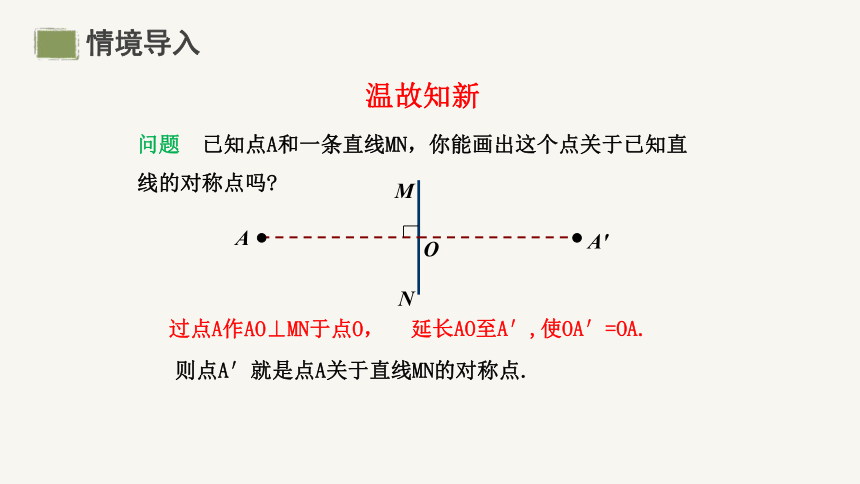
问题 已知点A和一条直线MN,你能画出这个点关于已知直线的对称点吗
A
A′
M
N
则点A′就是点A关于直线MN的对称点.
O
延长AO至A′,使OA′=OA.
过点A作AO⊥MN于点O,
温故知新
平面直角坐标系是数形结合的一个桥梁,如果我们在平面直角坐标系中作轴对称图形,能不能从数量的角度刻画轴对称呢?
思
考
新知初探
贰
新知初探
任务一 探究关于坐标轴对称的点的坐标规律
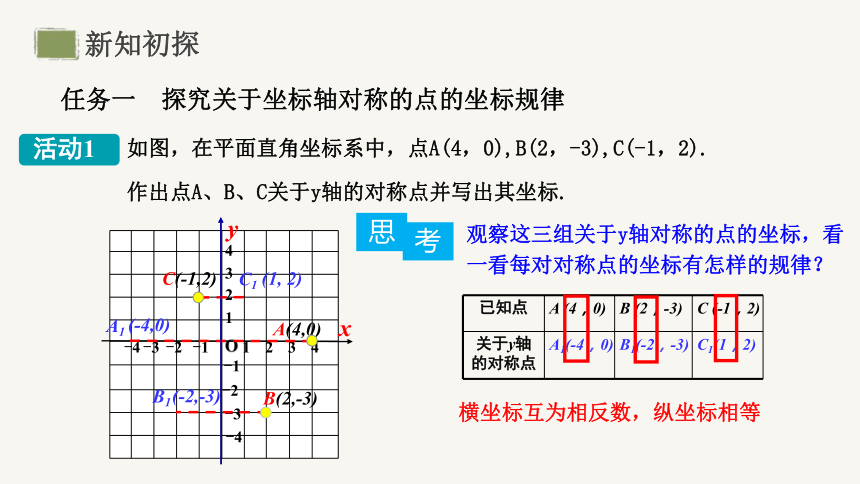
如图,在平面直角坐标系中,点A(4,0),B(2,-3),C(-1,2).
作出点A、B、C关于y轴的对称点并写出其坐标.
1
x
y
2
3
4
1
2
3
4
-1
-2
-3
-4
-4
-3
-2
-1
O
A(4,0)
B(2,-3)
C(-1,2)
A1
B1
C1
已知点 A (4,0) B (2,-3) C (-1,2)
关于y轴的对称点 A1(-4,0) B1(-2,-3) C1(1,2)
观察这三组关于y轴对称的点的坐标,看一看每对对称点的坐标有怎样的规律?
横坐标互为相反数,纵坐标相等
(1, 2)
(-4,0)
(-2,-3)
活动1
思
考
b
a
-a
x
y
O
P(a,b)
P1
( ,b)
-a
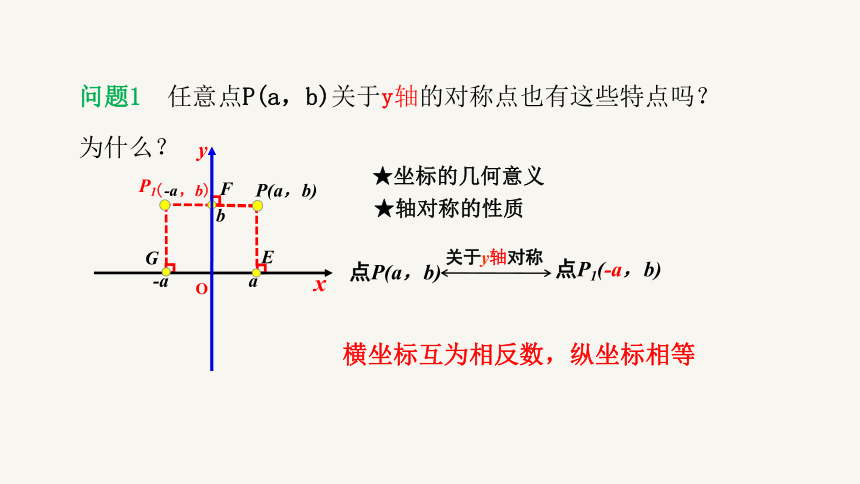
问题1 任意点P(a,b)关于y轴的对称点也有这些特点吗?
为什么?
点P1(-a,b)
点P(a,b)
关于y轴对称
横坐标互为相反数,纵坐标相等
E
F
G
★坐标的几何意义
★轴对称的性质
知识归纳
关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等.
(x , y)
( , )
-x
y
1.点P(-2.5, 6)与点Q关于y轴对称,则点Q的坐标为__________.
2.点M(a, -5)与点N(-2, b)关于y轴对称,则a=_____, b =_____.
即时测评
(2.5 , 6 )
2
-5
(2.5 , )
点P2(a,-b)
关于x轴对称
点P(a,b)
问题2 关于y轴对称的点的坐标是有规律的,那么关于
x轴对称的点的坐标是不是也有规律呢?如果有,你能猜想一下坐标变换的规律吗?
横坐标相等,纵坐标互为相反数
x
y
O
C (3,-4)
C '(3,4)
B(-4,2)
B '(-4,-2)
a
E
b
x
y
O
P(a,b)
P2
(a, )
问题3 如何运用所学知识证明我们的猜想:
关于x轴对称的点的坐标规律为横坐标相等,纵坐标互为相反数?
点P2(a,-b)
关于x轴对称
点P(a,b)
-b
-b
横坐标相等,纵坐标互为相反数
F
G
★坐标的几何意义
★轴对称的性质
知识归纳
关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
(x , y)
( , )
x
-y
即时测评
1.点P(-2.5, 6)与点Q关于x轴对称,则点Q的坐标为__________.
2.点M(a, -5)与点N(-2, b)关于x轴对称,则a=_____, b =_____.
(-2.5 , -6 )
-2
5
(-2.5 , )
P2(-x,y)
●
P(x,y)
●
y
x
O
P1(x,-y)
●
知识归纳
点(x, y)关于x 轴对称的点的坐标为(x,-y)
关于坐标轴对称的点的坐标规律:
点关于直线对称的几何特点用坐标的代数形式来表现出来,体现了我们数学中的数形结合思想方法.
点(x, y)关于y 轴对称的点的坐标为 (-x,y)
解:(1)点(x,y)关于y 轴对称的点的坐标为
(-x,y)因此四边形ABCD 的顶点A,B,C,D
关于y 轴对称的点坐标分别为:
A1( , ), B1( , ),
C1( , ), D1( , ),
范例应用
【例1】 如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),C(-2,5),D(-5,4).
(1)若四边形A1B1C1D1与四边形ABCD关于y轴成轴对称,请写出四边形A1B1C1D1顶点坐标.
(2)作出四边形ABCD关于x轴的轴对称图形.
5 1
2 1
2 5
5 4
依次连接A2B2,B2C2, C2D2, A2D2 ,
A2
解:(2)点(x,y)关于x 轴对称的点的坐标为(x,-y),因此四边形ABCD 的顶点A,B,C,D 关于x 轴对称的点分别为:
A2( , ),B2( , ),
C2( , ),D2( , ),
-2 -5
-5 -1
-2 -1
-5 -4
D2
C2
B2
则四边形A2B2C2D2为所求图形.
【例1】 如图,四边形ABCD的四个顶点的坐标分别
为A(-5,1),B(-2,1),C(-2,5),D(-5,4).
(2)作出四边形ABCD关于x轴的轴对称图形.
依次连接A2B2,B2C2, C2D2, A2D2
A2
方法二:作四边形ABCD 的顶点A,B,C,D 关于x 轴对称的点分别为A2、B2、 C2、 D2,
D2
C2
B2
则四边形A2B2C2D2为所求图形.
【例1】 如图,四边形ABCD的四个顶点的坐标分别
为A(-5,1),B(-2,1),C(-2,5),D(-5,4).
(2)作出四边形ABCD关于x轴的轴对称图形.
(2)四边形ABCD 的顶点A,B,C,D 关于x 轴对称的点分别为:
A2(-5,-1),B2(-2,-1),
C2(-2,-5), D2(-5,-4)
依次连接A2B2,B2C2, C2D2, A2D2
则四边形A2B2C2D2为所求图形.
(2)作四边形ABCD 的顶点A,B,C,D 关于x 轴对称的点分别为A2、B2、 C2、 D2,
依次连接A2B2,B2C2, C2D2, A2D2
则四边形A2B2C2D2为所求图形.
在坐标系中作已知图形关于坐标轴对称图形
精准
快捷
适用范围广
1.找对称点坐标
2.描点
3.连线
归纳总结
范例应用
【例2】 已知点P的坐标为P(a+1,2a-1)
(1)若点P与点A (2a-b,5+a)关于y轴对称,求a、b的值;
(2)若点P关于x轴的对称点在第一象限,求a的取值范围.
解:(1)依题意得
∵点P、A关于y轴对称,
解决给定两个含参坐标的轴对称题可根据关于x轴、y轴对称的点的特征列方程(组)求解.
横坐标互为相反数,纵坐标相等
∴
∴
【例2】已知点P的坐标为P(a+1,2a-1)
(1)若点P与点A (2a-b,5+a)关于y轴对称,求a、b的值;
(2)若点P关于x 轴的对称点P′在第一象限,求a的取值范围.
解:(2)∵P关于x轴对称点的坐标P′(a+1,-2a+1)
P′(a+1,-2a+1)
又∵P关于x轴对称点P′在第一象限
解得
即a的取值范围是
x
y
O
P′
P
一般先写出对称点的坐标或判断已知点所在的象限,再由各象限内点的坐标的符号,列不等式(组)求解.
当堂达标
叁
1.在平面直角坐标系中, 点B的坐标是(4,-1), 点A与点B关于x轴对称,
则点A的坐标是( )
A.(4,1) B.(-1,4) C.(-4,-1) D.(-1,-4)
2.若点A(m,2)与点B(3,n)关于x轴对称, 则m+n的值是( )
A.1 B.-2 C.2 D.5
3. 点_________与点(-2,-3)关于x轴对称;
点(-1,4)与点________关于y轴对称.
4.已知点P(2a+b,-3a)与点P′(8,b+2).
若点P与点P′关于x轴对称,则a=_____, b=_______.
若点P与点P′关于y轴对称,则a=_____ ,b=_______.
当堂达标
A
A
(-2,3)
(1,4)
2
4
6
-20
5.平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,-1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)若△ABC与△A'B'C'关于x轴对称,画出△A'B'C',并写出A'、B'、C'的坐标.
x
y
O
解:如图所示.
6.已知点A(2a+b,5+a),B(2b-1,-a+b).
(1)若点A,B关于x轴对称,求a,b的值;
(2)若点A,B关于y轴对称,求(4a+4b)2026的值.
解:(1)因为点A,B关于x轴对称,
所以 解得
(2)因为点A,B关于y轴对称,
所以 解得
所以(4a+4b)2026=(-7+6)2026=(-1)2026=1.
课堂小结
肆
课堂小结
P2(-x,y)
●
二、在平面直角系中作轴对称图形:
P(x,y)
●
y
x
O
P1(x,-y)
●
找对称点坐标 描点 连线
(x , y)
( , )
x
-y
关于x轴对称
(x , y)
( , )
-x
y
关于y轴对称
把图形的对称问题转化为关键点的对称问题
一、关于坐标轴对称的点的坐标规律:
课后作业
基础题:1.课后习题 第 3,4题。
提高题:2.请学有余力的同学完成课后习题第8题
谢
谢
第15章 轴对称
15.2 画轴对称的图形
第2课时 关于坐标轴对称的点的坐标特征
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
问题 已知点A和一条直线MN,你能画出这个点关于已知直线的对称点吗
A
A′
M
N
则点A′就是点A关于直线MN的对称点.
O
延长AO至A′,使OA′=OA.
过点A作AO⊥MN于点O,
温故知新
平面直角坐标系是数形结合的一个桥梁,如果我们在平面直角坐标系中作轴对称图形,能不能从数量的角度刻画轴对称呢?
思
考
新知初探
贰
新知初探
任务一 探究关于坐标轴对称的点的坐标规律
如图,在平面直角坐标系中,点A(4,0),B(2,-3),C(-1,2).
作出点A、B、C关于y轴的对称点并写出其坐标.
1
x
y
2
3
4
1
2
3
4
-1
-2
-3
-4
-4
-3
-2
-1
O
A(4,0)
B(2,-3)
C(-1,2)
A1
B1
C1
已知点 A (4,0) B (2,-3) C (-1,2)
关于y轴的对称点 A1(-4,0) B1(-2,-3) C1(1,2)
观察这三组关于y轴对称的点的坐标,看一看每对对称点的坐标有怎样的规律?
横坐标互为相反数,纵坐标相等
(1, 2)
(-4,0)
(-2,-3)
活动1
思
考
b
a
-a
x
y
O
P(a,b)
P1
( ,b)
-a
问题1 任意点P(a,b)关于y轴的对称点也有这些特点吗?
为什么?
点P1(-a,b)
点P(a,b)
关于y轴对称
横坐标互为相反数,纵坐标相等
E
F
G
★坐标的几何意义
★轴对称的性质
知识归纳
关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等.
(x , y)
( , )
-x
y
1.点P(-2.5, 6)与点Q关于y轴对称,则点Q的坐标为__________.
2.点M(a, -5)与点N(-2, b)关于y轴对称,则a=_____, b =_____.
即时测评
(2.5 , 6 )
2
-5
(2.5 , )
点P2(a,-b)
关于x轴对称
点P(a,b)
问题2 关于y轴对称的点的坐标是有规律的,那么关于
x轴对称的点的坐标是不是也有规律呢?如果有,你能猜想一下坐标变换的规律吗?
横坐标相等,纵坐标互为相反数
x
y
O
C (3,-4)
C '(3,4)
B(-4,2)
B '(-4,-2)
a
E
b
x
y
O
P(a,b)
P2
(a, )
问题3 如何运用所学知识证明我们的猜想:
关于x轴对称的点的坐标规律为横坐标相等,纵坐标互为相反数?
点P2(a,-b)
关于x轴对称
点P(a,b)
-b
-b
横坐标相等,纵坐标互为相反数
F
G
★坐标的几何意义
★轴对称的性质
知识归纳
关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
(x , y)
( , )
x
-y
即时测评
1.点P(-2.5, 6)与点Q关于x轴对称,则点Q的坐标为__________.
2.点M(a, -5)与点N(-2, b)关于x轴对称,则a=_____, b =_____.
(-2.5 , -6 )
-2
5
(-2.5 , )
P2(-x,y)
●
P(x,y)
●
y
x
O
P1(x,-y)
●
知识归纳
点(x, y)关于x 轴对称的点的坐标为(x,-y)
关于坐标轴对称的点的坐标规律:
点关于直线对称的几何特点用坐标的代数形式来表现出来,体现了我们数学中的数形结合思想方法.
点(x, y)关于y 轴对称的点的坐标为 (-x,y)
解:(1)点(x,y)关于y 轴对称的点的坐标为
(-x,y)因此四边形ABCD 的顶点A,B,C,D
关于y 轴对称的点坐标分别为:
A1( , ), B1( , ),
C1( , ), D1( , ),
范例应用
【例1】 如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),C(-2,5),D(-5,4).
(1)若四边形A1B1C1D1与四边形ABCD关于y轴成轴对称,请写出四边形A1B1C1D1顶点坐标.
(2)作出四边形ABCD关于x轴的轴对称图形.
5 1
2 1
2 5
5 4
依次连接A2B2,B2C2, C2D2, A2D2 ,
A2
解:(2)点(x,y)关于x 轴对称的点的坐标为(x,-y),因此四边形ABCD 的顶点A,B,C,D 关于x 轴对称的点分别为:
A2( , ),B2( , ),
C2( , ),D2( , ),
-2 -5
-5 -1
-2 -1
-5 -4
D2
C2
B2
则四边形A2B2C2D2为所求图形.
【例1】 如图,四边形ABCD的四个顶点的坐标分别
为A(-5,1),B(-2,1),C(-2,5),D(-5,4).
(2)作出四边形ABCD关于x轴的轴对称图形.
依次连接A2B2,B2C2, C2D2, A2D2
A2
方法二:作四边形ABCD 的顶点A,B,C,D 关于x 轴对称的点分别为A2、B2、 C2、 D2,
D2
C2
B2
则四边形A2B2C2D2为所求图形.
【例1】 如图,四边形ABCD的四个顶点的坐标分别
为A(-5,1),B(-2,1),C(-2,5),D(-5,4).
(2)作出四边形ABCD关于x轴的轴对称图形.
(2)四边形ABCD 的顶点A,B,C,D 关于x 轴对称的点分别为:
A2(-5,-1),B2(-2,-1),
C2(-2,-5), D2(-5,-4)
依次连接A2B2,B2C2, C2D2, A2D2
则四边形A2B2C2D2为所求图形.
(2)作四边形ABCD 的顶点A,B,C,D 关于x 轴对称的点分别为A2、B2、 C2、 D2,
依次连接A2B2,B2C2, C2D2, A2D2
则四边形A2B2C2D2为所求图形.
在坐标系中作已知图形关于坐标轴对称图形
精准
快捷
适用范围广
1.找对称点坐标
2.描点
3.连线
归纳总结
范例应用
【例2】 已知点P的坐标为P(a+1,2a-1)
(1)若点P与点A (2a-b,5+a)关于y轴对称,求a、b的值;
(2)若点P关于x轴的对称点在第一象限,求a的取值范围.
解:(1)依题意得
∵点P、A关于y轴对称,
解决给定两个含参坐标的轴对称题可根据关于x轴、y轴对称的点的特征列方程(组)求解.
横坐标互为相反数,纵坐标相等
∴
∴
【例2】已知点P的坐标为P(a+1,2a-1)
(1)若点P与点A (2a-b,5+a)关于y轴对称,求a、b的值;
(2)若点P关于x 轴的对称点P′在第一象限,求a的取值范围.
解:(2)∵P关于x轴对称点的坐标P′(a+1,-2a+1)
P′(a+1,-2a+1)
又∵P关于x轴对称点P′在第一象限
解得
即a的取值范围是
x
y
O
P′
P
一般先写出对称点的坐标或判断已知点所在的象限,再由各象限内点的坐标的符号,列不等式(组)求解.
当堂达标
叁
1.在平面直角坐标系中, 点B的坐标是(4,-1), 点A与点B关于x轴对称,
则点A的坐标是( )
A.(4,1) B.(-1,4) C.(-4,-1) D.(-1,-4)
2.若点A(m,2)与点B(3,n)关于x轴对称, 则m+n的值是( )
A.1 B.-2 C.2 D.5
3. 点_________与点(-2,-3)关于x轴对称;
点(-1,4)与点________关于y轴对称.
4.已知点P(2a+b,-3a)与点P′(8,b+2).
若点P与点P′关于x轴对称,则a=_____, b=_______.
若点P与点P′关于y轴对称,则a=_____ ,b=_______.
当堂达标
A
A
(-2,3)
(1,4)
2
4
6
-20
5.平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,-1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)若△ABC与△A'B'C'关于x轴对称,画出△A'B'C',并写出A'、B'、C'的坐标.
x
y
O
解:如图所示.
6.已知点A(2a+b,5+a),B(2b-1,-a+b).
(1)若点A,B关于x轴对称,求a,b的值;
(2)若点A,B关于y轴对称,求(4a+4b)2026的值.
解:(1)因为点A,B关于x轴对称,
所以 解得
(2)因为点A,B关于y轴对称,
所以 解得
所以(4a+4b)2026=(-7+6)2026=(-1)2026=1.
课堂小结
肆
课堂小结
P2(-x,y)
●
二、在平面直角系中作轴对称图形:
P(x,y)
●
y
x
O
P1(x,-y)
●
找对称点坐标 描点 连线
(x , y)
( , )
x
-y
关于x轴对称
(x , y)
( , )
-x
y
关于y轴对称
把图形的对称问题转化为关键点的对称问题
一、关于坐标轴对称的点的坐标规律:
课后作业
基础题:1.课后习题 第 3,4题。
提高题:2.请学有余力的同学完成课后习题第8题
谢
谢
同课章节目录
