15.3.1 等腰三角形 第1课时 等腰三角形的性质 课件(共30张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 15.3.1 等腰三角形 第1课时 等腰三角形的性质 课件(共30张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 22:45:14 | ||
图片预览








文档简介
(共30张PPT)
第15章 轴对称
15.3 等腰三角形
15.3.1 等腰三角形
第1课时 等腰三角形的性质
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
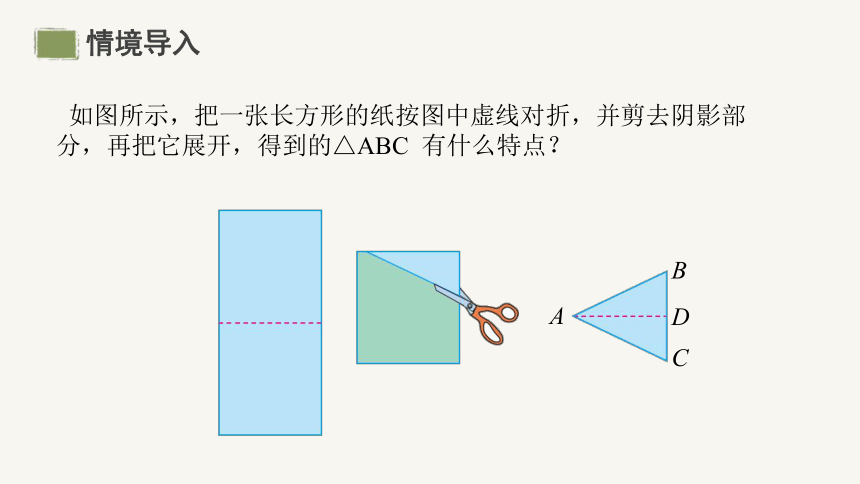
如图所示,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC 有什么特点?
A
B
C
D
新知初探
贰
新知初探
任务一 探究等腰三角形的性质
思
考
(1)怎么样的三角形为等腰三角形?
有两边相等的三角形是等腰三角形.
(2)一般的三角形与等腰三角形在角上有什么不同?等腰三角形特殊在哪里?
等腰三角形的两个底角 .
相等
腰
腰
底边
底角
底角
顶角
活动1
如图,在纸上画一个等腰三角形,把它剪下来.
B
A
C
D
A
B
C
D
问题1 等腰三角形是轴对称图形吗?它有几条对称轴
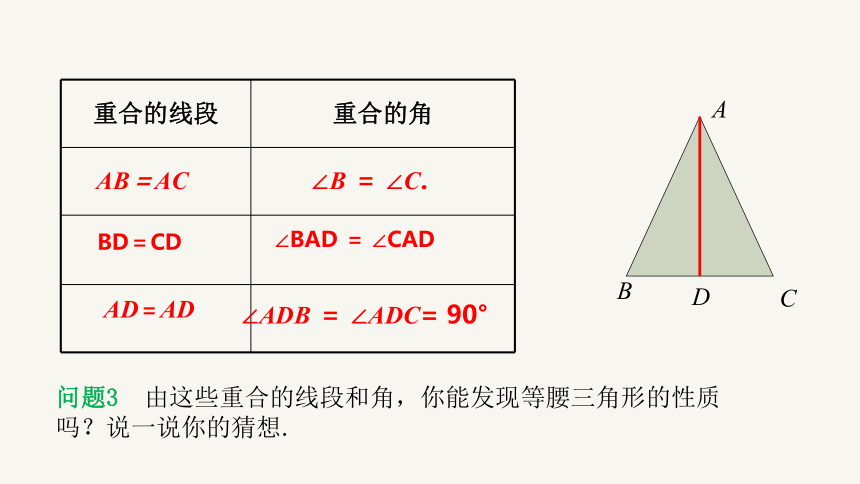
问题2 将这个等腰三角形对折,使它的两腰重合,再展开,找出其中重合的线段与角.
是轴对称图形,1条对称轴
重合的线段 重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC= 90°
问题3 由这些重合的线段和角,你能发现等腰三角形的性质吗?说一说你的猜想.
猜想:
(1)等腰三角形的两个底角相等.
(2)等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合.
如何证明这个结论呢?
问题4 怎么证明命题“等腰三角形的两个底角相等”?
命题的题设是什么?结论是什么?你能画图,写出已知、求证吗?
等腰三角形的两个底角相等
(题设)
如果一个三角形是等腰三角形,
那么这个三角形的两个底角相等.
(结论)
构造(添加辅助线)
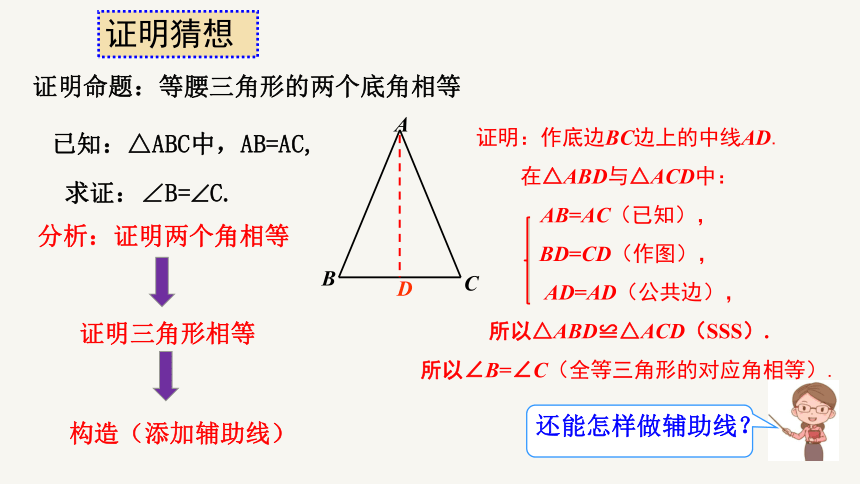
证明命题:等腰三角形的两个底角相等
证明猜想
已知:△ABC中,AB=AC,
求证:∠B= C.
分析:证明两个角相等
证明三角形相等
还能怎样做辅助线?
A
B
C
D
证明:作底边BC边上的中线AD.
在△ABD与△ACD中:
AB=AC(已知),
BD=CD(作图),
AD=AD(公共边),
所以△ABD≌△ACD(SSS).
所以∠B=∠C(全等三角形的对应角相等).
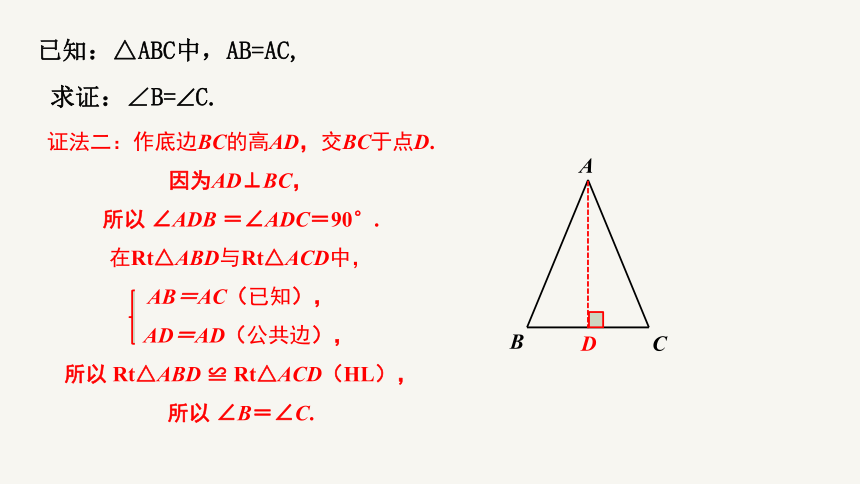
已知:△ABC中,AB=AC,
求证:∠B= C.
证法二:作底边BC的高AD,交BC于点D.
因为AD⊥BC,
所以 ∠ADB =∠ADC=90°.
在Rt△ABD与Rt△ACD中,
AB=AC(已知),
AD=AD(公共边),
所以 Rt△ABD ≌ Rt△ACD(HL),
所以 ∠B=∠C.
A
B
C
D
已知:△ABC中,AB=AC,
求证:∠B= C.
证法三:作顶角∠BAC的平分线AD,交BC于点D.
因为AD平分∠BAC ,
所以∠1=∠2.
在△ABD与△ACD中,
AB=AC(已知),
∠1=∠2(已证),
AD=AD(公共边),
所以 △ABD ≌ △ACD(SAS),
所以 ∠B=∠C.
A
B
C
D
(
(
1
2
等腰三角形的性质1:
等腰三角形的两个底角相等(简写成“等边对等角”)
符号语言:
∵
归纳总结
证法一:作底边BC边上的中线AD.
在△ABD与△ACD中:
AB=AC(已知),
BD=CD(作图),
AD=AD(公共边),
所以△ABD≌△ACD(SSS).
所以∠B= ∠C,
∠BAD=∠CAD,
∠ADB= ∠ADC,
因为∠ADB+ ∠ADC=180 °,
所以∠ADB= ∠ADC=90 °.
(AD是底边上的高)
等腰三角形的性质2:
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.(简写成“三线合一”)
问题5 证明性质1时得到∠B=∠C,
还可以得到其他数学结论吗?
A
B
C
D
(AD是顶角的平分线)
等腰三角形性质2: 等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合,简写成“三线合一”.
“三线合一”的意思是只要产生了其中一条线,那么它同时也是其余的 两条特殊线,具备其余两条线的性质.
符号语言:
或
你还能写出其它的符号语言吗?
性质2: 等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合,简写成“三线合一”.
一般三角形
三线不合一
底角平分线、
腰上的中线、
腰上的高
三线不合一
顶角平分线、
底边上的中线、
底边上的高
三线合一
范例应用
A
B
C
D
【例1】 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
分析:(1)指出图中有几个等腰三角形?
图中有哪些相等的角?
∠A=∠ABD,
∠C=∠BDC=∠ABC;
△ABC,
△ABD,
△BCD.
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
(2)∠BDC与∠A、∠ABD有什么关系,∠ABC、∠C呢?
∠BDC= ∠A+ ∠ABD=2 ∠A=2 ∠ABD,
∠ABC= ∠BDC=2 ∠A,
∠C= ∠BDC=2 ∠A.
(3)图中没有出现任何一个具体的度数,我们应如何求度数?
设∠A=x ,
∵ ∠A+ ∠ABC+ ∠C=180 °,
∴ x+2x+2x=180 °.
设未知数,列方程
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC=∠C=∠BDC=2x.
于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180 ° .
解得x=36 ° .
∴在△ABC中,∠A=36°,∠ABC=∠C=72°.
x
⌒
2x
⌒
2x
⌒
⌒
2x
方法点拨
在含多个等腰三角形的图形中求角时,常常利用方程思想,通过内角、外角之间的关系进行转化求解.
当堂达标
叁
当堂达标
(1)等腰三角形的顶角一定是锐角.
(2)等腰三角形的底角可能是锐角或者直角、钝角都可以.
(3)钝角三角形不可能是等腰三角形.
(4)等腰三角形的顶角平分线一定垂直底边.
(5)等腰三角形的角平分线、中线和高互相重合.
(6)等腰三角形底边上的中线一定平分顶角.
(X)
(X)
(X)
(X)
(√)
1.判断正误
(√)
2.等腰△ABC中,AB=AC,∠A=30°,则∠B=( )
A.30° B.60° C.75° D.85°
3.等腰三角形的一个外角是100°,它的顶角的度数是( )
A.80°B.20°C.20°或80° D.50°或80°
5.如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于( )
A.10 B.5
C.4 D.3
5.如图,在△ABC中,已知AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为( )
A.35° B.45°
C.55° D.60°
B
C
C
C
6.如图所示,在△ABC中,AB=AD=DC,∠BAD=26°,
求∠B和∠C的度数.
D
B
A
C
解:因为∠BAD=26°,AB=AD,
所以∠B=∠ADB= ×(180°-26°)=77°.
因为AD=CD,所以∠C=∠DAC.
因为∠ADB=∠C+∠DAC=2∠C,
所以∠C= ∠ADB=38.5°.
课堂小结
肆
课堂小结
1.等腰三角形性质:
性质1 等腰三角形的两个底角相等(简写成“等边对等角”).
性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合 .简写成“三线合一”.
2.为什么研究等腰三角形?如何研究等腰三角形?
一般三角形
边的大小特殊化
等腰三角形
直角三角形
(角特殊化)
一般几何图形的研究思路
边的大小特殊化
等边三角形
边的位置特殊化
定义
性质
判定
课后作业
基础题:1.课后习题 第 1,3题。
提高题:2.请学有余力的同学完成课后习题第8题
谢
谢
第15章 轴对称
15.3 等腰三角形
15.3.1 等腰三角形
第1课时 等腰三角形的性质
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
如图所示,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC 有什么特点?
A
B
C
D
新知初探
贰
新知初探
任务一 探究等腰三角形的性质
思
考
(1)怎么样的三角形为等腰三角形?
有两边相等的三角形是等腰三角形.
(2)一般的三角形与等腰三角形在角上有什么不同?等腰三角形特殊在哪里?
等腰三角形的两个底角 .
相等
腰
腰
底边
底角
底角
顶角
活动1
如图,在纸上画一个等腰三角形,把它剪下来.
B
A
C
D
A
B
C
D
问题1 等腰三角形是轴对称图形吗?它有几条对称轴
问题2 将这个等腰三角形对折,使它的两腰重合,再展开,找出其中重合的线段与角.
是轴对称图形,1条对称轴
重合的线段 重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC= 90°
问题3 由这些重合的线段和角,你能发现等腰三角形的性质吗?说一说你的猜想.
猜想:
(1)等腰三角形的两个底角相等.
(2)等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合.
如何证明这个结论呢?
问题4 怎么证明命题“等腰三角形的两个底角相等”?
命题的题设是什么?结论是什么?你能画图,写出已知、求证吗?
等腰三角形的两个底角相等
(题设)
如果一个三角形是等腰三角形,
那么这个三角形的两个底角相等.
(结论)
构造(添加辅助线)
证明命题:等腰三角形的两个底角相等
证明猜想
已知:△ABC中,AB=AC,
求证:∠B= C.
分析:证明两个角相等
证明三角形相等
还能怎样做辅助线?
A
B
C
D
证明:作底边BC边上的中线AD.
在△ABD与△ACD中:
AB=AC(已知),
BD=CD(作图),
AD=AD(公共边),
所以△ABD≌△ACD(SSS).
所以∠B=∠C(全等三角形的对应角相等).
已知:△ABC中,AB=AC,
求证:∠B= C.
证法二:作底边BC的高AD,交BC于点D.
因为AD⊥BC,
所以 ∠ADB =∠ADC=90°.
在Rt△ABD与Rt△ACD中,
AB=AC(已知),
AD=AD(公共边),
所以 Rt△ABD ≌ Rt△ACD(HL),
所以 ∠B=∠C.
A
B
C
D
已知:△ABC中,AB=AC,
求证:∠B= C.
证法三:作顶角∠BAC的平分线AD,交BC于点D.
因为AD平分∠BAC ,
所以∠1=∠2.
在△ABD与△ACD中,
AB=AC(已知),
∠1=∠2(已证),
AD=AD(公共边),
所以 △ABD ≌ △ACD(SAS),
所以 ∠B=∠C.
A
B
C
D
(
(
1
2
等腰三角形的性质1:
等腰三角形的两个底角相等(简写成“等边对等角”)
符号语言:
∵
归纳总结
证法一:作底边BC边上的中线AD.
在△ABD与△ACD中:
AB=AC(已知),
BD=CD(作图),
AD=AD(公共边),
所以△ABD≌△ACD(SSS).
所以∠B= ∠C,
∠BAD=∠CAD,
∠ADB= ∠ADC,
因为∠ADB+ ∠ADC=180 °,
所以∠ADB= ∠ADC=90 °.
(AD是底边上的高)
等腰三角形的性质2:
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.(简写成“三线合一”)
问题5 证明性质1时得到∠B=∠C,
还可以得到其他数学结论吗?
A
B
C
D
(AD是顶角的平分线)
等腰三角形性质2: 等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合,简写成“三线合一”.
“三线合一”的意思是只要产生了其中一条线,那么它同时也是其余的 两条特殊线,具备其余两条线的性质.
符号语言:
或
你还能写出其它的符号语言吗?
性质2: 等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合,简写成“三线合一”.
一般三角形
三线不合一
底角平分线、
腰上的中线、
腰上的高
三线不合一
顶角平分线、
底边上的中线、
底边上的高
三线合一
范例应用
A
B
C
D
【例1】 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
分析:(1)指出图中有几个等腰三角形?
图中有哪些相等的角?
∠A=∠ABD,
∠C=∠BDC=∠ABC;
△ABC,
△ABD,
△BCD.
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
(2)∠BDC与∠A、∠ABD有什么关系,∠ABC、∠C呢?
∠BDC= ∠A+ ∠ABD=2 ∠A=2 ∠ABD,
∠ABC= ∠BDC=2 ∠A,
∠C= ∠BDC=2 ∠A.
(3)图中没有出现任何一个具体的度数,我们应如何求度数?
设∠A=x ,
∵ ∠A+ ∠ABC+ ∠C=180 °,
∴ x+2x+2x=180 °.
设未知数,列方程
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC=∠C=∠BDC=2x.
于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180 ° .
解得x=36 ° .
∴在△ABC中,∠A=36°,∠ABC=∠C=72°.
x
⌒
2x
⌒
2x
⌒
⌒
2x
方法点拨
在含多个等腰三角形的图形中求角时,常常利用方程思想,通过内角、外角之间的关系进行转化求解.
当堂达标
叁
当堂达标
(1)等腰三角形的顶角一定是锐角.
(2)等腰三角形的底角可能是锐角或者直角、钝角都可以.
(3)钝角三角形不可能是等腰三角形.
(4)等腰三角形的顶角平分线一定垂直底边.
(5)等腰三角形的角平分线、中线和高互相重合.
(6)等腰三角形底边上的中线一定平分顶角.
(X)
(X)
(X)
(X)
(√)
1.判断正误
(√)
2.等腰△ABC中,AB=AC,∠A=30°,则∠B=( )
A.30° B.60° C.75° D.85°
3.等腰三角形的一个外角是100°,它的顶角的度数是( )
A.80°B.20°C.20°或80° D.50°或80°
5.如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于( )
A.10 B.5
C.4 D.3
5.如图,在△ABC中,已知AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为( )
A.35° B.45°
C.55° D.60°
B
C
C
C
6.如图所示,在△ABC中,AB=AD=DC,∠BAD=26°,
求∠B和∠C的度数.
D
B
A
C
解:因为∠BAD=26°,AB=AD,
所以∠B=∠ADB= ×(180°-26°)=77°.
因为AD=CD,所以∠C=∠DAC.
因为∠ADB=∠C+∠DAC=2∠C,
所以∠C= ∠ADB=38.5°.
课堂小结
肆
课堂小结
1.等腰三角形性质:
性质1 等腰三角形的两个底角相等(简写成“等边对等角”).
性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合 .简写成“三线合一”.
2.为什么研究等腰三角形?如何研究等腰三角形?
一般三角形
边的大小特殊化
等腰三角形
直角三角形
(角特殊化)
一般几何图形的研究思路
边的大小特殊化
等边三角形
边的位置特殊化
定义
性质
判定
课后作业
基础题:1.课后习题 第 1,3题。
提高题:2.请学有余力的同学完成课后习题第8题
谢
谢
同课章节目录
