15.3.2 等边三角形 第2课时 含30°角的直角三角形的性质 课件(共25张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 15.3.2 等边三角形 第2课时 含30°角的直角三角形的性质 课件(共25张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 22:46:03 | ||
图片预览





文档简介
(共25张PPT)
第15章 轴对称
15.3.2 等边三角形
第2课时 含30°角的直角三角形的性质
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
复习旧知
1. 等边三角形的性质:
等边三角形的三个内角都相等,并且每一个角都等于60°.
2. 等边三角形的判定:
(1)三个角都相等的三角形是等边三角形;
(2)有一个角是60°的等腰三角形是等边三角形.
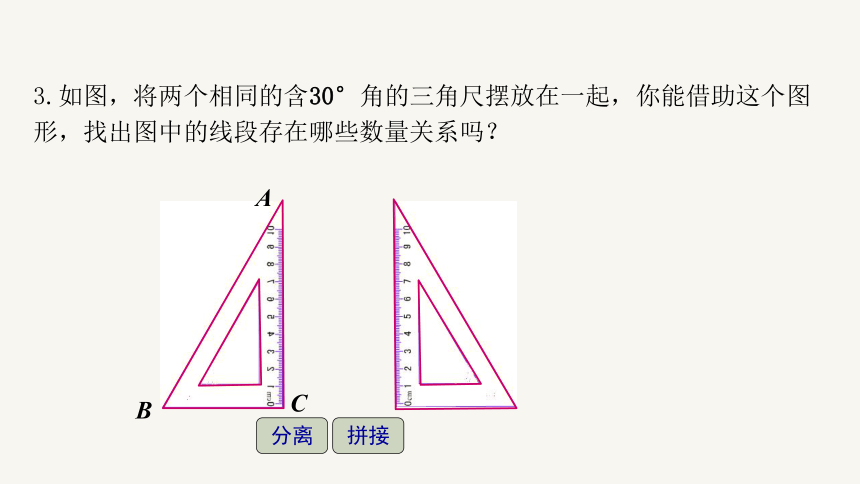
3.如图,将两个相同的含30°角的三角尺摆放在一起,你能借助这个图形,找出图中的线段存在哪些数量关系吗?
分离
拼接
A
C
B
新知初探
贰
新知初探
任务一 含30°角的直角三角形的性质
活动1
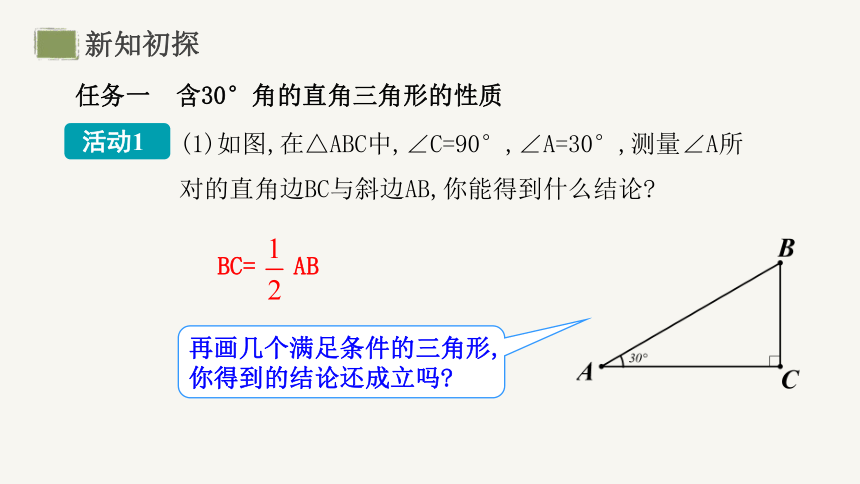
(1)如图,在△ABC中,∠C=90°,∠A=30°,测量∠A所对的直角边BC与斜边AB,你能得到什么结论
BC= AB
再画几个满足条件的三角形,你得到的结论还成立吗
证明猜想
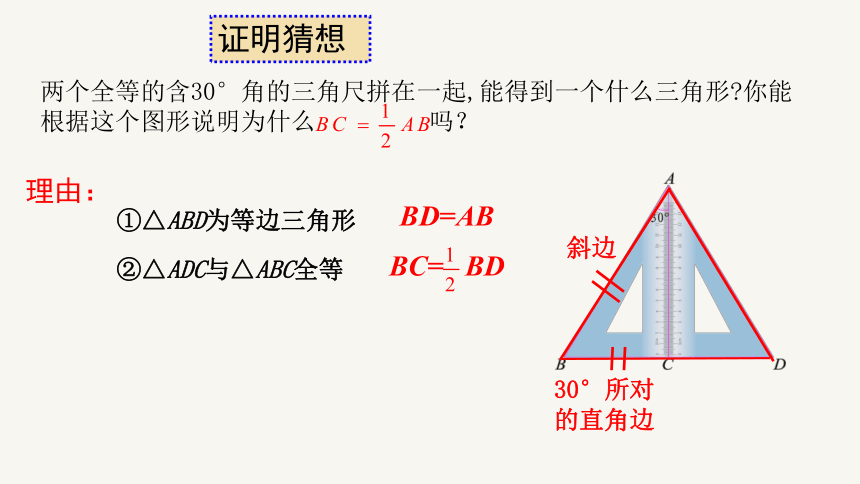
两个全等的含30°角的三角尺拼在一起,能得到一个什么三角形 你能根据这个图形说明为什么 吗?
理由:
①△ABD为等边三角形
②△ADC与△ABC全等
BD=AB
斜边
30°所对
的直角边
BC= BD
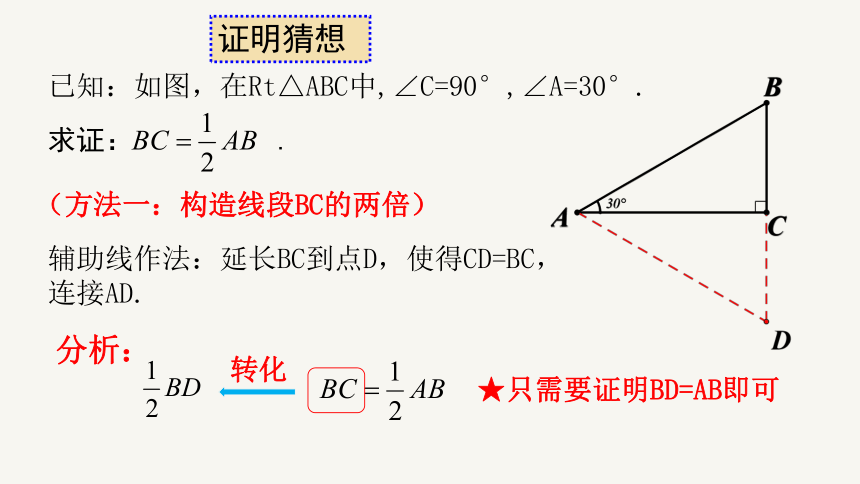
已知:如图,在Rt△ABC中,∠C=90°,∠A=30°.
(方法一:构造线段BC的两倍)
辅助线作法:延长BC到点D,使得CD=BC,连接AD.
求证: .
转化
分析:
★只需要证明BD=AB即可
证明猜想
证明过程
证明:如图,延长BC到点D,使得CD=BC,连接AD,
证明方法:倍长法
暂时不能证明
(方法二:构造线段AB的一半)
D
辅助法的作法:作AB的中点D,连结CD,
★只需要证明BC=BD即可
已知:如图,在Rt△ABC中,∠C=90°,∠A=30°.
求证: .
分析:
转化
你还有其它的证明思路吗?
证明猜想
证明方法:截半法
(换一种思路:在线段AB上截取BD=BC,连结CD)
分析:
已知:如图,在Rt△ABC中,∠C=90°,∠A=30°.
求证: .
转化
★只需要证明点D为AB的中点即可
证明猜想
证明过程
证明:如图,在线段AB上截取BD=BC,连结CD,
证明方法:截半法
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
符号语言:
若 Rt△ABC中,∠C=90°,∠A=30°
则BC= AB(或AB=2BC).
含30°角的直角三角形的性质
知识要点
即时测评
√
判断下列说法是否正确:
1)直角三角形中30°角所对的直角边等于另一直角边的一半.
2)三角形中30°角所对的边等于最长边的一半。
3)直角三角形中较短的直角边是斜边的一半。
4)直角三角形的斜边是30°角所对直角边的2倍.
范例应用
【例题】如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,AB=7.4m,∠A=30°,立柱BC,DE要多长?
分析:要求BC,DE的长度必须要找准这两条线段落在那两个直角三角形中,
求BC
Rt△ABC
求DE
Rt△ADE
解题过程
答:立柱BC的长是3.7m,DE的长是1.85m.
当堂达标
叁
当堂达标
1. 如图所示,在△ABC中,AB=AC,∠B=30°,AB⊥AD,AD=3cm,则BC的长为( )
A.5cm B.9cm C.6cm D.12cm
2.如图,在△ABC中,∠BAC=90°,∠B=30°,AC=5cm,AD⊥BC于D,则BD=( )
A.10cm B.7.5cm C.8.5cm D.6.5cm
3.如图,在等腰三角形ABC中,AB=AC=12 cm,∠BAC=120°,那么中线AD= cm.
B
B
6
4.已知:如图,∠C=90°, ∠B=30°,AD是∠BAC的平分线.
求证:BD=2CD.
证明:∵∠C=90°, ∠B=30°,
∴∠BAC=60°,
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD=30°,
∴∠B=∠BAD,
∴BD=AD,
在Rt△ACD中,∠CAD=30°,
∴AD=2CD,
∴BD=2CD.
5.在△ABC中 ,AB=AC,∠BAC=120° ,D是BC的中点,DE⊥AB于E点,求证:BE=3EA.
证明:∵AB=AC,∠BAC=120°, ∴∠B=∠C=30°.
∵ D是BC的中点,∴AD⊥BC
∴∠ADC=90°,∠BAD=∠DAC=60°.
∴AB=2AD.
∵DE⊥AB,∴∠AED=90°,
∴∠ADE=30°,∴AD=2AE.
∴AB=4AE,∴BE=3AE.
课堂小结
肆
课堂小结
内容
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半
使用要点
含30°角的直角三角形的性质
找准30 °的角所对的直角边,点明斜边
注意
前提条件:直角三角形中
课后作业
基础题:1.课后习题 第 6,7题。
提高题:2.请学有余力的同学完成课后习题第15题
谢
谢
第15章 轴对称
15.3.2 等边三角形
第2课时 含30°角的直角三角形的性质
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
复习旧知
1. 等边三角形的性质:
等边三角形的三个内角都相等,并且每一个角都等于60°.
2. 等边三角形的判定:
(1)三个角都相等的三角形是等边三角形;
(2)有一个角是60°的等腰三角形是等边三角形.
3.如图,将两个相同的含30°角的三角尺摆放在一起,你能借助这个图形,找出图中的线段存在哪些数量关系吗?
分离
拼接
A
C
B
新知初探
贰
新知初探
任务一 含30°角的直角三角形的性质
活动1
(1)如图,在△ABC中,∠C=90°,∠A=30°,测量∠A所对的直角边BC与斜边AB,你能得到什么结论
BC= AB
再画几个满足条件的三角形,你得到的结论还成立吗
证明猜想
两个全等的含30°角的三角尺拼在一起,能得到一个什么三角形 你能根据这个图形说明为什么 吗?
理由:
①△ABD为等边三角形
②△ADC与△ABC全等
BD=AB
斜边
30°所对
的直角边
BC= BD
已知:如图,在Rt△ABC中,∠C=90°,∠A=30°.
(方法一:构造线段BC的两倍)
辅助线作法:延长BC到点D,使得CD=BC,连接AD.
求证: .
转化
分析:
★只需要证明BD=AB即可
证明猜想
证明过程
证明:如图,延长BC到点D,使得CD=BC,连接AD,
证明方法:倍长法
暂时不能证明
(方法二:构造线段AB的一半)
D
辅助法的作法:作AB的中点D,连结CD,
★只需要证明BC=BD即可
已知:如图,在Rt△ABC中,∠C=90°,∠A=30°.
求证: .
分析:
转化
你还有其它的证明思路吗?
证明猜想
证明方法:截半法
(换一种思路:在线段AB上截取BD=BC,连结CD)
分析:
已知:如图,在Rt△ABC中,∠C=90°,∠A=30°.
求证: .
转化
★只需要证明点D为AB的中点即可
证明猜想
证明过程
证明:如图,在线段AB上截取BD=BC,连结CD,
证明方法:截半法
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
符号语言:
若 Rt△ABC中,∠C=90°,∠A=30°
则BC= AB(或AB=2BC).
含30°角的直角三角形的性质
知识要点
即时测评
√
判断下列说法是否正确:
1)直角三角形中30°角所对的直角边等于另一直角边的一半.
2)三角形中30°角所对的边等于最长边的一半。
3)直角三角形中较短的直角边是斜边的一半。
4)直角三角形的斜边是30°角所对直角边的2倍.
范例应用
【例题】如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,AB=7.4m,∠A=30°,立柱BC,DE要多长?
分析:要求BC,DE的长度必须要找准这两条线段落在那两个直角三角形中,
求BC
Rt△ABC
求DE
Rt△ADE
解题过程
答:立柱BC的长是3.7m,DE的长是1.85m.
当堂达标
叁
当堂达标
1. 如图所示,在△ABC中,AB=AC,∠B=30°,AB⊥AD,AD=3cm,则BC的长为( )
A.5cm B.9cm C.6cm D.12cm
2.如图,在△ABC中,∠BAC=90°,∠B=30°,AC=5cm,AD⊥BC于D,则BD=( )
A.10cm B.7.5cm C.8.5cm D.6.5cm
3.如图,在等腰三角形ABC中,AB=AC=12 cm,∠BAC=120°,那么中线AD= cm.
B
B
6
4.已知:如图,∠C=90°, ∠B=30°,AD是∠BAC的平分线.
求证:BD=2CD.
证明:∵∠C=90°, ∠B=30°,
∴∠BAC=60°,
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD=30°,
∴∠B=∠BAD,
∴BD=AD,
在Rt△ACD中,∠CAD=30°,
∴AD=2CD,
∴BD=2CD.
5.在△ABC中 ,AB=AC,∠BAC=120° ,D是BC的中点,DE⊥AB于E点,求证:BE=3EA.
证明:∵AB=AC,∠BAC=120°, ∴∠B=∠C=30°.
∵ D是BC的中点,∴AD⊥BC
∴∠ADC=90°,∠BAD=∠DAC=60°.
∴AB=2AD.
∵DE⊥AB,∴∠AED=90°,
∴∠ADE=30°,∴AD=2AE.
∴AB=4AE,∴BE=3AE.
课堂小结
肆
课堂小结
内容
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半
使用要点
含30°角的直角三角形的性质
找准30 °的角所对的直角边,点明斜边
注意
前提条件:直角三角形中
课后作业
基础题:1.课后习题 第 6,7题。
提高题:2.请学有余力的同学完成课后习题第15题
谢
谢
同课章节目录
