16.2 整式的乘法 第2课时 单项式乘多项式 课件(共25张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 16.2 整式的乘法 第2课时 单项式乘多项式 课件(共25张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1000.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 22:51:02 | ||
图片预览





文档简介
(共25张PPT)
第16章 整式的乘法
16.2 整式的乘法
第2课时 单项式乘多项式
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
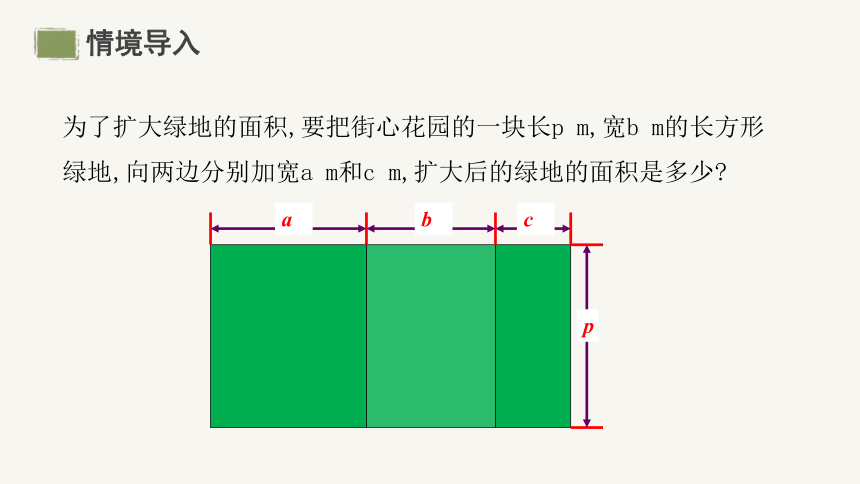
为了扩大绿地的面积,要把街心花园的一块长p m,宽b m的长方形绿地,向两边分别加宽a m和c m,扩大后的绿地的面积是多少
c
b
a
p
新知初探
贰
新知初探
任务一 探究单项式与多项式的运算法则
活动1
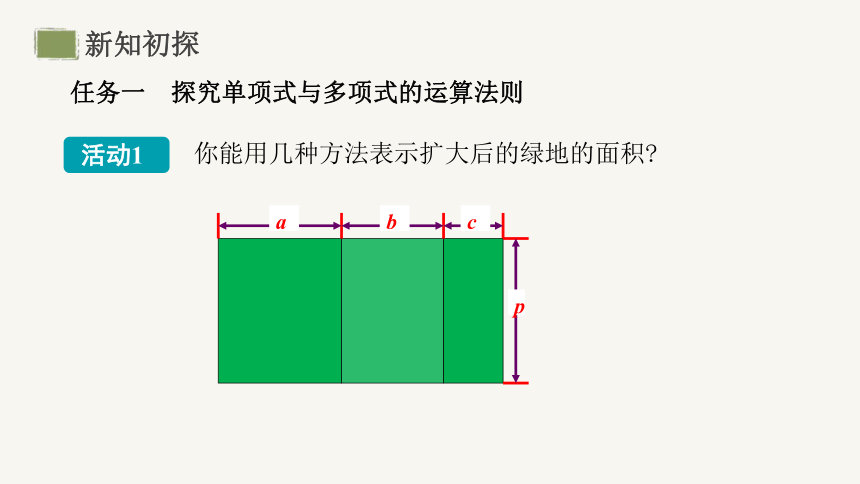
你能用几种方法表示扩大后的绿地的面积
c
b
a
p
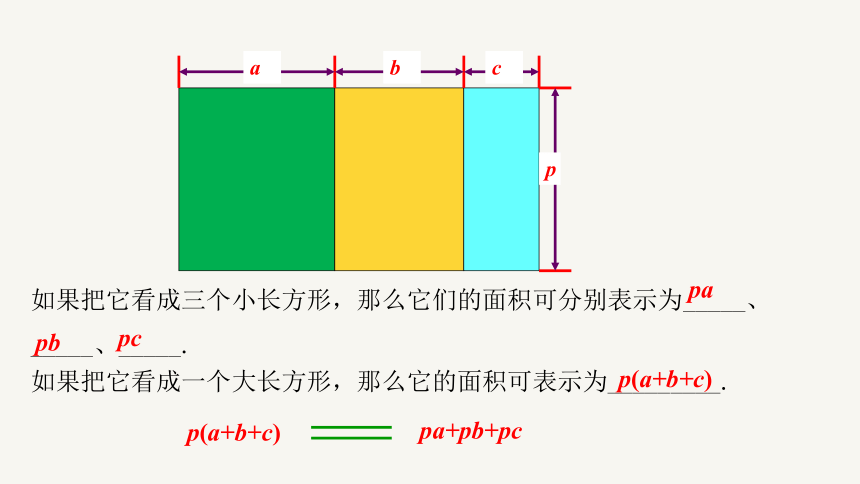
如果把它看成三个小长方形,那么它们的面积可分别表示为_____、_____、_____.
如果把它看成一个大长方形,那么它的面积可表示为_________.
c
b
a
p
pa
pc
pb
p(a+b+c)
pa+pb+pc
p(a+b+c)
pa+pb+pc
p(a+b+c)
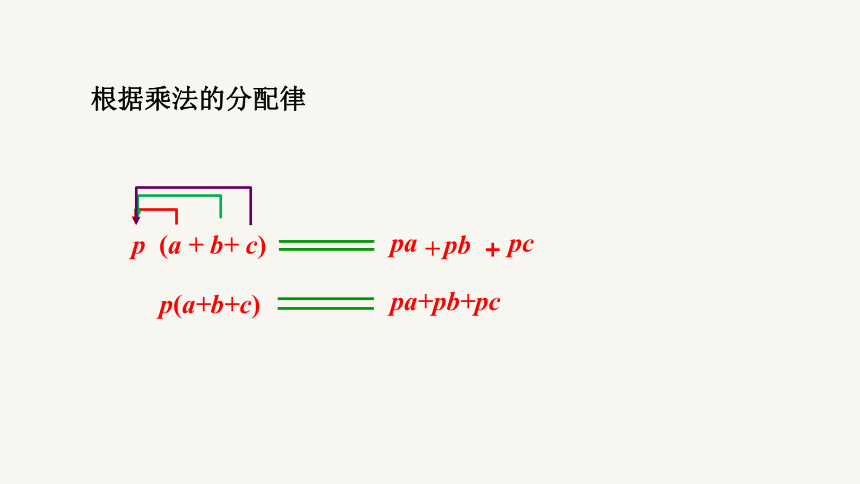
p (a + b+ c)
pb
+
pa
+
根据乘法的分配律
pc
知识要点
单项式乘以多项式的法则
一般地,单项式与多项式相乘,就是用单项式乘多项式的每一项,再把所得的积相加.
(1)依据是乘法分配律
(2)积的项数与多项式的项数相同.
注意
范例应用
例1 计算:
(1)(-4x)·(2x2+3x-1);
解:(1)(-4x)·(2x2+3x-1)
=
=-8x3-12x2+4x;
(-4x)·(2x2)
(-4x)·3x
(-4x)·(-1)
+
+
(2)原式
(2)
例1 计算:
(3)(x-3y)(xy2)2; (4)x(y-z)-y(z-x)+z(x-y).
解:(3)(x-3y)(xy2)2
=(x-3y) (x2y4)
=x x2y4+(-3y) x2y4
=x3y4-3x2y3.
(4)x(y-z)-y(z-x)+z(x-y)
=xy+x(-z)+(-y)z+(-y)(-x)+zx+z(-y)
=xy-xz-yz+xy+xz-yz
=2xy-2yz.
单项式与多项式相乘
单项式与单项式相乘
乘法分配律
转化
即时测评
①
②
③
下列各题的解法是否正确,如果错了,指出错在什么地方,并改正过来.
×
×
×
漏了单独字母
漏乘1
符号没有变化
例2 先化简,再求值:3a(2a2-4a+3)-2a2(3a+4), 其中a=-2.
当a=-2时,
解:3a(2a2-4a+3)-2a2(3a+4)
=6a3-12a2+9a-6a3-8a2
=-20a2+9a.
原式=-20×4-9×2=-98.
方法总结:在做乘法计算时,一定要注意单项式的符号和多项式中每一项的符号,不要搞错.
即时测评
先化简,再求值:x(x2-6x-9)-x(x2-8x-15)+2x(3-x),其中x=- .
解:x(x2-6x-9)-x(x2-8x-15)+2x(3-x)
=x3-6x2-9x-x3+8x2+15x+6x-2x2
=12x.
把x=- 代入得:原式=12x=12×(- )=-2.
例3 如果(-3x)2(x2-2nx+2)的展开式中不含x3项,求n的值.
方法总结:在整式乘法的混合运算中,要注意运算顺序.注意当要求多项式中不含有哪一项时,则表示这一项的系数为0.
解:(-3x)2(x2-2nx+2)
=9x2(x2-2nx+2)
=9x4-18nx3+18x2.
∵展开式中不含x3项,∴n=0.
单项式乘多项式的“两注意”
(1)乘积中每项的符号的确定:在确定积的每一项的符号时,
既要看多项式中每一项的符号,又要看单项式的符号,才能
正确确定积的每一项的符号.
(2)乘积的项数:非零单项式乘多项式,乘积仍是多项式,积
的项数与所乘多项式的项数相同.
归纳总结
当堂达标
叁
1. 下列计算正确的是( )
(A)-a(-a+b)=a2+ab
(B)x(-3x2+x-1)=-3x3+x2-1
(C)5m-2m(m-1)=3m2-3m
(D)(y-2y2+1)(-3y)=6y3-3y2-3y
2.如果ax(3x-4x2y+by2)=6x2-8x3y+6xy2成立,则( )
(A)a=3,b=2 (B)a=2,b=3 (C)a=-3,b=2 (D)a=-2,b=3
3.已知x2-2=y,则2x(x-3y)+2y(3x-1)-2是 .
当堂达标
B
D
2
(1) 4(a - b + 1) = ____________;
4a - 4b + 4
(2) 3x(2x - y2) = __________;
6x2 - 3xy2
(3) (2x - 5y + 6z)(-3x) = ________________;
-6x2 + 15xy - 18xz
(4) (-2a2)2(-a - 2b + c) = _________________.
-4a5 - 8a4b + 4a4c
4. 计算:
5. 计算:-2x2·(xy + y2)-5x(x2y-xy2).
解:原式 = (-2x2)·xy + (-2x2)·y2 + (-5x)·x2y + (-5x)·(-xy2)
= -2x3y + (-2x2y2) + (-5x3y) + 5x2y2
= -7x3y + 3x2y2.
6. 解方程:8x(5-x) = 34-2x(4x-3).
解得 x = 1.
解:去括号,得 40x-8x2 = 34-8x2 + 6x.
移项,得 40x-6x = 34.
合并同类项,得 34x = 34.
住宅用地
人民广场
商业用地
3a
3a + 2b
2a - b
4a
7. 如图,一块长方形地用来建造住宅、广场、商厦,
求这块地的总面积.
解:4a [(3a + 2b) + (2a-b)]
= 4a (5a + b)
= 4a · 5a + 4a · b
= 20a2 + 4ab.
答:这块地的总面积为
(20a2 + 4ab).
课堂小结
肆
课堂小结
单项式乘以多项式
转化
运用乘法分配律
单项式乘以单项式
课后作业
基础题:1.课后习题 第 2题。
提高题:2.请学有余力的同学完成课后习题第9题
谢
谢
第16章 整式的乘法
16.2 整式的乘法
第2课时 单项式乘多项式
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
为了扩大绿地的面积,要把街心花园的一块长p m,宽b m的长方形绿地,向两边分别加宽a m和c m,扩大后的绿地的面积是多少
c
b
a
p
新知初探
贰
新知初探
任务一 探究单项式与多项式的运算法则
活动1
你能用几种方法表示扩大后的绿地的面积
c
b
a
p
如果把它看成三个小长方形,那么它们的面积可分别表示为_____、_____、_____.
如果把它看成一个大长方形,那么它的面积可表示为_________.
c
b
a
p
pa
pc
pb
p(a+b+c)
pa+pb+pc
p(a+b+c)
pa+pb+pc
p(a+b+c)
p (a + b+ c)
pb
+
pa
+
根据乘法的分配律
pc
知识要点
单项式乘以多项式的法则
一般地,单项式与多项式相乘,就是用单项式乘多项式的每一项,再把所得的积相加.
(1)依据是乘法分配律
(2)积的项数与多项式的项数相同.
注意
范例应用
例1 计算:
(1)(-4x)·(2x2+3x-1);
解:(1)(-4x)·(2x2+3x-1)
=
=-8x3-12x2+4x;
(-4x)·(2x2)
(-4x)·3x
(-4x)·(-1)
+
+
(2)原式
(2)
例1 计算:
(3)(x-3y)(xy2)2; (4)x(y-z)-y(z-x)+z(x-y).
解:(3)(x-3y)(xy2)2
=(x-3y) (x2y4)
=x x2y4+(-3y) x2y4
=x3y4-3x2y3.
(4)x(y-z)-y(z-x)+z(x-y)
=xy+x(-z)+(-y)z+(-y)(-x)+zx+z(-y)
=xy-xz-yz+xy+xz-yz
=2xy-2yz.
单项式与多项式相乘
单项式与单项式相乘
乘法分配律
转化
即时测评
①
②
③
下列各题的解法是否正确,如果错了,指出错在什么地方,并改正过来.
×
×
×
漏了单独字母
漏乘1
符号没有变化
例2 先化简,再求值:3a(2a2-4a+3)-2a2(3a+4), 其中a=-2.
当a=-2时,
解:3a(2a2-4a+3)-2a2(3a+4)
=6a3-12a2+9a-6a3-8a2
=-20a2+9a.
原式=-20×4-9×2=-98.
方法总结:在做乘法计算时,一定要注意单项式的符号和多项式中每一项的符号,不要搞错.
即时测评
先化简,再求值:x(x2-6x-9)-x(x2-8x-15)+2x(3-x),其中x=- .
解:x(x2-6x-9)-x(x2-8x-15)+2x(3-x)
=x3-6x2-9x-x3+8x2+15x+6x-2x2
=12x.
把x=- 代入得:原式=12x=12×(- )=-2.
例3 如果(-3x)2(x2-2nx+2)的展开式中不含x3项,求n的值.
方法总结:在整式乘法的混合运算中,要注意运算顺序.注意当要求多项式中不含有哪一项时,则表示这一项的系数为0.
解:(-3x)2(x2-2nx+2)
=9x2(x2-2nx+2)
=9x4-18nx3+18x2.
∵展开式中不含x3项,∴n=0.
单项式乘多项式的“两注意”
(1)乘积中每项的符号的确定:在确定积的每一项的符号时,
既要看多项式中每一项的符号,又要看单项式的符号,才能
正确确定积的每一项的符号.
(2)乘积的项数:非零单项式乘多项式,乘积仍是多项式,积
的项数与所乘多项式的项数相同.
归纳总结
当堂达标
叁
1. 下列计算正确的是( )
(A)-a(-a+b)=a2+ab
(B)x(-3x2+x-1)=-3x3+x2-1
(C)5m-2m(m-1)=3m2-3m
(D)(y-2y2+1)(-3y)=6y3-3y2-3y
2.如果ax(3x-4x2y+by2)=6x2-8x3y+6xy2成立,则( )
(A)a=3,b=2 (B)a=2,b=3 (C)a=-3,b=2 (D)a=-2,b=3
3.已知x2-2=y,则2x(x-3y)+2y(3x-1)-2是 .
当堂达标
B
D
2
(1) 4(a - b + 1) = ____________;
4a - 4b + 4
(2) 3x(2x - y2) = __________;
6x2 - 3xy2
(3) (2x - 5y + 6z)(-3x) = ________________;
-6x2 + 15xy - 18xz
(4) (-2a2)2(-a - 2b + c) = _________________.
-4a5 - 8a4b + 4a4c
4. 计算:
5. 计算:-2x2·(xy + y2)-5x(x2y-xy2).
解:原式 = (-2x2)·xy + (-2x2)·y2 + (-5x)·x2y + (-5x)·(-xy2)
= -2x3y + (-2x2y2) + (-5x3y) + 5x2y2
= -7x3y + 3x2y2.
6. 解方程:8x(5-x) = 34-2x(4x-3).
解得 x = 1.
解:去括号,得 40x-8x2 = 34-8x2 + 6x.
移项,得 40x-6x = 34.
合并同类项,得 34x = 34.
住宅用地
人民广场
商业用地
3a
3a + 2b
2a - b
4a
7. 如图,一块长方形地用来建造住宅、广场、商厦,
求这块地的总面积.
解:4a [(3a + 2b) + (2a-b)]
= 4a (5a + b)
= 4a · 5a + 4a · b
= 20a2 + 4ab.
答:这块地的总面积为
(20a2 + 4ab).
课堂小结
肆
课堂小结
单项式乘以多项式
转化
运用乘法分配律
单项式乘以单项式
课后作业
基础题:1.课后习题 第 2题。
提高题:2.请学有余力的同学完成课后习题第9题
谢
谢
同课章节目录
