16.2 整式的乘法 第3课时 多项式乘多项式 课件(共24张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 16.2 整式的乘法 第3课时 多项式乘多项式 课件(共24张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 22:52:18 | ||
图片预览








文档简介
(共24张PPT)
第16章 整式的乘法
16.2 整式的乘法
第3课时 多项式乘多项式
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
计算: x(3x2 xy 1).
解:原式= 3x3+x2y+x.
如何进行单项式与多项式乘法的运算?
① 用单项式去乘多项式的每一项;
② 再把所得的积相加.
进行单项式与多项式乘法运算时,要注意什么?
① 不能漏乘,即单项式要乘多项式的每一项;
② 去括号时注意符号的确定.
为了扩大街心花园的绿地面积,把一块原长为a m,宽为p m的长方形绿地,加长了b m,加宽了q m.求出扩大后的绿地面积
q
a
p
b
新知初探
贰
新知初探
任务一 探究多项式乘多项式的法则
活动1
你能用几种方法表示扩大后的绿地的面积 不同的表示方法之间有什么关系?
q
a
p
b
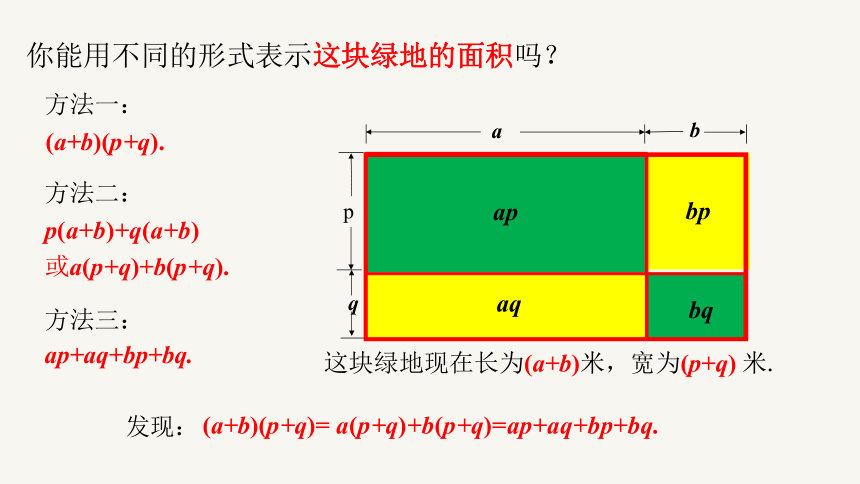
你能用不同的形式表示这块绿地的面积吗?
这块绿地现在长为(a+b)米,宽为(p+q) 米.
方法一:
(a+b)(p+q).
方法三:
ap+aq+bp+bq.
q
a
p
b
方法二:
p(a+b)+q(a+b)
或a(p+q)+b(p+q).
发现: (a+b)(p+q)= a(p+q)+b(p+q)=ap+aq+bp+bq.
ap
bq
aq
bp
活动2
你能证明(a+b)(p+q)=ap+aq+bp+bq吗?
如何进行多项式与多项式相乘的运算?
实际上,把(p+q)看成一个整体,有:
= ap+aq+bp+bq
(a+b)(p+q)
= a(p+q)+b(p+q)
(a+b)X=
aX+bX
?
若X=p+q,如何计算?
知识要点
一般地,多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
多项式乘以多项式
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
范例应用
例1 计算: (1)(a+3)(a-2); (2)(3x+1)(x+2);
(2) 原式=3x·x+2·3x+1·x+1×2
=3x2+6x+x+2
=3x2+7x+2;
解: (1) 原式= a·a+a·(-2)+3·a+3×(-2)
=a2-2a+3a-6
=a2+a-6
注意2:结果化 为最简形式!
注意1:计算时注意符号!
例1 计算: (3)(x-8y)(x-y); (4)(a+b)(a2-ab+b2)
(4) 原式= a·a2-a·ab+ab2+a2b-ab2+b·b2
=a3-a2b+ab2+a2b-ab2+b3
=a3+b3
解: (3) 原式=x·x-xy-8xy+8y2
=x2-9xy+8y2
注意3:不要漏 乘!
需要注意的几个问题:(1)漏乘;
(2)符号问题; (3)最后结果应化成最简形式.
注意
例2 计算:
(1)(3x+2y)(3x-2y);(2)(2ab-1)2; (3)(2a2-3a+5)(3-a).
需要注意的问题:
(1)漏乘;
(2)符号问题;
(3)最后结果应化成
最简形式.
解:(1)(3x+2y)(3x-2y)
=3x·3x+3x·(-2y)+2y·3x+2y·(-2y)
=9x2-6xy+6xy-4y2
=9x2-4y2.
(2)(2ab-1)2
=(2ab-1)(2ab-1)
=4a2b2-2ab-2ab+1
=4a2b2-4ab+1.
(3)(2a2-3a+5)(3-a)
=6a2-2a3-9a+3a2+15-5a
=-2a3+9a2-14a+15.
多项式乘多项式谨记“循序追乘”
多项式乘多项式,先用第一个多项式的第一项乘第二个多项
式的每一项,再用第一个多项式的第二项乘第二个多项式的
每一项……依次类推.
检验方法是若第一个多项式有x项,第二个多项式有y项,则
去括号后合并同类项前应共有xy项.
归纳总结
即时测评
判断下列解法是否正确,若错,请说出理由.
解:原式
漏
解:原式
当堂达标
叁
当堂达标
1.下列计算错误的是( )
A.(x+1)(x+4)=x2+5x+4 B.(y+4)(y-5)=y2+9y-20
C.(m-2)(m+3)=m2+m-6 D.(x-3)(x-6)=x2-9x+18
2.若(x+2)(x-1)=x2+mx+n,则m+n=( )
A.1 B.-2 C.-1 D.23.
3.
B
C
5
6
(-3)
-4
2
(-6)
(-5)
6
(a+b)
ab
观察上面四个等式,你能发现什么规律?
4.计算: (1) (3a+1)(a-2) ; (2) (1-x+y)(-x-y).
解:(1) (3a+1)(a-2)
= 3a a+3a (-2)+1 a+ 1 (-2)
= 3a2-6a+a-2
= 3a2-5a-2 ;
(2) (1-x+y)(-x-y)
=-x-y+x2+xy-xy-y2
=-x-y+x2-y2 .
5.化简求值:
(4x+3y)(4x-3y)+(2x+y)(3x-5y),其中x=1,y=-2.
当x=1,y=-2时,
原式=22×1-7×1×(-2)-14×(-2)2
=22+14 -56
=-20.
解:原式=
课堂小结
肆
课堂小结
多项式×多项式
运算法则
,先用一个多项式的每一项分 的每一项,再把所得的积相加.
多项式与多项式相乘
别乘以另一个多项式
(a+b)(p+q)=ap+aq+bp+bq.
注
意
不要漏乘.
实质上是转化为单项式×多项式的运算.
正确确定各项符号.
结果要最简(合并同类项).
课后作业
基础题:1.课后习题 第 3题。
提高题:2.请学有余力的同学完成课后习题第11题
谢
谢
第16章 整式的乘法
16.2 整式的乘法
第3课时 多项式乘多项式
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
计算: x(3x2 xy 1).
解:原式= 3x3+x2y+x.
如何进行单项式与多项式乘法的运算?
① 用单项式去乘多项式的每一项;
② 再把所得的积相加.
进行单项式与多项式乘法运算时,要注意什么?
① 不能漏乘,即单项式要乘多项式的每一项;
② 去括号时注意符号的确定.
为了扩大街心花园的绿地面积,把一块原长为a m,宽为p m的长方形绿地,加长了b m,加宽了q m.求出扩大后的绿地面积
q
a
p
b
新知初探
贰
新知初探
任务一 探究多项式乘多项式的法则
活动1
你能用几种方法表示扩大后的绿地的面积 不同的表示方法之间有什么关系?
q
a
p
b
你能用不同的形式表示这块绿地的面积吗?
这块绿地现在长为(a+b)米,宽为(p+q) 米.
方法一:
(a+b)(p+q).
方法三:
ap+aq+bp+bq.
q
a
p
b
方法二:
p(a+b)+q(a+b)
或a(p+q)+b(p+q).
发现: (a+b)(p+q)= a(p+q)+b(p+q)=ap+aq+bp+bq.
ap
bq
aq
bp
活动2
你能证明(a+b)(p+q)=ap+aq+bp+bq吗?
如何进行多项式与多项式相乘的运算?
实际上,把(p+q)看成一个整体,有:
= ap+aq+bp+bq
(a+b)(p+q)
= a(p+q)+b(p+q)
(a+b)X=
aX+bX
?
若X=p+q,如何计算?
知识要点
一般地,多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
多项式乘以多项式
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
范例应用
例1 计算: (1)(a+3)(a-2); (2)(3x+1)(x+2);
(2) 原式=3x·x+2·3x+1·x+1×2
=3x2+6x+x+2
=3x2+7x+2;
解: (1) 原式= a·a+a·(-2)+3·a+3×(-2)
=a2-2a+3a-6
=a2+a-6
注意2:结果化 为最简形式!
注意1:计算时注意符号!
例1 计算: (3)(x-8y)(x-y); (4)(a+b)(a2-ab+b2)
(4) 原式= a·a2-a·ab+ab2+a2b-ab2+b·b2
=a3-a2b+ab2+a2b-ab2+b3
=a3+b3
解: (3) 原式=x·x-xy-8xy+8y2
=x2-9xy+8y2
注意3:不要漏 乘!
需要注意的几个问题:(1)漏乘;
(2)符号问题; (3)最后结果应化成最简形式.
注意
例2 计算:
(1)(3x+2y)(3x-2y);(2)(2ab-1)2; (3)(2a2-3a+5)(3-a).
需要注意的问题:
(1)漏乘;
(2)符号问题;
(3)最后结果应化成
最简形式.
解:(1)(3x+2y)(3x-2y)
=3x·3x+3x·(-2y)+2y·3x+2y·(-2y)
=9x2-6xy+6xy-4y2
=9x2-4y2.
(2)(2ab-1)2
=(2ab-1)(2ab-1)
=4a2b2-2ab-2ab+1
=4a2b2-4ab+1.
(3)(2a2-3a+5)(3-a)
=6a2-2a3-9a+3a2+15-5a
=-2a3+9a2-14a+15.
多项式乘多项式谨记“循序追乘”
多项式乘多项式,先用第一个多项式的第一项乘第二个多项
式的每一项,再用第一个多项式的第二项乘第二个多项式的
每一项……依次类推.
检验方法是若第一个多项式有x项,第二个多项式有y项,则
去括号后合并同类项前应共有xy项.
归纳总结
即时测评
判断下列解法是否正确,若错,请说出理由.
解:原式
漏
解:原式
当堂达标
叁
当堂达标
1.下列计算错误的是( )
A.(x+1)(x+4)=x2+5x+4 B.(y+4)(y-5)=y2+9y-20
C.(m-2)(m+3)=m2+m-6 D.(x-3)(x-6)=x2-9x+18
2.若(x+2)(x-1)=x2+mx+n,则m+n=( )
A.1 B.-2 C.-1 D.23.
3.
B
C
5
6
(-3)
-4
2
(-6)
(-5)
6
(a+b)
ab
观察上面四个等式,你能发现什么规律?
4.计算: (1) (3a+1)(a-2) ; (2) (1-x+y)(-x-y).
解:(1) (3a+1)(a-2)
= 3a a+3a (-2)+1 a+ 1 (-2)
= 3a2-6a+a-2
= 3a2-5a-2 ;
(2) (1-x+y)(-x-y)
=-x-y+x2+xy-xy-y2
=-x-y+x2-y2 .
5.化简求值:
(4x+3y)(4x-3y)+(2x+y)(3x-5y),其中x=1,y=-2.
当x=1,y=-2时,
原式=22×1-7×1×(-2)-14×(-2)2
=22+14 -56
=-20.
解:原式=
课堂小结
肆
课堂小结
多项式×多项式
运算法则
,先用一个多项式的每一项分 的每一项,再把所得的积相加.
多项式与多项式相乘
别乘以另一个多项式
(a+b)(p+q)=ap+aq+bp+bq.
注
意
不要漏乘.
实质上是转化为单项式×多项式的运算.
正确确定各项符号.
结果要最简(合并同类项).
课后作业
基础题:1.课后习题 第 3题。
提高题:2.请学有余力的同学完成课后习题第11题
谢
谢
同课章节目录
