16.2 整式的乘法 第5课时 整式的除法 课件(共27张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 16.2 整式的乘法 第5课时 整式的除法 课件(共27张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 22:56:46 | ||
图片预览








文档简介
(共27张PPT)
第16章 整式的乘法
16.2 整式的乘法
第5课时 整式的除法
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
问题 木星的质量约是1.9×1024吨,地球的质量约是5.98×1021吨,
你知道木星的质量约为地球质量的多少倍吗
木星的质量约为地球质量的(1.90×1024)÷(5.98×1021)倍.
想一想:上面的式子该如何计算
地球
木星
新知初探
贰
新知初探
任务一 探究单项式除以单项式的法则
活动1
(1)计算:4a2x3·3ab2.
解:原式=4×3a2+1b2x3=12a3b2x3.
(2)问题:( )·3ab2=12a3b2x3,
括号内应填写什么?你是怎么得到这个答案的?
4a2x3
法则:
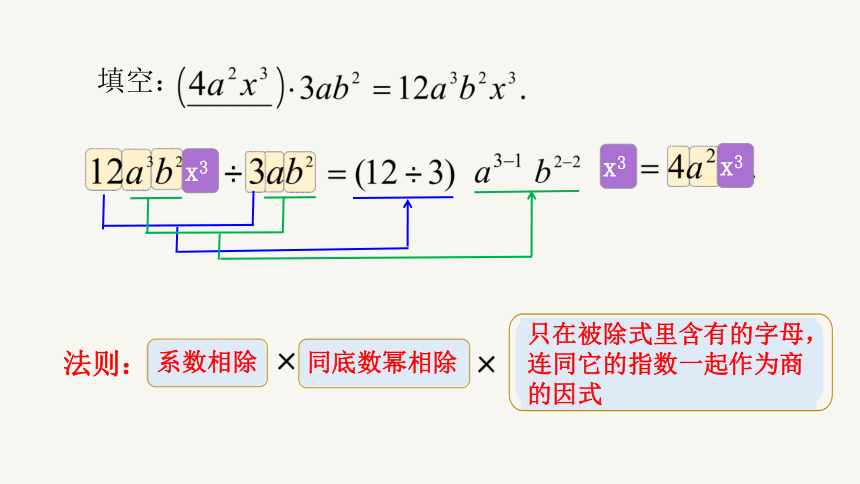
填空:
系数相除
同底数幂相除
只在被除式里含有的字母,连同它的指数一起作为商的因式
x3
x3
x3
知识要点
一般地,单项式相除, 把系数、同底数的幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连它的指数一起作为商的一个因式.
单项式除以单项式的法则
底数不变,
指数相减.
保留在商里
作为因式.
被除式的系数
除式的系数
理解:
商式=系数 同底的幂 被除式里单独有的幂
范例应用
例1 计算
⑴ 24a3b2÷3ab2
解:(1)原式=(24÷3) (a3÷a) (b2÷b2)
=8a3-1·1
=8a2
注意:b2÷b2=1
(2)28x4y2 ÷7x3y;
(3)-5a5b3c ÷15a4b.
=4xy;
(3)原式=(-5÷15)a5-4b3-1c
解:(2)原式=(28 ÷7)x4-3y2-1
= ab2c.
即时测评
计算:
(1)(- x2y3)÷3x2y; (2)(10a4b3c2)÷5a3bc; (3)(-3x3y2)3÷9x2y3.
解:(1)(- x2y3)÷3x2y=[(- )÷3] x2-2y3-1=- y2.
(2)(10a4b3c2)÷5a3bc
=(10÷5) .a4-3b3-1c2-1
=2ab2c.
(3)(-3x3y2)3÷9x2y3=-27x9y6÷9x2y3=-3x7y3.
方法总结:掌握整式的除法的运算法则是解题的关键,注意在计算过程中,有乘方的先算乘方,再算乘除.
单项式除以单项式的“三注意”
(1)系数相除作为商的系数,系数包括前面的符号,应先确定
商的符号;
(2)含有相同字母的部分按同底数幂的除法法则进行运算,即
底数不变,指数相减;
(3)单独在被除式中出现的字母不能漏掉,要连同它的指数直
接作为商的一个因式.
归纳总结
任务二 探究多项式除以单项式的法则
活动1
问题1 若已知油画的面积为(ma+mb),宽为m,
如何求它的长?请列出算式.
(ma+mb)÷m
问题2 如何计算(am+bm) ÷m
计算(am+bm) ÷m就是相当于求( ) ·m=am+bm,因此不难想到 括号里应填a+b.
又因为am ÷m+bm ÷m=a+b.
所以 (am+bm) ÷m=am ÷m+bm ÷m
多项式除以单项式的法则
一般地,多项式除以单项式,就是用多项式的 除以这个 ,再把所得的商 .
单项式
每一项
相加
关键:
应用法则是把多项式除以单项式转化为单项式除以单项式.
范例应用
例2 计算(12a3-6a2+3a) ÷3a.
解: (12a3-6a2+3a) ÷3a
=12a3÷3a+(-6a2) ÷3a+3a÷3a
=4a2+(-2a)+1
=4a2-2a+1.
方法总结:多项式除以单项式,实质是利用乘法的分配律,将多项式除以单项式问题转化为单项式除以单项式问题来解决.计算过程中,要注意符号问题.
即时测评
计算:
(1)(28a3-14a2)÷7a;
(2)(25m2+15m3n-20m4)÷(-5m2);
解:(1)原式=28a3÷7a-14a2÷7a=4a2-2a.
(2)原式=25m2÷(-5m2)+15m3n÷(-5m2)-20m4÷(-5m2)
=-5-3mn+4m2.
例3 先化简,后求值:[2x(x2y-xy2)+xy(xy-x2)]÷x2y,其中x=2025,y=2024.
解:原式=[2x3y-2x2y2+x2y2-x3y]÷x2y,
原式=x-y=2025-2024=1.
=x-y.
把x=2025,y=2024代入上式,得
多项式除以单项式的“四注意”
(1)多项式除以单项式要转化为单项式除以单项式;
(2)多项式是几项,所得的商就有几项;
(3)要注意商的符号,应弄清多项式中每一项的符号,相除时
要带着符号与单项式相除,注意符号的变化;
(4)注意运算顺序.
归纳总结
当堂达标
叁
当堂达标
1.下列算式中,不正确的是( )
A.(-12a5b)÷(-3ab)=4a4 B.9xmyn-1÷3xm-2yn-3=3x2y2
C.4a2b3÷2ab=2ab2 D.x(x-y)2÷(y-x)=x(x-y)
D
2.计算(3ab-2a)÷a的结果是( )
A.a B.b
C.3b-2 D.3b-2a
3.计算(6x3y-3xy2)÷3xy的结果是( )
A.6x2-y B.2x2-y
C.2x2+y D.2x2-xy
C
B
4.计算下列式子:
(1)8x6y3z2÷(-4x4y2 );
解: (1)原式 =[8÷ (-4)]x6-4y3-2z2= -2x2yz2.
(2)25a2m+4b3n+5c ÷ 5a4bn+1c.
(2)原式=(25 ÷ 5) a2m+4-4b3n+5-n-1c1-1=5a2mb2n+4
(3)(36a4-12a3-8a)÷4a ; (4) (4xy4-2x2y3-8xy3z)÷2xy2.
(3)原式= 36a4÷4a+(-12a3)÷4a+(-8a)÷4a=9a3-3a2-2 ;
(4)原式= 4xy4÷2xy2+ (-2x2y3)÷2xy2+(-8xy3z)÷2xy2= 2y2-xy-4yz.
5.先化简,再求值:(x+y)(x-y)-(4x3y-8xy3)÷2xy,
其中x=1,y=-3.
解:原式=x2-y2-2x2+4y2
原式=-12+3×(-3)2=-1+27=26.
当x=1,y=-3时,
=-x2+3y2.
课堂小结
肆
课堂小结
多项式除以单项式
整 式 的 除 法
同底数幂相除
单项式相除
整 式 的 乘 法
(转化)
(转化)
课后作业
基础题:1.课后习题 第 4,5题。
提高题:2.请学有余力的同学完成课后习题第7题
谢
谢
第16章 整式的乘法
16.2 整式的乘法
第5课时 整式的除法
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
问题 木星的质量约是1.9×1024吨,地球的质量约是5.98×1021吨,
你知道木星的质量约为地球质量的多少倍吗
木星的质量约为地球质量的(1.90×1024)÷(5.98×1021)倍.
想一想:上面的式子该如何计算
地球
木星
新知初探
贰
新知初探
任务一 探究单项式除以单项式的法则
活动1
(1)计算:4a2x3·3ab2.
解:原式=4×3a2+1b2x3=12a3b2x3.
(2)问题:( )·3ab2=12a3b2x3,
括号内应填写什么?你是怎么得到这个答案的?
4a2x3
法则:
填空:
系数相除
同底数幂相除
只在被除式里含有的字母,连同它的指数一起作为商的因式
x3
x3
x3
知识要点
一般地,单项式相除, 把系数、同底数的幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连它的指数一起作为商的一个因式.
单项式除以单项式的法则
底数不变,
指数相减.
保留在商里
作为因式.
被除式的系数
除式的系数
理解:
商式=系数 同底的幂 被除式里单独有的幂
范例应用
例1 计算
⑴ 24a3b2÷3ab2
解:(1)原式=(24÷3) (a3÷a) (b2÷b2)
=8a3-1·1
=8a2
注意:b2÷b2=1
(2)28x4y2 ÷7x3y;
(3)-5a5b3c ÷15a4b.
=4xy;
(3)原式=(-5÷15)a5-4b3-1c
解:(2)原式=(28 ÷7)x4-3y2-1
= ab2c.
即时测评
计算:
(1)(- x2y3)÷3x2y; (2)(10a4b3c2)÷5a3bc; (3)(-3x3y2)3÷9x2y3.
解:(1)(- x2y3)÷3x2y=[(- )÷3] x2-2y3-1=- y2.
(2)(10a4b3c2)÷5a3bc
=(10÷5) .a4-3b3-1c2-1
=2ab2c.
(3)(-3x3y2)3÷9x2y3=-27x9y6÷9x2y3=-3x7y3.
方法总结:掌握整式的除法的运算法则是解题的关键,注意在计算过程中,有乘方的先算乘方,再算乘除.
单项式除以单项式的“三注意”
(1)系数相除作为商的系数,系数包括前面的符号,应先确定
商的符号;
(2)含有相同字母的部分按同底数幂的除法法则进行运算,即
底数不变,指数相减;
(3)单独在被除式中出现的字母不能漏掉,要连同它的指数直
接作为商的一个因式.
归纳总结
任务二 探究多项式除以单项式的法则
活动1
问题1 若已知油画的面积为(ma+mb),宽为m,
如何求它的长?请列出算式.
(ma+mb)÷m
问题2 如何计算(am+bm) ÷m
计算(am+bm) ÷m就是相当于求( ) ·m=am+bm,因此不难想到 括号里应填a+b.
又因为am ÷m+bm ÷m=a+b.
所以 (am+bm) ÷m=am ÷m+bm ÷m
多项式除以单项式的法则
一般地,多项式除以单项式,就是用多项式的 除以这个 ,再把所得的商 .
单项式
每一项
相加
关键:
应用法则是把多项式除以单项式转化为单项式除以单项式.
范例应用
例2 计算(12a3-6a2+3a) ÷3a.
解: (12a3-6a2+3a) ÷3a
=12a3÷3a+(-6a2) ÷3a+3a÷3a
=4a2+(-2a)+1
=4a2-2a+1.
方法总结:多项式除以单项式,实质是利用乘法的分配律,将多项式除以单项式问题转化为单项式除以单项式问题来解决.计算过程中,要注意符号问题.
即时测评
计算:
(1)(28a3-14a2)÷7a;
(2)(25m2+15m3n-20m4)÷(-5m2);
解:(1)原式=28a3÷7a-14a2÷7a=4a2-2a.
(2)原式=25m2÷(-5m2)+15m3n÷(-5m2)-20m4÷(-5m2)
=-5-3mn+4m2.
例3 先化简,后求值:[2x(x2y-xy2)+xy(xy-x2)]÷x2y,其中x=2025,y=2024.
解:原式=[2x3y-2x2y2+x2y2-x3y]÷x2y,
原式=x-y=2025-2024=1.
=x-y.
把x=2025,y=2024代入上式,得
多项式除以单项式的“四注意”
(1)多项式除以单项式要转化为单项式除以单项式;
(2)多项式是几项,所得的商就有几项;
(3)要注意商的符号,应弄清多项式中每一项的符号,相除时
要带着符号与单项式相除,注意符号的变化;
(4)注意运算顺序.
归纳总结
当堂达标
叁
当堂达标
1.下列算式中,不正确的是( )
A.(-12a5b)÷(-3ab)=4a4 B.9xmyn-1÷3xm-2yn-3=3x2y2
C.4a2b3÷2ab=2ab2 D.x(x-y)2÷(y-x)=x(x-y)
D
2.计算(3ab-2a)÷a的结果是( )
A.a B.b
C.3b-2 D.3b-2a
3.计算(6x3y-3xy2)÷3xy的结果是( )
A.6x2-y B.2x2-y
C.2x2+y D.2x2-xy
C
B
4.计算下列式子:
(1)8x6y3z2÷(-4x4y2 );
解: (1)原式 =[8÷ (-4)]x6-4y3-2z2= -2x2yz2.
(2)25a2m+4b3n+5c ÷ 5a4bn+1c.
(2)原式=(25 ÷ 5) a2m+4-4b3n+5-n-1c1-1=5a2mb2n+4
(3)(36a4-12a3-8a)÷4a ; (4) (4xy4-2x2y3-8xy3z)÷2xy2.
(3)原式= 36a4÷4a+(-12a3)÷4a+(-8a)÷4a=9a3-3a2-2 ;
(4)原式= 4xy4÷2xy2+ (-2x2y3)÷2xy2+(-8xy3z)÷2xy2= 2y2-xy-4yz.
5.先化简,再求值:(x+y)(x-y)-(4x3y-8xy3)÷2xy,
其中x=1,y=-3.
解:原式=x2-y2-2x2+4y2
原式=-12+3×(-3)2=-1+27=26.
当x=1,y=-3时,
=-x2+3y2.
课堂小结
肆
课堂小结
多项式除以单项式
整 式 的 除 法
同底数幂相除
单项式相除
整 式 的 乘 法
(转化)
(转化)
课后作业
基础题:1.课后习题 第 4,5题。
提高题:2.请学有余力的同学完成课后习题第7题
谢
谢
同课章节目录
