16.3.2 完全平方公式 第2课时 乘法公式的综合 课件(共26张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 16.3.2 完全平方公式 第2课时 乘法公式的综合 课件(共26张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1013.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 23:00:10 | ||
图片预览







文档简介
(共26张PPT)
第16章 整式的乘法
16.3.2 完全平方公式
第2课时 乘法公式的综合
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
一、平方差公式用字母怎么表示?
(a+b)(a-b)=a2-b2.
二、完全平方公式用字母怎么表示?
(a+b)2=a2+2ab+b2, (a-b)2=a2-2ab+b2.
三、利用平方差公式和完全平方公式填一填:
1. [ x +( 2y-3)] [ x- (2y -3)]= 2- ( )2;
2.(2y-3)2=
4y2-12y + 9 .
温馨提示:
将(2y – 3)看作一个整 体,解题中渗透整体的思想.
x
2y-3
新知初探
贰
新知初探
任务一 添括号法则
活动1
①如果括号前面是“+”号,去括号时括号里各项都 .
②如果括号前面是“-”号,去括号时括号里各项都 .
问题1 去括号法则是什么?
去括号就是用括号外的数乘括号内的每一项,再把所得的积相加.
不改变符号
改变符号
(1) a + (b – c) = ;
(2) a – (b – c ) = .
从等号左边到右边属于去括号. 从等号左边到右边属于添括号.
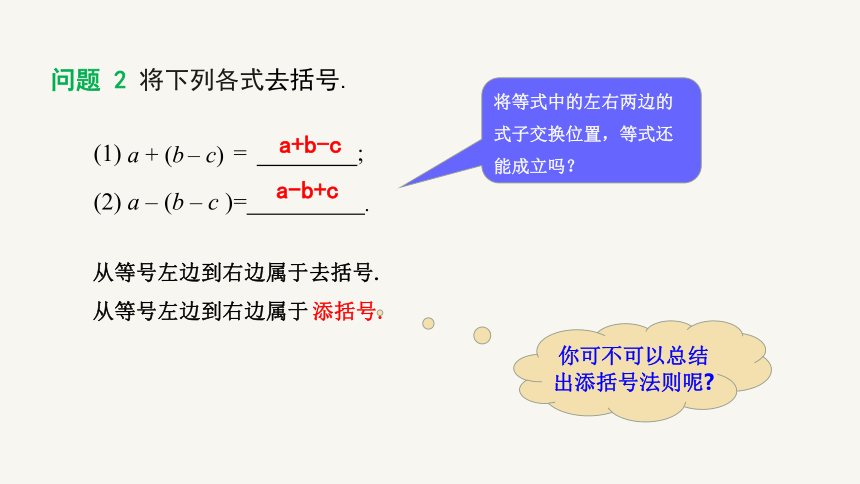
问题 2 将下列各式去括号.
a+b-c
a-b+c
将等式中的左右两边的式子交换位置,等式还能成立吗?
你可不可以总结出添括号法则呢
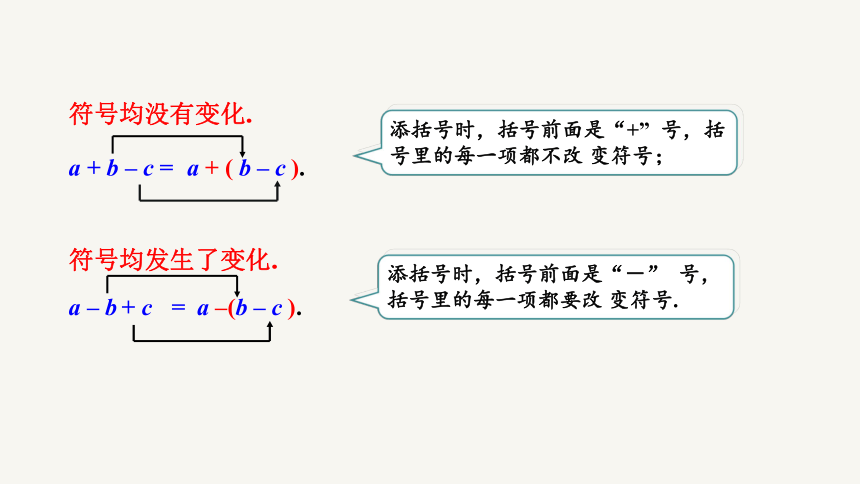
符号均没有变化.
a + b – c = a + ( b – c ).
符号均发生了变化.
a – b + c = a –(b – c ).
添括号时,括号前面是“+” 号,括号里的每一项都不改 变符号;
添括号时,括号前面是“-” 号,括号里的每一项都要改 变符号.
添括号时,如果括号前面是正号,括到括号里的各项都不变号;如果括号前面是负号,括到括号里的各项都改变符号(简记为“负变正不变”).
添括号法则
即时测评
在等号右边的括号内填上适当的项,并用去括号法则检验.
(1)a+b+c=a+( );a-b-c=a-( );
a-b+c=a-( );a+b-c=a+( ).
(2)x+2y-3=x+( );x-2y+3=x-( );
a+2b-1=( )–1;2a-b-c=2a-( ).
b+c
b+c
b-c
b-c
2y-3
2y-3
a+2b
b+c
范例应用
例1 运用乘法公式计算:
( x +2y-3) (x- 2y +3) .
温馨提示:将(2y – 3 )看作一个 整体,应用了整体的数学思想.
解:原式= [ x+ (2y – 3)] [ x-(2y-3) ]
= x2-(2y-3)2
= x2-( 4y2-12y + 9)
= x2-4y2+12y-9.
观察并比较两个因式的各项,你能发现什么
平方差公式
(a+b)(a-b)=a2-b2中的a和b在本题中分别是什么?
添括号将下列各式变形为可利用平方差公式计算的形式:
(1)(x+2y+3)(x+2y-3);
(2)(x+2y-3)(x-2y+3);
(3)(x-2y+3)(x-2y-3);
(4)(x-2y-3)(x+2y-3).
解:原式=[(x+2y)+3][(x+2y)-3];
即时测评
解:原式=[(x-2y)+3] [(x-2y)-3];
解:原式=[(x-3)-2y] [(x-3)+2y].
a
b
解:原式=[x+(2y-3)] [x-(2y-3)];
a
b
a
b
a
b
a
b
a
b
a
b
a
b
在乘法公式中添括号的“两种技巧”
(1)当两个三项式相乘,且它们只含相同项与相反项时,通过
添括号把相同项、相反项分别结合,一个化为“和”的形式,
一个化为“差”的形式,可利用平方差公式;
(2)一个三项式的平方,通过添括号把其中两项看成一个整体,
可利用完全平方公式.
归纳总结
范例应用
例2 运用乘法公式计算:(a+b+c)2.
解: (a+b+c)2
=[(a+b)+c]2
=(a+b)2+2(a+b)c+c2
=a2+2ab+b2+2ac+2bc+c2
=a2+b2+c2+2ab+2bc+2ac.
温馨提示:将(a+b)看作一个整体, 解题中渗透整体的思想.
本题还有没有第二种做法?
例2 运用乘法公式计算:(a+b+c)2.
解:(a+b+c)2
=[a+(b+c)]2
=a2+2a(b+c)+(b+c)2
=a2+2ab+2ac+b2+2bc+c2
=a2+b2+c2+2ab+2bc+2ac.
即时测评
运用乘法公式计算:(m+2n-p)2.
解:(m+2n-p)2
=[(m+2n)-p]2
=(m+2n)2-2p(m+2n)+p2
=m2+4mn+4n2-2pm-4pn+p2.
当堂达标
叁
当堂达标
C
1.与x3-2x2-4x+8相等的是( )
A.(x3-2x2)-(-4x+8)
B.x3+8+(-2x2+4x)
C.(x3-2x2)-(4x-8)
D.x3+8-(2x2-4x)
2.为了应用平方差公式计算(x+3y-1)(x-3y+1),下列变形正确的是( )
A.[x-(3y+1)]2
B.[x+(3y+1)]2
C.[x+(3y-1)][x-(3y-1)]
D.[(x-3y)+1][(x-3y)-1]
C
3.添括号:2024a-b+2025c=2024a-(___________).
b-2025c
4.计算:
(1)(a-2b+3c)(a+2b-3c);
(2)(3x-2y+1)2.
解:(1)(a-2b+3c)(a+2b-3c)
=[a-(2b-3c)][a+(2b-3c)]
=a2-(2b-3c)2
=a2-(4b2-12bc+9c2)
=a2-4b2+12bc-9c2.
(2)(3x-2y+1)2=[(3x-2y)+1]2
=(3x-2y)2+2×1×(3x-2y)+12
=9x2-12xy+4y2+6x-4y+1.
5.计算:(a-b+c)2.
解:(a-b+c)2
=[a-(b+c)]2
=a2-2a(b+c)+(b+c)2
=a2-2ab-2ac+b2+2bc+c2
=a2+b2+c2-2ab-2ac+2bc.
以上解答过程正确吗 若不正确,请指出错在哪里,并写出正确的解答过程.
解:将-b+c添括号时出错,正确的解答过程如下:
(a-b+c)2=[a-(b-c)]2=a2-2a(b-c)+(b-c)2=a2-2ab+2ac+b2-2bc+c2=a2+b2+c2-2ab+2ac-2bc.
课堂小结
肆
课堂小结
添括号时,如果括号前面是正号,括到括号里的各项都不变号;如果括号前面是负号,括到括号里的各项都改变符号(简记为“负变正不变”).
添括号法则
a + b + c = a + ( b + c) ;
a – b – c = a – ( b + c ) .
课后作业
基础题:1.课后习题 第 3,4题。
提高题:2.请学有余力的同学完成课后习题第8题
谢
谢
第16章 整式的乘法
16.3.2 完全平方公式
第2课时 乘法公式的综合
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
一、平方差公式用字母怎么表示?
(a+b)(a-b)=a2-b2.
二、完全平方公式用字母怎么表示?
(a+b)2=a2+2ab+b2, (a-b)2=a2-2ab+b2.
三、利用平方差公式和完全平方公式填一填:
1. [ x +( 2y-3)] [ x- (2y -3)]= 2- ( )2;
2.(2y-3)2=
4y2-12y + 9 .
温馨提示:
将(2y – 3)看作一个整 体,解题中渗透整体的思想.
x
2y-3
新知初探
贰
新知初探
任务一 添括号法则
活动1
①如果括号前面是“+”号,去括号时括号里各项都 .
②如果括号前面是“-”号,去括号时括号里各项都 .
问题1 去括号法则是什么?
去括号就是用括号外的数乘括号内的每一项,再把所得的积相加.
不改变符号
改变符号
(1) a + (b – c) = ;
(2) a – (b – c ) = .
从等号左边到右边属于去括号. 从等号左边到右边属于添括号.
问题 2 将下列各式去括号.
a+b-c
a-b+c
将等式中的左右两边的式子交换位置,等式还能成立吗?
你可不可以总结出添括号法则呢
符号均没有变化.
a + b – c = a + ( b – c ).
符号均发生了变化.
a – b + c = a –(b – c ).
添括号时,括号前面是“+” 号,括号里的每一项都不改 变符号;
添括号时,括号前面是“-” 号,括号里的每一项都要改 变符号.
添括号时,如果括号前面是正号,括到括号里的各项都不变号;如果括号前面是负号,括到括号里的各项都改变符号(简记为“负变正不变”).
添括号法则
即时测评
在等号右边的括号内填上适当的项,并用去括号法则检验.
(1)a+b+c=a+( );a-b-c=a-( );
a-b+c=a-( );a+b-c=a+( ).
(2)x+2y-3=x+( );x-2y+3=x-( );
a+2b-1=( )–1;2a-b-c=2a-( ).
b+c
b+c
b-c
b-c
2y-3
2y-3
a+2b
b+c
范例应用
例1 运用乘法公式计算:
( x +2y-3) (x- 2y +3) .
温馨提示:将(2y – 3 )看作一个 整体,应用了整体的数学思想.
解:原式= [ x+ (2y – 3)] [ x-(2y-3) ]
= x2-(2y-3)2
= x2-( 4y2-12y + 9)
= x2-4y2+12y-9.
观察并比较两个因式的各项,你能发现什么
平方差公式
(a+b)(a-b)=a2-b2中的a和b在本题中分别是什么?
添括号将下列各式变形为可利用平方差公式计算的形式:
(1)(x+2y+3)(x+2y-3);
(2)(x+2y-3)(x-2y+3);
(3)(x-2y+3)(x-2y-3);
(4)(x-2y-3)(x+2y-3).
解:原式=[(x+2y)+3][(x+2y)-3];
即时测评
解:原式=[(x-2y)+3] [(x-2y)-3];
解:原式=[(x-3)-2y] [(x-3)+2y].
a
b
解:原式=[x+(2y-3)] [x-(2y-3)];
a
b
a
b
a
b
a
b
a
b
a
b
a
b
在乘法公式中添括号的“两种技巧”
(1)当两个三项式相乘,且它们只含相同项与相反项时,通过
添括号把相同项、相反项分别结合,一个化为“和”的形式,
一个化为“差”的形式,可利用平方差公式;
(2)一个三项式的平方,通过添括号把其中两项看成一个整体,
可利用完全平方公式.
归纳总结
范例应用
例2 运用乘法公式计算:(a+b+c)2.
解: (a+b+c)2
=[(a+b)+c]2
=(a+b)2+2(a+b)c+c2
=a2+2ab+b2+2ac+2bc+c2
=a2+b2+c2+2ab+2bc+2ac.
温馨提示:将(a+b)看作一个整体, 解题中渗透整体的思想.
本题还有没有第二种做法?
例2 运用乘法公式计算:(a+b+c)2.
解:(a+b+c)2
=[a+(b+c)]2
=a2+2a(b+c)+(b+c)2
=a2+2ab+2ac+b2+2bc+c2
=a2+b2+c2+2ab+2bc+2ac.
即时测评
运用乘法公式计算:(m+2n-p)2.
解:(m+2n-p)2
=[(m+2n)-p]2
=(m+2n)2-2p(m+2n)+p2
=m2+4mn+4n2-2pm-4pn+p2.
当堂达标
叁
当堂达标
C
1.与x3-2x2-4x+8相等的是( )
A.(x3-2x2)-(-4x+8)
B.x3+8+(-2x2+4x)
C.(x3-2x2)-(4x-8)
D.x3+8-(2x2-4x)
2.为了应用平方差公式计算(x+3y-1)(x-3y+1),下列变形正确的是( )
A.[x-(3y+1)]2
B.[x+(3y+1)]2
C.[x+(3y-1)][x-(3y-1)]
D.[(x-3y)+1][(x-3y)-1]
C
3.添括号:2024a-b+2025c=2024a-(___________).
b-2025c
4.计算:
(1)(a-2b+3c)(a+2b-3c);
(2)(3x-2y+1)2.
解:(1)(a-2b+3c)(a+2b-3c)
=[a-(2b-3c)][a+(2b-3c)]
=a2-(2b-3c)2
=a2-(4b2-12bc+9c2)
=a2-4b2+12bc-9c2.
(2)(3x-2y+1)2=[(3x-2y)+1]2
=(3x-2y)2+2×1×(3x-2y)+12
=9x2-12xy+4y2+6x-4y+1.
5.计算:(a-b+c)2.
解:(a-b+c)2
=[a-(b+c)]2
=a2-2a(b+c)+(b+c)2
=a2-2ab-2ac+b2+2bc+c2
=a2+b2+c2-2ab-2ac+2bc.
以上解答过程正确吗 若不正确,请指出错在哪里,并写出正确的解答过程.
解:将-b+c添括号时出错,正确的解答过程如下:
(a-b+c)2=[a-(b-c)]2=a2-2a(b-c)+(b-c)2=a2-2ab+2ac+b2-2bc+c2=a2+b2+c2-2ab+2ac-2bc.
课堂小结
肆
课堂小结
添括号时,如果括号前面是正号,括到括号里的各项都不变号;如果括号前面是负号,括到括号里的各项都改变符号(简记为“负变正不变”).
添括号法则
a + b + c = a + ( b + c) ;
a – b – c = a – ( b + c ) .
课后作业
基础题:1.课后习题 第 3,4题。
提高题:2.请学有余力的同学完成课后习题第8题
谢
谢
同课章节目录
