17.1 用提公因式法分解因式 第1课时 因式分解与提公因式法 课件(共25张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 17.1 用提公因式法分解因式 第1课时 因式分解与提公因式法 课件(共25张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 23:01:49 | ||
图片预览








文档简介
(共25张PPT)
第17章 因式分解
17.1 用提公因式法分解因式
第1课时
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
思考:630能被哪些数整除?
把630分解质因数,可以得到:
630 = 2 × 9 × 5 × 7
一个数可以写成若干个因数乘积的形式,一个整式 能不能这样做呢?
新知初探
贰
新知初探
反过来成立吗?你得到了什么?
1.如图,一块菜地被分成三部分,你能用不同的方式表示这块草坪的面积吗?
a
b
c
p
方法一:p(a+b+c)
方法二:pa+pb+pc
p(a+b+c)=pa+pb+pc
整式乘法
任务一 探究因式分解的概念
活动1
(2)(x+1)(x-1)= ;
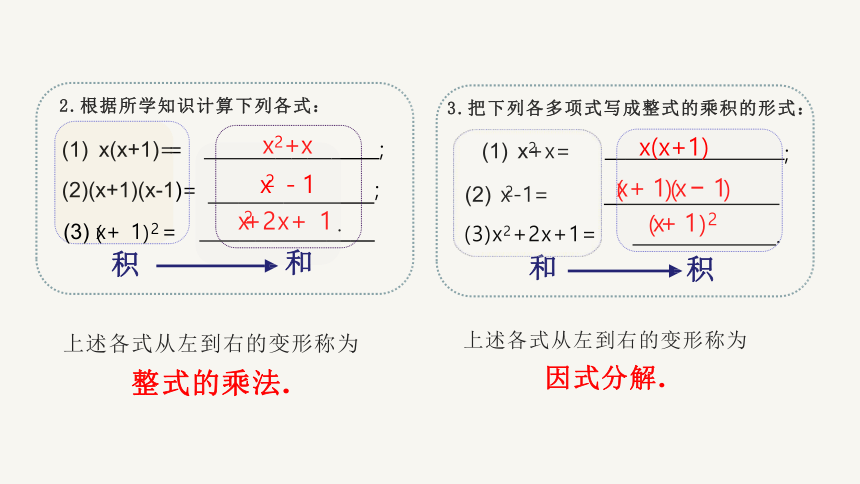
2.根据所学知识计算下列各式:
3.把下列各多项式写成整式的乘积的形式:
(1) x(x+1)==
;
x2+x
x2 +2x+ 1 .
;
(2) x2 -1=
.
(1) x2 +x=
(x + 1)(x 1)
( x+ 1)2
上述各式从左到右的变形称为
因式分解.
上述各式从左到右的变形称为
整式的乘法.
和
(3) (x + 1)2 =
积
和
x2 - 1
积
(3)x2+2x+1=
x(x+1)
把一个多项式化为几个整式的乘积的形式,像这样的式子变形叫作把这个多项式因式分解,也叫作把这个多项式分解因式.
归纳总结
x2–1 (x+1)(x–1)
因式分解
整式乘法
x2–1 = (x+1)(x–1)
等式的特征:左边是多项式,右边是几个整式的乘积
整式乘法与因式分解有什么关系?
是互为相反的变形,即
想一想
和
积
例1 下列从左到右的变形中是因式分解的有( )
①x2-y2-1=(x+y)(x-y)-1;②x3+x=x(x2+1);③(x-y)2=x2-2xy+y2;④x2-9y2=(x+3y)(x-3y).
A.1个 B.2个 C.3个 D.4个
范例应用
B
结果为积形式.
1.分清题目要求是整式乘法还是因式分解;
2.因式分解的结果必须是乘积形式.
方法总结:因式分解与整式乘法是相反方向的变形,即互逆运算,二者是一个式子的不同表现形式.因式分解的右边是两个或几个因式积的形式,整式乘法的右边是多项式的形式.
即时测评
下列等式从左到右的变形,属于因式分解的是( )
A.(a+b)(a﹣b)=a2﹣b2
B.x2+2x﹣1=(x+1)(x﹣1)+2x
C.m2﹣4m+4=m(m﹣4)+4
D.﹣6x2+3x=﹣3x(2x﹣1)
D
任务二 提取公因式法
活动1
2.根据上题的启发,试一试因式分解:
逆用乘法分配律
1.请用简便的方法计算 365 × 37 + 365 × 63,
思考在简便运算中运用了什么运算法则?
= 365 × (37 + 63)
= 365 × 100
= 36500.
ma+mb.
365 × 37 + 365 × 63
ma+mb
=ma+mb
=m(a+b)
365×37+365×63
=365×(37+63)
=365×100
=36500
逆用乘法分配律
公因式 m
多项式中各项都含有的公共因式,
叫作这个多项式各项的公因式
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫作提公因式法.
( a+b+c )
pa+ pb +pc
p
=
pa+pb+pc
相同因式p
范例应用
公因式是m
【例2】分解因式:
(1)mx2+my2; (2)3x2-4xy2+x.
解:(1)mx2+my2
=m x2+m y2
=m(x2-y2).
(2)3x2-4xy2+x
=x 3x-x 4y2+x 1
=x(3x-4y2+1).
公因式是x
即时测评
把下列各式分解因式:
(1)ax+ay;
(2)a2b2+ab-a;
(3)21xy-14xz+x2;
(4)2mn-4m2n+m.
解:(1)ax+ay=a(x+y).
(2)a2b2+ab-a=a(ab2+b-1).
(3)21xy-14xz+x2=x(21y-14z+x).
(4)2mn-4m2n+m=m(2n-4mn+1).
当堂达标
叁
当堂达标
1. 下列由左到右的变形,属于因式分解的是( )
A.(x+2)(x﹣2)=x2﹣4
B.x2﹣4=(x+2)(x﹣2)
C.x2﹣4+3x=(x+2)(x﹣2)+3x
D.x2+4x﹣2=x(x+4)﹣2
2.下列分解因式正确的是( )
(A)2x2-xy-x=x(x-y-1)
(B)xy2+2xy-3y=y(xy+2x+3)
(C)x2-xy=x(x-y)
(D)x2-x-3=x(x-1)-3
B
C
3.在下列等式中,从左到右的变形是因式分解的有 ,不是的,请说明为什么?
①
②
③
④
⑤
⑥
③
⑥
am+bm+c=m(a+b)+c
24x2y=3x ·8xy
x2-1=(x+1)(x-1)
(2x+1)2=4x2+4x+1
x2+x=x2(1+ )
2x+4y+6z=2(x+2y+3z)
最后不是积的运算
因式分解的对象是多项式,
是整式乘法
每个因式必须是整式
4.把下列各式分解因式:
(1)a2+5a;
(2)x2﹣2x;
(3)a2+ab﹣a;
(4)4x2+6xy-x.
解:(1)a2+5a=a(a+5).
(2)x2﹣2x=x(x﹣2).
(3)a2+ab﹣a=a(a+b﹣1).
(4)4x2+6xy-x=x(4x+6y-1).
5.利用因式分解进行简便计算:
(1)23.7×1.6+8.4×23.7;
(2)34.3×17.1+82.5×17.1-268×1.71+171.
解:(1)23.7×1.6+8.4×23.7
=23.7×(1.6+8.4)
=23.7×10
=237.
(2)34.3×17.1+82.5×17.1-268×1.71+171
=34.3×17.1+82.5×17.1-26.8×17.1+10×17.1
=17.1×(34.3+82.5-26.8+10)
=17.1×100
=1 710.
课堂小结
肆
课堂小结
1. 因式分解与整式乘法是一个互逆过程,即:
因式分解
整式乘法
几个整式相乘
一个多项式
提公因式法
分两步:
第一步找公因式;第二步提公因式
2.
课后作业
基础题:1.课后习题 第 1,2题。
提高题:2.请学有余力的同学完成课后习题第3题
谢
谢
第17章 因式分解
17.1 用提公因式法分解因式
第1课时
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
思考:630能被哪些数整除?
把630分解质因数,可以得到:
630 = 2 × 9 × 5 × 7
一个数可以写成若干个因数乘积的形式,一个整式 能不能这样做呢?
新知初探
贰
新知初探
反过来成立吗?你得到了什么?
1.如图,一块菜地被分成三部分,你能用不同的方式表示这块草坪的面积吗?
a
b
c
p
方法一:p(a+b+c)
方法二:pa+pb+pc
p(a+b+c)=pa+pb+pc
整式乘法
任务一 探究因式分解的概念
活动1
(2)(x+1)(x-1)= ;
2.根据所学知识计算下列各式:
3.把下列各多项式写成整式的乘积的形式:
(1) x(x+1)==
;
x2+x
x2 +2x+ 1 .
;
(2) x2 -1=
.
(1) x2 +x=
(x + 1)(x 1)
( x+ 1)2
上述各式从左到右的变形称为
因式分解.
上述各式从左到右的变形称为
整式的乘法.
和
(3) (x + 1)2 =
积
和
x2 - 1
积
(3)x2+2x+1=
x(x+1)
把一个多项式化为几个整式的乘积的形式,像这样的式子变形叫作把这个多项式因式分解,也叫作把这个多项式分解因式.
归纳总结
x2–1 (x+1)(x–1)
因式分解
整式乘法
x2–1 = (x+1)(x–1)
等式的特征:左边是多项式,右边是几个整式的乘积
整式乘法与因式分解有什么关系?
是互为相反的变形,即
想一想
和
积
例1 下列从左到右的变形中是因式分解的有( )
①x2-y2-1=(x+y)(x-y)-1;②x3+x=x(x2+1);③(x-y)2=x2-2xy+y2;④x2-9y2=(x+3y)(x-3y).
A.1个 B.2个 C.3个 D.4个
范例应用
B
结果为积形式.
1.分清题目要求是整式乘法还是因式分解;
2.因式分解的结果必须是乘积形式.
方法总结:因式分解与整式乘法是相反方向的变形,即互逆运算,二者是一个式子的不同表现形式.因式分解的右边是两个或几个因式积的形式,整式乘法的右边是多项式的形式.
即时测评
下列等式从左到右的变形,属于因式分解的是( )
A.(a+b)(a﹣b)=a2﹣b2
B.x2+2x﹣1=(x+1)(x﹣1)+2x
C.m2﹣4m+4=m(m﹣4)+4
D.﹣6x2+3x=﹣3x(2x﹣1)
D
任务二 提取公因式法
活动1
2.根据上题的启发,试一试因式分解:
逆用乘法分配律
1.请用简便的方法计算 365 × 37 + 365 × 63,
思考在简便运算中运用了什么运算法则?
= 365 × (37 + 63)
= 365 × 100
= 36500.
ma+mb.
365 × 37 + 365 × 63
ma+mb
=ma+mb
=m(a+b)
365×37+365×63
=365×(37+63)
=365×100
=36500
逆用乘法分配律
公因式 m
多项式中各项都含有的公共因式,
叫作这个多项式各项的公因式
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫作提公因式法.
( a+b+c )
pa+ pb +pc
p
=
pa+pb+pc
相同因式p
范例应用
公因式是m
【例2】分解因式:
(1)mx2+my2; (2)3x2-4xy2+x.
解:(1)mx2+my2
=m x2+m y2
=m(x2-y2).
(2)3x2-4xy2+x
=x 3x-x 4y2+x 1
=x(3x-4y2+1).
公因式是x
即时测评
把下列各式分解因式:
(1)ax+ay;
(2)a2b2+ab-a;
(3)21xy-14xz+x2;
(4)2mn-4m2n+m.
解:(1)ax+ay=a(x+y).
(2)a2b2+ab-a=a(ab2+b-1).
(3)21xy-14xz+x2=x(21y-14z+x).
(4)2mn-4m2n+m=m(2n-4mn+1).
当堂达标
叁
当堂达标
1. 下列由左到右的变形,属于因式分解的是( )
A.(x+2)(x﹣2)=x2﹣4
B.x2﹣4=(x+2)(x﹣2)
C.x2﹣4+3x=(x+2)(x﹣2)+3x
D.x2+4x﹣2=x(x+4)﹣2
2.下列分解因式正确的是( )
(A)2x2-xy-x=x(x-y-1)
(B)xy2+2xy-3y=y(xy+2x+3)
(C)x2-xy=x(x-y)
(D)x2-x-3=x(x-1)-3
B
C
3.在下列等式中,从左到右的变形是因式分解的有 ,不是的,请说明为什么?
①
②
③
④
⑤
⑥
③
⑥
am+bm+c=m(a+b)+c
24x2y=3x ·8xy
x2-1=(x+1)(x-1)
(2x+1)2=4x2+4x+1
x2+x=x2(1+ )
2x+4y+6z=2(x+2y+3z)
最后不是积的运算
因式分解的对象是多项式,
是整式乘法
每个因式必须是整式
4.把下列各式分解因式:
(1)a2+5a;
(2)x2﹣2x;
(3)a2+ab﹣a;
(4)4x2+6xy-x.
解:(1)a2+5a=a(a+5).
(2)x2﹣2x=x(x﹣2).
(3)a2+ab﹣a=a(a+b﹣1).
(4)4x2+6xy-x=x(4x+6y-1).
5.利用因式分解进行简便计算:
(1)23.7×1.6+8.4×23.7;
(2)34.3×17.1+82.5×17.1-268×1.71+171.
解:(1)23.7×1.6+8.4×23.7
=23.7×(1.6+8.4)
=23.7×10
=237.
(2)34.3×17.1+82.5×17.1-268×1.71+171
=34.3×17.1+82.5×17.1-26.8×17.1+10×17.1
=17.1×(34.3+82.5-26.8+10)
=17.1×100
=1 710.
课堂小结
肆
课堂小结
1. 因式分解与整式乘法是一个互逆过程,即:
因式分解
整式乘法
几个整式相乘
一个多项式
提公因式法
分两步:
第一步找公因式;第二步提公因式
2.
课后作业
基础题:1.课后习题 第 1,2题。
提高题:2.请学有余力的同学完成课后习题第3题
谢
谢
同课章节目录
