17.1 用提公因式法分解因式 第2课时 用提公因式法分解较复杂的多项式 课件(共22张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 17.1 用提公因式法分解因式 第2课时 用提公因式法分解较复杂的多项式 课件(共22张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1012.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 23:02:45 | ||
图片预览








文档简介
(共22张PPT)
第17章 因式分解
17.1 用提公因式法分解因式
第2课时
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
2.什么是公因式?什么是提公因式法?
多项式中各项都含有的公共因式,叫作这个多项式各项的公因式.
1.什么是因式分解?因式分解与整式乘法有什么关系?
把一个多项式化成了几个整式的积的形式,像这样的式子变形叫作这个多项式的因式分解,也叫作把这个多项式分解因式.
互逆运算
把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫作提公因式法.
新知初探
贰
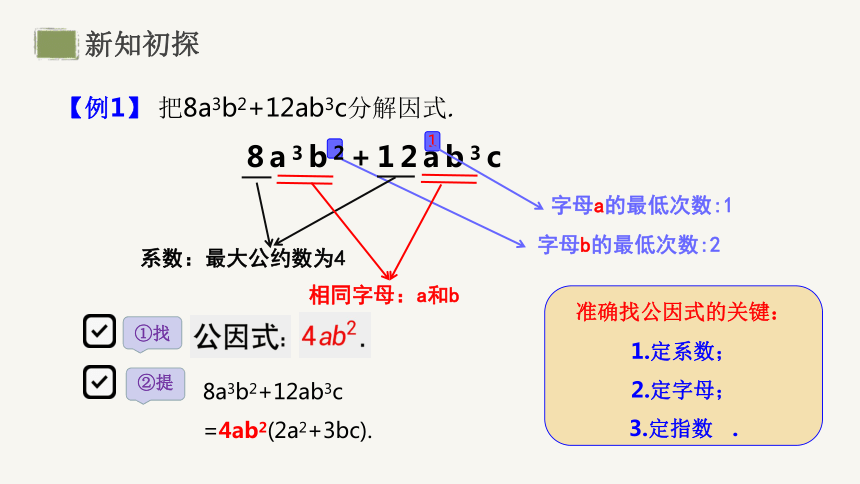
字母b的最低次数:2
8a3b2+12ab3c
新知初探
【例1】 把8a3b2+12ab3c分解因式.
系数:最大公约数为4
相同字母:a和b
1
字母a的最低次数:1
准确找公因式的关键:
1.定系数;
2.定字母;
3.定指数 .
②提
①找
8a3b2+12ab3c
=4ab2(2a2+3bc).
解:8a3b2+12ab3c
=4ab2 2a2+4ab2 3bc
=4ab2(2a2+3bc).
【例1】 把8a3b2+12ab3c分解因式.
再无公因式.
如果提出公因式4ab,另一个因式是否还有公因式
解:8a3b2+12ab3c
=4ab2 2a2+4ab2 3bc
=4ab2(2a2+3bc).
【例1】 把8a3b2+12ab3c分解因式.
多项式提取公因式后剩余的项不再含有公因式
在提取公因式时应该注意什么?
即时测评
分解因式
(1)-5x+5xy; (2)2a2b-4ab2;
(3)9x2-6xy+3xz; (4)6m2n-15n2m+30m2n2.
解:(1)-5x+5xy=-5x(1-y).
(2)2a2b-4ab2=2ab(a-2b).
(3)9x2-6xy+3xz=3x(3x-2y+z).
(4)6m2n-15n2m+30m2n2=3mn(2m-5n+10mn).
【例2】把2a(b+c)-3(b+c)分解因式.
2a(b+c)-3(b+c)
1.定系数:各项系数的最大公约数为1
2.定字母:各项中公共的字母因式为(b+c)
3.定指数:相同字母因式的最低次数为1
①找
(b+c)
②提
2a(b+c)-3(b+c)
=(b+c) (2a-3)
如何验证分解结果是否正确?
4(a-b)3+8(b-a)2
【例3】把4(a-b)3+8(b-a)2分解因式.
1.定系数:各项系数的最大公约数为4
2.定字母:各项中公共的字母因式为(a-b)
3.定指数:相同字母因式的最低次数为2
①找
4(a-b)2
②提
4(a-b)3+8(b-a)2
=4(a-b)2(a-b+2).
(a-b)2
【例3】把4(a-b)3+8(b-a)2分解因式.
解:4(a-b)3+8(b-a)2
=4(a-b)3+8(a-b)2
=4(a-b)2 (a-b)+4(a-b)2 2
=4(a-b)2(a-b+2).
能把(a-b)转化成(b-a)吗?此时怎样提公因式
提取公因式分解因式的技巧:
①当公因式是多项式时,把多项式看成一个整体提取公因式;
②分解因式分解到不能分解为止;
③某一项全部提取后,不要漏掉“1”;
④首项有负号常提负号;
⑤检查因式分解的结果是否正确,可用整式的乘法验证.
归纳总结
即时测评
因式分解:
(1)2a(b+c)-5(b+c). (2)2a(a+b)-(a+b)2.
(3)3m(b-c)-2n(c-b). (4)m(a-b)2-n(b-a).
解:(1) 2a(b+c)-5(b+c)=(b+c)(2a-5).
(2) 2a(a+b)-(a+b)2=(a+b)(2a-a-b)=(a+b)(a-b).
(3) 3m(b-c)-2n(c-b)=3m(b-c)+2n(b-c)=(b-c) (3m+2n).
(4) m(a-b)2-n(b-a)=m(a-b)2+n(a-b)=(a-b)(ma-mb+n).
当堂达标
叁
当堂达标
1. 把多项式2x3y-x2y2-6x2y分解因式时,应提取的公因式为( )
A.x2y B.xy2 C.2x3y D.xy
2.下列因式分解正确的是( )
A.2a2-a=2a(a-1) B.-a2-2ab=-a(a-2b)
C.-3a+3b=-3(a+b) D.a2+3ab=a(a+3b)
3.因式分解:
(1)6x2-3x= .
(2) 2a(b+c)-3(b+c)= .
A
D
3x(2x-1)
(b+c)(2a-3)
4.因式分解:
(1)a3b2+a2b2-ab;
(2)21xy-14xz+35x2;
(3)12a(x2+y2)-18b(x2+y2);
(4)(2a+b)(3a-2b)-4a(2a+b).
解:(1)原式=ab(a2b+ab-1);
(2)原式=7x(3y-2z+5x);
(3)原式=6(x2+y2)(2a-3b);
(4)原式=(2a+b)(3a-2b-4a)=(2a+b)(-a-2b)
=-(2a+b)(a+2b).
5.先分解因式,再计算求值.
(1)3(2x-1)2+(2x-1)(2-6x),其中x=1.
解:3(2x-1)2+(2x-1)(2-6x),
=(2x-1)(6x-3+2-6x),
=-(2x-1).
当x=1时,原式=-(2×1-1)=-1;
课堂小结
肆
课堂小结
提公因式法
确定公因式
提公因式并确定另外一个因式
把多项式写成这两个因式的积的形式
课后作业
基础题:1.课后习题 第 4,5题。
提高题:2.请学有余力的同学完成课后习题第8题
谢
谢
第17章 因式分解
17.1 用提公因式法分解因式
第2课时
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
2.什么是公因式?什么是提公因式法?
多项式中各项都含有的公共因式,叫作这个多项式各项的公因式.
1.什么是因式分解?因式分解与整式乘法有什么关系?
把一个多项式化成了几个整式的积的形式,像这样的式子变形叫作这个多项式的因式分解,也叫作把这个多项式分解因式.
互逆运算
把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫作提公因式法.
新知初探
贰
字母b的最低次数:2
8a3b2+12ab3c
新知初探
【例1】 把8a3b2+12ab3c分解因式.
系数:最大公约数为4
相同字母:a和b
1
字母a的最低次数:1
准确找公因式的关键:
1.定系数;
2.定字母;
3.定指数 .
②提
①找
8a3b2+12ab3c
=4ab2(2a2+3bc).
解:8a3b2+12ab3c
=4ab2 2a2+4ab2 3bc
=4ab2(2a2+3bc).
【例1】 把8a3b2+12ab3c分解因式.
再无公因式.
如果提出公因式4ab,另一个因式是否还有公因式
解:8a3b2+12ab3c
=4ab2 2a2+4ab2 3bc
=4ab2(2a2+3bc).
【例1】 把8a3b2+12ab3c分解因式.
多项式提取公因式后剩余的项不再含有公因式
在提取公因式时应该注意什么?
即时测评
分解因式
(1)-5x+5xy; (2)2a2b-4ab2;
(3)9x2-6xy+3xz; (4)6m2n-15n2m+30m2n2.
解:(1)-5x+5xy=-5x(1-y).
(2)2a2b-4ab2=2ab(a-2b).
(3)9x2-6xy+3xz=3x(3x-2y+z).
(4)6m2n-15n2m+30m2n2=3mn(2m-5n+10mn).
【例2】把2a(b+c)-3(b+c)分解因式.
2a(b+c)-3(b+c)
1.定系数:各项系数的最大公约数为1
2.定字母:各项中公共的字母因式为(b+c)
3.定指数:相同字母因式的最低次数为1
①找
(b+c)
②提
2a(b+c)-3(b+c)
=(b+c) (2a-3)
如何验证分解结果是否正确?
4(a-b)3+8(b-a)2
【例3】把4(a-b)3+8(b-a)2分解因式.
1.定系数:各项系数的最大公约数为4
2.定字母:各项中公共的字母因式为(a-b)
3.定指数:相同字母因式的最低次数为2
①找
4(a-b)2
②提
4(a-b)3+8(b-a)2
=4(a-b)2(a-b+2).
(a-b)2
【例3】把4(a-b)3+8(b-a)2分解因式.
解:4(a-b)3+8(b-a)2
=4(a-b)3+8(a-b)2
=4(a-b)2 (a-b)+4(a-b)2 2
=4(a-b)2(a-b+2).
能把(a-b)转化成(b-a)吗?此时怎样提公因式
提取公因式分解因式的技巧:
①当公因式是多项式时,把多项式看成一个整体提取公因式;
②分解因式分解到不能分解为止;
③某一项全部提取后,不要漏掉“1”;
④首项有负号常提负号;
⑤检查因式分解的结果是否正确,可用整式的乘法验证.
归纳总结
即时测评
因式分解:
(1)2a(b+c)-5(b+c). (2)2a(a+b)-(a+b)2.
(3)3m(b-c)-2n(c-b). (4)m(a-b)2-n(b-a).
解:(1) 2a(b+c)-5(b+c)=(b+c)(2a-5).
(2) 2a(a+b)-(a+b)2=(a+b)(2a-a-b)=(a+b)(a-b).
(3) 3m(b-c)-2n(c-b)=3m(b-c)+2n(b-c)=(b-c) (3m+2n).
(4) m(a-b)2-n(b-a)=m(a-b)2+n(a-b)=(a-b)(ma-mb+n).
当堂达标
叁
当堂达标
1. 把多项式2x3y-x2y2-6x2y分解因式时,应提取的公因式为( )
A.x2y B.xy2 C.2x3y D.xy
2.下列因式分解正确的是( )
A.2a2-a=2a(a-1) B.-a2-2ab=-a(a-2b)
C.-3a+3b=-3(a+b) D.a2+3ab=a(a+3b)
3.因式分解:
(1)6x2-3x= .
(2) 2a(b+c)-3(b+c)= .
A
D
3x(2x-1)
(b+c)(2a-3)
4.因式分解:
(1)a3b2+a2b2-ab;
(2)21xy-14xz+35x2;
(3)12a(x2+y2)-18b(x2+y2);
(4)(2a+b)(3a-2b)-4a(2a+b).
解:(1)原式=ab(a2b+ab-1);
(2)原式=7x(3y-2z+5x);
(3)原式=6(x2+y2)(2a-3b);
(4)原式=(2a+b)(3a-2b-4a)=(2a+b)(-a-2b)
=-(2a+b)(a+2b).
5.先分解因式,再计算求值.
(1)3(2x-1)2+(2x-1)(2-6x),其中x=1.
解:3(2x-1)2+(2x-1)(2-6x),
=(2x-1)(6x-3+2-6x),
=-(2x-1).
当x=1时,原式=-(2×1-1)=-1;
课堂小结
肆
课堂小结
提公因式法
确定公因式
提公因式并确定另外一个因式
把多项式写成这两个因式的积的形式
课后作业
基础题:1.课后习题 第 4,5题。
提高题:2.请学有余力的同学完成课后习题第8题
谢
谢
同课章节目录
