第13章 三角形 数学活动 课件(共23张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 第13章 三角形 数学活动 课件(共23张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 23:05:05 | ||
图片预览







文档简介
(共23张PPT)
第13章 三角形
数学活动
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
1. 什么是三角形?什么是等边三角形?
三条线段首尾顺次相接所组成的图形叫作三角形.
三边都相等的三角形是等边三角形.
用更多的磁力棒如何搭等边三角形呢?
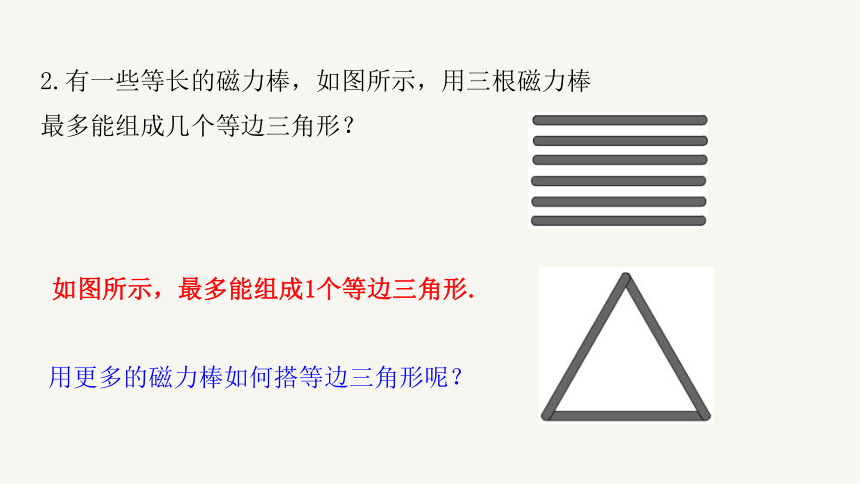
2.有一些等长的磁力棒,如图所示,用三根磁力棒最多能组成几个等边三角形?
如图所示,最多能组成1个等边三角形.
新知初探
贰
新知初探
如图所示,共能摆出4个等边三角形.
活动1
搭等边三角形
1.现在有6根磁力棒,最多能组成多少个等边三角形?动手试一试,并与同学们交流,注意可以考虑立体图形.
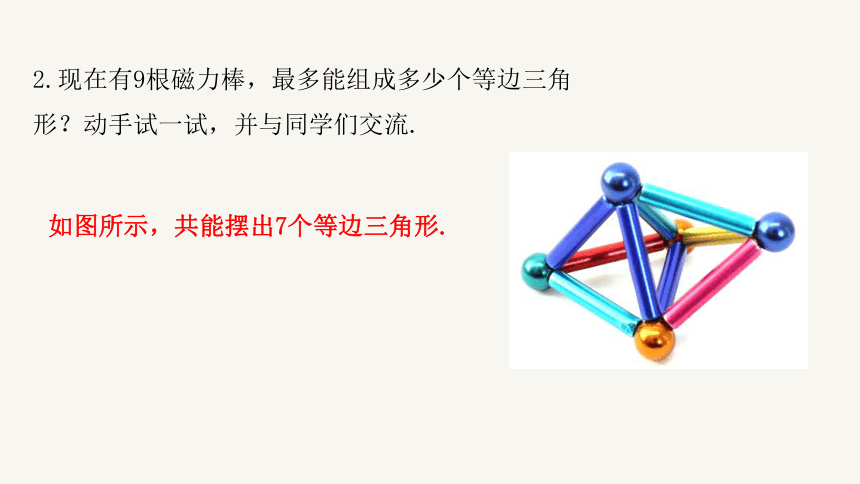
如图所示,共能摆出7个等边三角形.
2.现在有9根磁力棒,最多能组成多少个等边三角形?动手试一试,并与同学们交流.
活动2
多边形的三角剖分
三条线段首尾顺次相接组成三角形,类似地,多条线段首尾顺次相接就组成多边形.
问题1 三角形与多边形是什么关系?
三角形是多边形的一种,是最简单的多边形.
把一个多边形用连接它的不相邻顶点的线段(这些线段不在多边形内部相交)划分为若干个三角形,叫作多边形的三角剖分.
问题2 如图所示,是一个七边形,你能对它进
行三角剖分吗?能分成多少个三角形
如图所示:
七边形三角剖分能剖分出5个三角形.
归纳总结:对n边形进行三角剖分,能剖分出(n-2)个三角形.
问题3 分别将一个四边形、五边形、六边形
进行三角剖分,分别能剖分出多少个三角形?
四边形能剖分出2个三角形,五边形能剖分出3个三角形,六边形能剖分出4个三角形.
如图所示,共有2种剖分方法.
问题4 将一个四边形进行三角剖分,你有多少
种剖分方法?分别画一下.
将一个五边形进行三角剖分,你有多少
种剖分方法?分别画一下.
如图所示,共有5种剖分方法.
1751年,瑞士数学家欧拉(Euler.1707--1783)向德
国—俄国数学家哥德巴赫(Goldbach,1690-1764)提出了一个n边形的三角剖分有多少种不同方法的问题,并归纳得出了n边形的不同三角剖分方法数(Dn)的公式。
后来数学家发现并证明:
当n≥3时, (D3=1).
欧拉
问题5 你能利用上述公式,验证你前面得到的结果吗?写出你的验证过程.
当n≥3时, (D3=1).
解:当n=3时, ,
因为D3=1,所以D4=2.
当n=4时, ,
因为D4=2,所以D5=5.
当n≥3时, (D3=1).
问题6 请你利用上述公式,计算六边形、七边形的三角剖分方法数.
解:当n=5时, ,
因为D5=5,所以D6=14.
当n=6时, ,
因为D6=14,所以D7=42.
当堂达标
叁
当堂达标
1. 用9根磁力棒来组成三角形,最多能组成多少个等边三角形( )
A.4 B.5 C.6 D.7
2.把一个n边形进行三角剖分,则这个n边形分割成6个三角形,则n的值是( )
(A)6 (B)7 (C)8 (D)9
D
C
3.根据n边形的不同三角剖分方法数(Dn)的公式:
请计算八边形的三角剖分方法数.
当n≥3时, (D3=1).
解:当n=7时, ,
因为D7=42,所以D8=132.
所以八边形的三角剖分方法数为132.
课堂小结
肆
课堂小结
(1)本节课主要学习了哪些知识 学习了哪些数学思想和方法
(2)本节课还有哪些疑惑 请同学们说一说.
课后作业
基础题:1.课后复习题 第 6,7题。
提高题:2.请学有余力的同学完成课后习题第12题
谢
谢
第13章 三角形
数学活动
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
1. 什么是三角形?什么是等边三角形?
三条线段首尾顺次相接所组成的图形叫作三角形.
三边都相等的三角形是等边三角形.
用更多的磁力棒如何搭等边三角形呢?
2.有一些等长的磁力棒,如图所示,用三根磁力棒最多能组成几个等边三角形?
如图所示,最多能组成1个等边三角形.
新知初探
贰
新知初探
如图所示,共能摆出4个等边三角形.
活动1
搭等边三角形
1.现在有6根磁力棒,最多能组成多少个等边三角形?动手试一试,并与同学们交流,注意可以考虑立体图形.
如图所示,共能摆出7个等边三角形.
2.现在有9根磁力棒,最多能组成多少个等边三角形?动手试一试,并与同学们交流.
活动2
多边形的三角剖分
三条线段首尾顺次相接组成三角形,类似地,多条线段首尾顺次相接就组成多边形.
问题1 三角形与多边形是什么关系?
三角形是多边形的一种,是最简单的多边形.
把一个多边形用连接它的不相邻顶点的线段(这些线段不在多边形内部相交)划分为若干个三角形,叫作多边形的三角剖分.
问题2 如图所示,是一个七边形,你能对它进
行三角剖分吗?能分成多少个三角形
如图所示:
七边形三角剖分能剖分出5个三角形.
归纳总结:对n边形进行三角剖分,能剖分出(n-2)个三角形.
问题3 分别将一个四边形、五边形、六边形
进行三角剖分,分别能剖分出多少个三角形?
四边形能剖分出2个三角形,五边形能剖分出3个三角形,六边形能剖分出4个三角形.
如图所示,共有2种剖分方法.
问题4 将一个四边形进行三角剖分,你有多少
种剖分方法?分别画一下.
将一个五边形进行三角剖分,你有多少
种剖分方法?分别画一下.
如图所示,共有5种剖分方法.
1751年,瑞士数学家欧拉(Euler.1707--1783)向德
国—俄国数学家哥德巴赫(Goldbach,1690-1764)提出了一个n边形的三角剖分有多少种不同方法的问题,并归纳得出了n边形的不同三角剖分方法数(Dn)的公式。
后来数学家发现并证明:
当n≥3时, (D3=1).
欧拉
问题5 你能利用上述公式,验证你前面得到的结果吗?写出你的验证过程.
当n≥3时, (D3=1).
解:当n=3时, ,
因为D3=1,所以D4=2.
当n=4时, ,
因为D4=2,所以D5=5.
当n≥3时, (D3=1).
问题6 请你利用上述公式,计算六边形、七边形的三角剖分方法数.
解:当n=5时, ,
因为D5=5,所以D6=14.
当n=6时, ,
因为D6=14,所以D7=42.
当堂达标
叁
当堂达标
1. 用9根磁力棒来组成三角形,最多能组成多少个等边三角形( )
A.4 B.5 C.6 D.7
2.把一个n边形进行三角剖分,则这个n边形分割成6个三角形,则n的值是( )
(A)6 (B)7 (C)8 (D)9
D
C
3.根据n边形的不同三角剖分方法数(Dn)的公式:
请计算八边形的三角剖分方法数.
当n≥3时, (D3=1).
解:当n=7时, ,
因为D7=42,所以D8=132.
所以八边形的三角剖分方法数为132.
课堂小结
肆
课堂小结
(1)本节课主要学习了哪些知识 学习了哪些数学思想和方法
(2)本节课还有哪些疑惑 请同学们说一说.
课后作业
基础题:1.课后复习题 第 6,7题。
提高题:2.请学有余力的同学完成课后习题第12题
谢
谢
同课章节目录
