陕西省西安市铁一中陆港初级中学、滨河中学2025届九年级下学期中考十模数学试卷(含详解)
文档属性
| 名称 | 陕西省西安市铁一中陆港初级中学、滨河中学2025届九年级下学期中考十模数学试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 271.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-08 07:21:54 | ||
图片预览



文档简介
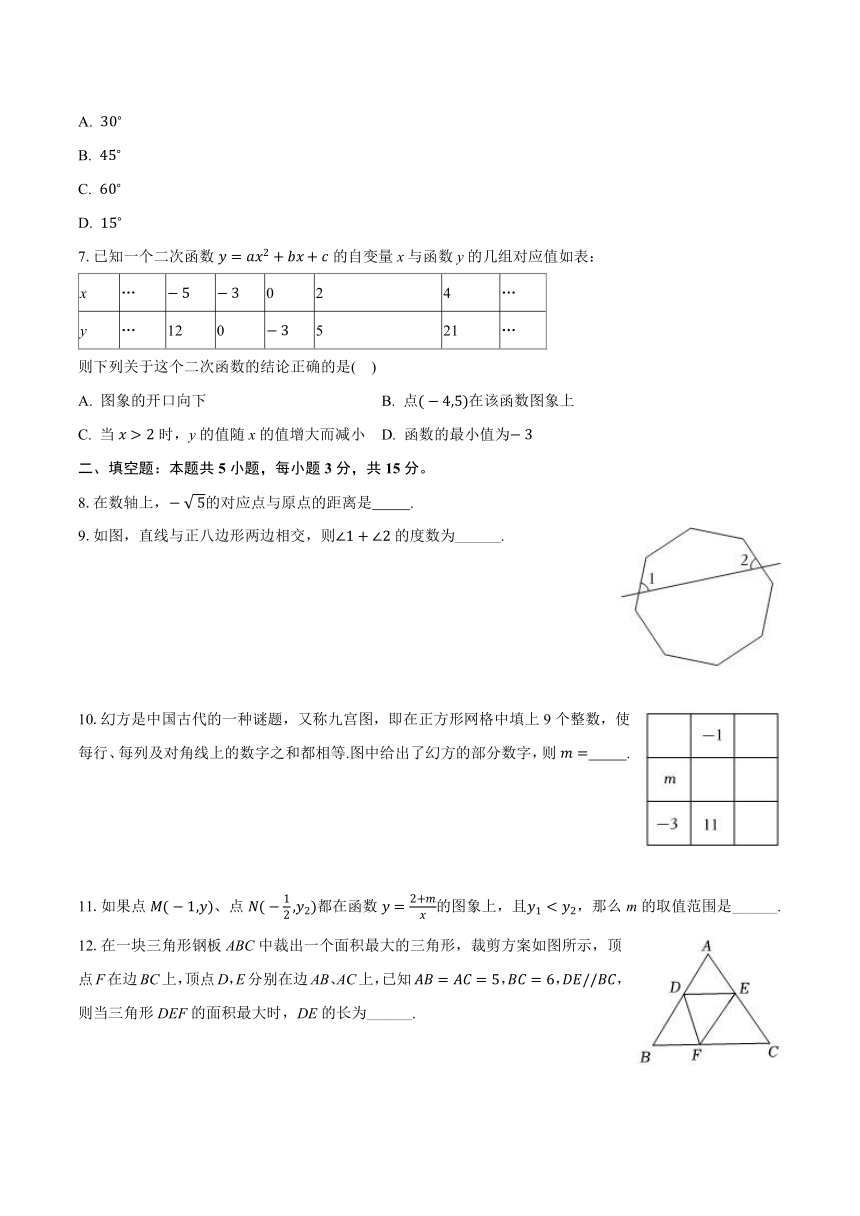
2025年陕西省西安市铁一中陆港初级中学、滨河中学中考数学十模试卷
一、选择题:本题共7小题,每小题3分,共21分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在、、0、1这四个数中,最小的数是( )
A. B. C. 0 D. 1
2.下列倡导节约的图案中,是轴对称图形的是( )
A. B. C. D.
3.若单项式和的积为,则ab的值为( )
A. 2 B. 30 C. D. 15
4.若正比例函数的图象在第二、四象限,则一次函数的图象大致是( )
A. B.
C. D.
5.如图,在中,D,E分别为AB,AC边的中点,,连接EF,交DC于点M,若,则MC的长为( )
A. 3
B. 4
C.
D.
6.如图,的内接四边形ABCD中,于点B,,连接DB,则的度数为( )
A.
B.
C.
D.
7.已知一个二次函数的自变量x与函数y的几组对应值如表:
x … 0 2 4 …
y … 12 0 5 21 …
则下列关于这个二次函数的结论正确的是( )
A. 图象的开口向下 B. 点在该函数图象上
C. 当时,y的值随x的值增大而减小 D. 函数的最小值为
二、填空题:本题共5小题,每小题3分,共15分。
8.在数轴上,的对应点与原点的距离是 .
9.如图,直线与正八边形两边相交,则的度数为______.
10.幻方是中国古代的一种谜题,又称九宫图,即在正方形网格中填上9个整数,使每行、每列及对角线上的数字之和都相等.图中给出了幻方的部分数字,则 .
11.如果点、点都在函数的图象上,且,那么m的取值范围是______.
12.在一块三角形钢板ABC中裁出一个面积最大的三角形,裁剪方案如图所示,顶点F在边BC上,顶点D,E分别在边AB、AC上,已知,,,则当三角形DEF的面积最大时,DE的长为______.
三、解答题:本题共13小题,共84分。解答应写出文字说明,证明过程或演算步骤。
13.本小题5分
计算:
14.本小题5分
解不等式组
15.本小题5分
先化简:,再从,,1,3中选取一个使原式有意义的数代入求值.
16.本小题5分
如图,请用尺规作图法,在矩形ABCD内部求作一点P,使,且保留作图痕迹,不写作法
17.本小题5分
如图,,过点D作,垂足为M,E在BC边上,,求证:
18.本小题5分
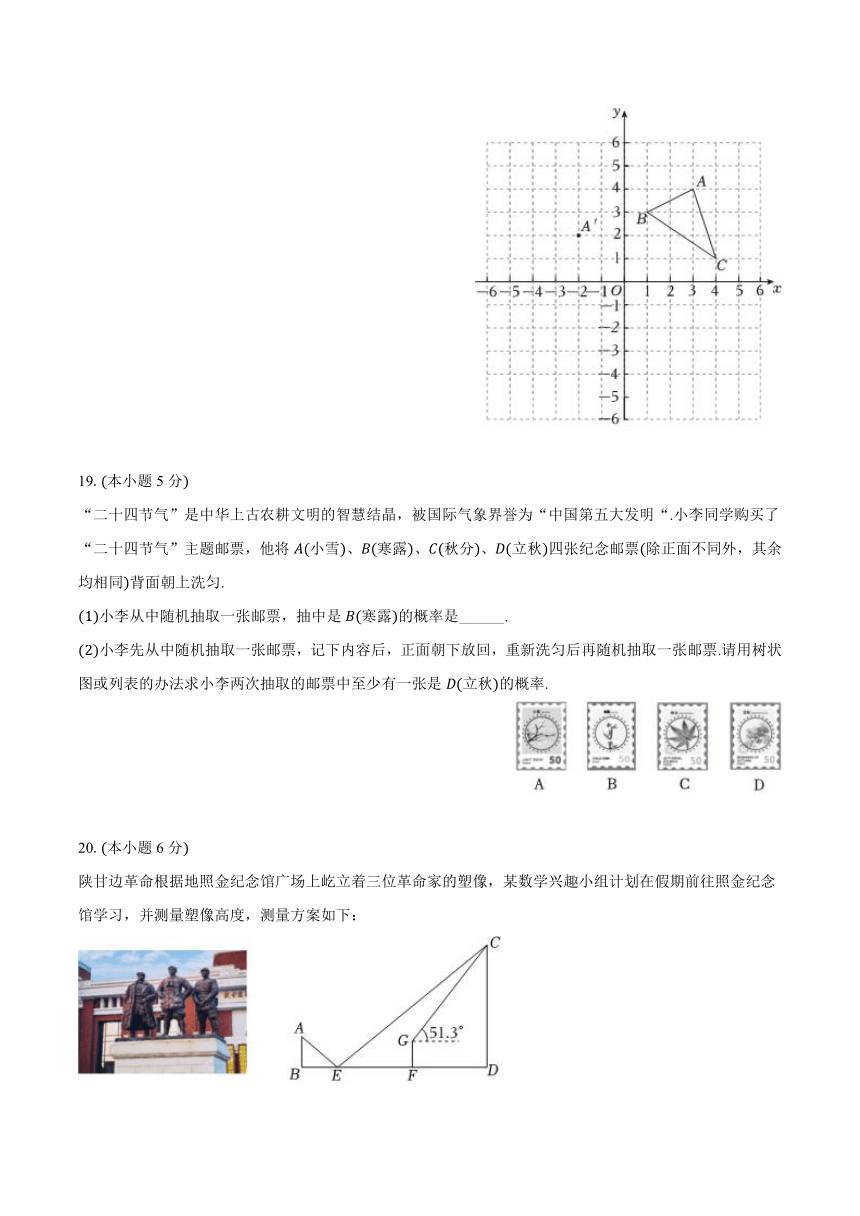
如图,在平面直角坐标系xOy中,的三个顶点的位置如图所示,点的坐标是现将平移,使点A与点重合,点B、C的对应点分别是点、
请画出平移后的,并写出点的坐标______;
点P是内的一点,当平移到后,若点P的对应点的坐标为,则点P的坐标为______.
19.本小题5分
“二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明“.小李同学购买了“二十四节气”主题邮票,他将小雪、寒露、秋分、立秋四张纪念邮票除正面不同外,其余均相同背面朝上洗匀.
小李从中随机抽取一张邮票,抽中是寒露的概率是______.
小李先从中随机抽取一张邮票,记下内容后,正面朝下放回,重新洗匀后再随机抽取一张邮票.请用树状图或列表的办法求小李两次抽取的邮票中至少有一张是立秋的概率.
20.本小题6分
陕甘边革命根据地照金纪念馆广场上屹立着三位革命家的塑像,某数学兴趣小组计划在假期前往照金纪念馆学习,并测量塑像高度,测量方案如下:
如图,点B、E、F、D四点在同一条直线上,先在点E处放置平面镜,小明从点E处沿DE方向移动到点B处,视线刚好在平面镜内看到塑像顶端C的像,再在点F处安装测倾器GF,测得塑像顶端C的仰角为测得眼睛离地面高度米,米,米,米,,,求塑像CD的高度平面镜大小忽略不计,参考数据:,,
21.本小题6分
甲、乙两车分别从A地将一批物品运往B地,再返回A地,两车离A地的距离千米随时间小时变化的图象如图所示,乙车到达B地后以25千米/小时的速度返回.
甲车出发多长时间后被乙车追上?
甲车与乙车在距离A地多远处迎面相遇?
22.本小题7分
为进一步落实“双减”政策,某校对七、八年级学生某天“书面作业”的时间单位:小时进行了随机抽样调查,共获得220名七、八年级学生“书面作业”时间数据,绘制成如下统计图表,请根拟图表中的信息回答下列问题.
类别 书面作业”的时间小时 频数七年级 频数八年级
A 15 10
B 40 25
C a 45
D 10 b
频数分布表中,______,______;
①补全条形统计图;
②七年级甲同学的“书面作业”时间是此次抽样调查中七年级所得数据的中位数,则甲同学的“书面作业”时间在哪个范围内;
“双减”政策规定初中生书面作业时间不超过90分钟,已知该校七年级学生有500人,八年级学生有600人,分别估计该校七、八年级学生“书面作业”的时间符合规定的人数.
23.本小题8分
如图,的内接四边形ABCD中,,AB是直径,过点C作的切线交AB的延长线于点P,延长DO交于点E,连接
求证:PE是的切线;
若,,求的半径.
24.本小题10分
如图,蔬菜大棚顶部AB段是抛物线的一部分,下方是长方形ABCD,已知长方形ABCD的长,宽,大棚顶部最高处P距离地面10m高,建立如图所示的平面直角坐标系.
求出大棚顶部所在抛物线的函数表达式;
若准备在大棚一侧开一扇正方形的活动门,如图阴影部分所示,方便天气好时打开透气,则这个正方形的边长为多少?
25.本小题12分
【问题提出】
如图1,在由线段AB,BC,CD与孤AD围成的封闭图形中,,,,,E是弧AD上任意一点,若弧AD的半径为2,则面积的最小值为______;
【问题解决】
如图2,四边形ABCD是一块空地,经测量,,,,规划部门在四边形ABCD内一点E处建一座凉亭,凉亭四周修建四条观赏步道步道宽度忽略不计,分别为AE,BE,CE,DE,且步道将空地分为四个区域,计划种植不同的花卉,其中区域种植牡丹,牡丹比较昂贵,种植成本高,为节约成本,要求面积尽可能的小.请问:是否存在符合要求的三角形区域?若存在,求出面积的最小值;若不存在,请说明理由结果精确到整数;参考数据:,,
答案和解析
1.A
解:,
最小的数是
故选:
2.C
解:A,B,D选项中的图形都不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形.
C选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形.
故选:
3.D
解:,
,,
解得,,
,
故选:
4.C
解:正比例函数的图象经过第二、四象限,
,
一次函数的图象经过一、二、四象限,
故选:
5.B
解:,
,
,E分别为AB,AC边的中点,
,且,
,
,
又,
,
故选:
6.B
解:连接AC,
于点B,
,
是等腰直角三角形,
,
故选:
7.B
解:设抛物线解析式为,
将、、代入得:,
解得,
所以解析式为,
则抛物线开口向上,
当时,,即在该函数图象上,
当时,y的值随x的值增大而减小,函数的最小值为,
故选:
8.
解:在数轴上,的对应点与原点的距离是,
故答案为:
9.
解:正八边形的内角和为
,
正八边形的每个内角的度数为,
五边形的内角和为
,
故答案为:
10.15
解:设第一行第三列的方格中的数字为a,如图所示,
因为每行及对角线上的数字之和都相等,
所以,
解得:
因为每行、每列上的数字之和都相等,
所以,
解得:
故答案为:
11.
解:点、点都在函数的图象上,且,
,
,
故答案为:
12.3
解:如图,过点A作交BC于点G,交DE于点
,
∽,∽,
,,
,
,,
,
在中利用勾股定理,得,
设,则,
,
,
,
当时,最大,
故答案为:
13.
解:原式
14.解:,
解①得:,
解②得:,
故不等式组的解为:
15.解:原式
,
,,,
,3,
当时,原式
16.见解析.
解:如图,点P,点即为所求.
17.证明见解答过程.
证明:,,
四边形BCDM是矩形,
,
,
,
在和中,
,
,
18.解:平移后的如图所示:
解:点的坐标是,点A的坐标是,
平移方向是先向左平移5个单位长度,再向下平移2个单位长度,
点B的坐标是,点C的坐标是,
点的坐标是,点的坐标是,
平移后的如图所示:
由得:平移方向是先向左平移5个单位长度,再向下平移2个单位长度,
点P的对应点的坐标为,
点P的坐标为,
故答案为;
19.;
解:小李从中随机抽取一张邮票,抽中是寒露的概率是
故答案为:;
画树状图如下:
共有16种等可能的结果,其中小李两次抽取的邮票中至少有一张是立秋的结果有:AD,BD,CD,DA,DB,DC,DD,共7种,
小李两次抽取的邮票中至少有一张是立秋的概率为
20.塑像CD的高度约为米.
解:过点G作,垂足为H,
由题意得:,米,,
设米,
米,
米,
在中,,
米,
米,
,,
,
∽,
,
,
解得:,
经检验:是原方程的根,
米,
塑像CD的高度约为米.
21.1小时;
40千米.
甲车的速度为千米/小时,
小时
答:甲车出发1小时后被乙车追上.
当时,甲车离A地的距离千米与时间小时的函数关系式为,
乙车从A地到B地过程中的速度为千米/小时,
小时,
当时,乙车到达B地,
则乙车返回A地过程中离A地的距离千米与时间小时的函数关系式为,
当两车迎面相遇时,得,
解得
答:甲车与乙车在距离A地40千米处迎面相遇.
22.35,40;
①详见解答;
②中位数落在“B组”,在范围内;
估计该校七、八年级学生“书面作业”的时间符合规定的人数有850人.
由于样本中八年级学生学习时间在“A组”所对应的圆心角为,即占调查人数的,而在“A组”的有10人,
所以八年级所调查的学生人数为人,
因此七年级的调查人数为人,
所以人,人,
故答案为:35,40;
①补全条形统计图如下:
②七年级的样本容量是100,因此中位数是将这100名学生的“书面作业”从小到大排列后,则第50位,第51位数据的平均数,
因此中位数落在“B组”,
甲同学的“书面作业”时间在范围内;
,
人,
答:估计该校七、八年级学生“书面作业”的时间符合规定的人数有850人.
23.见解析;
的半径为
证明:连接OC,
是的切线,
,
,
,
,
,
,
在与中,
,
≌,
,
是的半径,
是的切线;
解:连接CE,
则,
,
,
是的直径,
,
∽,
,
,
,
即的半径为
24.抛物线的函数表达式为;
这个正方形的边长为,
由题意得:A的坐标为,顶点P的坐标为,
设,
把代入中得:
,
解得:,
抛物线的函数表达式为;
如图:
设,则,
点,
,
,
解得:,舍去,
,
这个正方形的边长为,
25.8;
设弧AD的圆心为O,过O作,交弧AD于点E,此时的面积最小,
,
面积的最小值,
故答案为:8;
根据题意,如图所示,
,
在AB为直径的上运动,且,
连接OD,作,,
,
,
,,
,
,
,
,
当HE最小时,的面积最小,
当H、E、O三点共线时,DC上的高最小,
此时,
,
答:面积的最小值为
一、选择题:本题共7小题,每小题3分,共21分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在、、0、1这四个数中,最小的数是( )
A. B. C. 0 D. 1
2.下列倡导节约的图案中,是轴对称图形的是( )
A. B. C. D.
3.若单项式和的积为,则ab的值为( )
A. 2 B. 30 C. D. 15
4.若正比例函数的图象在第二、四象限,则一次函数的图象大致是( )
A. B.
C. D.
5.如图,在中,D,E分别为AB,AC边的中点,,连接EF,交DC于点M,若,则MC的长为( )
A. 3
B. 4
C.
D.
6.如图,的内接四边形ABCD中,于点B,,连接DB,则的度数为( )
A.
B.
C.
D.
7.已知一个二次函数的自变量x与函数y的几组对应值如表:
x … 0 2 4 …
y … 12 0 5 21 …
则下列关于这个二次函数的结论正确的是( )
A. 图象的开口向下 B. 点在该函数图象上
C. 当时,y的值随x的值增大而减小 D. 函数的最小值为
二、填空题:本题共5小题,每小题3分,共15分。
8.在数轴上,的对应点与原点的距离是 .
9.如图,直线与正八边形两边相交,则的度数为______.
10.幻方是中国古代的一种谜题,又称九宫图,即在正方形网格中填上9个整数,使每行、每列及对角线上的数字之和都相等.图中给出了幻方的部分数字,则 .
11.如果点、点都在函数的图象上,且,那么m的取值范围是______.
12.在一块三角形钢板ABC中裁出一个面积最大的三角形,裁剪方案如图所示,顶点F在边BC上,顶点D,E分别在边AB、AC上,已知,,,则当三角形DEF的面积最大时,DE的长为______.
三、解答题:本题共13小题,共84分。解答应写出文字说明,证明过程或演算步骤。
13.本小题5分
计算:
14.本小题5分
解不等式组
15.本小题5分
先化简:,再从,,1,3中选取一个使原式有意义的数代入求值.
16.本小题5分
如图,请用尺规作图法,在矩形ABCD内部求作一点P,使,且保留作图痕迹,不写作法
17.本小题5分
如图,,过点D作,垂足为M,E在BC边上,,求证:
18.本小题5分
如图,在平面直角坐标系xOy中,的三个顶点的位置如图所示,点的坐标是现将平移,使点A与点重合,点B、C的对应点分别是点、
请画出平移后的,并写出点的坐标______;
点P是内的一点,当平移到后,若点P的对应点的坐标为,则点P的坐标为______.
19.本小题5分
“二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明“.小李同学购买了“二十四节气”主题邮票,他将小雪、寒露、秋分、立秋四张纪念邮票除正面不同外,其余均相同背面朝上洗匀.
小李从中随机抽取一张邮票,抽中是寒露的概率是______.
小李先从中随机抽取一张邮票,记下内容后,正面朝下放回,重新洗匀后再随机抽取一张邮票.请用树状图或列表的办法求小李两次抽取的邮票中至少有一张是立秋的概率.
20.本小题6分
陕甘边革命根据地照金纪念馆广场上屹立着三位革命家的塑像,某数学兴趣小组计划在假期前往照金纪念馆学习,并测量塑像高度,测量方案如下:
如图,点B、E、F、D四点在同一条直线上,先在点E处放置平面镜,小明从点E处沿DE方向移动到点B处,视线刚好在平面镜内看到塑像顶端C的像,再在点F处安装测倾器GF,测得塑像顶端C的仰角为测得眼睛离地面高度米,米,米,米,,,求塑像CD的高度平面镜大小忽略不计,参考数据:,,
21.本小题6分
甲、乙两车分别从A地将一批物品运往B地,再返回A地,两车离A地的距离千米随时间小时变化的图象如图所示,乙车到达B地后以25千米/小时的速度返回.
甲车出发多长时间后被乙车追上?
甲车与乙车在距离A地多远处迎面相遇?
22.本小题7分
为进一步落实“双减”政策,某校对七、八年级学生某天“书面作业”的时间单位:小时进行了随机抽样调查,共获得220名七、八年级学生“书面作业”时间数据,绘制成如下统计图表,请根拟图表中的信息回答下列问题.
类别 书面作业”的时间小时 频数七年级 频数八年级
A 15 10
B 40 25
C a 45
D 10 b
频数分布表中,______,______;
①补全条形统计图;
②七年级甲同学的“书面作业”时间是此次抽样调查中七年级所得数据的中位数,则甲同学的“书面作业”时间在哪个范围内;
“双减”政策规定初中生书面作业时间不超过90分钟,已知该校七年级学生有500人,八年级学生有600人,分别估计该校七、八年级学生“书面作业”的时间符合规定的人数.
23.本小题8分
如图,的内接四边形ABCD中,,AB是直径,过点C作的切线交AB的延长线于点P,延长DO交于点E,连接
求证:PE是的切线;
若,,求的半径.
24.本小题10分
如图,蔬菜大棚顶部AB段是抛物线的一部分,下方是长方形ABCD,已知长方形ABCD的长,宽,大棚顶部最高处P距离地面10m高,建立如图所示的平面直角坐标系.
求出大棚顶部所在抛物线的函数表达式;
若准备在大棚一侧开一扇正方形的活动门,如图阴影部分所示,方便天气好时打开透气,则这个正方形的边长为多少?
25.本小题12分
【问题提出】
如图1,在由线段AB,BC,CD与孤AD围成的封闭图形中,,,,,E是弧AD上任意一点,若弧AD的半径为2,则面积的最小值为______;
【问题解决】
如图2,四边形ABCD是一块空地,经测量,,,,规划部门在四边形ABCD内一点E处建一座凉亭,凉亭四周修建四条观赏步道步道宽度忽略不计,分别为AE,BE,CE,DE,且步道将空地分为四个区域,计划种植不同的花卉,其中区域种植牡丹,牡丹比较昂贵,种植成本高,为节约成本,要求面积尽可能的小.请问:是否存在符合要求的三角形区域?若存在,求出面积的最小值;若不存在,请说明理由结果精确到整数;参考数据:,,
答案和解析
1.A
解:,
最小的数是
故选:
2.C
解:A,B,D选项中的图形都不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形.
C选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形.
故选:
3.D
解:,
,,
解得,,
,
故选:
4.C
解:正比例函数的图象经过第二、四象限,
,
一次函数的图象经过一、二、四象限,
故选:
5.B
解:,
,
,E分别为AB,AC边的中点,
,且,
,
,
又,
,
故选:
6.B
解:连接AC,
于点B,
,
是等腰直角三角形,
,
故选:
7.B
解:设抛物线解析式为,
将、、代入得:,
解得,
所以解析式为,
则抛物线开口向上,
当时,,即在该函数图象上,
当时,y的值随x的值增大而减小,函数的最小值为,
故选:
8.
解:在数轴上,的对应点与原点的距离是,
故答案为:
9.
解:正八边形的内角和为
,
正八边形的每个内角的度数为,
五边形的内角和为
,
故答案为:
10.15
解:设第一行第三列的方格中的数字为a,如图所示,
因为每行及对角线上的数字之和都相等,
所以,
解得:
因为每行、每列上的数字之和都相等,
所以,
解得:
故答案为:
11.
解:点、点都在函数的图象上,且,
,
,
故答案为:
12.3
解:如图,过点A作交BC于点G,交DE于点
,
∽,∽,
,,
,
,,
,
在中利用勾股定理,得,
设,则,
,
,
,
当时,最大,
故答案为:
13.
解:原式
14.解:,
解①得:,
解②得:,
故不等式组的解为:
15.解:原式
,
,,,
,3,
当时,原式
16.见解析.
解:如图,点P,点即为所求.
17.证明见解答过程.
证明:,,
四边形BCDM是矩形,
,
,
,
在和中,
,
,
18.解:平移后的如图所示:
解:点的坐标是,点A的坐标是,
平移方向是先向左平移5个单位长度,再向下平移2个单位长度,
点B的坐标是,点C的坐标是,
点的坐标是,点的坐标是,
平移后的如图所示:
由得:平移方向是先向左平移5个单位长度,再向下平移2个单位长度,
点P的对应点的坐标为,
点P的坐标为,
故答案为;
19.;
解:小李从中随机抽取一张邮票,抽中是寒露的概率是
故答案为:;
画树状图如下:
共有16种等可能的结果,其中小李两次抽取的邮票中至少有一张是立秋的结果有:AD,BD,CD,DA,DB,DC,DD,共7种,
小李两次抽取的邮票中至少有一张是立秋的概率为
20.塑像CD的高度约为米.
解:过点G作,垂足为H,
由题意得:,米,,
设米,
米,
米,
在中,,
米,
米,
,,
,
∽,
,
,
解得:,
经检验:是原方程的根,
米,
塑像CD的高度约为米.
21.1小时;
40千米.
甲车的速度为千米/小时,
小时
答:甲车出发1小时后被乙车追上.
当时,甲车离A地的距离千米与时间小时的函数关系式为,
乙车从A地到B地过程中的速度为千米/小时,
小时,
当时,乙车到达B地,
则乙车返回A地过程中离A地的距离千米与时间小时的函数关系式为,
当两车迎面相遇时,得,
解得
答:甲车与乙车在距离A地40千米处迎面相遇.
22.35,40;
①详见解答;
②中位数落在“B组”,在范围内;
估计该校七、八年级学生“书面作业”的时间符合规定的人数有850人.
由于样本中八年级学生学习时间在“A组”所对应的圆心角为,即占调查人数的,而在“A组”的有10人,
所以八年级所调查的学生人数为人,
因此七年级的调查人数为人,
所以人,人,
故答案为:35,40;
①补全条形统计图如下:
②七年级的样本容量是100,因此中位数是将这100名学生的“书面作业”从小到大排列后,则第50位,第51位数据的平均数,
因此中位数落在“B组”,
甲同学的“书面作业”时间在范围内;
,
人,
答:估计该校七、八年级学生“书面作业”的时间符合规定的人数有850人.
23.见解析;
的半径为
证明:连接OC,
是的切线,
,
,
,
,
,
,
在与中,
,
≌,
,
是的半径,
是的切线;
解:连接CE,
则,
,
,
是的直径,
,
∽,
,
,
,
即的半径为
24.抛物线的函数表达式为;
这个正方形的边长为,
由题意得:A的坐标为,顶点P的坐标为,
设,
把代入中得:
,
解得:,
抛物线的函数表达式为;
如图:
设,则,
点,
,
,
解得:,舍去,
,
这个正方形的边长为,
25.8;
设弧AD的圆心为O,过O作,交弧AD于点E,此时的面积最小,
,
面积的最小值,
故答案为:8;
根据题意,如图所示,
,
在AB为直径的上运动,且,
连接OD,作,,
,
,
,,
,
,
,
,
当HE最小时,的面积最小,
当H、E、O三点共线时,DC上的高最小,
此时,
,
答:面积的最小值为
同课章节目录
