真题必读:专题一力与运动 命题区间1 力与物体的平衡--《高考快车道》2026版高考物理母题必读及衍生
文档属性
| 名称 | 真题必读:专题一力与运动 命题区间1 力与物体的平衡--《高考快车道》2026版高考物理母题必读及衍生 | 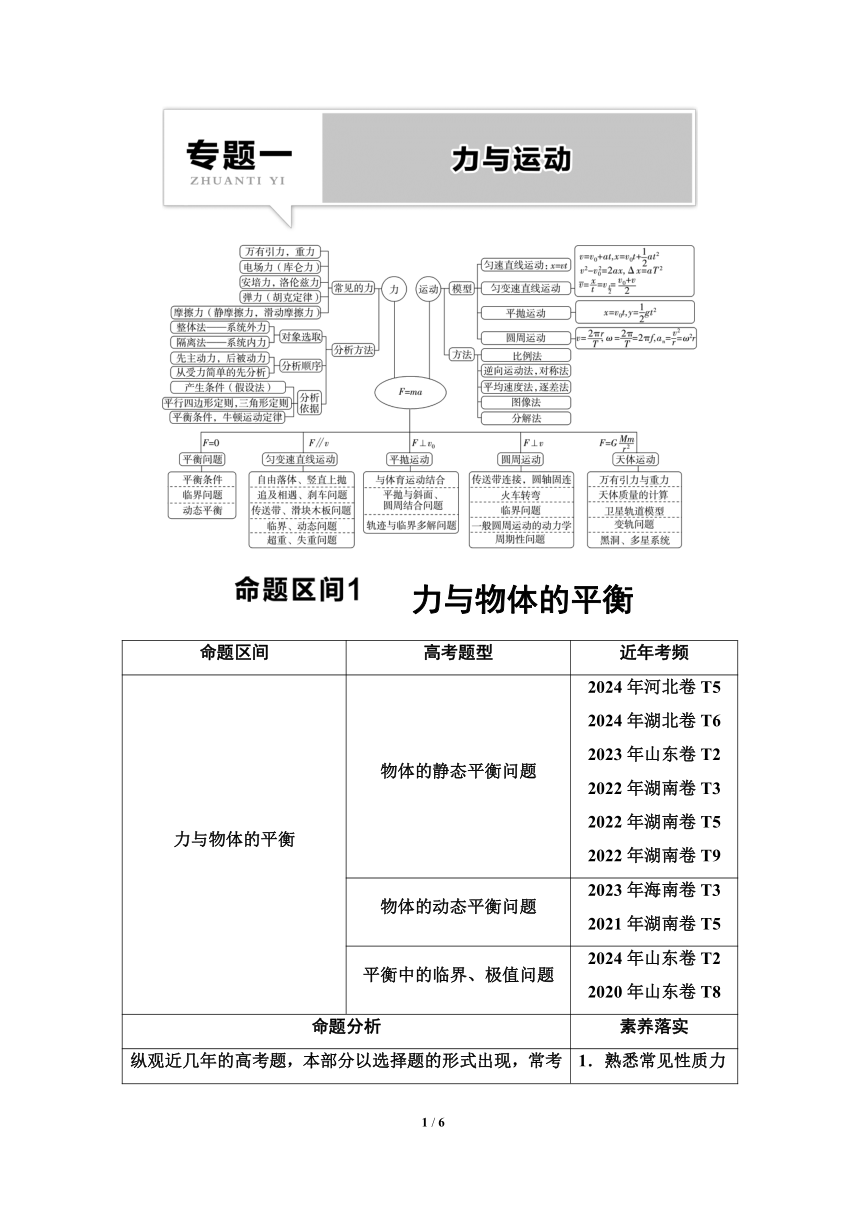 | |
| 格式 | docx | ||
| 文件大小 | 846.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-10-20 08:56:57 | ||
图片预览


文档简介
力与物体的平衡
命题区间 高考题型 近年考频
力与物体的平衡 物体的静态平衡问题 2024年河北卷T5 2024年湖北卷T6 2023年山东卷T2 2022年湖南卷T3 2022年湖南卷T5 2022年湖南卷T9
物体的动态平衡问题 2023年海南卷T3 2021年湖南卷T5
平衡中的临界、极值问题 2024年山东卷T2 2020年山东卷T8
命题分析 素养落实
纵观近几年的高考题,本部分以选择题的形式出现,常考查静态平衡和动态平衡问题,有时涉及电场中电荷的平衡问题和磁场中导体的平衡问题,考查的解题方法有合成法、正交分解法等。考题常以生产生活中的一些实际问题为背景,考查考生应用物理知识解决实际问题的能力。 1.熟悉常见性质力有无及方向的判断 2.灵活应用受力分析的一般步骤 3.掌握整体法、隔离法选取原则 4.平衡问题的解题方法
物体的静态平衡问题
求解共点力平衡问题的常用方法包括力的合成法、分解法及正交分解法,示意图如图所示。
合成法 分解法 正交分解法
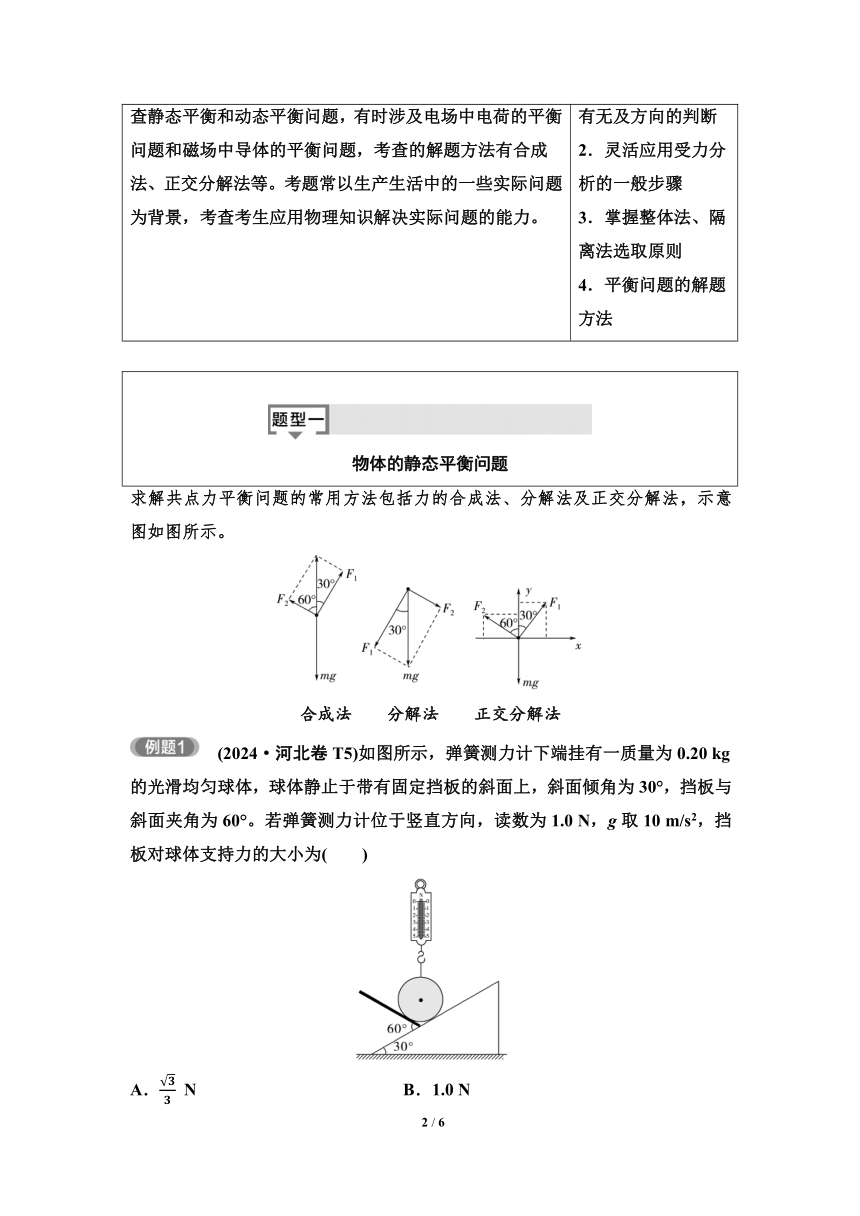
(2024·河北卷T5)如图所示,弹簧测力计下端挂有一质量为0.20 kg的光滑均匀球体,球体静止于带有固定挡板的斜面上,斜面倾角为30°,挡板与斜面夹角为60°。若弹簧测力计位于竖直方向,读数为1.0 N,g取10 m/s2,挡板对球体支持力的大小为( )
A. N B.1.0 N
C. N D.2.0 N
命题立意:本题考查力的静态平衡
第一步:正确受力分析
第二步:由几何关系确定力F、FN与竖直方向的夹角
第三步:由平衡条件利用正交分解或三角函数关系求出挡板对球体支持力
规范解答:
对小球受力分析如图所示
由几何关系易得力F与力FN与竖直方向的夹角均为30°,因此由正交分解方程可得
FNsin 30°=F sin 30°
FNcos 30°+F cos 30°+T=mg
解得F=FN= N
故选A。
[答案] A
难点:正确受力分析
易错:弹力方向判断错误或力三角形几何关系分析错误
物体的动态平衡问题
动态平衡问题的常用方法:(1)图解法;(2)解析法;(3)相似三角形法;(4)正弦定理法等。
(2021·湖南卷T5)质量为M的凹槽静止在水平地面上,内壁为半圆柱面,截面如图所示,A为半圆的最低点,B为半圆水平直径的端点。凹槽恰好与竖直墙面接触,内有一质量为m的小滑块。用推力F推动小滑块由A点向B点缓慢移动,力F的方向始终沿圆弧的切线方向,在此过程中所有摩擦均可忽略,下列说法正确的是( )
A.推力F先增大后减小
B.凹槽对滑块的支持力先减小后增大
C.墙面对凹槽的压力先增大后减小
D.水平地面对凹槽的支持力先减小后增大
命题立意:本题以小滑块在圆弧曲面的缓慢移动为背景,考查共点力的动态平衡问题
第一步:正确受力分析
第二步:用力的合成法作出FN1、F的合力
第三步:由平衡条件结合三角函数关系表示出FN1、F、FN′及FN2
规范解答:因小滑块由A点向B点缓慢移动过程中,所有摩擦均可忽略,对滑块受力分析,如图所示,由平衡条件有F=mg sin θ,FN1=mg cos θ,小滑块从A点缓慢移动到B点时,θ越来越大,则推力F越来越大,支持力FN1越来越小,所以A、B错误;对凹槽与滑块整体分析,墙面对凹槽的压力FN′=F cos θ=mg sin θcos θ=mg sin (2θ),由此可知随着θ变大,墙面对凹槽的压力先增大后减小,所以C正确;水平地面对凹槽的支持力为FN2=(M+m)g-F sin θ=(M+m)g-mg sin2θ,则θ越来越大时,水平地面对凹槽的支持力越来越小,所以D错误。
[答案] C
难点:正确受力分析,用三角函数表示各力
易错:在求解墙面对凹槽的压力和水平地面对凹槽的支持力时不知道使用整体法而造成错误
平衡中的临界、极值问题
解决临界极值问题的三种方法:解析法、图解法、极限法。解决此类问题重在形成清晰的物理图境,分析清楚物理过程,从而找出临界条件或达到极值的条件。要特别注意可能出现的多种情况。
(2020·山东卷T8)如图所示,一轻质光滑定滑轮固定在倾斜木板上,质量分别为m和2m的物块A、B,通过不可伸长的轻绳跨过滑轮连接,A、B间的接触面和轻绳均与木板平行。A与B间、B与木板间的动摩擦因数均为μ,设最大静摩擦力等于滑动摩擦力。当木板与水平面的夹角为45°时,物块A、B刚好要滑动,则μ的值为( )
A. B. C. D.
命题立意:本题属于应用性题目,以“滑轮斜面约束物体”为素材创设学习探索类情境,考查平衡中的临界、极值问题
第一步:正确受力分析
第二步:由平衡条件结合三角函数关系列出A、B物块沿斜面方向的平衡方程,求出μ
规范解答:当木板与水平面的夹角为45°时,两物块刚好滑动,对物块A受力分析如图①所示
① ②
沿斜面方向,A、B之间的滑动摩擦力f1=μN=μmg cos45°,根据平衡条件可知T=mg sin 45°+μmg cos 45°,对物块B受力分析如图②所示,沿斜面方向,B与斜面之间的滑动摩擦力f2=μN′=μ·3mg cos 45°,根据平衡条件可知2mg sin 45°=T′+μmg cos 45°+μ·3mg cos 45°,根据题意可知T=T′,联立可得2mg sin 45°=mg sin 45°+μmg cos 45°+μmg cos 45°+μ·3mg cos 45°,解得μ= ,A、B、D错误,C正确。
[答案] C
难点:正确对物块A、B受力分析,列出临界状态时的平衡方程
易错:(1)物块A对物块B摩擦力的方向误判为沿斜面向下
(2)倾斜木板对B摩擦力的大小误认为μ·2mg cos 45°
1 / 6
命题区间 高考题型 近年考频
力与物体的平衡 物体的静态平衡问题 2024年河北卷T5 2024年湖北卷T6 2023年山东卷T2 2022年湖南卷T3 2022年湖南卷T5 2022年湖南卷T9
物体的动态平衡问题 2023年海南卷T3 2021年湖南卷T5
平衡中的临界、极值问题 2024年山东卷T2 2020年山东卷T8
命题分析 素养落实
纵观近几年的高考题,本部分以选择题的形式出现,常考查静态平衡和动态平衡问题,有时涉及电场中电荷的平衡问题和磁场中导体的平衡问题,考查的解题方法有合成法、正交分解法等。考题常以生产生活中的一些实际问题为背景,考查考生应用物理知识解决实际问题的能力。 1.熟悉常见性质力有无及方向的判断 2.灵活应用受力分析的一般步骤 3.掌握整体法、隔离法选取原则 4.平衡问题的解题方法
物体的静态平衡问题
求解共点力平衡问题的常用方法包括力的合成法、分解法及正交分解法,示意图如图所示。
合成法 分解法 正交分解法
(2024·河北卷T5)如图所示,弹簧测力计下端挂有一质量为0.20 kg的光滑均匀球体,球体静止于带有固定挡板的斜面上,斜面倾角为30°,挡板与斜面夹角为60°。若弹簧测力计位于竖直方向,读数为1.0 N,g取10 m/s2,挡板对球体支持力的大小为( )
A. N B.1.0 N
C. N D.2.0 N
命题立意:本题考查力的静态平衡
第一步:正确受力分析
第二步:由几何关系确定力F、FN与竖直方向的夹角
第三步:由平衡条件利用正交分解或三角函数关系求出挡板对球体支持力
规范解答:
对小球受力分析如图所示
由几何关系易得力F与力FN与竖直方向的夹角均为30°,因此由正交分解方程可得
FNsin 30°=F sin 30°
FNcos 30°+F cos 30°+T=mg
解得F=FN= N
故选A。
[答案] A
难点:正确受力分析
易错:弹力方向判断错误或力三角形几何关系分析错误
物体的动态平衡问题
动态平衡问题的常用方法:(1)图解法;(2)解析法;(3)相似三角形法;(4)正弦定理法等。
(2021·湖南卷T5)质量为M的凹槽静止在水平地面上,内壁为半圆柱面,截面如图所示,A为半圆的最低点,B为半圆水平直径的端点。凹槽恰好与竖直墙面接触,内有一质量为m的小滑块。用推力F推动小滑块由A点向B点缓慢移动,力F的方向始终沿圆弧的切线方向,在此过程中所有摩擦均可忽略,下列说法正确的是( )
A.推力F先增大后减小
B.凹槽对滑块的支持力先减小后增大
C.墙面对凹槽的压力先增大后减小
D.水平地面对凹槽的支持力先减小后增大
命题立意:本题以小滑块在圆弧曲面的缓慢移动为背景,考查共点力的动态平衡问题
第一步:正确受力分析
第二步:用力的合成法作出FN1、F的合力
第三步:由平衡条件结合三角函数关系表示出FN1、F、FN′及FN2
规范解答:因小滑块由A点向B点缓慢移动过程中,所有摩擦均可忽略,对滑块受力分析,如图所示,由平衡条件有F=mg sin θ,FN1=mg cos θ,小滑块从A点缓慢移动到B点时,θ越来越大,则推力F越来越大,支持力FN1越来越小,所以A、B错误;对凹槽与滑块整体分析,墙面对凹槽的压力FN′=F cos θ=mg sin θcos θ=mg sin (2θ),由此可知随着θ变大,墙面对凹槽的压力先增大后减小,所以C正确;水平地面对凹槽的支持力为FN2=(M+m)g-F sin θ=(M+m)g-mg sin2θ,则θ越来越大时,水平地面对凹槽的支持力越来越小,所以D错误。
[答案] C
难点:正确受力分析,用三角函数表示各力
易错:在求解墙面对凹槽的压力和水平地面对凹槽的支持力时不知道使用整体法而造成错误
平衡中的临界、极值问题
解决临界极值问题的三种方法:解析法、图解法、极限法。解决此类问题重在形成清晰的物理图境,分析清楚物理过程,从而找出临界条件或达到极值的条件。要特别注意可能出现的多种情况。
(2020·山东卷T8)如图所示,一轻质光滑定滑轮固定在倾斜木板上,质量分别为m和2m的物块A、B,通过不可伸长的轻绳跨过滑轮连接,A、B间的接触面和轻绳均与木板平行。A与B间、B与木板间的动摩擦因数均为μ,设最大静摩擦力等于滑动摩擦力。当木板与水平面的夹角为45°时,物块A、B刚好要滑动,则μ的值为( )
A. B. C. D.
命题立意:本题属于应用性题目,以“滑轮斜面约束物体”为素材创设学习探索类情境,考查平衡中的临界、极值问题
第一步:正确受力分析
第二步:由平衡条件结合三角函数关系列出A、B物块沿斜面方向的平衡方程,求出μ
规范解答:当木板与水平面的夹角为45°时,两物块刚好滑动,对物块A受力分析如图①所示
① ②
沿斜面方向,A、B之间的滑动摩擦力f1=μN=μmg cos45°,根据平衡条件可知T=mg sin 45°+μmg cos 45°,对物块B受力分析如图②所示,沿斜面方向,B与斜面之间的滑动摩擦力f2=μN′=μ·3mg cos 45°,根据平衡条件可知2mg sin 45°=T′+μmg cos 45°+μ·3mg cos 45°,根据题意可知T=T′,联立可得2mg sin 45°=mg sin 45°+μmg cos 45°+μmg cos 45°+μ·3mg cos 45°,解得μ= ,A、B、D错误,C正确。
[答案] C
难点:正确对物块A、B受力分析,列出临界状态时的平衡方程
易错:(1)物块A对物块B摩擦力的方向误判为沿斜面向下
(2)倾斜木板对B摩擦力的大小误认为μ·2mg cos 45°
1 / 6
同课章节目录
