2.2圆的对称性暑假预习练(含解析) 苏科版数学九年级上册
文档属性
| 名称 | 2.2圆的对称性暑假预习练(含解析) 苏科版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-09 11:32:28 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2.2圆的对称性
学校:___________姓名:___________班级:___________考号:___________
一、单选题
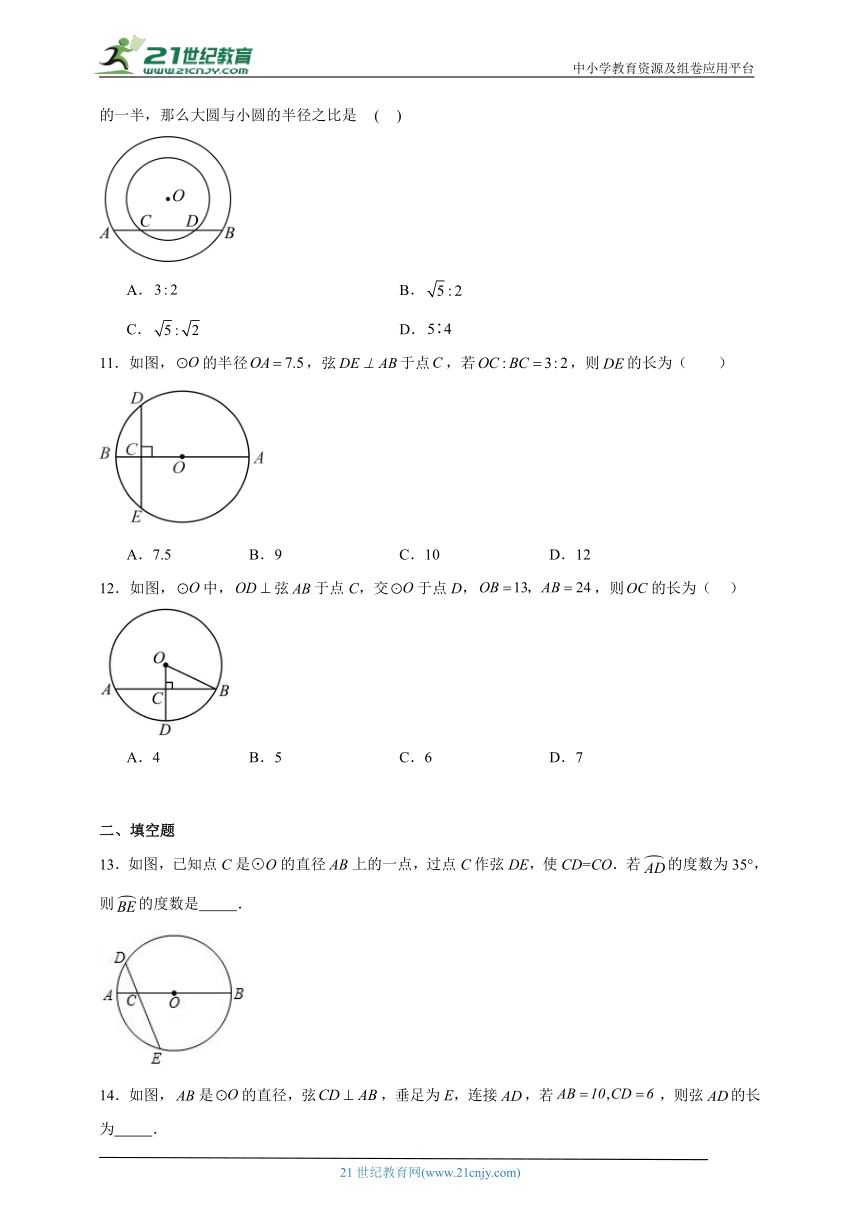
1.如图,已知半径OD与弦AB互相垂直,垂足为点C,若AB=8cm,CD=3cm,则圆O的半径为( )
A.cm B.5cm C.4cm D.cm
2.如图,点A、B、C、D在⊙O上,BC=DC,若∠BOD=124°,则∠A的大小为( )
A.27° B.31° C.56° D.63°
3.如图所示,在⊙O中,=,∠A=30°,则∠B=( )
A.150° B.75° C.60° D.15°
4.如图,⊙O的直径,是⊙O的弦,,垂足为,,则的长为( )
A. B. C.16 D.8
5.如图,在⊙O中,直径AB与弦MN相交于点P,∠NPB=45°,若AP=2,BP=6,则MN的长为( )
A. B.2 C.2 D.8
6.如图,将半径为的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )
A.4cm B.2cm C.cm D.cm
7.如图,点D是直径为10的中一点,若长为3,则过点D的所有弦中,最长弦与最短弦的长度差为( )
A.2 B.6 C.14 D.18
8.如图,在半径为5的⊙O中,如果弦AB的长为8,那么它的弦心距OC等于( )
A.2 B.3 C.4 D.6
9.⊙O的直径是10,两平行弦的长度分别是6和8,那么这两弦的距离是( )
A.1 B.7 C.8 D.1或7
10.如图所示,在同心圆中,大圆的弦交小圆于C,D,已知,的弦心距等于长的一半,那么大圆与小圆的半径之比是 ( )
A. B.
C. D.
11.如图,的半径,弦于点,若,则的长为( )
A.7.5 B.9 C.10 D.12
12.如图,中,弦于点C,交于点D,,则的长为( )
A.4 B.5 C.6 D.7
二、填空题
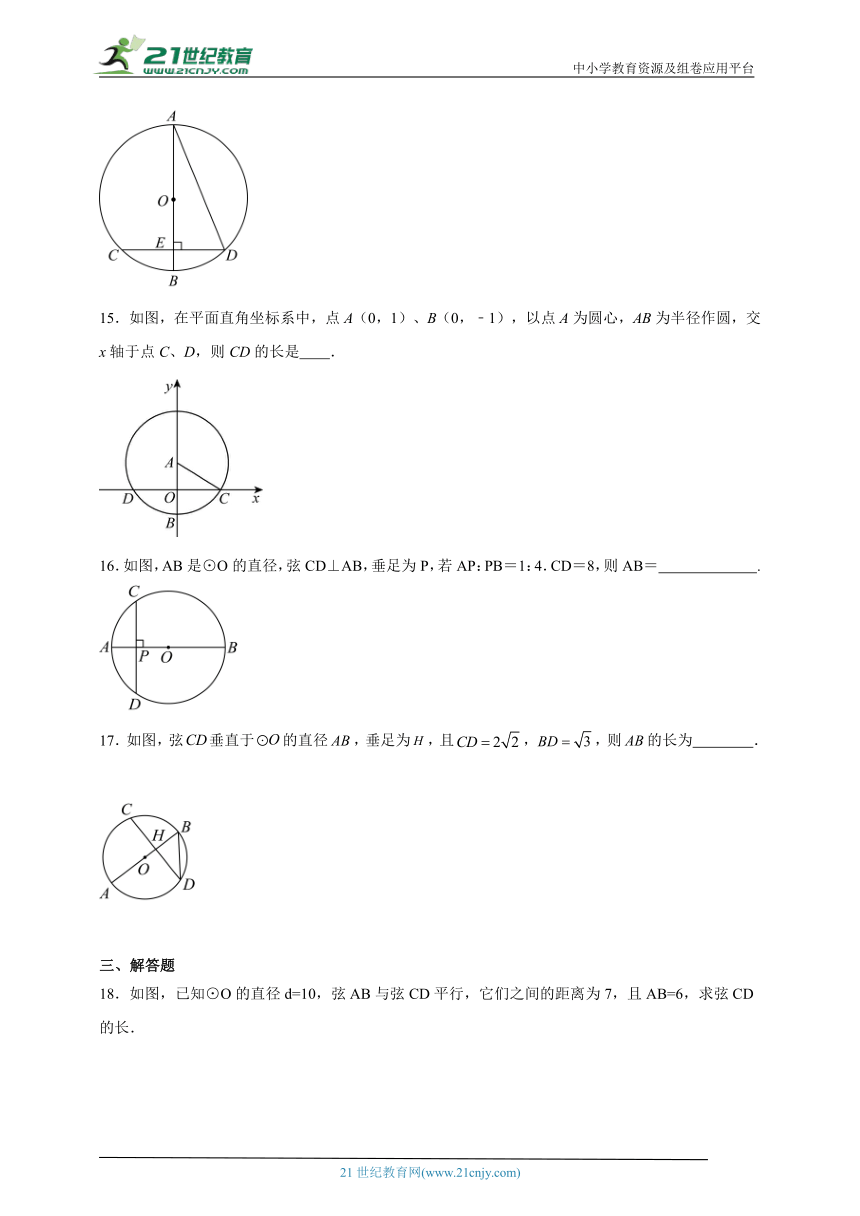
13.如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为35°,则的度数是 .
14.如图,是的直径,弦,垂足为E,连接,若,则弦的长为 .
15.如图,在平面直角坐标系中,点A(0,1)、B(0,﹣1),以点A为圆心,AB为半径作圆,交x轴于点C、D,则CD的长是 .
16.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若AP:PB=1:4.CD=8,则AB= .
17.如图,弦垂直于的直径,垂足为,且,,则的长为 .
三、解答题
18.如图,已知⊙O的直径d=10,弦AB与弦CD平行,它们之间的距离为7,且AB=6,求弦CD的长.
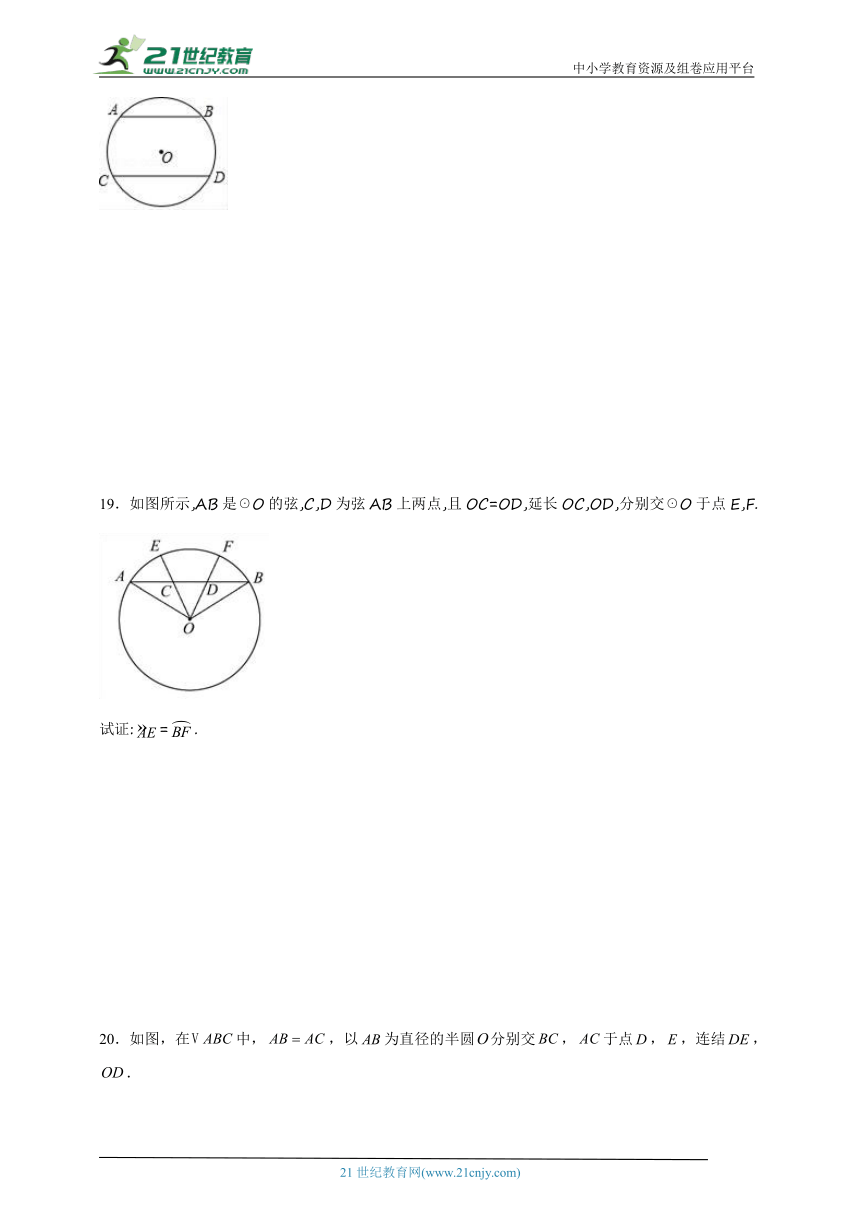
19.如图所示,AB是☉O的弦,C,D为弦AB上两点,且OC=OD,延长OC,OD,分别交☉O于点E,F.
试证:=.
20.如图,在中,,以为直径的半圆分别交,于点,,连结,.
(1)求证:.
(2)当,的度数之比为时,求四边形四个内角的度数.
21.某公路上有一隧道,顶部是圆弧形拱顶,圆心为,隧道的水平宽为,离地面的高度,拱顶最高处离地面的高度为,在拱顶的,处安装照明灯,且,离地面的高度相等都等于,求的长.
22.已知:如图,AB是⊙O的直径,弦CD⊥AB于E,∠ACD=30°,AE=2cm.求DB长.
23.如图,点C是上的点,CD⊥OA于D,CE⊥OB于E,若CD=CE.
求证:点C是的中点.
24.如图,在⊙O中,CD为直径,AB为弦,且CD平分AB于E,OE=3cm,AB=8cm,求⊙O的半径.
《2.2圆的对称性》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A B B A C A A B D C
题号 11 12
答案 D B
1.A
【分析】连接AO,根据垂径定理可知AC=AB=4cm,设半径为x,则OC=x-3,根据勾股定理即可求得x的值.
【详解】解:如图,连接AO,
∵半径OD与弦AB互相垂直,AB=8cm,
∴AC=AB=4cm.
设半径为x,则OC=x﹣3,
在Rt△ACO中,AO2=AC2+OC2,
即x2=42+(x﹣3)2,
解得:x=.
∴半径为cm.
故选A.
【点睛】本题考查了垂径定理及勾股定理的知识,解答本题的关键是熟练掌握垂径定理、勾股定理的内容.
2.B
【分析】根据圆心角、弧、弦之间的关系得出∠DOC=∠BOC,求出∠BOC的度数,根据圆周角定理得出∠A=∠BOC,再求出答案即可.
【详解】解:连接OC,
∵BC=DC,
∴∠DOC=∠BOC,
∵∠BOD=124°,
∴∠BOC=∠BOD=62°,
∴∠A=∠BOC=31°(圆周角定理),
故选:B.
【点睛】本考查了圆周角定理和圆心角、弧、弦之间的关系,能熟记知识点是解此题的关键,注意:一条弧所对的圆周角等于它所对的圆心角的一半.
3.B
【详解】∵在⊙O中,=,
∴AB=AC,
∴△ABC是等腰三角形,
∴∠B=∠C;又∠A=30°,
∴∠B==75°(三角形内角和定理).
故选B.
考点:圆心角、弧、弦的关系.
4.A
【分析】连接OA,先根据⊙O的直径CD=12,CP:PO=1:2求出CO及OP的长,再根据勾股定理可求出AP的长,进而得出结论.
【详解】连接OA,
∵⊙O的直径CD=12,CP:PO=1:2,
∴CO=6,PO=4,
∵AB⊥CD,
∴AP= == ,
∴AB=2AP=.
故选:A.
【点睛】本题考查了垂径定理和勾股定理的应用,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式成立,知道这三个量中的任意两个,就可以求出另外一个.
5.C
【分析】过点O作OD⊥MN于点D,连接ON,先根据AB是直径,AP=2,BP=6求出⊙O的半径,故可得出OP的长,因为∠NPB=45°,所以△OPD是等腰直角三角形,再根据勾股定理求出OD的长,故可得出DN的长,由此即可得出结论.
【详解】解:过点O作OD⊥MN于点D,连接ON,则MN=2DN,
∵AB是⊙O的直径,AP=2,BP=6,
∴⊙O的半径=×(2+6)=4,
∴OP=4﹣AP=4﹣2=2,
∵∠NPB=45°,
∴△OPD是等腰直角三角形,
∴OD=,
在Rt△ODN中,
DN=,
∴MN=2DN=2.
故答案为:C.
【点睛】本题考查的是垂径定理,勾股定理以及等腰三角形的判定与性质等知识,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
6.A
【分析】连接AO,过O作OD⊥AB,交于点D,交弦AB与点E,根据折叠的性质及垂径定理得到AE=BE,再根据勾股定理即可求解.
【详解】如图所示,连接AO,过O作OD⊥AB,交于点D,交弦AB与点E,
∵折叠后恰好经过圆心,
∴OE=DE,
∵半径为4,
∴OE=2,
∵OD⊥AB,
∴AE=AB,
在Rt△AOE中,AE==2
∴AB=2AE=4
故选A.
【点睛】此题主要考查垂径定理,解题的关键是熟知垂径定理的应用.
7.A
【分析】要满足最短弦,只需满足垂直于该弦,再用垂径定理和勾股定理求得最短弦,由过点D的所有弦中,最长弦是直径,即可得到答案.
【详解】解:根据题意可知,要满足最短弦,只需满足垂直于该弦,设该最短弦是,如图,于点D,
∴,,
∴,
∴,
∵过点D的所有弦中,最长弦是直径,
∴最长弦与最短弦的长度差为,
故选:A
【点睛】此题考查了垂径定理、勾股定理等知识,熟练掌握过圆内一点的最长弦和最短弦是解题的关键.
8.B
【详解】解:如图,连接OA,在Rt△OAC中,OA=5,AC=4,
在Rt△OAC中,OA=5,AC=4,则,
故选:B
9.D
【分析】此题要分情况讨论:①两条线段在圆心的同侧,②两条线段在圆心的异侧,然后结合图分别求出两条线段之间的距离即可.
【详解】解:①两条线段在圆心的同侧,如图,AB=8,CD=6,且ABCD,
先过O作OF⊥CD,垂足是F,交AB于E,连接OA,OC,
∵ABCD,OF⊥CD,
∴OF⊥AB,
∴∠OEA=90°,AE=AB=4,
在Rt△AOE中,AE=4,OA==5,
∴OE==3,
同理可求OF=4,
∴EF=OF OE=1;
②两条线段在圆心的异侧,如图,AB=8,CD=6,且ABCD,
先过O作OF⊥CD,垂足是F,反向延长交AB于E,连接OA,OC,
∵ABCD,OF⊥CD,
∴OF⊥AB,
∴∠OEA=90°,AE=AB=4,
在Rt△AOE中,AE=4,OA=5,
∴OE==3,
同理可求OF=4,
∴EF=OE+OF=7.
故选D.
【点睛】本题考查了垂径定理、勾股定理,解题的关键是作辅助线,构造直角三角形,注意分情况讨论.
10.C
【分析】本题主要考查了垂径定理,勾股定理,过O作于E,连接,,设,
由垂径定理求出,,在根据已知条件得出,在利用勾股定理求出和,然后相比即可得出答案.
【详解】解:过O作于E,连接,,
设,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∵等于的一半,
∴,
在中,,
在中,,
∴.
故选∶C.
11.D
【分析】连接OD,由题意得OD=OB=OA=7.5,OC=3/5OB=4.5,再由垂径定理得CD=CE=1/2DE,然后由勾股定理求出CD=6,即可得出答案.
【详解】解:连接OD,如图所示:
∵⊙O的半径OA=7.5,OC:BC=3:2,
∴OD=OB=OA=7.5,OCOB=4.5,
∵DE⊥AB,
∴CD=CEDE,
∴CD6,
∴DE=2CD=12,
故选:D.
【点睛】本题考查了垂径定理和勾股定理;熟练掌握垂径定理和勾股定理是解题的关键.
12.B
【分析】根据垂径定理求出的长,再根据勾股定理求出的长即可.
【详解】解:∵,,
∴,
在中,.
故选:B.
【点睛】本题考查了垂径定理,勾股定理,熟练掌握垂径定理是解题的关键.
13.105°.
【分析】连接OD、OE,根据圆心角、弧、弦的关系定理求出∠AOD=35°,根据等腰三角形的性质和三角形内角和定理计算即可.
【详解】解:连接OD、OE,
∵的度数为35°,
∴∠AOD=35°,
∵CD=CO,
∴∠ODC=∠AOD=35°,
∵OD=OE,
∴∠ODC=∠E=35°,
∴∠DOE=180°-∠ODC-∠E=180°-35°-35°=110°,
∴∠AOE=∠DOE-∠AOD=110°-35°=75°,
∴∠BOE=180°-∠AOE=180°-75°=105°,
∴的度数是105°.
故答案为105°.
【点睛】本题考查了圆心角、弧、弦的关系定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
14.
【分析】本题主要考查垂径定理,熟练掌握垂径定理是解题的关键.由题意易得,根据勾股定理可求的长,然后问题可求解.
【详解】解:连接,
∵是的直径,,
∴,
∵,
∴,
∴,
∴,
∴,
故答案为:.
15.
【分析】根据题意在中求出,利用垂径定理得出结果.
【详解】由题意,在中,,,
由垂径定理知,,
故答案为:.
【点睛】本题考查了勾股定理及垂径定理,熟练掌握垂径定理是解决本题的关键.
16.10
【分析】AB是直径,AB⊥CD所以利用垂径定理得到CP=PD,再利用相交弦定理就可以得到CP2=AP BP,然后求出直径的长.
【详解】∵AB为直径,CD⊥AB,
∵CD=8,
∴PC=PD=4m设AP=x,则PB=4x
由相交弦定理,得x×4x=4×4,
∴x=2,
∴AB的长为10.
故答案为10
【点睛】此题比较简单,主要考查垂径定理和相交弦定理的应用.
17.
【分析】根据垂径定理和相交弦定理求解.
【详解】连接OD,如图所示:
由垂径定理得HD=,由勾股定理得HB=1,
设圆O的半径为R,在Rt△ODH中,OH=R-1,DH=
则R2=()2+(R-1)2,由此得2R=3,
或由相交弦定理得()2=1×( 2R-1),由此得2R=3,所以AB=3.
故答案是:3.
【点睛】考查了垂径定理、勾股定理或相交弦定理.
18.8
【分析】作OM⊥AB于M,ON⊥CD于N,连接OA、OC,根据垂径定理得到
根据AB∥CD,得到点M、O、N在同一条直线上,在Rt△AOM中,根据勾股定理求出
进而求出ON,在Rt△CON中,根据勾股定理求出根据垂径定理即可求出弦CD的长.
【详解】作OM⊥AB于M,ON⊥CD于N,连接OA、OC,
则
∵AB∥CD,
∴点M、O、N在同一条直线上,
在Rt△AOM中,
∴ON=MN﹣OM=3,
在Rt△CON中,
∵ON⊥CD,
∴CD=2CN=8.
【点睛】考查勾股定理以及垂径定理,作出辅助线,构造直角三角形是解题的关键.
19.证明见解析
【详解】试题分析:根据等腰三角形的性质由OC=OD得∠OCD=∠ODC,由OA=OB得∠A=∠B,再根据三角形外角性质得∠OCD=∠A+∠AOC,∠ODC=∠B+∠BOD,利用等量代换得到∠AOC=∠BOD,然后根据在同圆和等圆中,相等的圆心角所对的弧相等即可得到结论.
证明:∵OC=OD,∴∠OCD=∠ODC.
∵AO=OB,∴∠A=∠B.
∴∠OCD-∠A=∠ODC-∠B,
即∠AOC=∠BOD,
即∠AOE=∠BOF.∴=.
点睛:本题考查了圆心角、弧、弦的关系:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
20.(1)证明见解析;(2),,,.
【分析】(1)连接AD后,证明这两条弧所对的圆周角相等,即,该题得证;
(2)由这两条弧度数之比为4:5,分别求出它们的度数,再根据 ,求出和的度数,即可求出 和,利用圆的内接四边形对角互补可以得到另外两个内角的度数.
【详解】解:(1)如图,连结,
∵是直径,
∴,
∵,
∴,
∴.
(2)∵,与的度数之比为,
∴,,
∵,∴,
∴,
∴,,
∵,,
∴,,
∴,,,.
【点睛】本题考查了圆中的弧和圆周角之间的关系,学生应在理解圆周角定理以及其推论的同时,能熟练应用它们,解决本题的关键是通过连线,构造两弧所对的圆周角,通过角的关系来证明弧的关系,同时应明白圆周角等于其所对弧的度数的二分之一,能由弧度求出角度,只有牢牢记住它们的关系,才能灵活地在角与弧之间进行转化,求出答案.
21.
【分析】根据题意和垂径定理得到,根据勾股定理求得半径,进而利用勾股定理求得,即可求得.
【详解】设于交于G,与交于H,
∵,
∴,
设圆拱的半径为r,
在中,,
∴,
解得,
∴,
∴,
在中,,
∴,
解得,
∴,
∴.
【点睛】本题考查了垂径定理的应用,作出辅助线构建直角三角形,利用勾股定理求解是解题的关键.
22.DB=cm
【分析】由AB是⊙O的直径,弦CD⊥AB,根据垂径定理,可得CE=DE,∠AEC=∠DEB=90°,然后由含30°角的直角三角形的性质,即可求得EC与DE的长,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可求得∠B=30°,继而求得DB的长.
【详解】∵AB是⊙O的直径,弦CD⊥AB,
∴CE=DE,∠AEC=∠DEB=90°,
∵∠B=∠ACD=30°,
在Rt△ACE中,AC=2AE=4cm,
∴CE==2(cm),
∴DE=2cm,
在Rt△BDE中,∠B=30°,
∴BD=2DE=4cm.
∴DB的长为4cm.
【点睛】本题考查了垂径定理,在同圆或等圆中同弧或等弧所对的圆周角相等,含30°角直角三角形的性质及勾股定理,其中含30°角直角三角形的性质是解题的关键.
23.见解析
【分析】连接OC,利用HL可证明△ODB≌△EDC,可得∠DOC=∠EOC,根据在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等即可证明,可得点C是的中点.
【详解】连接OC,
∵CD=CE,OC=OC,CD⊥OA,CE⊥OB,
∴△ODB≌△EDC(HL),
∴∠DOC=∠EOC,
∵∠DOC与∠EOC分别是和所对的圆心角,
∴,
∴点C是的中点.
【点睛】此题主要考查了全等三角形的判定与性质及圆心角、弧、弦的关系,在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
24.5cm
【分析】首先连接OA,根据垂径定理可得CD⊥AB,AE=4,根据勾股定理求出OA的长度.
【详解】连接OA,CD为直径,且CD平分AB于E,
∴CD⊥AB,AE=AB=4cm,
在Rt△OAE中,
∴⊙O的半径为5cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.2圆的对称性
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,已知半径OD与弦AB互相垂直,垂足为点C,若AB=8cm,CD=3cm,则圆O的半径为( )
A.cm B.5cm C.4cm D.cm
2.如图,点A、B、C、D在⊙O上,BC=DC,若∠BOD=124°,则∠A的大小为( )
A.27° B.31° C.56° D.63°
3.如图所示,在⊙O中,=,∠A=30°,则∠B=( )
A.150° B.75° C.60° D.15°
4.如图,⊙O的直径,是⊙O的弦,,垂足为,,则的长为( )
A. B. C.16 D.8
5.如图,在⊙O中,直径AB与弦MN相交于点P,∠NPB=45°,若AP=2,BP=6,则MN的长为( )
A. B.2 C.2 D.8
6.如图,将半径为的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )
A.4cm B.2cm C.cm D.cm
7.如图,点D是直径为10的中一点,若长为3,则过点D的所有弦中,最长弦与最短弦的长度差为( )
A.2 B.6 C.14 D.18
8.如图,在半径为5的⊙O中,如果弦AB的长为8,那么它的弦心距OC等于( )
A.2 B.3 C.4 D.6
9.⊙O的直径是10,两平行弦的长度分别是6和8,那么这两弦的距离是( )
A.1 B.7 C.8 D.1或7
10.如图所示,在同心圆中,大圆的弦交小圆于C,D,已知,的弦心距等于长的一半,那么大圆与小圆的半径之比是 ( )
A. B.
C. D.
11.如图,的半径,弦于点,若,则的长为( )
A.7.5 B.9 C.10 D.12
12.如图,中,弦于点C,交于点D,,则的长为( )
A.4 B.5 C.6 D.7
二、填空题
13.如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为35°,则的度数是 .
14.如图,是的直径,弦,垂足为E,连接,若,则弦的长为 .
15.如图,在平面直角坐标系中,点A(0,1)、B(0,﹣1),以点A为圆心,AB为半径作圆,交x轴于点C、D,则CD的长是 .
16.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若AP:PB=1:4.CD=8,则AB= .
17.如图,弦垂直于的直径,垂足为,且,,则的长为 .
三、解答题
18.如图,已知⊙O的直径d=10,弦AB与弦CD平行,它们之间的距离为7,且AB=6,求弦CD的长.
19.如图所示,AB是☉O的弦,C,D为弦AB上两点,且OC=OD,延长OC,OD,分别交☉O于点E,F.
试证:=.
20.如图,在中,,以为直径的半圆分别交,于点,,连结,.
(1)求证:.
(2)当,的度数之比为时,求四边形四个内角的度数.
21.某公路上有一隧道,顶部是圆弧形拱顶,圆心为,隧道的水平宽为,离地面的高度,拱顶最高处离地面的高度为,在拱顶的,处安装照明灯,且,离地面的高度相等都等于,求的长.
22.已知:如图,AB是⊙O的直径,弦CD⊥AB于E,∠ACD=30°,AE=2cm.求DB长.
23.如图,点C是上的点,CD⊥OA于D,CE⊥OB于E,若CD=CE.
求证:点C是的中点.
24.如图,在⊙O中,CD为直径,AB为弦,且CD平分AB于E,OE=3cm,AB=8cm,求⊙O的半径.
《2.2圆的对称性》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A B B A C A A B D C
题号 11 12
答案 D B
1.A
【分析】连接AO,根据垂径定理可知AC=AB=4cm,设半径为x,则OC=x-3,根据勾股定理即可求得x的值.
【详解】解:如图,连接AO,
∵半径OD与弦AB互相垂直,AB=8cm,
∴AC=AB=4cm.
设半径为x,则OC=x﹣3,
在Rt△ACO中,AO2=AC2+OC2,
即x2=42+(x﹣3)2,
解得:x=.
∴半径为cm.
故选A.
【点睛】本题考查了垂径定理及勾股定理的知识,解答本题的关键是熟练掌握垂径定理、勾股定理的内容.
2.B
【分析】根据圆心角、弧、弦之间的关系得出∠DOC=∠BOC,求出∠BOC的度数,根据圆周角定理得出∠A=∠BOC,再求出答案即可.
【详解】解:连接OC,
∵BC=DC,
∴∠DOC=∠BOC,
∵∠BOD=124°,
∴∠BOC=∠BOD=62°,
∴∠A=∠BOC=31°(圆周角定理),
故选:B.
【点睛】本考查了圆周角定理和圆心角、弧、弦之间的关系,能熟记知识点是解此题的关键,注意:一条弧所对的圆周角等于它所对的圆心角的一半.
3.B
【详解】∵在⊙O中,=,
∴AB=AC,
∴△ABC是等腰三角形,
∴∠B=∠C;又∠A=30°,
∴∠B==75°(三角形内角和定理).
故选B.
考点:圆心角、弧、弦的关系.
4.A
【分析】连接OA,先根据⊙O的直径CD=12,CP:PO=1:2求出CO及OP的长,再根据勾股定理可求出AP的长,进而得出结论.
【详解】连接OA,
∵⊙O的直径CD=12,CP:PO=1:2,
∴CO=6,PO=4,
∵AB⊥CD,
∴AP= == ,
∴AB=2AP=.
故选:A.
【点睛】本题考查了垂径定理和勾股定理的应用,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式成立,知道这三个量中的任意两个,就可以求出另外一个.
5.C
【分析】过点O作OD⊥MN于点D,连接ON,先根据AB是直径,AP=2,BP=6求出⊙O的半径,故可得出OP的长,因为∠NPB=45°,所以△OPD是等腰直角三角形,再根据勾股定理求出OD的长,故可得出DN的长,由此即可得出结论.
【详解】解:过点O作OD⊥MN于点D,连接ON,则MN=2DN,
∵AB是⊙O的直径,AP=2,BP=6,
∴⊙O的半径=×(2+6)=4,
∴OP=4﹣AP=4﹣2=2,
∵∠NPB=45°,
∴△OPD是等腰直角三角形,
∴OD=,
在Rt△ODN中,
DN=,
∴MN=2DN=2.
故答案为:C.
【点睛】本题考查的是垂径定理,勾股定理以及等腰三角形的判定与性质等知识,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
6.A
【分析】连接AO,过O作OD⊥AB,交于点D,交弦AB与点E,根据折叠的性质及垂径定理得到AE=BE,再根据勾股定理即可求解.
【详解】如图所示,连接AO,过O作OD⊥AB,交于点D,交弦AB与点E,
∵折叠后恰好经过圆心,
∴OE=DE,
∵半径为4,
∴OE=2,
∵OD⊥AB,
∴AE=AB,
在Rt△AOE中,AE==2
∴AB=2AE=4
故选A.
【点睛】此题主要考查垂径定理,解题的关键是熟知垂径定理的应用.
7.A
【分析】要满足最短弦,只需满足垂直于该弦,再用垂径定理和勾股定理求得最短弦,由过点D的所有弦中,最长弦是直径,即可得到答案.
【详解】解:根据题意可知,要满足最短弦,只需满足垂直于该弦,设该最短弦是,如图,于点D,
∴,,
∴,
∴,
∵过点D的所有弦中,最长弦是直径,
∴最长弦与最短弦的长度差为,
故选:A
【点睛】此题考查了垂径定理、勾股定理等知识,熟练掌握过圆内一点的最长弦和最短弦是解题的关键.
8.B
【详解】解:如图,连接OA,在Rt△OAC中,OA=5,AC=4,
在Rt△OAC中,OA=5,AC=4,则,
故选:B
9.D
【分析】此题要分情况讨论:①两条线段在圆心的同侧,②两条线段在圆心的异侧,然后结合图分别求出两条线段之间的距离即可.
【详解】解:①两条线段在圆心的同侧,如图,AB=8,CD=6,且ABCD,
先过O作OF⊥CD,垂足是F,交AB于E,连接OA,OC,
∵ABCD,OF⊥CD,
∴OF⊥AB,
∴∠OEA=90°,AE=AB=4,
在Rt△AOE中,AE=4,OA==5,
∴OE==3,
同理可求OF=4,
∴EF=OF OE=1;
②两条线段在圆心的异侧,如图,AB=8,CD=6,且ABCD,
先过O作OF⊥CD,垂足是F,反向延长交AB于E,连接OA,OC,
∵ABCD,OF⊥CD,
∴OF⊥AB,
∴∠OEA=90°,AE=AB=4,
在Rt△AOE中,AE=4,OA=5,
∴OE==3,
同理可求OF=4,
∴EF=OE+OF=7.
故选D.
【点睛】本题考查了垂径定理、勾股定理,解题的关键是作辅助线,构造直角三角形,注意分情况讨论.
10.C
【分析】本题主要考查了垂径定理,勾股定理,过O作于E,连接,,设,
由垂径定理求出,,在根据已知条件得出,在利用勾股定理求出和,然后相比即可得出答案.
【详解】解:过O作于E,连接,,
设,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∵等于的一半,
∴,
在中,,
在中,,
∴.
故选∶C.
11.D
【分析】连接OD,由题意得OD=OB=OA=7.5,OC=3/5OB=4.5,再由垂径定理得CD=CE=1/2DE,然后由勾股定理求出CD=6,即可得出答案.
【详解】解:连接OD,如图所示:
∵⊙O的半径OA=7.5,OC:BC=3:2,
∴OD=OB=OA=7.5,OCOB=4.5,
∵DE⊥AB,
∴CD=CEDE,
∴CD6,
∴DE=2CD=12,
故选:D.
【点睛】本题考查了垂径定理和勾股定理;熟练掌握垂径定理和勾股定理是解题的关键.
12.B
【分析】根据垂径定理求出的长,再根据勾股定理求出的长即可.
【详解】解:∵,,
∴,
在中,.
故选:B.
【点睛】本题考查了垂径定理,勾股定理,熟练掌握垂径定理是解题的关键.
13.105°.
【分析】连接OD、OE,根据圆心角、弧、弦的关系定理求出∠AOD=35°,根据等腰三角形的性质和三角形内角和定理计算即可.
【详解】解:连接OD、OE,
∵的度数为35°,
∴∠AOD=35°,
∵CD=CO,
∴∠ODC=∠AOD=35°,
∵OD=OE,
∴∠ODC=∠E=35°,
∴∠DOE=180°-∠ODC-∠E=180°-35°-35°=110°,
∴∠AOE=∠DOE-∠AOD=110°-35°=75°,
∴∠BOE=180°-∠AOE=180°-75°=105°,
∴的度数是105°.
故答案为105°.
【点睛】本题考查了圆心角、弧、弦的关系定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
14.
【分析】本题主要考查垂径定理,熟练掌握垂径定理是解题的关键.由题意易得,根据勾股定理可求的长,然后问题可求解.
【详解】解:连接,
∵是的直径,,
∴,
∵,
∴,
∴,
∴,
∴,
故答案为:.
15.
【分析】根据题意在中求出,利用垂径定理得出结果.
【详解】由题意,在中,,,
由垂径定理知,,
故答案为:.
【点睛】本题考查了勾股定理及垂径定理,熟练掌握垂径定理是解决本题的关键.
16.10
【分析】AB是直径,AB⊥CD所以利用垂径定理得到CP=PD,再利用相交弦定理就可以得到CP2=AP BP,然后求出直径的长.
【详解】∵AB为直径,CD⊥AB,
∵CD=8,
∴PC=PD=4m设AP=x,则PB=4x
由相交弦定理,得x×4x=4×4,
∴x=2,
∴AB的长为10.
故答案为10
【点睛】此题比较简单,主要考查垂径定理和相交弦定理的应用.
17.
【分析】根据垂径定理和相交弦定理求解.
【详解】连接OD,如图所示:
由垂径定理得HD=,由勾股定理得HB=1,
设圆O的半径为R,在Rt△ODH中,OH=R-1,DH=
则R2=()2+(R-1)2,由此得2R=3,
或由相交弦定理得()2=1×( 2R-1),由此得2R=3,所以AB=3.
故答案是:3.
【点睛】考查了垂径定理、勾股定理或相交弦定理.
18.8
【分析】作OM⊥AB于M,ON⊥CD于N,连接OA、OC,根据垂径定理得到
根据AB∥CD,得到点M、O、N在同一条直线上,在Rt△AOM中,根据勾股定理求出
进而求出ON,在Rt△CON中,根据勾股定理求出根据垂径定理即可求出弦CD的长.
【详解】作OM⊥AB于M,ON⊥CD于N,连接OA、OC,
则
∵AB∥CD,
∴点M、O、N在同一条直线上,
在Rt△AOM中,
∴ON=MN﹣OM=3,
在Rt△CON中,
∵ON⊥CD,
∴CD=2CN=8.
【点睛】考查勾股定理以及垂径定理,作出辅助线,构造直角三角形是解题的关键.
19.证明见解析
【详解】试题分析:根据等腰三角形的性质由OC=OD得∠OCD=∠ODC,由OA=OB得∠A=∠B,再根据三角形外角性质得∠OCD=∠A+∠AOC,∠ODC=∠B+∠BOD,利用等量代换得到∠AOC=∠BOD,然后根据在同圆和等圆中,相等的圆心角所对的弧相等即可得到结论.
证明:∵OC=OD,∴∠OCD=∠ODC.
∵AO=OB,∴∠A=∠B.
∴∠OCD-∠A=∠ODC-∠B,
即∠AOC=∠BOD,
即∠AOE=∠BOF.∴=.
点睛:本题考查了圆心角、弧、弦的关系:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
20.(1)证明见解析;(2),,,.
【分析】(1)连接AD后,证明这两条弧所对的圆周角相等,即,该题得证;
(2)由这两条弧度数之比为4:5,分别求出它们的度数,再根据 ,求出和的度数,即可求出 和,利用圆的内接四边形对角互补可以得到另外两个内角的度数.
【详解】解:(1)如图,连结,
∵是直径,
∴,
∵,
∴,
∴.
(2)∵,与的度数之比为,
∴,,
∵,∴,
∴,
∴,,
∵,,
∴,,
∴,,,.
【点睛】本题考查了圆中的弧和圆周角之间的关系,学生应在理解圆周角定理以及其推论的同时,能熟练应用它们,解决本题的关键是通过连线,构造两弧所对的圆周角,通过角的关系来证明弧的关系,同时应明白圆周角等于其所对弧的度数的二分之一,能由弧度求出角度,只有牢牢记住它们的关系,才能灵活地在角与弧之间进行转化,求出答案.
21.
【分析】根据题意和垂径定理得到,根据勾股定理求得半径,进而利用勾股定理求得,即可求得.
【详解】设于交于G,与交于H,
∵,
∴,
设圆拱的半径为r,
在中,,
∴,
解得,
∴,
∴,
在中,,
∴,
解得,
∴,
∴.
【点睛】本题考查了垂径定理的应用,作出辅助线构建直角三角形,利用勾股定理求解是解题的关键.
22.DB=cm
【分析】由AB是⊙O的直径,弦CD⊥AB,根据垂径定理,可得CE=DE,∠AEC=∠DEB=90°,然后由含30°角的直角三角形的性质,即可求得EC与DE的长,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可求得∠B=30°,继而求得DB的长.
【详解】∵AB是⊙O的直径,弦CD⊥AB,
∴CE=DE,∠AEC=∠DEB=90°,
∵∠B=∠ACD=30°,
在Rt△ACE中,AC=2AE=4cm,
∴CE==2(cm),
∴DE=2cm,
在Rt△BDE中,∠B=30°,
∴BD=2DE=4cm.
∴DB的长为4cm.
【点睛】本题考查了垂径定理,在同圆或等圆中同弧或等弧所对的圆周角相等,含30°角直角三角形的性质及勾股定理,其中含30°角直角三角形的性质是解题的关键.
23.见解析
【分析】连接OC,利用HL可证明△ODB≌△EDC,可得∠DOC=∠EOC,根据在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等即可证明,可得点C是的中点.
【详解】连接OC,
∵CD=CE,OC=OC,CD⊥OA,CE⊥OB,
∴△ODB≌△EDC(HL),
∴∠DOC=∠EOC,
∵∠DOC与∠EOC分别是和所对的圆心角,
∴,
∴点C是的中点.
【点睛】此题主要考查了全等三角形的判定与性质及圆心角、弧、弦的关系,在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
24.5cm
【分析】首先连接OA,根据垂径定理可得CD⊥AB,AE=4,根据勾股定理求出OA的长度.
【详解】连接OA,CD为直径,且CD平分AB于E,
∴CD⊥AB,AE=AB=4cm,
在Rt△OAE中,
∴⊙O的半径为5cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
