2.5直线与圆的位置关系暑假预习练(含解析) 苏科版数学九年级上册
文档属性
| 名称 | 2.5直线与圆的位置关系暑假预习练(含解析) 苏科版数学九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-09 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2.5直线与圆的位置关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
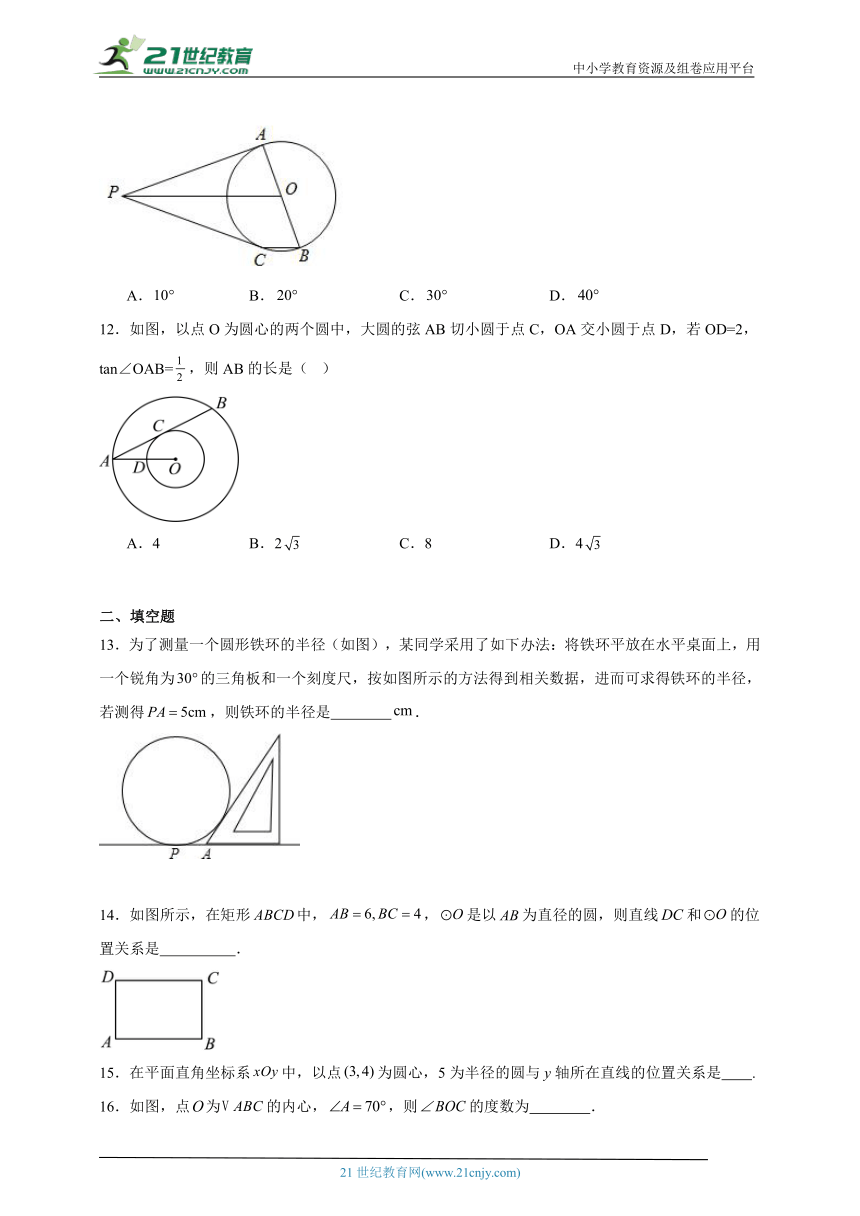
1.如图,在△ABC中,∠ACB=90°,点O在AC上,以O为圆心,OC为半径作⊙O,过点A作AD⊥BO交BO的延长线于点D.则下列结论中:①点A、B、C、D在同一个圆上;②∠ABC=2∠CAD;③若∠BOC=∠BAD,则AB与⊙O相切,正确的结论是( )
A.①②③ B.①② C.②③ D.①③
2.如图,、分别与相切于A、B两点,点C为上一点,连接、,若,则的度数为( )
A. B. C. D.
3.如图,已知圆O是的内切圆,且,则的度数是( )
A. B. C. D.
4.如图所示,是的外接圆,为的直径,过点作的切线,交的延长线于点D.若,则的度数是( )
A. B. C. D.
5.若⊙O的半径为R,直线l与⊙O有公共点,若圆心到直线l的距离为d,则d与R的大小关系是( ).
A.d>R B.d<R C.d≥R D.d≤R
6.在Rt△ABC中,∠C=90°,AC=6cm,则以A为圆心6cm为半径的圆与直线BC的位置关系是( )
A.相离 B.相切 C.相交 D.外离
7.已知直线与⊙O相离,如果⊙O的半径为R,点O到直线的距离为d,那么( )
A.d>R B.d8.如图,在平面直角坐标系中,点在直线上,其中,.与轴正半轴相切的与直线相交于、两点,若,则的值为( )
A.1 B.1.5 C.2 D.2.5
9.在平面直角坐标系xOy中,以点(-3,4)为圆心,4为半径的圆( )
A.与x轴相交,与y轴相切 B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交 D.与x轴相切,与y轴相离
10.若⊙O的半径为R,点O到直线l的距离为d,且d与R是方程x -4x+m=0的两根,且直线l与⊙O 相切,则m的值为( )
A.1 B.2 C.3 D.4
11.如图,AB是的直径,PA与相切于点A,交于点C.若,则的度数为( )
A. B. C. D.
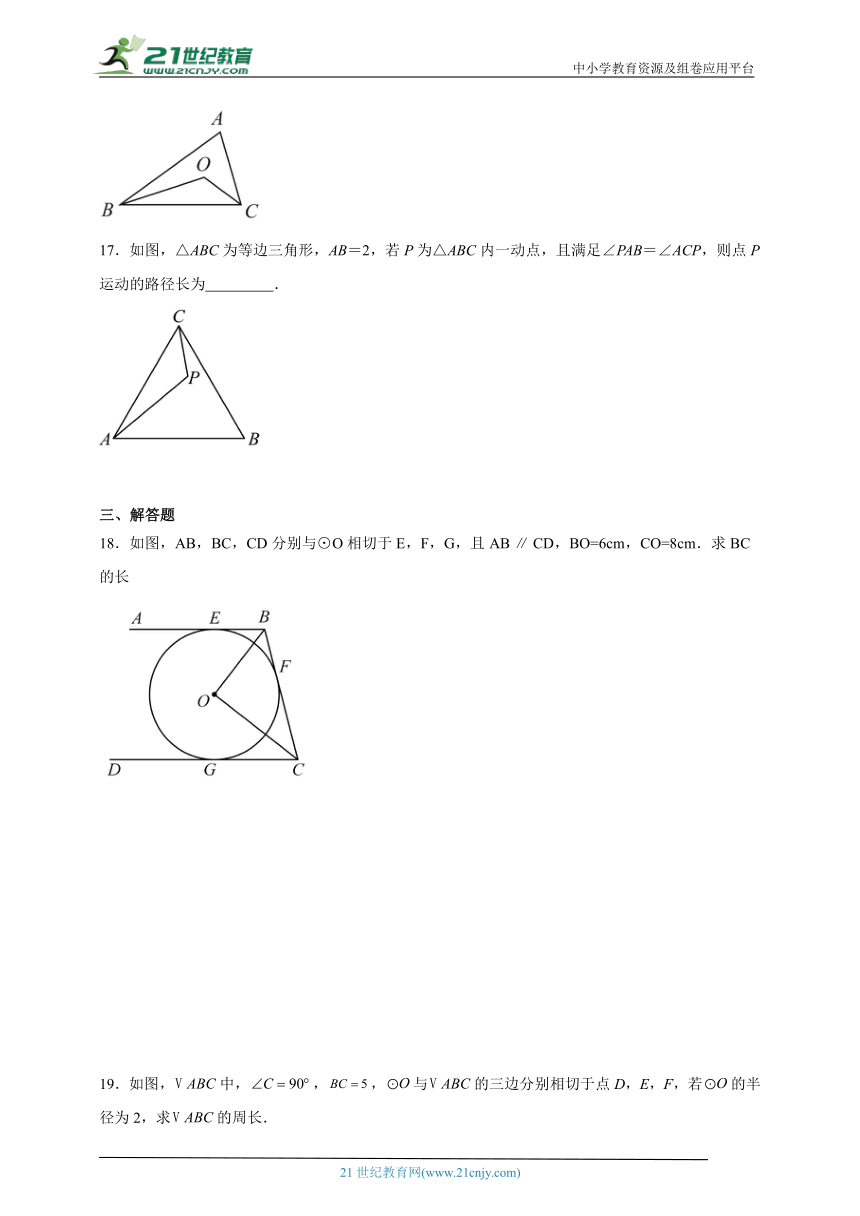
12.如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=,则AB的长是( )
A.4 B.2 C.8 D.4
二、填空题
13.为了测量一个圆形铁环的半径(如图),某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径,若测得,则铁环的半径是 .
14.如图所示,在矩形中,,是以为直径的圆,则直线和的位置关系是 .
15.在平面直角坐标系中,以点为圆心,5为半径的圆与y轴所在直线的位置关系是 .
16.如图,点为的内心,,则的度数为 .
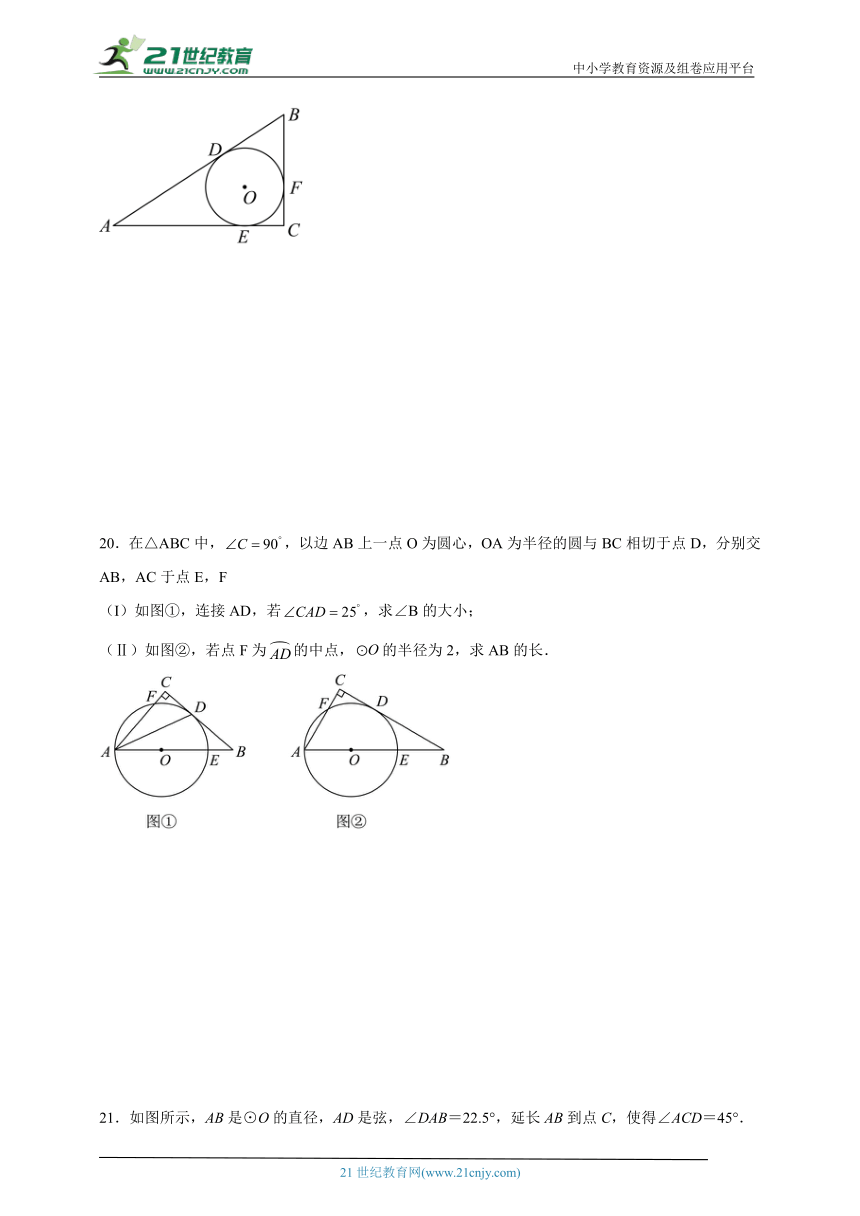
17.如图,△ABC为等边三角形,AB=2,若P为△ABC内一动点,且满足∠PAB=∠ACP,则点P运动的路径长为 .
三、解答题
18.如图,AB,BC,CD分别与⊙O相切于E,F,G,且AB ∥ CD,BO=6cm,CO=8cm.求BC的长
19.如图,中,,,与的三边分别相切于点D,E,F,若的半径为2,求的周长.
20.在△ABC中,,以边AB上一点O为圆心,OA为半径的圆与BC相切于点D,分别交AB,AC于点E,F
(I)如图①,连接AD,若,求∠B的大小;
(Ⅱ)如图②,若点F为的中点,的半径为2,求AB的长.
21.如图所示,AB是⊙O的直径,AD是弦,∠DAB=22.5°,延长AB到点C,使得∠ACD=45°.
(1)求证:CD是⊙O的切线;
(2)若AB=2,求BC的长.
22.如图,内接于,是的直径,点D是上一点,连接、,过点B作,交的延长线于点E,平分.
(1)求证:是的切线;
(2)若,的半径为6,求的长.
23.如图,在平面直角坐标系xOy中,点P(a,b)在第一象限.以P为圆心的圆经过原点,与y轴的另一个交点为A.点Q是线段OA上的点(不与O,A重合),过点Q作PQ的垂线交⊙P于点B(m,n),其中m≥0.
(1)若b=5,则点A坐标是 ;
(2)在(1)的条件下,若OQ=8,求线段BQ的长;
(3)若点P在函数y=x2(x>0)的图象上,△BQP是等腰三角形且PQ=,求出点B的坐标.
24.如图,已知是锐角三角形.
(1)请在图1中用无刻度的直尺和圆规作图;作直线,使上的各点到、两点的距离相等;设直线与、分别交于点、,作一个圆,使得圆心在线段上,且与边、相切;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若,,则的半径为________.
《2.5直线与圆的位置关系》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C C C D B A C C D
题号 11 12
答案 B C
1.D
【分析】由∠D=90°=∠ACB,得出点A、B、C、D在同一个圆上,①正确;证出∠OBC=∠CAD,当BD是∠ABC平分线时,∠ABC=2∠CAD,②错误;若∠BOC=∠BAD,则∠OBC=∠ABD,作OE⊥AB于E,由角平分线性质得出OE=OC,得出AB与⊙O相切,③正确;即可得出结论.
【详解】解:∵AD⊥BO,
∴∠D=90°=∠ACB,
∴点A、B、C、D在同一个圆上,①正确;
∵∠ACB=∠D=90°,∠BOC=∠AOD,
∴∠OBC=∠CAD,
当BD是∠ABC平分线时,∠ABC=2∠CAD,②错误;
若∠BOC=∠BAD,
∵∠ACB=∠D=90°,
∴∠OBC=∠ABD,
作OE⊥AB于E,如图所示:
则OE=OC,
∴AB与⊙O相切,③正确;
故选D.
【点睛】本题考查了直角三角形的性质、点与圆的位置关系、切线的判定、角平分线的性质等知识;掌握直角三角形的性质和切线的判定是解题的关键.
2.C
【分析】先利用切线的性质得,再利用四边形的内角和计算出的度数,然后根据圆周角定理计算的度数.
【详解】解:如图,连接,
∵、分别与相切于A,B两点,
∴,,
∴,
∴,
∴.
故选C
【点睛】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理,掌握以上知识是解本题的关键.
3.C
【分析】由三角形内切定义可知是的角平分线,所以可得到关系式,把对应数值代入即可求得的值.
【详解】解:∵O是的内切圆,
∴是的角平分线,
∴
,
∴.
故选:C.
【点睛】此题主要考查了三角形的内切圆,以及三角形的角平分线.关键是要知道内切圆的圆心是三个角平分线的交点.
4.C
【分析】连接,根据切线的性质得到,根据圆周角定理求出,根据直角三角形的性质计算得到答案.
【详解】解:连接,
为的切线,
.
,
,
.
故选:C.
【点睛】本题主要考查了切线的性质、圆周角定理、直角三角形的性质,掌握圆的切线垂直于经过切点的半径是解题的关键.
5.D
【分析】直线l与⊙O有公共点,则可得圆与直线相交或相切,根据圆和直线的位置关系,可以得出d与R的大小关系.
【详解】∵直线l与⊙O有公共点,
∴直线l与⊙O相交或相切.
∵圆心到直线l的距离是d,
∴可得d≤R.
故选D.
【点睛】本题考查了直线与圆的位置关系的知识,解决本题的关键是熟记位置关系及名称. 在判断直线与圆的位置关系时,通常要得到圆心到直线的距离d和圆的半径r,然后再利用d与r的大小关系进行判断.直线与圆的位置关系:①当d>r时,直线与圆相离;②当d=r时,直线与圆相切;③当d<r时,直线与圆相交.
6.B
【详解】根据题意得:点A到直线BC的距离=AC,
∵AC=6cm,圆的半径=6cm,
∴以A为圆心6cm为半径的圆与直线BC相切.
故选B.
7.A
【分析】直线与圆的位置关系:①当d>r时,直线与圆相离;②当d=r时,直线与圆相切;③当d<r时,直线与圆相交;
【详解】由于直线与☉O相离,
∴d>r.
故选A.
【点睛】本题涉及的知识点是直线与圆的位置关系的判定;
在判断直线与圆的位置关系时,通常要得到圆心到直线的距离,然后再利用d与r的大小关系进行判断.
直线与圆的位置关系:
①当d>r时,直线与圆相离;
②当d=r时,直线与圆相切;
③当d<r时,直线与圆相交.
8.C
【分析】如图,设与y轴切于点C,连接MC,则MC⊥y轴,于是半径MC可求,即为点M的横坐标m,进一步即得结果.
【详解】解:如图,设与y轴切于点C,连接MC,则MC⊥y轴,,
当m=1时,.
故选:C.
【点睛】本题考查了圆的切线的性质和一次函数图象上点的坐标特征,属于常考题型,熟练掌握直线和圆相切的性质是解题关键.
9.C
【详解】分析:首先画出图形,根据点的坐标得到圆心到X轴的距离是4,到Y轴的距离是3,根据直线与圆的位置关系即可求出答案.
解答:解:圆心到X轴的距离是4,到y轴的距离是3,
4=4,3<4,
∴圆与x轴相切,与y轴相交,
故选C.
10.D
【分析】先根据直线与圆的位置关系得出方程有两个相等的根,再根据△=0即可求出m的值.
【详解】∵d、R是方程x2-4x+m=0的两个根,且直线L与⊙O相切,
∴d=R,
∴方程有两个相等的实根,
∴△=16-4m=0,
解得,m=4,
故选D.
【点睛】本题考查的是直线与圆的位置关系及一元二次方程根的判别式,熟知以上知识是解答此题的关键.
11.B
【分析】连接OC,证明△PAO≌△PCO(SAS),得到∠OCP=90°,进而求得.
【详解】
如图,连接OC,
因为OB=OC,
所以∠OCB=∠OBC=70°,
所以∠BOC=180°-70°-70°=40°,
又因为,
所以∠AOP=∠B=70°,
∴∠POC=180°-∠AOP-∠BOC=70°,
所以在△PAO和△PCO中,
,
所以△PAO≌△PCO(SAS),
所以∠OCP=∠OAP
因为PA与相切于点A,
所以∠OCP=∠OAP=90°,
所以∠OPC=180°-∠POC-∠OCP=20°,
故选:B.
【点睛】本题考查了圆的切线、证明全等三角形和平行线等知识内容,灵活运用条件,学会选择辅助线是解题的关键.
12.C
【详解】试题解析:连接OC,
∵大圆的弦AB切小圆于点 C,
∴OC⊥AB,
∴AB=2AC,
∵OD=2,
∴OC=2,
∵tan∠OAB=,
∴AC=4,
∴AB=8,
故选C.
考点:切线的性质.
13.
【分析】取圆的圆心为O,三角板与圆相切的切点为Q,连OA,OP,OQ,由切线性质知△OPA为直角三角形,从而在Rt△OPA中由勾股定理易求得半径.
【详解】解:设铁环的圆心为O,三角板与圆相切的切点为Q,连接OP、OA,
∵AP为⊙O的切线,AQ也为⊙O的切线,
∴AO为∠PAQ的平分线,即∠PAO=∠QAO,
又∠BAC=60°,∠PAO+∠QAO+∠BAC=180°,
∴∠PAO=∠QAO=60°,
在Rt△OPA中,PA=5,∠POA=30°,
∴OA=10,,
故答案为:.
【点睛】本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,构造直角三角形解决有关问题.
14.相离
【分析】首先要明确圆心到直线的距离和圆的半径;再根据直线和圆的位置关系与数量之间的联系进行分析即可.
【详解】根据题意,得圆心到直线的距离等于,圆的半径是,
∴圆心到直线的距离大于半径,得直线和圆相离.
故答案为:相离.
【点睛】此题主要考查了直线与圆的位置关系,能够熟练根据数量关系判断直线和圆的位置关系是解题关键.
15.相交
【分析】本题可先求出圆心到y轴的距离,再根据半径比较.
【详解】圆心到y轴的距离是3<5,
则圆的y轴所在直线的位置关系是相交.
故答案是:相交.
【点睛】此题考查的是圆与直线的关系,即圆心到直线的距离大于圆心距,直线与圆相离;小于圆心距,直线与圆相交;等于圆心距,则直线与圆相切.
16./125度
【分析】利用内心的性质得出,,进而利用三角形内角和定理得出,进而求出答案.
【详解】解:∵O是的内心,
∴,,
∵,
∴,
∴,
∴.
故答案为.
【点睛】此题主要考查了三角形内心的性质以及三角形内角和定理,正确得出是解题关键.
17.
【详解】解:∵△ABC是等边三角形,
∴∠ABC=∠BAC=60°,AC=AB=2,
∵∠PAB=∠ACP,
∴∠PAC+∠ACP=60°,
∴∠APC=120°,
∴点P的运动轨迹是,如图所示:
连接OA、OC,作OD⊥AC于D,
则AD=CDAC=1,
∵所对的圆心角=2∠APC=240°,
∴劣弧AC所对的圆心角∠AOC=360°﹣240°=120°,
∵OA=OC,
∴∠OAD=30°,
∵OD⊥AC,
∴ODAD,OA=2OD,
∴的长为π;
故答案为:π.
18.10cm.
【详解】试题分析:根据切线长定理和平行线的性质定理得到△BOC是直角三角形.再根据勾股定理求出BC的长.
试题解析:∵AB,BC,CD分别与⊙O相切于E,F,G;
∴∠CBO=∠ABC,∠BCO=∠DCB,
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴∠CBO+∠BCO=∠ABC+∠DCB=(∠ABC+∠DCB)=90°.
∴BC=cm.
考点: 切割线定理.
19.30
【分析】本题考查的是三角形的内切圆与内心,根据题意作出辅助线,利用勾股定理求解是解答此题的关键.
设,由切线长定理得,根据题意可得四边形为正方形,则,,在直角三角形中,利用勾股定理求出x,然后求其周长.
【详解】解:连接,,设.
由切线长定理,得.
与的三边分别切于点D,E,F,
,,
∵
∴四边形为正方形.
的半径为2,,
,.
在中,,
即,
解得,
,,
的周长为.
20.(1)∠B=40°;(2)AB= 6.
【分析】(1)连接OD,由在△ABC中, ∠C=90°,BC是切线,易得AC∥OD ,即可求得∠CAD=∠ADO ,继而求得答案;
(2)首先连接OF,OD,由AC∥OD得∠OFA=∠FOD ,由点F为弧AD的中点,易得△AOF是等边三角形,继而求得答案.
【详解】解:(1)如解图①,连接OD,
∵BC切⊙O于点D,
∴∠ODB=90°,
∵∠C=90°,
∴AC∥OD,
∴∠CAD=∠ADO,
∵OA=OD,
∴∠DAO=∠ADO=∠CAD=25°,
∴∠DOB=∠CAO=∠CAD+∠DAO=50°,
∵∠ODB=90°,
∴∠B=90°-∠DOB=90°-50°=40°;
(2)如解图②,连接OF,OD,
∵AC∥OD,
∴∠OFA=∠FOD,
∵点F为弧AD的中点,
∴∠AOF=∠FOD,
∴∠OFA=∠AOF,
∴AF=OA,
∵OA=OF,
∴△AOF为等边三角形,
∴∠FAO=60°,则∠DOB=60°,
∴∠B=30°,
∵在Rt△ODB中,OD=2,
∴OB=4,
∴AB=AO+OB=2+4=6.
【点睛】本题考查了切线的性质,平行线的性质,等腰三角形的性质,弧弦圆心角的关系,等边三角形的判定与性质,含30°角的直角三角形的性质.熟练掌握切线的性质是解(1)的关键,证明△AOF为等边三角形是解(2)的关键.
21.(1)见解析
(2)
【分析】(1)连接DO,由三角形的外角性质易得∠DOC=∠C=45°,故有∠ODC=90°,即CD是圆的切线.
(2)利用等腰直角三角形的性质求解即可.
【详解】(1)证明:连接DO,
∵AO=DO,
∴∠DAO=∠ADO=22.5°.
∴∠DOC=45°.
又∵∠ACD=∠DOC=45°.
∴∠ODC=90°.
又∵OD是⊙O的半径,
∴CD是⊙O的切线.
(2)解:连接DB,
∵直径,△OCD为等腰直角三角形,
∴,,
∴.
【点睛】本题利用了等边对等角,三角形的外角与内角的关系,切线的概念,勾股定理,熟记各知识点并熟练应用是解题的关键.
22.(1)见解析
(2)
【分析】本题考查切线的判定定理,等边三角形的判定及性质,所对的直角边等于斜边的一半,勾股定理,解题的关键是熟练掌握以上知识点.
(1)连接,求出即可;
(2)证明是等边三角形,利用所对的直角边等于斜边的一半得到,再由勾股定理,进行求解即可.
【详解】(1)证明:连接.
∵,
∴.
∵平分,
∴,
∴.
∴,
∴,即,
又∵是的半径,
∴是的切线.
(2)解:,
∴.
又∵,
∴是等边三角形,
∴,,
∴,
∴.
由勾股定理,得.
23.(1)(0,10);(2)4;(3)B点坐标为(,6+)或(,2﹣).
【分析】(1)过点P作PH⊥OA于点H,由垂径定理可求出OA的长,进而可求出A的坐标;
(2)连接BP、OP,由已知条件易求QH,在Rt△QHP中,由勾股定理可得:PQ2=QH2+PH2=9+PH2,在Rt△PHO中,由勾股定理可得:PO2=OH2+PH2=25+PH2=BP2,进而在Rt△BQP中,BQ2=BP2-PQ2=(25+PH2)-(9+PH2)=16.所以BQ=4;
(3)已知线段PQ的长度可以为,作BM⊥y轴于点M,首先求出a=2,再求出MQ=PH=2,利用勾股定理可求出MB=QH=.所以可得:B1(,6+),若点Q在OH上,再由抛物线对称性可得B2(,2-)综上,综上,当PQ=时,B点坐标为(,6+)或(,2﹣).
【详解】(1)过点P作PH⊥OA于点H,
∴OA=2OH,
∵b=5,
∴OH=5,
∴OA=10,
∴点A坐标是(0,10).
故答案为(0,10).
(2)连接BP、OP.
∵b=5,PH⊥OA,
∴OH=AH=5.
∵OQ=8,
∴QH=OQ﹣OH=3.
在Rt△QHP中,PQ2=QH2+PH2=9+PH2,
在RtPHO中,PO2=OH2+PH2=25+PH2=BP2,
在RtBQP中,BQ2=BP2﹣PQ2=(25+PH2)﹣(9+PH2)=16.
∴BQ=4.
(3)∵△BQP是等腰直角三角形,PQ=,
∴半径BP=2.
又∵P(a,a2),
∴OP2=a2+a4=(2)2.
即a4+a2﹣20=0.
解得a=±2.
∵a>0
∴a=2.
∴P(2,4).
如图,作BM⊥y轴于点M,则△QBM≌△PQH.
∴MQ=PH=2,
∴MB=QH=.
∴B1(,6+).
若点Q在OH上,由对称性可得B2(,2﹣)
综上,当PQ=时,B点坐标为(,6+)或(,2﹣).
24.(1)见解析;(2)
【分析】(1)由题意知直线为线段BC的垂直平分线,若圆心在线段上,且与边、相切,则再作出的角平分线,与MN的交点即为圆心O;
(2)过点作,垂足为,根据即可求解.
【详解】解:(1)①先作的垂直平分线:分别以B,C为圆心,大于的长为半径画弧,连接两个交点即为直线l,分别交、于、;
②再作的角平分线:以点B为圆心,任意长为半径作圆弧,与的两条边分别有一个交点,再以这两个交点为圆心,相同长度为半径作弧,连接这两条弧的交点与点B,即为的角平分线,这条角平分线与线段MN的交点即为;
③以为圆心,为半径画圆,圆即为所求;
(2)过点作,垂足为,设
∵,,∴,∴
根据面积法,∴
∴,解得,
故答案为:.
【点睛】本题考查了尺规作图,切线的性质等内容,解题的关键是掌握线段垂直平分线、角平分线的尺规作图.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.5直线与圆的位置关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在△ABC中,∠ACB=90°,点O在AC上,以O为圆心,OC为半径作⊙O,过点A作AD⊥BO交BO的延长线于点D.则下列结论中:①点A、B、C、D在同一个圆上;②∠ABC=2∠CAD;③若∠BOC=∠BAD,则AB与⊙O相切,正确的结论是( )
A.①②③ B.①② C.②③ D.①③
2.如图,、分别与相切于A、B两点,点C为上一点,连接、,若,则的度数为( )
A. B. C. D.
3.如图,已知圆O是的内切圆,且,则的度数是( )
A. B. C. D.
4.如图所示,是的外接圆,为的直径,过点作的切线,交的延长线于点D.若,则的度数是( )
A. B. C. D.
5.若⊙O的半径为R,直线l与⊙O有公共点,若圆心到直线l的距离为d,则d与R的大小关系是( ).
A.d>R B.d<R C.d≥R D.d≤R
6.在Rt△ABC中,∠C=90°,AC=6cm,则以A为圆心6cm为半径的圆与直线BC的位置关系是( )
A.相离 B.相切 C.相交 D.外离
7.已知直线与⊙O相离,如果⊙O的半径为R,点O到直线的距离为d,那么( )
A.d>R B.d
A.1 B.1.5 C.2 D.2.5
9.在平面直角坐标系xOy中,以点(-3,4)为圆心,4为半径的圆( )
A.与x轴相交,与y轴相切 B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交 D.与x轴相切,与y轴相离
10.若⊙O的半径为R,点O到直线l的距离为d,且d与R是方程x -4x+m=0的两根,且直线l与⊙O 相切,则m的值为( )
A.1 B.2 C.3 D.4
11.如图,AB是的直径,PA与相切于点A,交于点C.若,则的度数为( )
A. B. C. D.
12.如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=,则AB的长是( )
A.4 B.2 C.8 D.4
二、填空题
13.为了测量一个圆形铁环的半径(如图),某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径,若测得,则铁环的半径是 .
14.如图所示,在矩形中,,是以为直径的圆,则直线和的位置关系是 .
15.在平面直角坐标系中,以点为圆心,5为半径的圆与y轴所在直线的位置关系是 .
16.如图,点为的内心,,则的度数为 .
17.如图,△ABC为等边三角形,AB=2,若P为△ABC内一动点,且满足∠PAB=∠ACP,则点P运动的路径长为 .
三、解答题
18.如图,AB,BC,CD分别与⊙O相切于E,F,G,且AB ∥ CD,BO=6cm,CO=8cm.求BC的长
19.如图,中,,,与的三边分别相切于点D,E,F,若的半径为2,求的周长.
20.在△ABC中,,以边AB上一点O为圆心,OA为半径的圆与BC相切于点D,分别交AB,AC于点E,F
(I)如图①,连接AD,若,求∠B的大小;
(Ⅱ)如图②,若点F为的中点,的半径为2,求AB的长.
21.如图所示,AB是⊙O的直径,AD是弦,∠DAB=22.5°,延长AB到点C,使得∠ACD=45°.
(1)求证:CD是⊙O的切线;
(2)若AB=2,求BC的长.
22.如图,内接于,是的直径,点D是上一点,连接、,过点B作,交的延长线于点E,平分.
(1)求证:是的切线;
(2)若,的半径为6,求的长.
23.如图,在平面直角坐标系xOy中,点P(a,b)在第一象限.以P为圆心的圆经过原点,与y轴的另一个交点为A.点Q是线段OA上的点(不与O,A重合),过点Q作PQ的垂线交⊙P于点B(m,n),其中m≥0.
(1)若b=5,则点A坐标是 ;
(2)在(1)的条件下,若OQ=8,求线段BQ的长;
(3)若点P在函数y=x2(x>0)的图象上,△BQP是等腰三角形且PQ=,求出点B的坐标.
24.如图,已知是锐角三角形.
(1)请在图1中用无刻度的直尺和圆规作图;作直线,使上的各点到、两点的距离相等;设直线与、分别交于点、,作一个圆,使得圆心在线段上,且与边、相切;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若,,则的半径为________.
《2.5直线与圆的位置关系》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C C C D B A C C D
题号 11 12
答案 B C
1.D
【分析】由∠D=90°=∠ACB,得出点A、B、C、D在同一个圆上,①正确;证出∠OBC=∠CAD,当BD是∠ABC平分线时,∠ABC=2∠CAD,②错误;若∠BOC=∠BAD,则∠OBC=∠ABD,作OE⊥AB于E,由角平分线性质得出OE=OC,得出AB与⊙O相切,③正确;即可得出结论.
【详解】解:∵AD⊥BO,
∴∠D=90°=∠ACB,
∴点A、B、C、D在同一个圆上,①正确;
∵∠ACB=∠D=90°,∠BOC=∠AOD,
∴∠OBC=∠CAD,
当BD是∠ABC平分线时,∠ABC=2∠CAD,②错误;
若∠BOC=∠BAD,
∵∠ACB=∠D=90°,
∴∠OBC=∠ABD,
作OE⊥AB于E,如图所示:
则OE=OC,
∴AB与⊙O相切,③正确;
故选D.
【点睛】本题考查了直角三角形的性质、点与圆的位置关系、切线的判定、角平分线的性质等知识;掌握直角三角形的性质和切线的判定是解题的关键.
2.C
【分析】先利用切线的性质得,再利用四边形的内角和计算出的度数,然后根据圆周角定理计算的度数.
【详解】解:如图,连接,
∵、分别与相切于A,B两点,
∴,,
∴,
∴,
∴.
故选C
【点睛】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理,掌握以上知识是解本题的关键.
3.C
【分析】由三角形内切定义可知是的角平分线,所以可得到关系式,把对应数值代入即可求得的值.
【详解】解:∵O是的内切圆,
∴是的角平分线,
∴
,
∴.
故选:C.
【点睛】此题主要考查了三角形的内切圆,以及三角形的角平分线.关键是要知道内切圆的圆心是三个角平分线的交点.
4.C
【分析】连接,根据切线的性质得到,根据圆周角定理求出,根据直角三角形的性质计算得到答案.
【详解】解:连接,
为的切线,
.
,
,
.
故选:C.
【点睛】本题主要考查了切线的性质、圆周角定理、直角三角形的性质,掌握圆的切线垂直于经过切点的半径是解题的关键.
5.D
【分析】直线l与⊙O有公共点,则可得圆与直线相交或相切,根据圆和直线的位置关系,可以得出d与R的大小关系.
【详解】∵直线l与⊙O有公共点,
∴直线l与⊙O相交或相切.
∵圆心到直线l的距离是d,
∴可得d≤R.
故选D.
【点睛】本题考查了直线与圆的位置关系的知识,解决本题的关键是熟记位置关系及名称. 在判断直线与圆的位置关系时,通常要得到圆心到直线的距离d和圆的半径r,然后再利用d与r的大小关系进行判断.直线与圆的位置关系:①当d>r时,直线与圆相离;②当d=r时,直线与圆相切;③当d<r时,直线与圆相交.
6.B
【详解】根据题意得:点A到直线BC的距离=AC,
∵AC=6cm,圆的半径=6cm,
∴以A为圆心6cm为半径的圆与直线BC相切.
故选B.
7.A
【分析】直线与圆的位置关系:①当d>r时,直线与圆相离;②当d=r时,直线与圆相切;③当d<r时,直线与圆相交;
【详解】由于直线与☉O相离,
∴d>r.
故选A.
【点睛】本题涉及的知识点是直线与圆的位置关系的判定;
在判断直线与圆的位置关系时,通常要得到圆心到直线的距离,然后再利用d与r的大小关系进行判断.
直线与圆的位置关系:
①当d>r时,直线与圆相离;
②当d=r时,直线与圆相切;
③当d<r时,直线与圆相交.
8.C
【分析】如图,设与y轴切于点C,连接MC,则MC⊥y轴,于是半径MC可求,即为点M的横坐标m,进一步即得结果.
【详解】解:如图,设与y轴切于点C,连接MC,则MC⊥y轴,,
当m=1时,.
故选:C.
【点睛】本题考查了圆的切线的性质和一次函数图象上点的坐标特征,属于常考题型,熟练掌握直线和圆相切的性质是解题关键.
9.C
【详解】分析:首先画出图形,根据点的坐标得到圆心到X轴的距离是4,到Y轴的距离是3,根据直线与圆的位置关系即可求出答案.
解答:解:圆心到X轴的距离是4,到y轴的距离是3,
4=4,3<4,
∴圆与x轴相切,与y轴相交,
故选C.
10.D
【分析】先根据直线与圆的位置关系得出方程有两个相等的根,再根据△=0即可求出m的值.
【详解】∵d、R是方程x2-4x+m=0的两个根,且直线L与⊙O相切,
∴d=R,
∴方程有两个相等的实根,
∴△=16-4m=0,
解得,m=4,
故选D.
【点睛】本题考查的是直线与圆的位置关系及一元二次方程根的判别式,熟知以上知识是解答此题的关键.
11.B
【分析】连接OC,证明△PAO≌△PCO(SAS),得到∠OCP=90°,进而求得.
【详解】
如图,连接OC,
因为OB=OC,
所以∠OCB=∠OBC=70°,
所以∠BOC=180°-70°-70°=40°,
又因为,
所以∠AOP=∠B=70°,
∴∠POC=180°-∠AOP-∠BOC=70°,
所以在△PAO和△PCO中,
,
所以△PAO≌△PCO(SAS),
所以∠OCP=∠OAP
因为PA与相切于点A,
所以∠OCP=∠OAP=90°,
所以∠OPC=180°-∠POC-∠OCP=20°,
故选:B.
【点睛】本题考查了圆的切线、证明全等三角形和平行线等知识内容,灵活运用条件,学会选择辅助线是解题的关键.
12.C
【详解】试题解析:连接OC,
∵大圆的弦AB切小圆于点 C,
∴OC⊥AB,
∴AB=2AC,
∵OD=2,
∴OC=2,
∵tan∠OAB=,
∴AC=4,
∴AB=8,
故选C.
考点:切线的性质.
13.
【分析】取圆的圆心为O,三角板与圆相切的切点为Q,连OA,OP,OQ,由切线性质知△OPA为直角三角形,从而在Rt△OPA中由勾股定理易求得半径.
【详解】解:设铁环的圆心为O,三角板与圆相切的切点为Q,连接OP、OA,
∵AP为⊙O的切线,AQ也为⊙O的切线,
∴AO为∠PAQ的平分线,即∠PAO=∠QAO,
又∠BAC=60°,∠PAO+∠QAO+∠BAC=180°,
∴∠PAO=∠QAO=60°,
在Rt△OPA中,PA=5,∠POA=30°,
∴OA=10,,
故答案为:.
【点睛】本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,构造直角三角形解决有关问题.
14.相离
【分析】首先要明确圆心到直线的距离和圆的半径;再根据直线和圆的位置关系与数量之间的联系进行分析即可.
【详解】根据题意,得圆心到直线的距离等于,圆的半径是,
∴圆心到直线的距离大于半径,得直线和圆相离.
故答案为:相离.
【点睛】此题主要考查了直线与圆的位置关系,能够熟练根据数量关系判断直线和圆的位置关系是解题关键.
15.相交
【分析】本题可先求出圆心到y轴的距离,再根据半径比较.
【详解】圆心到y轴的距离是3<5,
则圆的y轴所在直线的位置关系是相交.
故答案是:相交.
【点睛】此题考查的是圆与直线的关系,即圆心到直线的距离大于圆心距,直线与圆相离;小于圆心距,直线与圆相交;等于圆心距,则直线与圆相切.
16./125度
【分析】利用内心的性质得出,,进而利用三角形内角和定理得出,进而求出答案.
【详解】解:∵O是的内心,
∴,,
∵,
∴,
∴,
∴.
故答案为.
【点睛】此题主要考查了三角形内心的性质以及三角形内角和定理,正确得出是解题关键.
17.
【详解】解:∵△ABC是等边三角形,
∴∠ABC=∠BAC=60°,AC=AB=2,
∵∠PAB=∠ACP,
∴∠PAC+∠ACP=60°,
∴∠APC=120°,
∴点P的运动轨迹是,如图所示:
连接OA、OC,作OD⊥AC于D,
则AD=CDAC=1,
∵所对的圆心角=2∠APC=240°,
∴劣弧AC所对的圆心角∠AOC=360°﹣240°=120°,
∵OA=OC,
∴∠OAD=30°,
∵OD⊥AC,
∴ODAD,OA=2OD,
∴的长为π;
故答案为:π.
18.10cm.
【详解】试题分析:根据切线长定理和平行线的性质定理得到△BOC是直角三角形.再根据勾股定理求出BC的长.
试题解析:∵AB,BC,CD分别与⊙O相切于E,F,G;
∴∠CBO=∠ABC,∠BCO=∠DCB,
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴∠CBO+∠BCO=∠ABC+∠DCB=(∠ABC+∠DCB)=90°.
∴BC=cm.
考点: 切割线定理.
19.30
【分析】本题考查的是三角形的内切圆与内心,根据题意作出辅助线,利用勾股定理求解是解答此题的关键.
设,由切线长定理得,根据题意可得四边形为正方形,则,,在直角三角形中,利用勾股定理求出x,然后求其周长.
【详解】解:连接,,设.
由切线长定理,得.
与的三边分别切于点D,E,F,
,,
∵
∴四边形为正方形.
的半径为2,,
,.
在中,,
即,
解得,
,,
的周长为.
20.(1)∠B=40°;(2)AB= 6.
【分析】(1)连接OD,由在△ABC中, ∠C=90°,BC是切线,易得AC∥OD ,即可求得∠CAD=∠ADO ,继而求得答案;
(2)首先连接OF,OD,由AC∥OD得∠OFA=∠FOD ,由点F为弧AD的中点,易得△AOF是等边三角形,继而求得答案.
【详解】解:(1)如解图①,连接OD,
∵BC切⊙O于点D,
∴∠ODB=90°,
∵∠C=90°,
∴AC∥OD,
∴∠CAD=∠ADO,
∵OA=OD,
∴∠DAO=∠ADO=∠CAD=25°,
∴∠DOB=∠CAO=∠CAD+∠DAO=50°,
∵∠ODB=90°,
∴∠B=90°-∠DOB=90°-50°=40°;
(2)如解图②,连接OF,OD,
∵AC∥OD,
∴∠OFA=∠FOD,
∵点F为弧AD的中点,
∴∠AOF=∠FOD,
∴∠OFA=∠AOF,
∴AF=OA,
∵OA=OF,
∴△AOF为等边三角形,
∴∠FAO=60°,则∠DOB=60°,
∴∠B=30°,
∵在Rt△ODB中,OD=2,
∴OB=4,
∴AB=AO+OB=2+4=6.
【点睛】本题考查了切线的性质,平行线的性质,等腰三角形的性质,弧弦圆心角的关系,等边三角形的判定与性质,含30°角的直角三角形的性质.熟练掌握切线的性质是解(1)的关键,证明△AOF为等边三角形是解(2)的关键.
21.(1)见解析
(2)
【分析】(1)连接DO,由三角形的外角性质易得∠DOC=∠C=45°,故有∠ODC=90°,即CD是圆的切线.
(2)利用等腰直角三角形的性质求解即可.
【详解】(1)证明:连接DO,
∵AO=DO,
∴∠DAO=∠ADO=22.5°.
∴∠DOC=45°.
又∵∠ACD=∠DOC=45°.
∴∠ODC=90°.
又∵OD是⊙O的半径,
∴CD是⊙O的切线.
(2)解:连接DB,
∵直径,△OCD为等腰直角三角形,
∴,,
∴.
【点睛】本题利用了等边对等角,三角形的外角与内角的关系,切线的概念,勾股定理,熟记各知识点并熟练应用是解题的关键.
22.(1)见解析
(2)
【分析】本题考查切线的判定定理,等边三角形的判定及性质,所对的直角边等于斜边的一半,勾股定理,解题的关键是熟练掌握以上知识点.
(1)连接,求出即可;
(2)证明是等边三角形,利用所对的直角边等于斜边的一半得到,再由勾股定理,进行求解即可.
【详解】(1)证明:连接.
∵,
∴.
∵平分,
∴,
∴.
∴,
∴,即,
又∵是的半径,
∴是的切线.
(2)解:,
∴.
又∵,
∴是等边三角形,
∴,,
∴,
∴.
由勾股定理,得.
23.(1)(0,10);(2)4;(3)B点坐标为(,6+)或(,2﹣).
【分析】(1)过点P作PH⊥OA于点H,由垂径定理可求出OA的长,进而可求出A的坐标;
(2)连接BP、OP,由已知条件易求QH,在Rt△QHP中,由勾股定理可得:PQ2=QH2+PH2=9+PH2,在Rt△PHO中,由勾股定理可得:PO2=OH2+PH2=25+PH2=BP2,进而在Rt△BQP中,BQ2=BP2-PQ2=(25+PH2)-(9+PH2)=16.所以BQ=4;
(3)已知线段PQ的长度可以为,作BM⊥y轴于点M,首先求出a=2,再求出MQ=PH=2,利用勾股定理可求出MB=QH=.所以可得:B1(,6+),若点Q在OH上,再由抛物线对称性可得B2(,2-)综上,综上,当PQ=时,B点坐标为(,6+)或(,2﹣).
【详解】(1)过点P作PH⊥OA于点H,
∴OA=2OH,
∵b=5,
∴OH=5,
∴OA=10,
∴点A坐标是(0,10).
故答案为(0,10).
(2)连接BP、OP.
∵b=5,PH⊥OA,
∴OH=AH=5.
∵OQ=8,
∴QH=OQ﹣OH=3.
在Rt△QHP中,PQ2=QH2+PH2=9+PH2,
在RtPHO中,PO2=OH2+PH2=25+PH2=BP2,
在RtBQP中,BQ2=BP2﹣PQ2=(25+PH2)﹣(9+PH2)=16.
∴BQ=4.
(3)∵△BQP是等腰直角三角形,PQ=,
∴半径BP=2.
又∵P(a,a2),
∴OP2=a2+a4=(2)2.
即a4+a2﹣20=0.
解得a=±2.
∵a>0
∴a=2.
∴P(2,4).
如图,作BM⊥y轴于点M,则△QBM≌△PQH.
∴MQ=PH=2,
∴MB=QH=.
∴B1(,6+).
若点Q在OH上,由对称性可得B2(,2﹣)
综上,当PQ=时,B点坐标为(,6+)或(,2﹣).
24.(1)见解析;(2)
【分析】(1)由题意知直线为线段BC的垂直平分线,若圆心在线段上,且与边、相切,则再作出的角平分线,与MN的交点即为圆心O;
(2)过点作,垂足为,根据即可求解.
【详解】解:(1)①先作的垂直平分线:分别以B,C为圆心,大于的长为半径画弧,连接两个交点即为直线l,分别交、于、;
②再作的角平分线:以点B为圆心,任意长为半径作圆弧,与的两条边分别有一个交点,再以这两个交点为圆心,相同长度为半径作弧,连接这两条弧的交点与点B,即为的角平分线,这条角平分线与线段MN的交点即为;
③以为圆心,为半径画圆,圆即为所求;
(2)过点作,垂足为,设
∵,,∴,∴
根据面积法,∴
∴,解得,
故答案为:.
【点睛】本题考查了尺规作图,切线的性质等内容,解题的关键是掌握线段垂直平分线、角平分线的尺规作图.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
