2.6正多边形与圆暑假预习练(含解析) 苏科版数学九年级上册
文档属性
| 名称 | 2.6正多边形与圆暑假预习练(含解析) 苏科版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-09 11:31:04 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2.6正多边形与圆
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,四边形内接于⊙O ,,那么等于( )
A.110° B.135° C.55° D.125°
2.顺次连接正六边形的三个不相邻的顶点,得到如图的图形,下列说法错误的是( )
A.△ACE是等边三角形
B.既是轴对称图形也是中心对称图形
C.连接AD,则AD分别平分∠EAC与∠EDC
D.图中一共能画出3条对称轴
3.如图,在平面直角坐标系中,边长为2的正六边形的中心与原点重合,轴,交轴于点.将绕点顺时针旋转,每次旋转,则第2023次旋转结束时,点的坐标为( )
A. B. C. D.
4.正多边形的中心角与该正多边形一个内角的关系是( )
A.互余 B.互补 C.互余或互补 D.不能确定
5.如图,点是正六边形的中心,则的度数是( )
A. B. C. D.
6.如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环共需要的正五边形个数是( )
A.8 B.9 C.10 D.11
7.如图,点O为正六边形的中心,P、Q分别从点同时出发,沿正六边形按图示方向运动,点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,则第2021次相遇地点的坐标为( )
A. B.(1,0) C. D.(﹣1,0)
8.如图所示,直线AB, AD与⊙O分别相切于点B, D, C为⊙O上一点,且∠BCD=140°,则∠A的度数是( )
A.70° B.105° C.100° D.110°
9.半径为2的圆的一个内接正多边形的内角为,则这个内接正多边形的边长为( )
A.1 B.2 C. D.
10.已知圆内接正三角形的面积为,则该圆的内接正六边形的边心距是()
A. B. C. D.
11.如图,正五边形的边长为2,以为圆心,以为半径作弧,则阴影部分的面积为( )
A. B. C. D.
12.如图,半径为1的⊙O与正六边形ABCDEF相切于点A、D,则弧AD的长为( )
A. B. C. D.
二、填空题
13.如图,点A、B、C在⊙O上,∠AOC=60 ,则∠ABC= .
14.如图是四个全等的正八边形和一个正方形拼成的图案,已知正方形的面积为4,则一个正八边形的面积为 .
15.如图,若的半径为1,则的内接正八边形的面积为 .
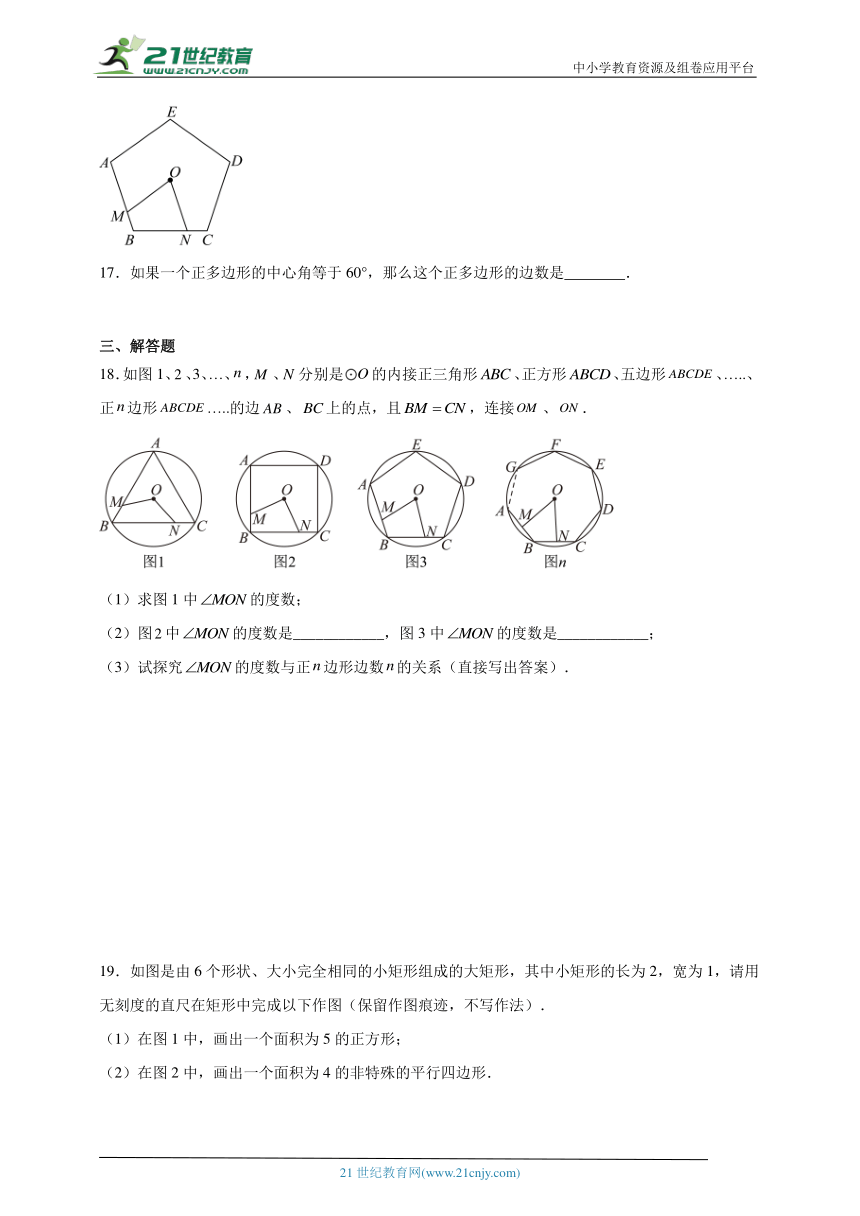
16.如图,点M、N分别是正五边形ABCDE的两边AB、BC上的点.且AM=BN,点O是正五边形的中心,则∠MON的度数是 度.
17.如果一个正多边形的中心角等于60°,那么这个正多边形的边数是 .
三、解答题
18.如图1、、3、…、,、分别是的内接正三角形、正方形、五边形、…..、正边形…..的边、上的点,且,连接、.
(1)求图1中的度数;
(2)图中的度数是____________,图3中的度数是____________;
(3)试探究的度数与正边形边数的关系(直接写出答案).
19.如图是由6个形状、大小完全相同的小矩形组成的大矩形,其中小矩形的长为2,宽为1,请用无刻度的直尺在矩形中完成以下作图(保留作图痕迹,不写作法).
(1)在图1中,画出一个面积为5的正方形;
(2)在图2中,画出一个面积为4的非特殊的平行四边形.
20.(1)如图①,把等边三角形的各边三等分,分别以居中那条线段为一边向外作等边三角形,并去掉居中的那条线段,得到一个六角星,则这个六角星的边数是_______.
(2)如图②,在5×5的网格中有一个正方形,把正方形的各边三等分,分别以居中那条线段为一边向外作正方形,并去掉居中的那条线段.请你把得到的图形画在图③中,并写出这个图形的边数.
(3)现有一个正五边形,把正五边形的各边三等分,分别以居中那条线段为一边向外作正五边形,并去掉居中的那条线段,得到的图形的边数是多少?
21.如图所示,四边形ABCD内接于⊙O,延长AD,BC相交于点M,延长AB,DC相交于点N,∠M=40°,∠N=20°,求∠A的度数.
22.如图所示中,,,分别在边和上,且,,垂足分别为,,求的长.
23.如图,⊙O的半径为,其内接正六边形,点同时分别从两点出发,以的速度沿向终点运动,连接.设运动时间为.
(1)求证:四边形为平行四边形;
(2)填空:
①当________时,四边形为菱形;
②当_________时,四边形为矩形.
24.如图,要拧开一个边长的六角形螺帽,扳手张开的开口b至少要多少?
《2.6正多边形与圆》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B C B B C C C B B
题号 11 12
答案 D C
1.D
【分析】根据已知条件可知,,根据圆内接四边形的对角互补可知,由此即可解答.
【详解】解:.
∵四边形内接于⊙O
.
,
故选:D.
【点睛】本题主要考查了圆心角、圆周角、弦的关系以及圆的内接四边形的性质,掌握相关知识点,得到、是关键.
2.B
【详解】试题解析:A.∵多边形ABCDEF是正六边形,
∴△ACE是等边三角形,故本选项正确;
B.∵△ACE是等边三角形,∴是轴对称图形,不是中心对称图形,故本选项错误;
C.∵△ACE是等边三角形,∴连接AD,则AD分别平分∠EAC与∠EDC,故本选项正确;
D.∵△ACE是等边三角形,∴图中一共能画3条对称轴,故本选项正确.
故选B.
3.C
【分析】本题考查了正多边形的性质、坐标与图形的变化—旋转规律性问题,首先确定点的坐标,得出每次一个循环,计算出,由此即可得出答案,得出规律是解此题的关键.
【详解】解:正六边形的边长为,中心与原点重合,轴,交轴于点,
,,,
,
∴点的坐标为,
第次旋转结束时,点旋转到第四象限,坐标为,
第次旋转结束时,点旋转到第三象限,坐标为,
第次旋转结束时,点旋转到第二象限,坐标为,
第次旋转结束时,点的坐标为,
每次一个循环,
,
第2023次旋转结束时,点的坐标为,
故选:C.
4.B
【详解】设正多边形的边数为n,则正多边形的中心角为,正多边形的一个外角等于,所以正多边形的中心角等于正多边形的一个外角,而正多边形的一个外角与该正多边形相邻的一个内角的互补,所以正多边形的中心角与该正多边形一个内角互补.
故选B.
5.B
【分析】本题考查正多边形和圆,正确记忆相关知识点是解题关键.根据正六边形的性质可得,,从而求出.
【详解】解:连接,
点为正六边形的中心,
,
故选:B
6.C
【分析】本题考查了正五边形与圆的有关运算,解题的关键是正确的构造圆心角.延长正五边形的相邻两边交于圆心,求得该圆心角的度数后,用除以该圆心角的度数即可得到正五边形的个数,从而得到答案.
【详解】解:如图,圆心角为,
∵五边形的内角和为:,
∴五边形的每一个内角为:,
,
,
∴要完成这一圆环共需10个全等的五边形,
故选:C.
7.C
【分析】连接,证是等边三角形,得,过B作于点G,则,,得,再由题意得P,Q第一次相遇地点的坐标在点,第二次相遇地点在点,第三次相遇地点在点,如此循环下去,即可求出第2021次相遇地点的坐标.
【详解】解:连接OB,如图所示,
∵,O为正六边形的中心,
∴,
∵,
∴是等边三角形,
∴,
过B作于点G,则,,
∴,
∴,,
∵正六边形的边长=1,
∴正六边形的周长=6,
∵点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,
∴第1次相遇需要的时间为:(秒),
此时点P的路程为,点的Q路程为,
此时P,Q相遇地点的坐标在点,
以此类推:第二次相遇地点在点,
第三次相遇地点在点,…如此下去,
∵,
∴第2021次相遇地点在点E,E的坐标为,
故选:C.
【点睛】本题考查了正多边形和圆、规律型﹣点的坐标、等边三角形的判定与性质等知识;熟练掌握正六边形的性质,解决本题的关键是找出规律.
8.C
【详解】试题分析:过点B作直径BE,连接OD、DE.根据圆内接四边形性质:对角互补,可求∠E=180°﹣∠BCD =180°﹣140°=40°;根据圆周角定理求∠BOD=80°;根据切线的性质可知∠OBA=∠ODA=90°,根据四边形内角和定理可求得∠A=360°﹣90°﹣90°﹣80°=100°.
故选C.
考点:切线的性质;圆周角定理;圆内接四边形的性质
9.B
【分析】本题考查正多边形和圆,掌握正六边形的性质是正确解答的前提.
根据正六边形的性质,正三角形的性质进行计算即可.
【详解】解:如图,
∵半径为2的圆的一个内接正多边形的内角为,
∴,
∴,
∴的内接正多边形是六边形,
,
,
∴是正三角形,
,
∴正六边形的边长为2,
故选:B.
10.B
【分析】根据题意可以求得半径,进而解答即可.
【详解】因为圆内接正三角形的面积为,
所以圆的半径为,
所以该圆的内接正六边形的边心距×sin60°=×=1,
故选B.
【点睛】本题考查正多边形和圆,解答本题的关键是明确题意,求出相应的图形的边心距.
11.D
【分析】本题考查了多边形的内角和问题、求扇形面积,由题意得出,,再由扇形面积公式计算即可得出答案.
【详解】解:正五边形的边长为2,
,,
阴影部分的面积为,
故选:D.
12.C
【详解】试题解析:连接OA,OD,
∵⊙O与正六边形ABCDEF相切于点A、D,
∴∠OAF=∠ODE=90°,
∵∠E=∠F=120°,
∴∠AOD=540°-90°-90°-120°-120°=120°,
∴的长为,
故选C.
13.150
【详解】如图,在优弧 ADC 上取点D,连接AD,CD,
∵∠AOC=60°,∴∠ADC=∠AOC=30°.
∵∠ABC+∠ADC=180°,∴∠ABC=180°-∠ADC=180°-30°=150°.
14.
【分析】根据正方形的性质得到AB=2,根据由正八边形的特点求出∠AOB的度数,过点B作BD⊥OA于点D,根据勾股定理求出BD的长,由三角形的面积公式求出△AOB的面积,进而可得出结论.
【详解】解:设正八边形的中心为O,
连接OA,OB,如图所示,
∵正方形的面积为4,
∴AB=2,
∵AB是正八边形的一条边,
∴∠AOB==45°.
过点B作BD⊥OA于点D,设BD=x,则OD=x,OB=OA=x,
∴AD=x-x,
在Rt△ADB中,BD2+AD2=AB2,
即x2+(x-x)2=22,
解得x2=2+,
∴S△AOB=OA BD=×x2=+1,
∴S正八边形=8S△AOB=8×(+1)=8+8,
故答案为:8+8.
【点睛】本题考查的是正多边形和圆,正方形的性质,三角形面积的计算,根据题意画出图形,利用数形结合求解是解答此题的关键.
15.
【分析】利用勾股定理求出正方形的边长,根据即可.
【详解】
解:连接,,,
∵四边形是圆内接正四边形,,是圆的直径,,
,
,
,
,
,
故答案为:.
【点睛】本题考查了圆内接正多边形,利用圆内接正多边形的性质求出正方形的边长是解题的关键.
16.72
【详解】【分析】连接OA、OB、OC,根据正多边形的中心角的计算公式求出∠AOB,证明△AOM≌△BON,根据全等三角形的性质得到∠BON=∠AOM,得到答案.
【详解】如图,连接OA、OB、OC,
∠AOB==72°,
∵∠AOB=∠BOC,OA=OB,OB=OC,
∴∠OAB=∠OBC,
在△AOM和△BON中,
,
∴△AOM≌△BON,
∴∠BON=∠AOM,
∴∠MON=∠AOB=72°,
故答案为72.
【点睛】本题考查的是正多边形和圆的有关计算,掌握正多边形与圆的关系、全等三角形的判定定理和性质定理是解题的关键.
17.6
【分析】根据正n边形的中心角的度数为进行计算即可得到答案.
【详解】根据正n边形的中心角的度数为,
则,故这个正多边形的边数为6,
故答案为:6.
【点睛】本题考查的是正多边形内角和中心角的知识,掌握中心角的计算公式是解题的关键.
18.(1);(2),;(3)
【详解】试题分析:连接BO,CO那么,有:BM=CM, ∠OBM=∠OCN,BO=CO,利用SAS证明△OBM≌△OCN,同理可得,图1中的∠MON=∠BOC=120°,图2中心角等于360°÷4=90°,图3的中心角等于360°÷5=72°,所以,(1)120°,(2)90° 72°,(3)正n边形时, ∠MON=∠BOC=360°÷n, ∠MON是一定值,取特殊位置进行分析,对三个图取B与M重合,N与C重合,即可求出∠MON的值.
试题解析:(1)解法一:连接OB,OC,
∵正△ABC内接于⊙O,
∴∠OBM=∠OCN=30°,∠BOC=120°.
又∵BM=CN,OB=OC,
∴△OBM≌△OCN,
∴∠BOM=∠OCN,
∴∠MON=∠BOC=120°.
解法二:连接OA,OB,
∵正△ABC内接于⊙O,
∴AB=AC,∠OAM=∠OBN=30°,∠AOB=120°,
又∵BM=CN,
∴AM=BN,
又∵OA=OB,
∴△AOM≌△BON,
∴∠AOM=∠BON,
∴∠AON=∠AOB=120°.
(2)90°, 72°.
(3)∠MON=.
19.见解析
【分析】(1)直接利用正方形的判定方法得出答案;
(2)直接利用平行四边形的判定方法得出答案.
【详解】(1)如图正方形ABCD;
(2)如图平行四边形EFGH
.
【点睛】此题考查应用设计与作图,正确掌握平行四边形以及正方形的判定方法是解题关键.
20.(1)12;(2)图详见解析,这个图形的边数是20; (3)图详见解析,得到的图形的边数是30.
【分析】根据题目要求画图,再在图中得出题目要求的问题.
【详解】解:(1)把等边三角形的各边三等分,分别以居中那条线段为一边向外作等边三角形,并去掉居中的那条线段,得到一个六角星(如图所示),
故此多边形的边数是:12.
(2)这个图形的边数是20.
(3)得到的图形的边数是30.
【点睛】本题考查学生读题和按题意画图的能力,掌握根据题意画图的能力是解决此题的关键.
21.∠A=60°.
【分析】根据圆内接四边形的性质可得∠1=∠2=∠A,由圆周角定理可得答案.
【详解】∵四边形ABCD内接于⊙O
∴∠1=∠2=∠A.
∵∠ADC+∠ABC=180°,∠ADC=∠M+∠2,∠ABC=∠1+∠N,
∴∠M+∠1+∠2+∠N=180°
∵∠M=40°,∠N=20°,∠1=∠2=∠A
∴∠A=60°.
【点睛】本题考查圆周角定理和圆内接四边形的性质,解题的关键是熟练掌握圆周角定理和圆内接四边形的性质.
22.
【分析】本题关键要建立未知线段和已知线段的关系,由,,,共圆,和为直径,于是在中便可以建立和的关系,求出的长即求出的长.
【详解】连结,,∵,
∴∴,
∴由圆的定义知点,,,在以为圆心,为半径的圆上,作出辅助圆,延长交圆于,连结,
∴
在中,,∴ ∴
【点睛】双直角三角形是典型的共圆图,解题中注意灵活应用.
23.(1)见解析;(2)①2;②0或4
【分析】(1)根据题意可得,,然后证明,由此可得、,进而可证结论.
(2)①根据菱形的性质,,时,四边形是菱形,由此可知t=2;
②根据矩形的性质,当有三个角是直角时,四边形是矩形,由此可知t=4或0.
【详解】(1)∵正六边形内接于的半径为4,
,
∵点同时分别从两点出发,以的速度沿向终点运动,.
在和中,
同理可证.
∴四边形是平行四边形.
(2)①2;②0或4 ,
①由对称性可知,当,时,四边形是菱形,此时.
②当时,点在点处, ,,此时四边形是矩形.
当时,点在点处,同理可得,此时四边形是矩形.综上所述,当或时,四边形是矩形.
【点睛】本题主要考查平行四边形、菱形、矩形的性质与判定,涉及动点问题,掌握各图形的性质及判定方法是解题关键.
24.扳手张开的开口b至少要12mm.
【分析】由题意可得:六边形为正六边形,可得六边形的六条边相等,每个内角为过点A作AG⊥BF,垂足为点G,再利用含的直角三角形的性质求解 再利用勾股定理求解 结合等腰三角形的性质可得答案.
【详解】解:如图所示,由题意得:六边形为正六边形,
六边形的六条边相等,每个内角为
过点A作AG⊥BF,垂足为点G,
因为∠BAF=120°,
所以∠BAG=60°,
所以∠ABG=30°,
在Rt△ABG中,AB=12mm,∠AGB=90°,∠ABG=30°,
所以AG=AB=×12=6(mm),
由勾股定理得BG===6(mm),
即b=BF=2BG=2×6=12 (mm).
答:扳手张开的开口b至少要12mm.
【点睛】本题考查的是正多边形与圆,含的直角三角形的性质,勾股定理的应用,等腰三角形的性质,熟练应用以上知识解题是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.6正多边形与圆
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,四边形内接于⊙O ,,那么等于( )
A.110° B.135° C.55° D.125°
2.顺次连接正六边形的三个不相邻的顶点,得到如图的图形,下列说法错误的是( )
A.△ACE是等边三角形
B.既是轴对称图形也是中心对称图形
C.连接AD,则AD分别平分∠EAC与∠EDC
D.图中一共能画出3条对称轴
3.如图,在平面直角坐标系中,边长为2的正六边形的中心与原点重合,轴,交轴于点.将绕点顺时针旋转,每次旋转,则第2023次旋转结束时,点的坐标为( )
A. B. C. D.
4.正多边形的中心角与该正多边形一个内角的关系是( )
A.互余 B.互补 C.互余或互补 D.不能确定
5.如图,点是正六边形的中心,则的度数是( )
A. B. C. D.
6.如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环共需要的正五边形个数是( )
A.8 B.9 C.10 D.11
7.如图,点O为正六边形的中心,P、Q分别从点同时出发,沿正六边形按图示方向运动,点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,则第2021次相遇地点的坐标为( )
A. B.(1,0) C. D.(﹣1,0)
8.如图所示,直线AB, AD与⊙O分别相切于点B, D, C为⊙O上一点,且∠BCD=140°,则∠A的度数是( )
A.70° B.105° C.100° D.110°
9.半径为2的圆的一个内接正多边形的内角为,则这个内接正多边形的边长为( )
A.1 B.2 C. D.
10.已知圆内接正三角形的面积为,则该圆的内接正六边形的边心距是()
A. B. C. D.
11.如图,正五边形的边长为2,以为圆心,以为半径作弧,则阴影部分的面积为( )
A. B. C. D.
12.如图,半径为1的⊙O与正六边形ABCDEF相切于点A、D,则弧AD的长为( )
A. B. C. D.
二、填空题
13.如图,点A、B、C在⊙O上,∠AOC=60 ,则∠ABC= .
14.如图是四个全等的正八边形和一个正方形拼成的图案,已知正方形的面积为4,则一个正八边形的面积为 .
15.如图,若的半径为1,则的内接正八边形的面积为 .
16.如图,点M、N分别是正五边形ABCDE的两边AB、BC上的点.且AM=BN,点O是正五边形的中心,则∠MON的度数是 度.
17.如果一个正多边形的中心角等于60°,那么这个正多边形的边数是 .
三、解答题
18.如图1、、3、…、,、分别是的内接正三角形、正方形、五边形、…..、正边形…..的边、上的点,且,连接、.
(1)求图1中的度数;
(2)图中的度数是____________,图3中的度数是____________;
(3)试探究的度数与正边形边数的关系(直接写出答案).
19.如图是由6个形状、大小完全相同的小矩形组成的大矩形,其中小矩形的长为2,宽为1,请用无刻度的直尺在矩形中完成以下作图(保留作图痕迹,不写作法).
(1)在图1中,画出一个面积为5的正方形;
(2)在图2中,画出一个面积为4的非特殊的平行四边形.
20.(1)如图①,把等边三角形的各边三等分,分别以居中那条线段为一边向外作等边三角形,并去掉居中的那条线段,得到一个六角星,则这个六角星的边数是_______.
(2)如图②,在5×5的网格中有一个正方形,把正方形的各边三等分,分别以居中那条线段为一边向外作正方形,并去掉居中的那条线段.请你把得到的图形画在图③中,并写出这个图形的边数.
(3)现有一个正五边形,把正五边形的各边三等分,分别以居中那条线段为一边向外作正五边形,并去掉居中的那条线段,得到的图形的边数是多少?
21.如图所示,四边形ABCD内接于⊙O,延长AD,BC相交于点M,延长AB,DC相交于点N,∠M=40°,∠N=20°,求∠A的度数.
22.如图所示中,,,分别在边和上,且,,垂足分别为,,求的长.
23.如图,⊙O的半径为,其内接正六边形,点同时分别从两点出发,以的速度沿向终点运动,连接.设运动时间为.
(1)求证:四边形为平行四边形;
(2)填空:
①当________时,四边形为菱形;
②当_________时,四边形为矩形.
24.如图,要拧开一个边长的六角形螺帽,扳手张开的开口b至少要多少?
《2.6正多边形与圆》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B C B B C C C B B
题号 11 12
答案 D C
1.D
【分析】根据已知条件可知,,根据圆内接四边形的对角互补可知,由此即可解答.
【详解】解:.
∵四边形内接于⊙O
.
,
故选:D.
【点睛】本题主要考查了圆心角、圆周角、弦的关系以及圆的内接四边形的性质,掌握相关知识点,得到、是关键.
2.B
【详解】试题解析:A.∵多边形ABCDEF是正六边形,
∴△ACE是等边三角形,故本选项正确;
B.∵△ACE是等边三角形,∴是轴对称图形,不是中心对称图形,故本选项错误;
C.∵△ACE是等边三角形,∴连接AD,则AD分别平分∠EAC与∠EDC,故本选项正确;
D.∵△ACE是等边三角形,∴图中一共能画3条对称轴,故本选项正确.
故选B.
3.C
【分析】本题考查了正多边形的性质、坐标与图形的变化—旋转规律性问题,首先确定点的坐标,得出每次一个循环,计算出,由此即可得出答案,得出规律是解此题的关键.
【详解】解:正六边形的边长为,中心与原点重合,轴,交轴于点,
,,,
,
∴点的坐标为,
第次旋转结束时,点旋转到第四象限,坐标为,
第次旋转结束时,点旋转到第三象限,坐标为,
第次旋转结束时,点旋转到第二象限,坐标为,
第次旋转结束时,点的坐标为,
每次一个循环,
,
第2023次旋转结束时,点的坐标为,
故选:C.
4.B
【详解】设正多边形的边数为n,则正多边形的中心角为,正多边形的一个外角等于,所以正多边形的中心角等于正多边形的一个外角,而正多边形的一个外角与该正多边形相邻的一个内角的互补,所以正多边形的中心角与该正多边形一个内角互补.
故选B.
5.B
【分析】本题考查正多边形和圆,正确记忆相关知识点是解题关键.根据正六边形的性质可得,,从而求出.
【详解】解:连接,
点为正六边形的中心,
,
故选:B
6.C
【分析】本题考查了正五边形与圆的有关运算,解题的关键是正确的构造圆心角.延长正五边形的相邻两边交于圆心,求得该圆心角的度数后,用除以该圆心角的度数即可得到正五边形的个数,从而得到答案.
【详解】解:如图,圆心角为,
∵五边形的内角和为:,
∴五边形的每一个内角为:,
,
,
∴要完成这一圆环共需10个全等的五边形,
故选:C.
7.C
【分析】连接,证是等边三角形,得,过B作于点G,则,,得,再由题意得P,Q第一次相遇地点的坐标在点,第二次相遇地点在点,第三次相遇地点在点,如此循环下去,即可求出第2021次相遇地点的坐标.
【详解】解:连接OB,如图所示,
∵,O为正六边形的中心,
∴,
∵,
∴是等边三角形,
∴,
过B作于点G,则,,
∴,
∴,,
∵正六边形的边长=1,
∴正六边形的周长=6,
∵点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,
∴第1次相遇需要的时间为:(秒),
此时点P的路程为,点的Q路程为,
此时P,Q相遇地点的坐标在点,
以此类推:第二次相遇地点在点,
第三次相遇地点在点,…如此下去,
∵,
∴第2021次相遇地点在点E,E的坐标为,
故选:C.
【点睛】本题考查了正多边形和圆、规律型﹣点的坐标、等边三角形的判定与性质等知识;熟练掌握正六边形的性质,解决本题的关键是找出规律.
8.C
【详解】试题分析:过点B作直径BE,连接OD、DE.根据圆内接四边形性质:对角互补,可求∠E=180°﹣∠BCD =180°﹣140°=40°;根据圆周角定理求∠BOD=80°;根据切线的性质可知∠OBA=∠ODA=90°,根据四边形内角和定理可求得∠A=360°﹣90°﹣90°﹣80°=100°.
故选C.
考点:切线的性质;圆周角定理;圆内接四边形的性质
9.B
【分析】本题考查正多边形和圆,掌握正六边形的性质是正确解答的前提.
根据正六边形的性质,正三角形的性质进行计算即可.
【详解】解:如图,
∵半径为2的圆的一个内接正多边形的内角为,
∴,
∴,
∴的内接正多边形是六边形,
,
,
∴是正三角形,
,
∴正六边形的边长为2,
故选:B.
10.B
【分析】根据题意可以求得半径,进而解答即可.
【详解】因为圆内接正三角形的面积为,
所以圆的半径为,
所以该圆的内接正六边形的边心距×sin60°=×=1,
故选B.
【点睛】本题考查正多边形和圆,解答本题的关键是明确题意,求出相应的图形的边心距.
11.D
【分析】本题考查了多边形的内角和问题、求扇形面积,由题意得出,,再由扇形面积公式计算即可得出答案.
【详解】解:正五边形的边长为2,
,,
阴影部分的面积为,
故选:D.
12.C
【详解】试题解析:连接OA,OD,
∵⊙O与正六边形ABCDEF相切于点A、D,
∴∠OAF=∠ODE=90°,
∵∠E=∠F=120°,
∴∠AOD=540°-90°-90°-120°-120°=120°,
∴的长为,
故选C.
13.150
【详解】如图,在优弧 ADC 上取点D,连接AD,CD,
∵∠AOC=60°,∴∠ADC=∠AOC=30°.
∵∠ABC+∠ADC=180°,∴∠ABC=180°-∠ADC=180°-30°=150°.
14.
【分析】根据正方形的性质得到AB=2,根据由正八边形的特点求出∠AOB的度数,过点B作BD⊥OA于点D,根据勾股定理求出BD的长,由三角形的面积公式求出△AOB的面积,进而可得出结论.
【详解】解:设正八边形的中心为O,
连接OA,OB,如图所示,
∵正方形的面积为4,
∴AB=2,
∵AB是正八边形的一条边,
∴∠AOB==45°.
过点B作BD⊥OA于点D,设BD=x,则OD=x,OB=OA=x,
∴AD=x-x,
在Rt△ADB中,BD2+AD2=AB2,
即x2+(x-x)2=22,
解得x2=2+,
∴S△AOB=OA BD=×x2=+1,
∴S正八边形=8S△AOB=8×(+1)=8+8,
故答案为:8+8.
【点睛】本题考查的是正多边形和圆,正方形的性质,三角形面积的计算,根据题意画出图形,利用数形结合求解是解答此题的关键.
15.
【分析】利用勾股定理求出正方形的边长,根据即可.
【详解】
解:连接,,,
∵四边形是圆内接正四边形,,是圆的直径,,
,
,
,
,
,
故答案为:.
【点睛】本题考查了圆内接正多边形,利用圆内接正多边形的性质求出正方形的边长是解题的关键.
16.72
【详解】【分析】连接OA、OB、OC,根据正多边形的中心角的计算公式求出∠AOB,证明△AOM≌△BON,根据全等三角形的性质得到∠BON=∠AOM,得到答案.
【详解】如图,连接OA、OB、OC,
∠AOB==72°,
∵∠AOB=∠BOC,OA=OB,OB=OC,
∴∠OAB=∠OBC,
在△AOM和△BON中,
,
∴△AOM≌△BON,
∴∠BON=∠AOM,
∴∠MON=∠AOB=72°,
故答案为72.
【点睛】本题考查的是正多边形和圆的有关计算,掌握正多边形与圆的关系、全等三角形的判定定理和性质定理是解题的关键.
17.6
【分析】根据正n边形的中心角的度数为进行计算即可得到答案.
【详解】根据正n边形的中心角的度数为,
则,故这个正多边形的边数为6,
故答案为:6.
【点睛】本题考查的是正多边形内角和中心角的知识,掌握中心角的计算公式是解题的关键.
18.(1);(2),;(3)
【详解】试题分析:连接BO,CO那么,有:BM=CM, ∠OBM=∠OCN,BO=CO,利用SAS证明△OBM≌△OCN,同理可得,图1中的∠MON=∠BOC=120°,图2中心角等于360°÷4=90°,图3的中心角等于360°÷5=72°,所以,(1)120°,(2)90° 72°,(3)正n边形时, ∠MON=∠BOC=360°÷n, ∠MON是一定值,取特殊位置进行分析,对三个图取B与M重合,N与C重合,即可求出∠MON的值.
试题解析:(1)解法一:连接OB,OC,
∵正△ABC内接于⊙O,
∴∠OBM=∠OCN=30°,∠BOC=120°.
又∵BM=CN,OB=OC,
∴△OBM≌△OCN,
∴∠BOM=∠OCN,
∴∠MON=∠BOC=120°.
解法二:连接OA,OB,
∵正△ABC内接于⊙O,
∴AB=AC,∠OAM=∠OBN=30°,∠AOB=120°,
又∵BM=CN,
∴AM=BN,
又∵OA=OB,
∴△AOM≌△BON,
∴∠AOM=∠BON,
∴∠AON=∠AOB=120°.
(2)90°, 72°.
(3)∠MON=.
19.见解析
【分析】(1)直接利用正方形的判定方法得出答案;
(2)直接利用平行四边形的判定方法得出答案.
【详解】(1)如图正方形ABCD;
(2)如图平行四边形EFGH
.
【点睛】此题考查应用设计与作图,正确掌握平行四边形以及正方形的判定方法是解题关键.
20.(1)12;(2)图详见解析,这个图形的边数是20; (3)图详见解析,得到的图形的边数是30.
【分析】根据题目要求画图,再在图中得出题目要求的问题.
【详解】解:(1)把等边三角形的各边三等分,分别以居中那条线段为一边向外作等边三角形,并去掉居中的那条线段,得到一个六角星(如图所示),
故此多边形的边数是:12.
(2)这个图形的边数是20.
(3)得到的图形的边数是30.
【点睛】本题考查学生读题和按题意画图的能力,掌握根据题意画图的能力是解决此题的关键.
21.∠A=60°.
【分析】根据圆内接四边形的性质可得∠1=∠2=∠A,由圆周角定理可得答案.
【详解】∵四边形ABCD内接于⊙O
∴∠1=∠2=∠A.
∵∠ADC+∠ABC=180°,∠ADC=∠M+∠2,∠ABC=∠1+∠N,
∴∠M+∠1+∠2+∠N=180°
∵∠M=40°,∠N=20°,∠1=∠2=∠A
∴∠A=60°.
【点睛】本题考查圆周角定理和圆内接四边形的性质,解题的关键是熟练掌握圆周角定理和圆内接四边形的性质.
22.
【分析】本题关键要建立未知线段和已知线段的关系,由,,,共圆,和为直径,于是在中便可以建立和的关系,求出的长即求出的长.
【详解】连结,,∵,
∴∴,
∴由圆的定义知点,,,在以为圆心,为半径的圆上,作出辅助圆,延长交圆于,连结,
∴
在中,,∴ ∴
【点睛】双直角三角形是典型的共圆图,解题中注意灵活应用.
23.(1)见解析;(2)①2;②0或4
【分析】(1)根据题意可得,,然后证明,由此可得、,进而可证结论.
(2)①根据菱形的性质,,时,四边形是菱形,由此可知t=2;
②根据矩形的性质,当有三个角是直角时,四边形是矩形,由此可知t=4或0.
【详解】(1)∵正六边形内接于的半径为4,
,
∵点同时分别从两点出发,以的速度沿向终点运动,.
在和中,
同理可证.
∴四边形是平行四边形.
(2)①2;②0或4 ,
①由对称性可知,当,时,四边形是菱形,此时.
②当时,点在点处, ,,此时四边形是矩形.
当时,点在点处,同理可得,此时四边形是矩形.综上所述,当或时,四边形是矩形.
【点睛】本题主要考查平行四边形、菱形、矩形的性质与判定,涉及动点问题,掌握各图形的性质及判定方法是解题关键.
24.扳手张开的开口b至少要12mm.
【分析】由题意可得:六边形为正六边形,可得六边形的六条边相等,每个内角为过点A作AG⊥BF,垂足为点G,再利用含的直角三角形的性质求解 再利用勾股定理求解 结合等腰三角形的性质可得答案.
【详解】解:如图所示,由题意得:六边形为正六边形,
六边形的六条边相等,每个内角为
过点A作AG⊥BF,垂足为点G,
因为∠BAF=120°,
所以∠BAG=60°,
所以∠ABG=30°,
在Rt△ABG中,AB=12mm,∠AGB=90°,∠ABG=30°,
所以AG=AB=×12=6(mm),
由勾股定理得BG===6(mm),
即b=BF=2BG=2×6=12 (mm).
答:扳手张开的开口b至少要12mm.
【点睛】本题考查的是正多边形与圆,含的直角三角形的性质,勾股定理的应用,等腰三角形的性质,熟练应用以上知识解题是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
