2.5一元一次方程暑假预习练(含解析) 北京版数学七年级上册
文档属性
| 名称 | 2.5一元一次方程暑假预习练(含解析) 北京版数学七年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 599.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-09 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2.5一元一次方程
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.当k取何值时,与的解相同?( )
A. B. C.4 D.3
2.方程的解是( )
A. B. C. D.
3.方程的解是( ).
A. B. C. D.
4.若关于x的方程是一元一次方程,则a,b应满足的条件是( )
A. B.
C. D.
5.已知与是同类项,则的值是( )
A.12 B.13 C.16 D.17
6.下列解方程变形正确的是( )
A.由得 B.由得
C.由得 D.由得
7.方程x+1=5的解是( )
A.x=﹣6 B.x=6 C.x=4 D.x=﹣4
8.下列方程中,解为的方程是( ).
A. B. C. D.
9.若对于任意实数a,b,c,d,定义,按照定义,若,则x的值为( )
A.1 B. C. D.5
10.对于非零的两个有理数a,b,规定,若,则x的值为( )
A. B. C. D.
11.解方程,去分母正确的是( )
A. B.
C. D.
12.如果是关于的方程的解,则的值是 ( )
A. B.2 C. D.1
二、填空题
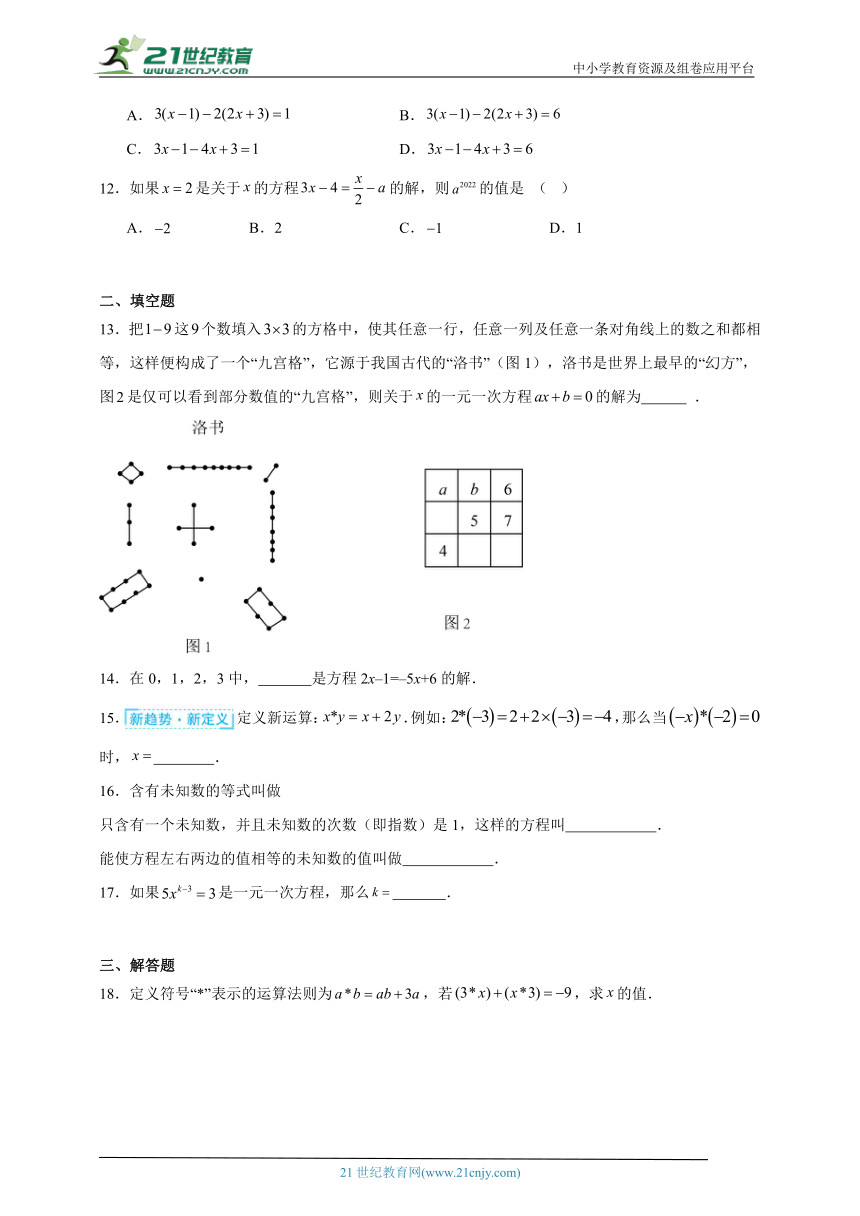
13.把这个数填入的方格中,使其任意一行,任意一列及任意一条对角线上的数之和都相等,这样便构成了一个“九宫格”,它源于我国古代的“洛书”(图1),洛书是世界上最早的“幻方”,图是仅可以看到部分数值的“九宫格”,则关于的一元一次方程的解为 .
14.在0,1,2,3中, 是方程2x–1=–5x+6的解.
15.定义新运算:.例如:,那么当时, .
16.含有未知数的等式叫做
只含有一个未知数,并且未知数的次数(即指数)是1,这样的方程叫 .
能使方程左右两边的值相等的未知数的值叫做 .
17.如果是一元一次方程,那么 .
三、解答题
18.定义符号“*”表示的运算法则为,若,求的值.
19.解方程
(1)
(2)
20.解下列方程:
(1);
(2).
21.解下列方程:
(1);
(2).
22.解方程:.
23.解下列方程:
(1)
(2)
(3)
(4)
24.解方程:
(1)3-(4x-3)=7
(2)2x-(x+10)=5x+2(x-1)
《2.5一元一次方程》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D A C C B C C C C C
题号 11 12
答案 B D
1.D
【分析】此题主要考查了同解方程,首先根据解一元一次方程的方法,求出的解是多少;然后把求出的x的值代入,求出k的值是多少即可.
【详解】解:解得,
把代入得,
解得.
故选:D.
2.A
【分析】本题考查解一元一次方程,直接利用系数化为解题即可.
【详解】解:两边同时除以得到,
故选A.
3.C
【解析】略
4.C
【分析】只含有一个未知数(元),且未知数的指数为1的方程叫做一元一次方程,它的一般形式是(a、b是常数,且),根据一元一次方程的定义求出答案.
【详解】解:根据题题意得:,
解得:.
故选:C.
【点睛】本题考查了一元一次方程的一般形式,只含有一个未知数(元),且未知数的指数为1,一次项系数不是0,这是此类题目考查的重点.
5.B
【分析】本题考查同类项的概念、解一元一次方程等,同类项是指所含的字母相同,并且相同字母的指数也分别相同的两个单项式.解题的关键是理解同类项的概念求出的值.
根据同类项的概念列出关于的一元一次方程,解得的值后,代入式子即可得出结论.
【详解】解:与是同类项,
,,
解得:,,
故选:B.
6.C
【分析】根据解一元一次方程的步骤:去分母,去括号,移项,合并同类项,系数化为1逐个检验即可求解.
【详解】解:选项A:方程两边都乘2,即可得到,故本选项错误;
选项B:方程两边都除以3,即可得到,故本选项错误;
选项C:移项得,合并同类项得,系数化为1得,故本选项正确;
选项D.移项得,故本选项错误,
故选:C.
【点睛】本题考查了解一元一次方程的步骤及解法,属于基础题,移项时要记得变号,同时计算过程要细心.
7.C
【分析】方程移项合并,即可求出解.
【详解】解:方程x+1=5,
移项得:x=5-1,
合并得:x=4.
故选:C.
【点睛】此题考查了解一元一次方程,熟练掌握一元一次方程的解法是解本题的关键.
8.C
【分析】本题考查了一元一次方程的解,依次解方程即可.
【详解】A、,解得:,不符合题意,选项错误;
B、,解得:,不符合题意,选项错误;
C、,解得:,符合题意,选项正确;
D、,解得:,不符合题意,选项错误;
故选:C.
9.C
【分析】根据题目所给的新定义得到关于x的方程,解方程即可.
【详解】解:∵,
∴,
∴,
解得,
故选C.
【点睛】本题主要考查了解一元一次方程,正确理解题意是解题的关键.
10.C
【分析】本题考查了解一元一次方程,已知等式利用题中的新定义化简,即可求解,掌握运算法则是解题的关键.
【详解】解:根据题中的新定义化简得:
,
解得:,
故选:C.
11.B
【解析】略
12.D
【分析】把x=2代入方程3x 4= a得到关于a的一元一次方程,解之,将a代入计算求值,即可得到答案.
【详解】解:把x=2代入方程3x 4= a得:
6-4=1-a,
解得:a=-1,
当a=-1时,=(-1)2022=1,
故选:D.
【点睛】本题考查了利用一元一次方程的解求参数,正确掌握解一元一次方程的方法是解题的关键.
13.
【分析】由题意根据任意一行,任意一列及任意一条对角线上的数之和都相等列出方程以及,求出和,即可得出答案.
【详解】解:根据题意得:
,解得:,
,解得:,
∴为,
解得:,
故答案为:.
【点睛】本题考查了一元一次方程的应用,理解“九宫格”满足的条件,进而得到等量关系列出方程是解题的关键.
14.1
【分析】根据解一元一次方程的方法移项合并,把x系数化为1,即可求出解.
【详解】解:2x–1=–5x+6
移项,得2x+5x=1+6,
合并同类项,得7x=7,
系数化为1,得x=1,
故答案为:1.
【点睛】本题主要考查解一元一次方程,解题的关键是掌握解一元一次方程的基本步骤:去分母、去括号、移项、合并同类项、系数化为1.
15.
【分析】本题考查新定义运算,解一元一次方程,根据题意得:,求解即可得出答案.
【详解】解:根据题意得:,
解得:,
故答案为:.
16. 方程 一元一次方程 方程的解
【解析】略
17.4
【分析】根据一元一次方程的定义得出k-3=1,即可得出答案.
【详解】解:由题意得:k-3=1,
解得:k=4,
故答案为:4.
【点睛】本题主要考查了一元一次方程的定义.只含有一个未知数,且未知数的指数是1,一次项系数不是0.
18..
【分析】根据题意可得:,然后解一元一次方即可求解.
【详解】解:∵,,
∴,
移项,合并同类项,得:,
系数化为1,得:
故答案为:.
【点睛】本题考查解一元一次方程,解题的关键是根据新定义正确列出方程,并熟练掌握运用解一元一次方程的步骤.
19.(1)
(2)
【分析】(1)根据去括号,移项,合并,化系数为1的步骤解方程即可;
(2)根据去分母,去括号,移项,合并,化系数为1的步骤解方程即可.
【详解】(1)解:
去括号得:,
移项得:,
合并得:,
化系数为1得:;
(2)解:
去分母得:,
去括号得:,
移项得:,
合并得:,
系数化为1得:.
【点睛】本题主要考查了解一元一次方程,熟知解一元一次方程的方法是解题的关键.
20.(1);(2)
【分析】(1)根据一元一次方程的解题步骤,移项合并同类项,系数化1即可;
(2)根据一元一次方程的解题步骤,移项合并同类项,系数化1即可;
【详解】解:(1)移项,得.
化简,得.
方程两边同除以2,得.
(2)移项,得.
合并同类项,得.
【点睛】本题考查一元一次方程的解法,掌握移项,合并同类项,系数化1是解题关键.
21.(1)
(2)
【详解】(1)解:去分母,得:,
去括号,得:,
移项,合并,得:,
系数化1,得:;
(2)解:去分母,得:,
去括号,得:,
移项,合并,得:,
系数化1,得:.
【点睛】本题考查解一元一次方程.解题的关键是掌握解一元一次方程的步骤,正确的进行计算.
22.
【分析】本题考查的是一元一次方程的解法,掌握解一元一次方程的步骤与方法是解本题的关键.先去括号,再移项,合并同类项,把未知数的系数化1即可.
【详解】解:,
去括号,得:,
移项、合并同类项,得,
系数化为1,得.
23.(1)
(2)
(3)
(4)
【分析】此题考查了解一元一次方程,熟练掌握解一元一次方程的基本步骤及注意事项是解题的关键.
(1)按照去括号、移项、合并同类项、系数化1的步骤解方程即可;
(2)按照去括号、移项、合并同类项、系数化1的步骤解方程即可;
(3)按照去括号、移项、合并同类项、系数化1的步骤解方程即可;
(4)按照去括号、移项、合并同类项、系数化1的步骤解方程即可.
【详解】(1)
去括号得,
移项合并同类项得,
系数化为1得,
(2)
去括号得,
移项合并同类项得,
系数化为1得,
(3)
去括号得,
移项合并同类项得,
系数化为1得,
(4)
去括号得,
移项合并同类项得,
系数化为1得,
24.(1);(2)x=-
【解析】略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.5一元一次方程
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.当k取何值时,与的解相同?( )
A. B. C.4 D.3
2.方程的解是( )
A. B. C. D.
3.方程的解是( ).
A. B. C. D.
4.若关于x的方程是一元一次方程,则a,b应满足的条件是( )
A. B.
C. D.
5.已知与是同类项,则的值是( )
A.12 B.13 C.16 D.17
6.下列解方程变形正确的是( )
A.由得 B.由得
C.由得 D.由得
7.方程x+1=5的解是( )
A.x=﹣6 B.x=6 C.x=4 D.x=﹣4
8.下列方程中,解为的方程是( ).
A. B. C. D.
9.若对于任意实数a,b,c,d,定义,按照定义,若,则x的值为( )
A.1 B. C. D.5
10.对于非零的两个有理数a,b,规定,若,则x的值为( )
A. B. C. D.
11.解方程,去分母正确的是( )
A. B.
C. D.
12.如果是关于的方程的解,则的值是 ( )
A. B.2 C. D.1
二、填空题
13.把这个数填入的方格中,使其任意一行,任意一列及任意一条对角线上的数之和都相等,这样便构成了一个“九宫格”,它源于我国古代的“洛书”(图1),洛书是世界上最早的“幻方”,图是仅可以看到部分数值的“九宫格”,则关于的一元一次方程的解为 .
14.在0,1,2,3中, 是方程2x–1=–5x+6的解.
15.定义新运算:.例如:,那么当时, .
16.含有未知数的等式叫做
只含有一个未知数,并且未知数的次数(即指数)是1,这样的方程叫 .
能使方程左右两边的值相等的未知数的值叫做 .
17.如果是一元一次方程,那么 .
三、解答题
18.定义符号“*”表示的运算法则为,若,求的值.
19.解方程
(1)
(2)
20.解下列方程:
(1);
(2).
21.解下列方程:
(1);
(2).
22.解方程:.
23.解下列方程:
(1)
(2)
(3)
(4)
24.解方程:
(1)3-(4x-3)=7
(2)2x-(x+10)=5x+2(x-1)
《2.5一元一次方程》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D A C C B C C C C C
题号 11 12
答案 B D
1.D
【分析】此题主要考查了同解方程,首先根据解一元一次方程的方法,求出的解是多少;然后把求出的x的值代入,求出k的值是多少即可.
【详解】解:解得,
把代入得,
解得.
故选:D.
2.A
【分析】本题考查解一元一次方程,直接利用系数化为解题即可.
【详解】解:两边同时除以得到,
故选A.
3.C
【解析】略
4.C
【分析】只含有一个未知数(元),且未知数的指数为1的方程叫做一元一次方程,它的一般形式是(a、b是常数,且),根据一元一次方程的定义求出答案.
【详解】解:根据题题意得:,
解得:.
故选:C.
【点睛】本题考查了一元一次方程的一般形式,只含有一个未知数(元),且未知数的指数为1,一次项系数不是0,这是此类题目考查的重点.
5.B
【分析】本题考查同类项的概念、解一元一次方程等,同类项是指所含的字母相同,并且相同字母的指数也分别相同的两个单项式.解题的关键是理解同类项的概念求出的值.
根据同类项的概念列出关于的一元一次方程,解得的值后,代入式子即可得出结论.
【详解】解:与是同类项,
,,
解得:,,
故选:B.
6.C
【分析】根据解一元一次方程的步骤:去分母,去括号,移项,合并同类项,系数化为1逐个检验即可求解.
【详解】解:选项A:方程两边都乘2,即可得到,故本选项错误;
选项B:方程两边都除以3,即可得到,故本选项错误;
选项C:移项得,合并同类项得,系数化为1得,故本选项正确;
选项D.移项得,故本选项错误,
故选:C.
【点睛】本题考查了解一元一次方程的步骤及解法,属于基础题,移项时要记得变号,同时计算过程要细心.
7.C
【分析】方程移项合并,即可求出解.
【详解】解:方程x+1=5,
移项得:x=5-1,
合并得:x=4.
故选:C.
【点睛】此题考查了解一元一次方程,熟练掌握一元一次方程的解法是解本题的关键.
8.C
【分析】本题考查了一元一次方程的解,依次解方程即可.
【详解】A、,解得:,不符合题意,选项错误;
B、,解得:,不符合题意,选项错误;
C、,解得:,符合题意,选项正确;
D、,解得:,不符合题意,选项错误;
故选:C.
9.C
【分析】根据题目所给的新定义得到关于x的方程,解方程即可.
【详解】解:∵,
∴,
∴,
解得,
故选C.
【点睛】本题主要考查了解一元一次方程,正确理解题意是解题的关键.
10.C
【分析】本题考查了解一元一次方程,已知等式利用题中的新定义化简,即可求解,掌握运算法则是解题的关键.
【详解】解:根据题中的新定义化简得:
,
解得:,
故选:C.
11.B
【解析】略
12.D
【分析】把x=2代入方程3x 4= a得到关于a的一元一次方程,解之,将a代入计算求值,即可得到答案.
【详解】解:把x=2代入方程3x 4= a得:
6-4=1-a,
解得:a=-1,
当a=-1时,=(-1)2022=1,
故选:D.
【点睛】本题考查了利用一元一次方程的解求参数,正确掌握解一元一次方程的方法是解题的关键.
13.
【分析】由题意根据任意一行,任意一列及任意一条对角线上的数之和都相等列出方程以及,求出和,即可得出答案.
【详解】解:根据题意得:
,解得:,
,解得:,
∴为,
解得:,
故答案为:.
【点睛】本题考查了一元一次方程的应用,理解“九宫格”满足的条件,进而得到等量关系列出方程是解题的关键.
14.1
【分析】根据解一元一次方程的方法移项合并,把x系数化为1,即可求出解.
【详解】解:2x–1=–5x+6
移项,得2x+5x=1+6,
合并同类项,得7x=7,
系数化为1,得x=1,
故答案为:1.
【点睛】本题主要考查解一元一次方程,解题的关键是掌握解一元一次方程的基本步骤:去分母、去括号、移项、合并同类项、系数化为1.
15.
【分析】本题考查新定义运算,解一元一次方程,根据题意得:,求解即可得出答案.
【详解】解:根据题意得:,
解得:,
故答案为:.
16. 方程 一元一次方程 方程的解
【解析】略
17.4
【分析】根据一元一次方程的定义得出k-3=1,即可得出答案.
【详解】解:由题意得:k-3=1,
解得:k=4,
故答案为:4.
【点睛】本题主要考查了一元一次方程的定义.只含有一个未知数,且未知数的指数是1,一次项系数不是0.
18..
【分析】根据题意可得:,然后解一元一次方即可求解.
【详解】解:∵,,
∴,
移项,合并同类项,得:,
系数化为1,得:
故答案为:.
【点睛】本题考查解一元一次方程,解题的关键是根据新定义正确列出方程,并熟练掌握运用解一元一次方程的步骤.
19.(1)
(2)
【分析】(1)根据去括号,移项,合并,化系数为1的步骤解方程即可;
(2)根据去分母,去括号,移项,合并,化系数为1的步骤解方程即可.
【详解】(1)解:
去括号得:,
移项得:,
合并得:,
化系数为1得:;
(2)解:
去分母得:,
去括号得:,
移项得:,
合并得:,
系数化为1得:.
【点睛】本题主要考查了解一元一次方程,熟知解一元一次方程的方法是解题的关键.
20.(1);(2)
【分析】(1)根据一元一次方程的解题步骤,移项合并同类项,系数化1即可;
(2)根据一元一次方程的解题步骤,移项合并同类项,系数化1即可;
【详解】解:(1)移项,得.
化简,得.
方程两边同除以2,得.
(2)移项,得.
合并同类项,得.
【点睛】本题考查一元一次方程的解法,掌握移项,合并同类项,系数化1是解题关键.
21.(1)
(2)
【详解】(1)解:去分母,得:,
去括号,得:,
移项,合并,得:,
系数化1,得:;
(2)解:去分母,得:,
去括号,得:,
移项,合并,得:,
系数化1,得:.
【点睛】本题考查解一元一次方程.解题的关键是掌握解一元一次方程的步骤,正确的进行计算.
22.
【分析】本题考查的是一元一次方程的解法,掌握解一元一次方程的步骤与方法是解本题的关键.先去括号,再移项,合并同类项,把未知数的系数化1即可.
【详解】解:,
去括号,得:,
移项、合并同类项,得,
系数化为1,得.
23.(1)
(2)
(3)
(4)
【分析】此题考查了解一元一次方程,熟练掌握解一元一次方程的基本步骤及注意事项是解题的关键.
(1)按照去括号、移项、合并同类项、系数化1的步骤解方程即可;
(2)按照去括号、移项、合并同类项、系数化1的步骤解方程即可;
(3)按照去括号、移项、合并同类项、系数化1的步骤解方程即可;
(4)按照去括号、移项、合并同类项、系数化1的步骤解方程即可.
【详解】(1)
去括号得,
移项合并同类项得,
系数化为1得,
(2)
去括号得,
移项合并同类项得,
系数化为1得,
(3)
去括号得,
移项合并同类项得,
系数化为1得,
(4)
去括号得,
移项合并同类项得,
系数化为1得,
24.(1);(2)x=-
【解析】略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
