2.6列方程解决实际问题暑假预习练(含解析) 北京版数学七年级上册
文档属性
| 名称 | 2.6列方程解决实际问题暑假预习练(含解析) 北京版数学七年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 598.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-09 11:28:14 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2.6列方程解决实际问题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某商场将一种商品按成本价提高后标价,八折销售,每件仍获利元,设这种商品的成本价为元,根据题意所列方程正确的是( )
A. B.
C. D.
2.《九章算术》中有这样一道题:“今有善行者行一百步,不善行者行六十步.今不善行者先行一百步,善行者追之,问几何步及之?”译文:“相同时间内,走路快的人走100步,走路慢的人只走60步.若走路慢的人先走100步,走路快的人要走多少步才能追上?(注:步为长度单位)“设走路快的人要走x步才能追上,则正确的是( )
A.依题意 B.依题意
C.走路快的人要走200步才能追上 D.从走路快的人出发时开始算,当走路慢的人再走600步后,两人相隔400步
3.如图,正方形的一边长减少后,得到一个长方形(图中阴影部分),若长方形的周长为,求正方形的边长.设正方形的边长为,可列方程为( )
A. B. C. D.
4.《孙子算经》中有这样一道题,原文如下:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽.问:城中家几何?大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的每3家共取一头,恰好取完.问城中有多少户人家?( )
A.55户 B.65户 C.75户 D.85户
5.幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格,将个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的个数之和相等,图①就是一个幻方.图②是一个未完成的幻方,则的值是( )
A. B. C. D.
6.某个体商贩在一次买卖中,同时卖出两件上衣,售价都是60元,若按成本计,其中一件盈利25%,另一件亏本25%,在这次买卖中他( )
A.赚7元 B.赚8元 C.赔7元 D.赔8元
7.我国古代数学名著《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四,问人数,物价各几何?”意思是现有几个人共买一件物品,每人出8钱.多出3钱;每人出7钱,差4钱.问人数,物价各是多少?若设共有人,物价是钱,则下列方程正确的是( )
A. B.
C. D.
8.某个体商贩在一次买卖中,同时卖出两件上衣,售价都是135元,若按成本计,其中一件盈利,另一件亏本,在这次买卖中他( )
A.不赚不赔 B.赔18元 C.赚18元 D.赚9元
9.某车间有35名工人生产螺栓和螺母,每人每天平均生产12个螺栓或18个螺母.已知1个螺栓配2个螺母,要使当天生产的螺栓和螺母刚好配套,则应安排生产螺栓的工人人数为( )
A.13 B.14 C.15 D.16
10.我国古代有很多经典的数学题,其中有一道题目是:良马日行二百里,驽马日行一百二十里,驽马先行十日,问良马几何追及之.意思是:跑得快的马每天走200里,跑得慢的马每天走120里,慢马先走10天,快马几天可追上慢马?若设快马天可追上慢马,则由题意可列方程为( )
A. B.
C. D.
11.一商店在某一时间以每件60元的价格卖出两只书包,其中一只盈利,另一只亏损,则卖出这两只书包总的盈亏情况是()
A.盈利5元 B.亏损5元 C.亏损8元 D.不盈不亏
12.将进价为120元一盒的某品牌粽子按标价的8折出售,仍可获利20%,则该超市该品牌粽子的标价为( )元
A.180 B.170 C.160 D.150
二、填空题
13.某店铺举行庆新年促销活动,将一批进价为80元/条的短裤按标价的八折出售,每条短裤的利润率为,则这批短裤每条的标价为 元.
14.文化体验
合并同类项的来源
公元820年左右,中亚细亚数学家阿尔一花拉子米写了一本代数书,重点论述怎样解方程.这本书的拉丁文译本取名为《对消与还原》.顾名思义,就是将方程中各项成对消除的意思.相当于现代解方程中的“合并同类项”.在我国也有相同的著作,明代数学家吴敬所著的《九章算术比类大全》中,有一道数学名题叫“宝塔装灯”,内容为“远望巍巍塔七层,红灯点点倍加增,共灯三百八十一,请问:顶层几盏灯?”(倍加增指从塔的顶层到底层加倍递增).请你算出塔的顶层有 盏灯.
15.有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地.若求此人第六天走的路程为多少里.设此人第六天走的路程为x里,依题意,可列方程为 .
16.在元朝朱世杰所著的《算术启蒙》中,记载了一道题,大意是:快马每天行240里,慢马每天行150里,慢马先行12天,则快马追上慢马需要的天数是 .
17.今年端午节前某超市分两次购进蛋黄、鲜肉、腊肉三种馅的粽子,第一次购进三种粽子数量之比为 3∶ 2∶ 1.根据销量,超市调整进货方案, 第一次与第二次购进蛋黄粽数量之比为 3∶ 4,且第二次购进蛋黄粽数量为第二次购进总量的 .为使两次购进鲜肉粽和腊肉粽数量之比为 ,则第二次购进鲜肉粽和腊肉粽数量之比为 .
三、解答题
18.新农村建设中,某镇成立了新型农业合作社,扩大了油菜种植面积,今年2000亩油菜喜获丰收.该合作社计划租赁5台油菜收割机机械化收割,一台收割机每天大约能收割40亩油菜.
(1)求该合作社按计划几天可收割完这些油菜;
(2)该合作社在完成了一半收割任务时,从气象部门得知三天后有降雨,于是该合作社决定再租赁3台油菜收割机加入抢收,并把每天的工作时间延长10%,请判断该合作社能否完成抢收任务,并说明理由.
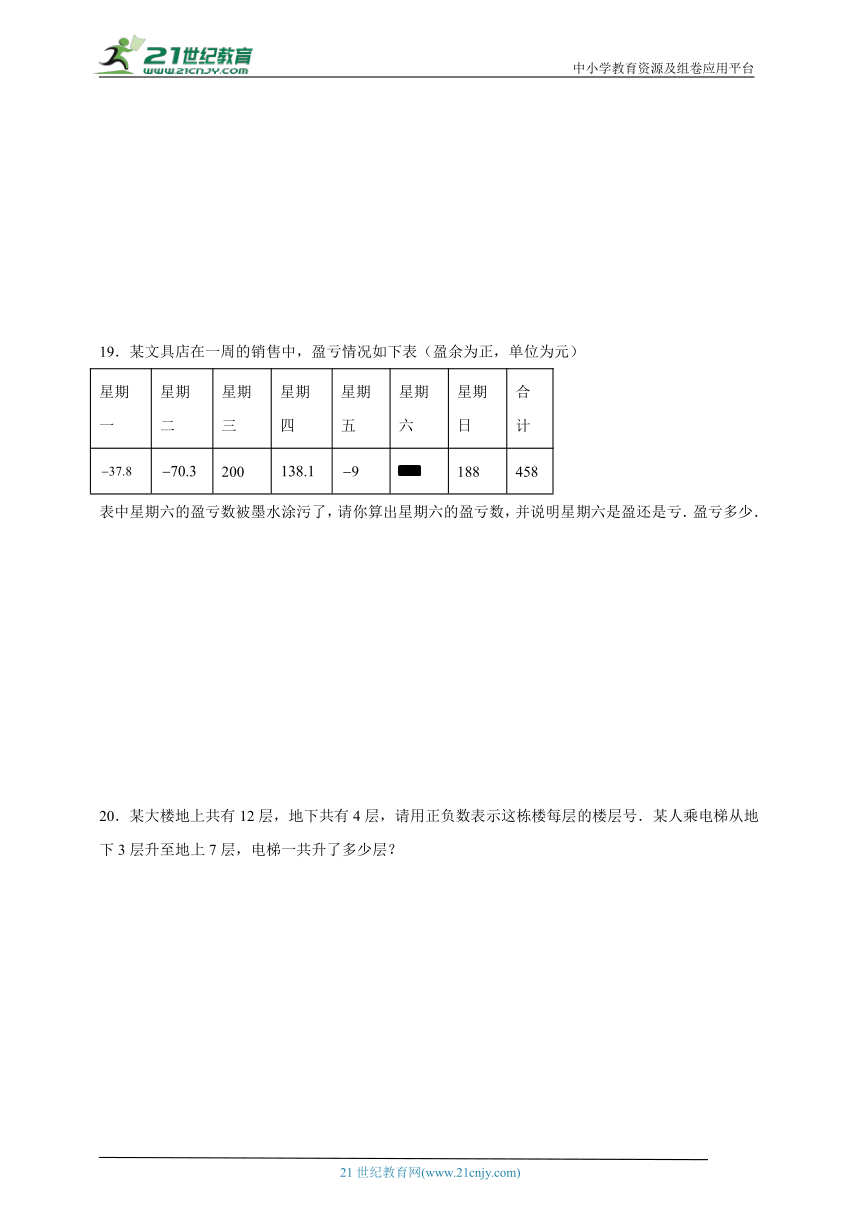
19.某文具店在一周的销售中,盈亏情况如下表(盈余为正,单位为元)
星期一 星期二 星期三 星期四 星期五 星期六 星期日 合计
200 188 458
表中星期六的盈亏数被墨水涂污了,请你算出星期六的盈亏数,并说明星期六是盈还是亏.盈亏多少.
20.某大楼地上共有12层,地下共有4层,请用正负数表示这栋楼每层的楼层号.某人乘电梯从地下3层升至地上7层,电梯一共升了多少层?
21.有某种三色冰淇淋50g,咖啡色 红色和白色配料的比是2∶3∶5,这种三色冰淇淋中咖啡色 红色和白色配料分别是多少克?
22.下面的表格是某次篮球联赛积分表:
某次篮球联赛积分表
队名 比赛场次 胜场 负场 积分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
(1)如果删去积分表的最后一行,你能求出胜一场和负一场的得分吗?
(2)某队的胜场总积分能等于它的负场总积分的2倍吗?
(3)某队的负场总积分能等于它的胜场总积分的2倍吗?
23.如图,依依与爸爸在下围棋,棋盘旁有甲、乙两个围棋盒.甲盒中都是黑子,共12个;乙盒中都是白子,共9个.依依从甲盒中拿出a个黑子放入乙盒,使乙盒棋子总数是甲盒所剩棋子数的2倍,求a的值.
24.中国古代数学著作《算法统宗》中有这样一段记载,“三百七十八里关;初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是;有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到关口,求此人第一和第六这两天共走的路程.
《2.6列方程解决实际问题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B D C B D D B C D
题号 11 12
答案 B A
1.B
【分析】此题主要考查了由实际问题抽象出一元一次方程,关键是正确理解题意,掌握利润、进价、售价之间的关系.首先设这种服装每件的成本价是元,根据题意可得等量关系:进价折成本利润元,根据等量关系列出方程即可.
【详解】解:设这种商品的成本价为元,
根据题意得:
故选:B.
2.B
【分析】设走路快的人要走x步才能追上,由走路快的人走x步所用时间内比走路慢的人多行100步,即可得出关于x的一元一次方程,此题得解.
【详解】解:设走路快的人要走x步才能追上,则走路慢的人走,
依题意,得:.
故选:B.
【点睛】本题考查了由实际问题抽象出一元一次方程以及数学常识,找准等量关系,正确列出一元一次方程是解题的关键.
3.D
【分析】本题主要考查一元一次方程解几何问题,根据长方形边长与正方形边长的关系列式即可求解,掌握一元一次方程的实际运用是解题的关键.
【详解】解:设正方形的边长为,
∴,
故选:C.
4.C
【分析】设城中有户人家,由题意列一元一次方程,解一元一次方程即可解题.
【详解】解:设城中有户人家,根据题意得,
解得
故选:C.
【点睛】本题考查一元一次方程的实际应用,是重要考点,难度较易,掌握相关知识是解题关键.
5.B
【分析】本题考查了一元一次方程的应用,读懂题意,找出等量关系列出方程是解题的关键;
设图②中间的数为,第三行第一数为,根据题意列出方程,求解即可;
【详解】解:设图②中间的数为,第三行第一数为,
由题意,可得:;
由①得:;
由②得:;
所以;
解得:;
所以;
故选:A
6.D
【分析】设盈利的上衣的进价为x元,亏损的上衣的进价为y元,根据利润=销售收入成本,即可得出关于x(或y)的一元一次方程,解之即可得出两件上衣的成本,再利用总利润=两件上衣的总售价 两件上衣的总成本即可求出结论.
【详解】解:设盈利的上衣的成本为x元,亏损的上衣的成本为y元,
依题意,得:,,
解得:,
∵(元).
∴该商贩亏损8元.
故选:D.
【点睛】本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.
7.D
【分析】设共有x人,根据物价不变列方程;设物价是钱,根据人数不变即可列出一元一次方程;由此即可确定正确答案
【详解】解:设共有x人,则有8x-3=7x+4
设物价是钱,则根据可得:
故选D.
【点睛】本题主要考查了列一元一次方程,正确审题、发现隐藏的等量关系成为解答本题的关键.
8.B
【分析】本题主要考查了一元一次方程,解题的关键是先算出两件衣服的原价,要算出原价就要先设出未知数,然后根据题中的等量关系列方程,再解方程.
【详解】解:设在这次买卖中盈利的上衣的原价是x元,
则可列方程:,
解得:
设亏本的上衣的原价为y元,
则可列方程:,
解得:,
∵(元),
∴两件相比则一共赔了元.
故选:B.
9.C
【分析】本题考查了一元一次方程的应用,根据题意正确列出方程是解题的关键.
设安排人生产螺栓,则有人生产螺母,根据题意得到,求解即可.
【详解】解:设安排人生产螺栓,则有人生产螺母,
根据题意得:,
解得:,
应安排生产螺栓的工人人数为,
故选:C.
10.D
【分析】本题考查了一元一次方程的应用;找准等量关系,建立方程是本题的关键.根据慢马与快马所走的路程相等建立方程即可.
【详解】解:设快马天可以追上慢马,
依题意,得:.
故选:D.
11.B
【分析】根据等量关系式分别列方程求出每只书包的原件即可.
【详解】解:设第一只书包的原价为元,
根据题意,得
,
解得;
设第二只书包的原价为元,
根据题意,得
,
解得;
∵,
∴亏损5元,
故选:B
【点睛】本题考查了一元一次方程的应用,求出每只书包的原价是解题的关键.
12.A
【分析】设标价为x,由题意找到等量关系列出方程解出答案即可.
【详解】解:设该超市该品牌粽子的标价为x元,则售价为80%x元,
由题意得:80%x-120=20%×120,
解得:x=180.
即该超市该品牌粽子的标价为180元.
故选:A.
【点睛】本题主要考查了一元一次方程的实际应用,找到等量关系是解题的关键.
13.120
【分析】设这批短裤每条的标价为元,根据题意列方程求解,即可得到答案.
【详解】解:设这批短裤每条的标价为元,
由题意得:,
解得:,
即这批短裤每条的标价为120元,
故答案为:120.
【点睛】本题考查了一元一次方程的实际应用,根据题意正确列方程是解题关键.
14.3
【分析】要求塔的顶层有几盏灯,就要先设出求知数,再根据倍加增求出各层的灯数,然后根据共灯三百八十一的等量关系列出方程求解.
【详解】解:设顶层有盏灯.
根据题意得:,
解得:.
因此塔的顶层有3盏灯.
故答案为:3.
【点睛】本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.
15.
【分析】设此人第六天走的路程为里,则可以表示出前五天走的路程,加起来即可得解;
【详解】设此人第六天走的路程为里,则前五天走的路程分别为,,,,里,依题意得:;
故答案是:.
【点睛】本题主要考查了一元一次方程的应用,准确分析列方程是解题的关键.
16.20
【详解】设快马追上慢马需要的天数是x,根据题意得,解得,
∴快马需要20天追上慢马.
17.
【分析】设第一次购进蛋黄粽子3x个,则购进鲜肉粽子2x个,腊肉粽子x个,第二次购进蛋黄粽子4x个,求出第二次的购进总量为9x个,然后设第二次购进鲜肉粽子mx个,则购进腊肉粽子(5-m)x个,再根据两次购进鲜肉粽和腊肉粽数量之比为 列式求出m的值,进而得到答案.
【详解】解:设第一次购进蛋黄粽子3x个,则购进鲜肉粽子2x个,腊肉粽子x个,第二次购进蛋黄粽子4x个,
∵第二次购进蛋黄粽子数量为第二次购进总量的,
∴第二次的购进总量为4x÷=9x个,
∴第二次购进鲜肉粽子和腊肉粽子共5x个,
设第二次购进鲜肉粽子mx个,则购进腊肉粽子(5-m)x个,
由题意得:,
解得:,
∴5-m=,
∴第二次购进鲜肉粽和腊肉粽数量之比为:,
故答案为:.
【点睛】本题考查了一元一次方程的应用,能够根据题意得出各数据之间的关系并正确列出方程是解题的关键.
18.(1)该合作社按计划10天可收割完这些油菜
(2)该合作社能完成抢收任务,理由见解析
【分析】(1)设该合作社按计划天可收割完这些油菜,再根据“工作效率工作时间=工作总量”列一元一次方程并解答即可;
(2)先求出增加3台油菜收割机后一天的收割量,再求出三天的收割量,然后和1000亩进行比较即可.
【详解】(1)解:设该合作社按计划天可收割完这些油菜
解得:
答:该合作社按计划10天可收割完这些油菜;
(2)解:原来一天的收割量:(亩),
现在一天的收割量:(亩),
现在三天可完成的收割量:(亩)亩.
答:该合作社能完成抢收任务.
【点睛】本题考查了一元一次方程应用中的工程问题,找到等量关系是解答本题的关键.
19.盈利49元
【分析】本题主要考查了一元一次方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.正确理解正负数的意义;设星期六为元,根据题意可得等量关系:七天的盈亏数之和,根据等量关系列出方程,再解方程即可.
【详解】解:设星期六为元,则:,
,
,
因为49为正数,故星期六是盈利,盈利49元,
答:星期六是盈利49元.
20.电梯一共升了10层
【分析】将上升记为“+”,下降记为“-”,地下楼层记为负数楼层,地上楼层记为正数楼层,依题意列式即可.
【详解】解:设电梯一共升了x层,
依题意,得-3+x=7
解得x=10
答:电梯一共升了10层.
【点睛】本题考查了一元一次方程的应用及正负数的表示,熟练应用正负数去表示生活中的场景是解决本题的关键.
21.咖啡色 红色和白色配料分别是,和
【分析】可设比中每一份为x,那么可得用x表示的三种颜色的冰淇淋的质量,让这3个质量之和=50,把相关数值代入求解即可.
【详解】解:设这种三色冰淇淋中咖啡色配料为,那么红色和白色配料分别为和.
根据题意,得,
解得,
则, ,.
则这种三色冰淇淋中咖啡色 红色和白色配料分别是,和.
【点睛】考查一元一次方程的应用,得到冰淇淋质量和的等量关系是解决本题的关键;注意有比的问题应设比中的每一份为x.
22.(1)胜1场得2分,负1场得1分
(2)某队的胜场总积分能等于它的负场总积分的2倍
(3)不能,详见解析
【分析】(1)利用东方队和光明队的数据设胜1场得分,则东方队负场总积分为分,可得负1场得分;光明队负场总积分为分,可得负1场得分,再建立方程求解即可;
(2)设一个队胜的场次为,则负的场次为,再根据胜场总积分能等于它的负场总积分的2倍,再列方程求解即可;
(3)设一个队胜的场次为,则负的场次为,再根据负场总积分能等于它的胜场总积分的2倍,再列方程求解即可.
【详解】(1)解:能.利用东方队和光明队的数据设胜1场得分,
则东方队负场总积分为分,
∴负1场得分;
光明队负场总积分为分,
∴负1场得分.
由此得方程,
解得.
则.
答:胜1场得2分,负1场得1分.
(2)能.设一个队胜的场次为,则负的场次为.
由题意,得,
解得.
所以某队的胜场总积分能等于它的负场总积分的2倍.
(3)不能.设一个队胜的场次为,则负的场次为.
由题意,得,
解得.
因为胜的场次不可能为分数,所以某队的负场总积分不能等于它的胜场总积分的2倍
【点睛】本题考查的是一元一次方程的应用,理解题意,准确的确定相等关系并列方程是解本题的关键.
23.5
【分析】从甲盒中拿出a个黑子放入乙盒,那么甲盒的棋子数为个,乙盒的棋子数为个,再根据乙盒棋子总数是甲盒所剩棋子数的2倍列出方程求解即可.
【详解】解:由题意得,,
解得,
∴a的值为5.
【点睛】本题主要考查了一元一次方程的实际应用,正确理解题意找到等量关系列出方程是解题的关键.
24.198里
【分析】设第六天走的路程为x里,则第五天走的路程为里,依次往前推,第一天走的路程为里,根据每天的路程加起来为378里,列方程即可解答.
【详解】解:设第六天走的路程为x里,则第五天走的路程为里,
依此往前推,第一天走的路程为里,
依题意,得:,
解得:,
,(里),
答:此人第一和第六这两天共走了198里.
【点睛】本题考查了一元一次方程的实际应用,正确地用未知数表示每一天走的路程是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.6列方程解决实际问题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某商场将一种商品按成本价提高后标价,八折销售,每件仍获利元,设这种商品的成本价为元,根据题意所列方程正确的是( )
A. B.
C. D.
2.《九章算术》中有这样一道题:“今有善行者行一百步,不善行者行六十步.今不善行者先行一百步,善行者追之,问几何步及之?”译文:“相同时间内,走路快的人走100步,走路慢的人只走60步.若走路慢的人先走100步,走路快的人要走多少步才能追上?(注:步为长度单位)“设走路快的人要走x步才能追上,则正确的是( )
A.依题意 B.依题意
C.走路快的人要走200步才能追上 D.从走路快的人出发时开始算,当走路慢的人再走600步后,两人相隔400步
3.如图,正方形的一边长减少后,得到一个长方形(图中阴影部分),若长方形的周长为,求正方形的边长.设正方形的边长为,可列方程为( )
A. B. C. D.
4.《孙子算经》中有这样一道题,原文如下:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽.问:城中家几何?大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的每3家共取一头,恰好取完.问城中有多少户人家?( )
A.55户 B.65户 C.75户 D.85户
5.幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格,将个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的个数之和相等,图①就是一个幻方.图②是一个未完成的幻方,则的值是( )
A. B. C. D.
6.某个体商贩在一次买卖中,同时卖出两件上衣,售价都是60元,若按成本计,其中一件盈利25%,另一件亏本25%,在这次买卖中他( )
A.赚7元 B.赚8元 C.赔7元 D.赔8元
7.我国古代数学名著《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四,问人数,物价各几何?”意思是现有几个人共买一件物品,每人出8钱.多出3钱;每人出7钱,差4钱.问人数,物价各是多少?若设共有人,物价是钱,则下列方程正确的是( )
A. B.
C. D.
8.某个体商贩在一次买卖中,同时卖出两件上衣,售价都是135元,若按成本计,其中一件盈利,另一件亏本,在这次买卖中他( )
A.不赚不赔 B.赔18元 C.赚18元 D.赚9元
9.某车间有35名工人生产螺栓和螺母,每人每天平均生产12个螺栓或18个螺母.已知1个螺栓配2个螺母,要使当天生产的螺栓和螺母刚好配套,则应安排生产螺栓的工人人数为( )
A.13 B.14 C.15 D.16
10.我国古代有很多经典的数学题,其中有一道题目是:良马日行二百里,驽马日行一百二十里,驽马先行十日,问良马几何追及之.意思是:跑得快的马每天走200里,跑得慢的马每天走120里,慢马先走10天,快马几天可追上慢马?若设快马天可追上慢马,则由题意可列方程为( )
A. B.
C. D.
11.一商店在某一时间以每件60元的价格卖出两只书包,其中一只盈利,另一只亏损,则卖出这两只书包总的盈亏情况是()
A.盈利5元 B.亏损5元 C.亏损8元 D.不盈不亏
12.将进价为120元一盒的某品牌粽子按标价的8折出售,仍可获利20%,则该超市该品牌粽子的标价为( )元
A.180 B.170 C.160 D.150
二、填空题
13.某店铺举行庆新年促销活动,将一批进价为80元/条的短裤按标价的八折出售,每条短裤的利润率为,则这批短裤每条的标价为 元.
14.文化体验
合并同类项的来源
公元820年左右,中亚细亚数学家阿尔一花拉子米写了一本代数书,重点论述怎样解方程.这本书的拉丁文译本取名为《对消与还原》.顾名思义,就是将方程中各项成对消除的意思.相当于现代解方程中的“合并同类项”.在我国也有相同的著作,明代数学家吴敬所著的《九章算术比类大全》中,有一道数学名题叫“宝塔装灯”,内容为“远望巍巍塔七层,红灯点点倍加增,共灯三百八十一,请问:顶层几盏灯?”(倍加增指从塔的顶层到底层加倍递增).请你算出塔的顶层有 盏灯.
15.有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地.若求此人第六天走的路程为多少里.设此人第六天走的路程为x里,依题意,可列方程为 .
16.在元朝朱世杰所著的《算术启蒙》中,记载了一道题,大意是:快马每天行240里,慢马每天行150里,慢马先行12天,则快马追上慢马需要的天数是 .
17.今年端午节前某超市分两次购进蛋黄、鲜肉、腊肉三种馅的粽子,第一次购进三种粽子数量之比为 3∶ 2∶ 1.根据销量,超市调整进货方案, 第一次与第二次购进蛋黄粽数量之比为 3∶ 4,且第二次购进蛋黄粽数量为第二次购进总量的 .为使两次购进鲜肉粽和腊肉粽数量之比为 ,则第二次购进鲜肉粽和腊肉粽数量之比为 .
三、解答题
18.新农村建设中,某镇成立了新型农业合作社,扩大了油菜种植面积,今年2000亩油菜喜获丰收.该合作社计划租赁5台油菜收割机机械化收割,一台收割机每天大约能收割40亩油菜.
(1)求该合作社按计划几天可收割完这些油菜;
(2)该合作社在完成了一半收割任务时,从气象部门得知三天后有降雨,于是该合作社决定再租赁3台油菜收割机加入抢收,并把每天的工作时间延长10%,请判断该合作社能否完成抢收任务,并说明理由.
19.某文具店在一周的销售中,盈亏情况如下表(盈余为正,单位为元)
星期一 星期二 星期三 星期四 星期五 星期六 星期日 合计
200 188 458
表中星期六的盈亏数被墨水涂污了,请你算出星期六的盈亏数,并说明星期六是盈还是亏.盈亏多少.
20.某大楼地上共有12层,地下共有4层,请用正负数表示这栋楼每层的楼层号.某人乘电梯从地下3层升至地上7层,电梯一共升了多少层?
21.有某种三色冰淇淋50g,咖啡色 红色和白色配料的比是2∶3∶5,这种三色冰淇淋中咖啡色 红色和白色配料分别是多少克?
22.下面的表格是某次篮球联赛积分表:
某次篮球联赛积分表
队名 比赛场次 胜场 负场 积分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
(1)如果删去积分表的最后一行,你能求出胜一场和负一场的得分吗?
(2)某队的胜场总积分能等于它的负场总积分的2倍吗?
(3)某队的负场总积分能等于它的胜场总积分的2倍吗?
23.如图,依依与爸爸在下围棋,棋盘旁有甲、乙两个围棋盒.甲盒中都是黑子,共12个;乙盒中都是白子,共9个.依依从甲盒中拿出a个黑子放入乙盒,使乙盒棋子总数是甲盒所剩棋子数的2倍,求a的值.
24.中国古代数学著作《算法统宗》中有这样一段记载,“三百七十八里关;初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是;有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到关口,求此人第一和第六这两天共走的路程.
《2.6列方程解决实际问题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B D C B D D B C D
题号 11 12
答案 B A
1.B
【分析】此题主要考查了由实际问题抽象出一元一次方程,关键是正确理解题意,掌握利润、进价、售价之间的关系.首先设这种服装每件的成本价是元,根据题意可得等量关系:进价折成本利润元,根据等量关系列出方程即可.
【详解】解:设这种商品的成本价为元,
根据题意得:
故选:B.
2.B
【分析】设走路快的人要走x步才能追上,由走路快的人走x步所用时间内比走路慢的人多行100步,即可得出关于x的一元一次方程,此题得解.
【详解】解:设走路快的人要走x步才能追上,则走路慢的人走,
依题意,得:.
故选:B.
【点睛】本题考查了由实际问题抽象出一元一次方程以及数学常识,找准等量关系,正确列出一元一次方程是解题的关键.
3.D
【分析】本题主要考查一元一次方程解几何问题,根据长方形边长与正方形边长的关系列式即可求解,掌握一元一次方程的实际运用是解题的关键.
【详解】解:设正方形的边长为,
∴,
故选:C.
4.C
【分析】设城中有户人家,由题意列一元一次方程,解一元一次方程即可解题.
【详解】解:设城中有户人家,根据题意得,
解得
故选:C.
【点睛】本题考查一元一次方程的实际应用,是重要考点,难度较易,掌握相关知识是解题关键.
5.B
【分析】本题考查了一元一次方程的应用,读懂题意,找出等量关系列出方程是解题的关键;
设图②中间的数为,第三行第一数为,根据题意列出方程,求解即可;
【详解】解:设图②中间的数为,第三行第一数为,
由题意,可得:;
由①得:;
由②得:;
所以;
解得:;
所以;
故选:A
6.D
【分析】设盈利的上衣的进价为x元,亏损的上衣的进价为y元,根据利润=销售收入成本,即可得出关于x(或y)的一元一次方程,解之即可得出两件上衣的成本,再利用总利润=两件上衣的总售价 两件上衣的总成本即可求出结论.
【详解】解:设盈利的上衣的成本为x元,亏损的上衣的成本为y元,
依题意,得:,,
解得:,
∵(元).
∴该商贩亏损8元.
故选:D.
【点睛】本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.
7.D
【分析】设共有x人,根据物价不变列方程;设物价是钱,根据人数不变即可列出一元一次方程;由此即可确定正确答案
【详解】解:设共有x人,则有8x-3=7x+4
设物价是钱,则根据可得:
故选D.
【点睛】本题主要考查了列一元一次方程,正确审题、发现隐藏的等量关系成为解答本题的关键.
8.B
【分析】本题主要考查了一元一次方程,解题的关键是先算出两件衣服的原价,要算出原价就要先设出未知数,然后根据题中的等量关系列方程,再解方程.
【详解】解:设在这次买卖中盈利的上衣的原价是x元,
则可列方程:,
解得:
设亏本的上衣的原价为y元,
则可列方程:,
解得:,
∵(元),
∴两件相比则一共赔了元.
故选:B.
9.C
【分析】本题考查了一元一次方程的应用,根据题意正确列出方程是解题的关键.
设安排人生产螺栓,则有人生产螺母,根据题意得到,求解即可.
【详解】解:设安排人生产螺栓,则有人生产螺母,
根据题意得:,
解得:,
应安排生产螺栓的工人人数为,
故选:C.
10.D
【分析】本题考查了一元一次方程的应用;找准等量关系,建立方程是本题的关键.根据慢马与快马所走的路程相等建立方程即可.
【详解】解:设快马天可以追上慢马,
依题意,得:.
故选:D.
11.B
【分析】根据等量关系式分别列方程求出每只书包的原件即可.
【详解】解:设第一只书包的原价为元,
根据题意,得
,
解得;
设第二只书包的原价为元,
根据题意,得
,
解得;
∵,
∴亏损5元,
故选:B
【点睛】本题考查了一元一次方程的应用,求出每只书包的原价是解题的关键.
12.A
【分析】设标价为x,由题意找到等量关系列出方程解出答案即可.
【详解】解:设该超市该品牌粽子的标价为x元,则售价为80%x元,
由题意得:80%x-120=20%×120,
解得:x=180.
即该超市该品牌粽子的标价为180元.
故选:A.
【点睛】本题主要考查了一元一次方程的实际应用,找到等量关系是解题的关键.
13.120
【分析】设这批短裤每条的标价为元,根据题意列方程求解,即可得到答案.
【详解】解:设这批短裤每条的标价为元,
由题意得:,
解得:,
即这批短裤每条的标价为120元,
故答案为:120.
【点睛】本题考查了一元一次方程的实际应用,根据题意正确列方程是解题关键.
14.3
【分析】要求塔的顶层有几盏灯,就要先设出求知数,再根据倍加增求出各层的灯数,然后根据共灯三百八十一的等量关系列出方程求解.
【详解】解:设顶层有盏灯.
根据题意得:,
解得:.
因此塔的顶层有3盏灯.
故答案为:3.
【点睛】本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.
15.
【分析】设此人第六天走的路程为里,则可以表示出前五天走的路程,加起来即可得解;
【详解】设此人第六天走的路程为里,则前五天走的路程分别为,,,,里,依题意得:;
故答案是:.
【点睛】本题主要考查了一元一次方程的应用,准确分析列方程是解题的关键.
16.20
【详解】设快马追上慢马需要的天数是x,根据题意得,解得,
∴快马需要20天追上慢马.
17.
【分析】设第一次购进蛋黄粽子3x个,则购进鲜肉粽子2x个,腊肉粽子x个,第二次购进蛋黄粽子4x个,求出第二次的购进总量为9x个,然后设第二次购进鲜肉粽子mx个,则购进腊肉粽子(5-m)x个,再根据两次购进鲜肉粽和腊肉粽数量之比为 列式求出m的值,进而得到答案.
【详解】解:设第一次购进蛋黄粽子3x个,则购进鲜肉粽子2x个,腊肉粽子x个,第二次购进蛋黄粽子4x个,
∵第二次购进蛋黄粽子数量为第二次购进总量的,
∴第二次的购进总量为4x÷=9x个,
∴第二次购进鲜肉粽子和腊肉粽子共5x个,
设第二次购进鲜肉粽子mx个,则购进腊肉粽子(5-m)x个,
由题意得:,
解得:,
∴5-m=,
∴第二次购进鲜肉粽和腊肉粽数量之比为:,
故答案为:.
【点睛】本题考查了一元一次方程的应用,能够根据题意得出各数据之间的关系并正确列出方程是解题的关键.
18.(1)该合作社按计划10天可收割完这些油菜
(2)该合作社能完成抢收任务,理由见解析
【分析】(1)设该合作社按计划天可收割完这些油菜,再根据“工作效率工作时间=工作总量”列一元一次方程并解答即可;
(2)先求出增加3台油菜收割机后一天的收割量,再求出三天的收割量,然后和1000亩进行比较即可.
【详解】(1)解:设该合作社按计划天可收割完这些油菜
解得:
答:该合作社按计划10天可收割完这些油菜;
(2)解:原来一天的收割量:(亩),
现在一天的收割量:(亩),
现在三天可完成的收割量:(亩)亩.
答:该合作社能完成抢收任务.
【点睛】本题考查了一元一次方程应用中的工程问题,找到等量关系是解答本题的关键.
19.盈利49元
【分析】本题主要考查了一元一次方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.正确理解正负数的意义;设星期六为元,根据题意可得等量关系:七天的盈亏数之和,根据等量关系列出方程,再解方程即可.
【详解】解:设星期六为元,则:,
,
,
因为49为正数,故星期六是盈利,盈利49元,
答:星期六是盈利49元.
20.电梯一共升了10层
【分析】将上升记为“+”,下降记为“-”,地下楼层记为负数楼层,地上楼层记为正数楼层,依题意列式即可.
【详解】解:设电梯一共升了x层,
依题意,得-3+x=7
解得x=10
答:电梯一共升了10层.
【点睛】本题考查了一元一次方程的应用及正负数的表示,熟练应用正负数去表示生活中的场景是解决本题的关键.
21.咖啡色 红色和白色配料分别是,和
【分析】可设比中每一份为x,那么可得用x表示的三种颜色的冰淇淋的质量,让这3个质量之和=50,把相关数值代入求解即可.
【详解】解:设这种三色冰淇淋中咖啡色配料为,那么红色和白色配料分别为和.
根据题意,得,
解得,
则, ,.
则这种三色冰淇淋中咖啡色 红色和白色配料分别是,和.
【点睛】考查一元一次方程的应用,得到冰淇淋质量和的等量关系是解决本题的关键;注意有比的问题应设比中的每一份为x.
22.(1)胜1场得2分,负1场得1分
(2)某队的胜场总积分能等于它的负场总积分的2倍
(3)不能,详见解析
【分析】(1)利用东方队和光明队的数据设胜1场得分,则东方队负场总积分为分,可得负1场得分;光明队负场总积分为分,可得负1场得分,再建立方程求解即可;
(2)设一个队胜的场次为,则负的场次为,再根据胜场总积分能等于它的负场总积分的2倍,再列方程求解即可;
(3)设一个队胜的场次为,则负的场次为,再根据负场总积分能等于它的胜场总积分的2倍,再列方程求解即可.
【详解】(1)解:能.利用东方队和光明队的数据设胜1场得分,
则东方队负场总积分为分,
∴负1场得分;
光明队负场总积分为分,
∴负1场得分.
由此得方程,
解得.
则.
答:胜1场得2分,负1场得1分.
(2)能.设一个队胜的场次为,则负的场次为.
由题意,得,
解得.
所以某队的胜场总积分能等于它的负场总积分的2倍.
(3)不能.设一个队胜的场次为,则负的场次为.
由题意,得,
解得.
因为胜的场次不可能为分数,所以某队的负场总积分不能等于它的胜场总积分的2倍
【点睛】本题考查的是一元一次方程的应用,理解题意,准确的确定相等关系并列方程是解本题的关键.
23.5
【分析】从甲盒中拿出a个黑子放入乙盒,那么甲盒的棋子数为个,乙盒的棋子数为个,再根据乙盒棋子总数是甲盒所剩棋子数的2倍列出方程求解即可.
【详解】解:由题意得,,
解得,
∴a的值为5.
【点睛】本题主要考查了一元一次方程的实际应用,正确理解题意找到等量关系列出方程是解题的关键.
24.198里
【分析】设第六天走的路程为x里,则第五天走的路程为里,依次往前推,第一天走的路程为里,根据每天的路程加起来为378里,列方程即可解答.
【详解】解:设第六天走的路程为x里,则第五天走的路程为里,
依此往前推,第一天走的路程为里,
依题意,得:,
解得:,
,(里),
答:此人第一和第六这两天共走了198里.
【点睛】本题考查了一元一次方程的实际应用,正确地用未知数表示每一天走的路程是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
