6.1组合图形的面积暑假预习练(含解析)北师大版数学五年级上册
文档属性
| 名称 | 6.1组合图形的面积暑假预习练(含解析)北师大版数学五年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 338.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 16:34:40 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
6.1组合图形的面积
学校:___________姓名:___________班级:___________考号:___________
一、选择题
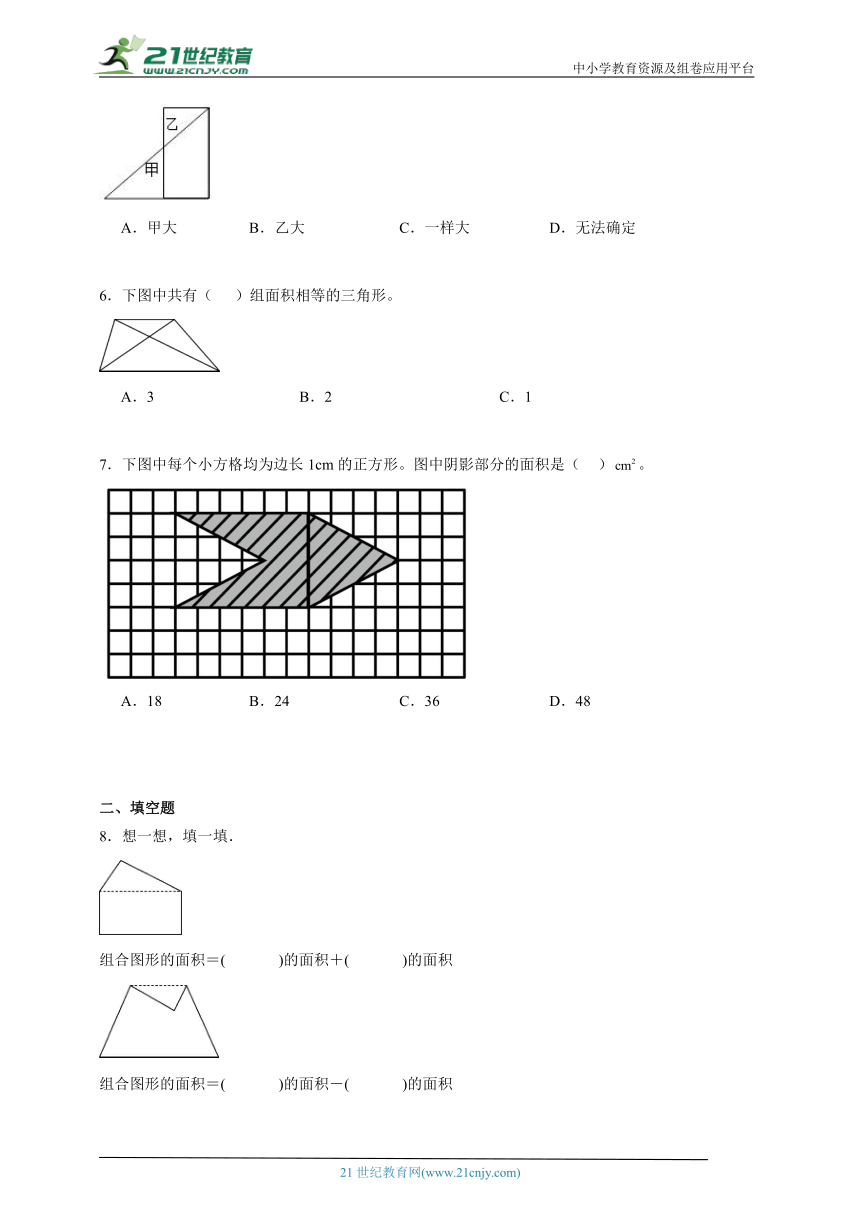
1.下图是由( )拼成的。
A.三角形和正方形 B.长方形和梯形 C.平行四边形和长方形
2.图中阴影部分的面积是( )平方厘米。
A.24 B.28 C.32
3.下面两个图形中的大、小正方形的面积分别相等,则甲涂色部分的面积与乙涂色部分的面积( )。
A.相等 B.甲大于乙 C.甲小于乙
4.要求下图的面积,可以把它分成已经学过的基本图形。下面的分法中,不正确的是( )。
A. B. C.
5.甲和乙的面积比较,结果( ).
A.甲大 B.乙大 C.一样大 D.无法确定
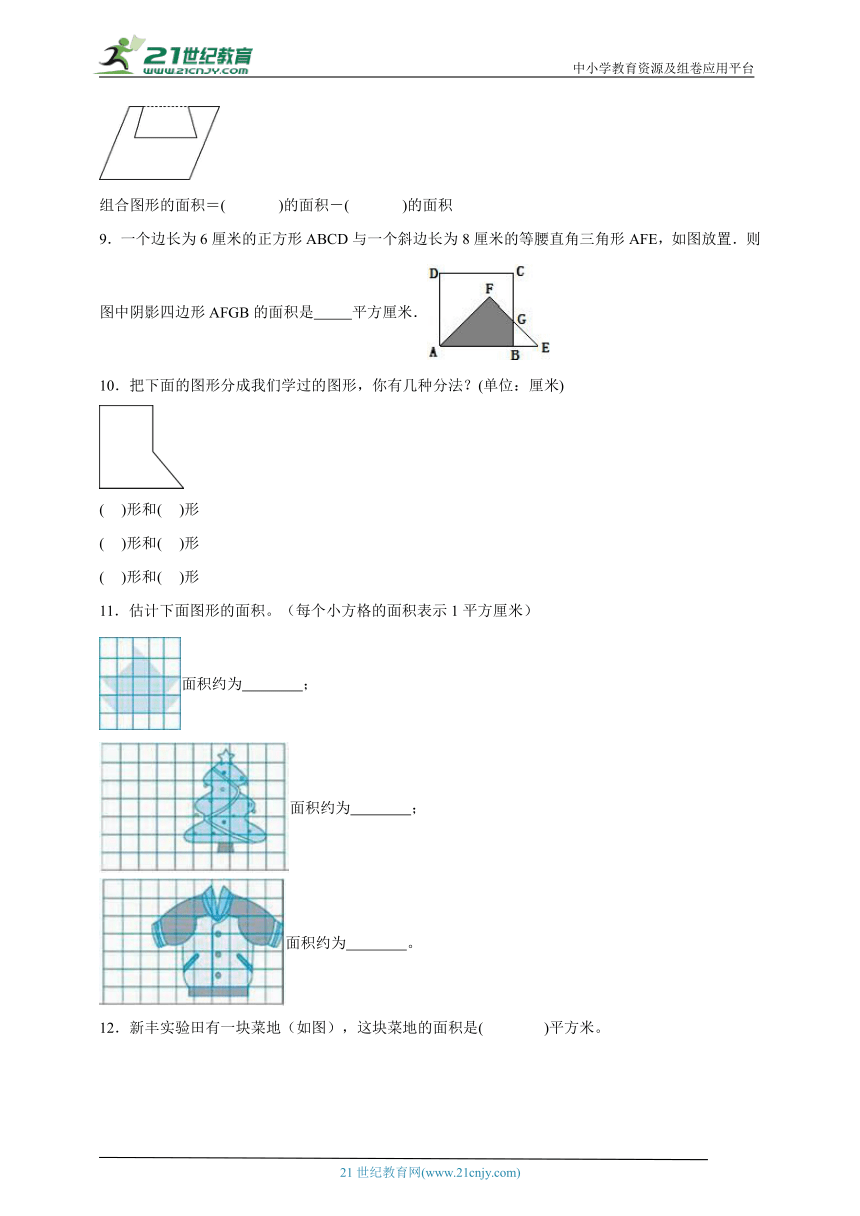
6.下图中共有( )组面积相等的三角形。
A.3 B.2 C.1
7.下图中每个小方格均为边长1cm的正方形。图中阴影部分的面积是( )。
A.18 B.24 C.36 D.48
二、填空题
8.想一想,填一填.
组合图形的面积=( )的面积+( )的面积
组合图形的面积=( )的面积-( )的面积
组合图形的面积=( )的面积-( )的面积
9.一个边长为6厘米的正方形ABCD与一个斜边长为8厘米的等腰直角三角形AFE,如图放置.则图中阴影四边形AFGB的面积是 平方厘米.
10.把下面的图形分成我们学过的图形,你有几种分法?(单位:厘米)
( )形和( )形
( )形和( )形
( )形和( )形
11.估计下面图形的面积。(每个小方格的面积表示1平方厘米)
面积约为 ;
面积约为 ;
面积约为 。
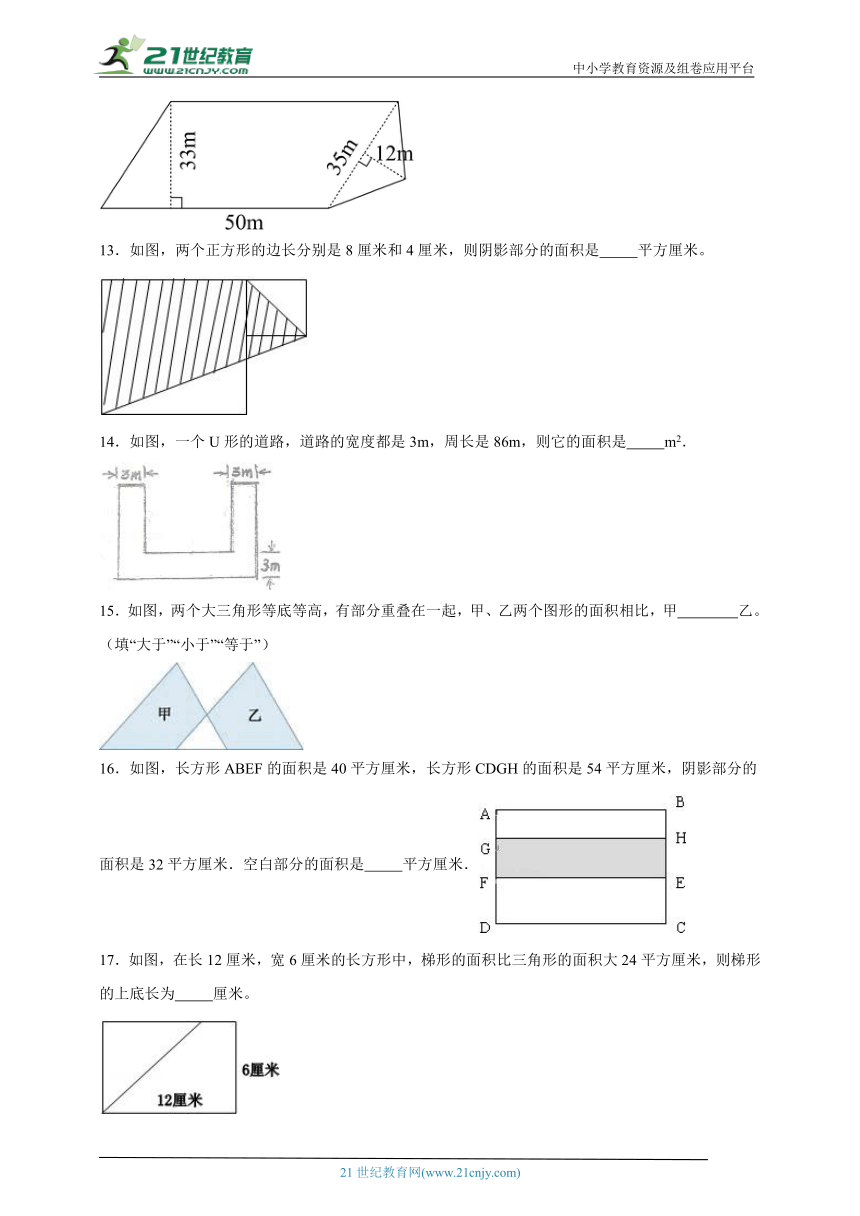
12.新丰实验田有一块菜地(如图),这块菜地的面积是( )平方米。
13.如图,两个正方形的边长分别是8厘米和4厘米,则阴影部分的面积是 平方厘米。
14.如图,一个U形的道路,道路的宽度都是3m,周长是86m,则它的面积是 m2.
15.如图,两个大三角形等底等高,有部分重叠在一起,甲、乙两个图形的面积相比,甲 乙。(填“大于”“小于”“等于”)
16.如图,长方形ABEF的面积是40平方厘米,长方形CDGH的面积是54平方厘米,阴影部分的面积是32平方厘米.空白部分的面积是 平方厘米.
17.如图,在长12厘米,宽6厘米的长方形中,梯形的面积比三角形的面积大24平方厘米,则梯形的上底长为 厘米。
三、判断题
18.计算组合图形的面积也要用到基本图形的面积公式。 ( )
19.只能分割成长方形和三角形.( )
20.两个完全相同的图形的面积一定相等;两个面积相等的图形的形状也一定相同。( )
四、计算题
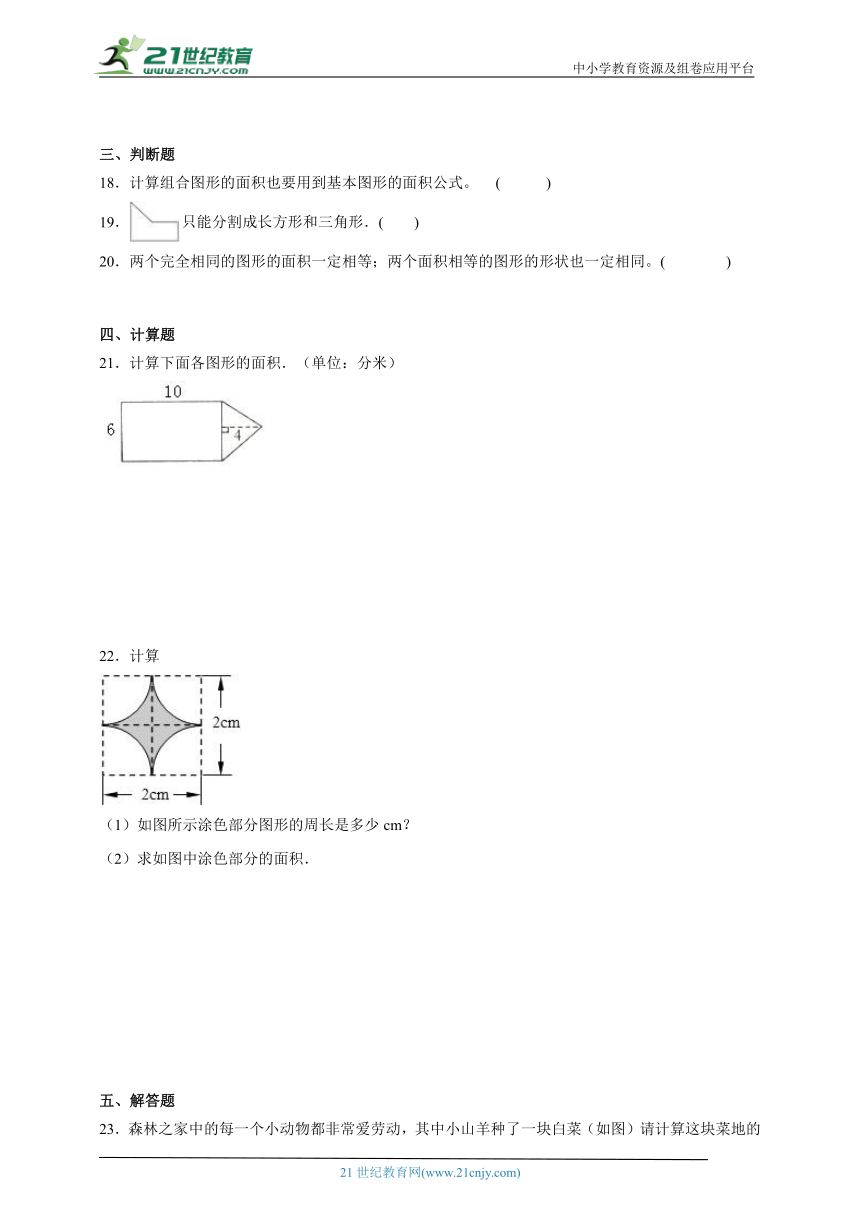
21.计算下面各图形的面积.(单位:分米)
22.计算
(1)如图所示涂色部分图形的周长是多少cm?
(2)求如图中涂色部分的面积.
五、解答题
23.森林之家中的每一个小动物都非常爱劳动,其中小山羊种了一块白菜(如图)请计算这块菜地的面积.
24.如图,有一个正方形花坛,在花坛周围铺3米宽的小路(阴影部分),已知小路的总面积是600平方米,求花坛占地多少。
25.小区计划在楼宇间再修建一块草坪,形状及数据如图。
(1)请你帮忙算一算,这块草坪的面积是多少平方米?
(2)如果每平方米草坪每天大约可以吸收0.02千克的二氧化碳,这块草坪建好后每天能吸收多少千克的二氧化碳?
26.把下面各个图形分成已学过的图形,并与同伴交流你的想法。
27.新丰小学有一块菜地,形状如下图,请你求出这块菜地的面积.
《6.1组合图形的面积》参考答案
题号 1 2 3 4 5 6 7
答案 B A A C D A B
1.B
【分析】观察图形,按照下图的所示连接,把图形分成一个上半部分是长方形,下半部分是梯形,据此解答。
【详解】根据分析可知,可分成一个长方形和梯形。
故答案选:B
【点睛】本题考查图形的分割,关键是正确识别图形,分割成熟知的图形进行解答。
2.A
【分析】观察图形可知,阴影部分是有两个边长为4厘米的正方形重叠形成的,由此可知,其阴影部分面积是由两个边长是4厘米正方形面积和减去两个边长为2厘米正方形面积和;根据正方形面积公式:边长×边长,代入数据,即可解答。
【详解】4×4×2-2×2×2
=16×2-4×2
=32-8
=24(平方厘米)
故答案选:A
【点睛】本题考查正方形面积公式的应用;关键是明确阴影部分面积需要减去两个小正方形面积。
3.A
【分析】由图可知,甲、乙两个涂色部分是三角形,三角形的面积=底×高÷2,分别表示出甲、乙两个涂色部分的面积,最后比较大小即可。
【详解】假设大正方形的边长为a,小正方形的边长为b。
甲涂色部分的面积:ab÷2=ab
乙涂色部分的面积:ab÷2=ab
因为ab=ab,所以甲涂色部分的面积=乙涂色部分的面积。
故答案为:A
【点睛】甲三角形的底等于乙三角形的高,甲三角形的高等于乙三角形的底,所以甲和乙的面积相等。
4.C
【分析】计算组合图形的面积,要根据已知条件对图形进行分割,转化成已学过的简单图形,先分别计算出它们的面积,再求和或差。
【详解】
A.通过添加辅助线,把分割成一个梯形和一个长方形,可根据梯形、长方形面积计算公式,分别求出梯形、长方形的面积,再把它们的面积加起来。A选项正确。
B.通过添加辅助线,把分割成一个梯形和一个长方形,可根据梯形、长方形面积计算公式,分别求出梯形、长方形的面积,再把它们的面积加起来。B选项正确。
C.通过添加辅助线,把分割成一个不规则的四边形和一个三角形,不规则四边形的面积不能利用公式求出来。C选项错误。
故答案为:C
【点睛】在对组合图形进行分割时,一定要考虑到分割出来的图形是已学过的简单图形。
5.D
【分析】根据三角形面积公式S=ah÷2和长方形面积公式S=ah可知高和长相等的三角形面积与长方形面积无法确定,再根据等量关系可知甲和乙的面积之间的关系.
【详解】由三角形面积公式S=ah÷2和长方形面积公式S=ah可知高和长相等的三角形面积与长方形面积无法确定, 甲的面积=三角形面积﹣①的面积;乙的面积=长方形面积﹣①的面积;则甲的面积和乙的面积无法确定大小.
故选D.
6.A
【分析】
如图,由图可知,①和②两个三角形分别加上顶部的③三角形后组成两个新的三角形,根据两条平行线之间的距离处处相等,可知这两个新三角形是等底等高的,面积相等,所以①和②两个三角形的面积也是相等的,同理,①和②两个三角形分别加上底边的④三角形后组成两个新的三角形,这两个三角形也是等底等高的,面积相等,据此解答。
【详解】如图:
因为①+③=②+③
①+④=②+④
所以①=②
共有3组面积相等的三角形。
故答案为:A
【点睛】此题考查的目的是理解掌握等底等高的三角形的面积相等。
7.B
【分析】根据图形的特点,可以通过平移,把右边的三角形向左平移6格,拼成一个长是6cm,宽是4cm的长方形,根据长方形的面积公式:S=ab,把数据代入公式解答。
【详解】6×4=24()
下图中每个小方格均为边长1cm的正方形。图中阴影部分的面积是24cm2。
故答案为:B
【点睛】此题主要考查平移和长方形面积公式的灵活运用。
8. 三角形 长方形 梯形 三角形 平行四边形 梯形
【解析】略
9.14
【分析】由图意可知:BE=BG=8﹣6=2厘米,又因阴影部分的面积=三角形AEF的面积﹣三角形GBE的面积,利用三角形的面积公式即可求解.
【详解】解:因为BE=BG=8﹣6=2厘米,
则阴影部分的面积为:
8×(8÷2)÷2﹣(8﹣6)×(8﹣6)÷2,
=16﹣2,
=14(平方厘米);
答:图中阴影四边形AFGB的面积是14平方厘米.
【点睛】得出三角形GBE是等腰直角三角形,且求出其直角边的长度,问题即可得解.
10.长方 梯 梯 三角 长方 三角
【详解】略
11. 11平方厘米 13平方厘米 30平方厘米
【分析】根据题意,
(1)图1可以先数整格数再加上7个半格即可。
(2)图2先数整格数再加上14个半格即可。
(3)图3先数整格数再加上26个半格即可。
【详解】(1)第一个图形,整格的有7个,面积是7平方厘米,半格的有7个,约是4平方厘米,总面积约是7+4=11(平方厘米)
(2)第二个图形,整格的有6个,面积是6平方厘米,半格的有14个,约是7平方厘米。总面积约是6+7=13(平方厘米)。
(3)第三个图形,整格的有17个,面积是17平方厘米,半格的有26个,约是13平方厘米,总面积约是17+13=30(平方厘米)。
【点睛】解答此题,要注意认真分析图形,可以将所给的图形分割成我们常见的图形,弄清图形所占的方格数,然后再计算图形的面积即可。
12.1860
【分析】菜地的面积=平行四边形面积+三角形面积,平行四边形面积=底×高,三角形面积=底×高÷2,据此列式计算。
【详解】50×33+35×12÷2
=1650+210
=1860(平方米)
这块菜地的面积是1860平方米。
13.64
【详解】阴影部分的面积等于梯形ABCD的面积减去一个三角形AED的面积,如图:
(8+4)×(8+4)÷2﹣4×4÷2
=12×12÷2﹣8
=72﹣8
=64(平方厘米)
阴影部分的面积是64平方厘米.
14.120
【详解】试题分析:由题意可得:将这个图形“捋直”,则变成了一个宽为3米的长方形,且这个长方形的周长已知,于是可以求出其长,进而利用长方形的面积公式即可求解.
解:86÷2﹣3,
=43﹣3,
=40(米),
40×3=120(平方米);
答:这个道路的面积是120平方米.
故答案为120.
点评:解答此题的关键是:将道路变形为宽为3米的长方形,问题即可轻松得解.
15.等于
【分析】根据三角形的面积公式,结合题意,解题即可。
【详解】两个三角形等底等高,面积相等,同时减去重叠的部分后剩下的面积也相等,所以甲的面积等于乙的面积。
【点睛】本题考查了三角形的面积,灵活运用三角形的面积公式是解题的关键。
16.30
【详解】试题分析:由题意可知:两个长方形的面积分别减去阴影部分的面积,再将差加在一起即可得解;或者将两个长方形的面积加在一起,再减去2个阴影部分的面积(重合部分),即可得解.
解:40﹣32+(54﹣32),
=8+22,
=30(平方厘米),
或者40+54﹣32﹣32,
=94﹣64,
=30(平方厘米).
答:空白部分的面积是30平方厘米.
故答案为30.
点评:解答此题的关键是明白:阴影部分是两个长方形的公共部分.
17.4
【分析】先依据长方形的面积公式求出长方形的面积,进而依据三角形的面积和梯形的面积的关系即可求出梯形的面积,进而依据梯形的面积公式即可求出梯形的上底。
【详解】12×6=72(平方厘米),
解:设三角形的面积为x,则梯形的面积为(24+x),
x+24+x=72,
2x=48,
x=24,
24×2=48(平方厘米);
48×2÷6﹣12,
=96÷6﹣12,
=16﹣12,
=4(厘米);
梯形的上底长为4厘米。
【点睛】此题主要考查长方形和梯形的面积的计算方法的灵活应用。
18.√
【分析】在计算组合图形的面积,一般通过分割法或添补的方法,把它转化成基本图形后进行计算。
【详解】在计算组合图形的面积,把它转化成基本图形后进行计算,所以也要用到基本图形的面积公式。原题说法正确。
故答案为:√
【点睛】本题考查了解决组合图形的面积时的基本方法,平时计算时多注意观察,即可判断。
19.×
【详解】略
20.×
【分析】假设两个图形都是三角形,两个完全相同的图形,说明它们底和高都是相等的,根据三角形的面积S=ah,面积一定相等;如果两个三角形的面积相等,只能说明底和高的乘积相等,底和高的长度不一定相等,据此判断即可。
【详解】由分析可知,两个完全相同的图形的面积一定相等;两个面积相等的图形的形状也一定相同;说法错误。
故答案为:×
【点睛】此题主要考查三角形的面积公式的灵活应用。
21.6×10+6×4÷2=72(平方分米)
【详解】长方形的面积=长×宽,三角形的面积=底×高÷2.
22.(1)周长是6.28厘米 (2)涂色部分的面积是0.86平方厘米
【详解】(1)解:2÷2=1(厘米) 3.14×1×2=6.28(厘米);
答:这个涂色部分的周长是6.28厘米
(2)解:2×2﹣3.14×12 ,
=4﹣3.14,
=0.86(平方厘米);
答:涂色部分的面积是0.86平方厘米
23.146平方米
【详解】试题分析:如图所示,可以将菜地分割成两个长方形,分别求出两个长方形的长和宽,再利用长方形的面积公式即可求解.
解:8×7+18×5,
=56+90,
=146(平方米);
答:这块菜地的面积146平方米.
点评:此题主要考查长方形的面积的计算方法,关键是弄清楚两个长方形的长和宽的值.
24.2209平方米
【分析】
如图,把小路分成4个完全相同的长方形,其中长方形的宽是3米,先用除法求出一个长方形的面积,再除以宽,就是长方形的长,长方形的长-小路宽=花坛的边长,根据正方形的面积=边长×边长,计算即可。
【详解】600÷4=150(平方米)
150÷3-3
=50-3
=47(米)
47×47=2209(平方米)
答:花坛占地2209平方米。
【点睛】此题考查了有关长方形、正方形的面积计算,适当的分割,先求出正方形的边长是解题关键。
25.(1)33平方米;
(2)0.66千克
【分析】(1)将草坪分割如下:
则草坪面积等于两个小长方形的面积,将数据代入长方形面积公式:S=ab计算即可;
(2)用草坪面积×每平方米草坪每天大约可以吸收二氧化碳的质量即可。
【详解】(1)7×3+4×(6-3)
=21+4×3
=21+12
=33(平方米)
答:这块草坪的面积是33平方米。
(2)33×0.02=0.66(千克)
答:这块草坪建好后每天能吸收0.66千克的二氧化碳。
【点睛】本题主要考查求组合图形的面积。
26.第一个图形分成一个长方形和一个梯形;第二个图形分成三个长方形。
【分析】根据长方形、梯形的特征,把两个图形分成已学过的图形,第一个图形可以分成一个长方形和一个梯形,第二个图形可以分成三个长方形。答案不唯一,合理即可。
【详解】如图:
答:第一个图形分成一个长方形和一个梯形;第二个图形分成三个长方形即可。答案不唯一,合理即可。
27.2250m2
【详解】60×34+35×12÷2=2250(m2)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.1组合图形的面积
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下图是由( )拼成的。
A.三角形和正方形 B.长方形和梯形 C.平行四边形和长方形
2.图中阴影部分的面积是( )平方厘米。
A.24 B.28 C.32
3.下面两个图形中的大、小正方形的面积分别相等,则甲涂色部分的面积与乙涂色部分的面积( )。
A.相等 B.甲大于乙 C.甲小于乙
4.要求下图的面积,可以把它分成已经学过的基本图形。下面的分法中,不正确的是( )。
A. B. C.
5.甲和乙的面积比较,结果( ).
A.甲大 B.乙大 C.一样大 D.无法确定
6.下图中共有( )组面积相等的三角形。
A.3 B.2 C.1
7.下图中每个小方格均为边长1cm的正方形。图中阴影部分的面积是( )。
A.18 B.24 C.36 D.48
二、填空题
8.想一想,填一填.
组合图形的面积=( )的面积+( )的面积
组合图形的面积=( )的面积-( )的面积
组合图形的面积=( )的面积-( )的面积
9.一个边长为6厘米的正方形ABCD与一个斜边长为8厘米的等腰直角三角形AFE,如图放置.则图中阴影四边形AFGB的面积是 平方厘米.
10.把下面的图形分成我们学过的图形,你有几种分法?(单位:厘米)
( )形和( )形
( )形和( )形
( )形和( )形
11.估计下面图形的面积。(每个小方格的面积表示1平方厘米)
面积约为 ;
面积约为 ;
面积约为 。
12.新丰实验田有一块菜地(如图),这块菜地的面积是( )平方米。
13.如图,两个正方形的边长分别是8厘米和4厘米,则阴影部分的面积是 平方厘米。
14.如图,一个U形的道路,道路的宽度都是3m,周长是86m,则它的面积是 m2.
15.如图,两个大三角形等底等高,有部分重叠在一起,甲、乙两个图形的面积相比,甲 乙。(填“大于”“小于”“等于”)
16.如图,长方形ABEF的面积是40平方厘米,长方形CDGH的面积是54平方厘米,阴影部分的面积是32平方厘米.空白部分的面积是 平方厘米.
17.如图,在长12厘米,宽6厘米的长方形中,梯形的面积比三角形的面积大24平方厘米,则梯形的上底长为 厘米。
三、判断题
18.计算组合图形的面积也要用到基本图形的面积公式。 ( )
19.只能分割成长方形和三角形.( )
20.两个完全相同的图形的面积一定相等;两个面积相等的图形的形状也一定相同。( )
四、计算题
21.计算下面各图形的面积.(单位:分米)
22.计算
(1)如图所示涂色部分图形的周长是多少cm?
(2)求如图中涂色部分的面积.
五、解答题
23.森林之家中的每一个小动物都非常爱劳动,其中小山羊种了一块白菜(如图)请计算这块菜地的面积.
24.如图,有一个正方形花坛,在花坛周围铺3米宽的小路(阴影部分),已知小路的总面积是600平方米,求花坛占地多少。
25.小区计划在楼宇间再修建一块草坪,形状及数据如图。
(1)请你帮忙算一算,这块草坪的面积是多少平方米?
(2)如果每平方米草坪每天大约可以吸收0.02千克的二氧化碳,这块草坪建好后每天能吸收多少千克的二氧化碳?
26.把下面各个图形分成已学过的图形,并与同伴交流你的想法。
27.新丰小学有一块菜地,形状如下图,请你求出这块菜地的面积.
《6.1组合图形的面积》参考答案
题号 1 2 3 4 5 6 7
答案 B A A C D A B
1.B
【分析】观察图形,按照下图的所示连接,把图形分成一个上半部分是长方形,下半部分是梯形,据此解答。
【详解】根据分析可知,可分成一个长方形和梯形。
故答案选:B
【点睛】本题考查图形的分割,关键是正确识别图形,分割成熟知的图形进行解答。
2.A
【分析】观察图形可知,阴影部分是有两个边长为4厘米的正方形重叠形成的,由此可知,其阴影部分面积是由两个边长是4厘米正方形面积和减去两个边长为2厘米正方形面积和;根据正方形面积公式:边长×边长,代入数据,即可解答。
【详解】4×4×2-2×2×2
=16×2-4×2
=32-8
=24(平方厘米)
故答案选:A
【点睛】本题考查正方形面积公式的应用;关键是明确阴影部分面积需要减去两个小正方形面积。
3.A
【分析】由图可知,甲、乙两个涂色部分是三角形,三角形的面积=底×高÷2,分别表示出甲、乙两个涂色部分的面积,最后比较大小即可。
【详解】假设大正方形的边长为a,小正方形的边长为b。
甲涂色部分的面积:ab÷2=ab
乙涂色部分的面积:ab÷2=ab
因为ab=ab,所以甲涂色部分的面积=乙涂色部分的面积。
故答案为:A
【点睛】甲三角形的底等于乙三角形的高,甲三角形的高等于乙三角形的底,所以甲和乙的面积相等。
4.C
【分析】计算组合图形的面积,要根据已知条件对图形进行分割,转化成已学过的简单图形,先分别计算出它们的面积,再求和或差。
【详解】
A.通过添加辅助线,把分割成一个梯形和一个长方形,可根据梯形、长方形面积计算公式,分别求出梯形、长方形的面积,再把它们的面积加起来。A选项正确。
B.通过添加辅助线,把分割成一个梯形和一个长方形,可根据梯形、长方形面积计算公式,分别求出梯形、长方形的面积,再把它们的面积加起来。B选项正确。
C.通过添加辅助线,把分割成一个不规则的四边形和一个三角形,不规则四边形的面积不能利用公式求出来。C选项错误。
故答案为:C
【点睛】在对组合图形进行分割时,一定要考虑到分割出来的图形是已学过的简单图形。
5.D
【分析】根据三角形面积公式S=ah÷2和长方形面积公式S=ah可知高和长相等的三角形面积与长方形面积无法确定,再根据等量关系可知甲和乙的面积之间的关系.
【详解】由三角形面积公式S=ah÷2和长方形面积公式S=ah可知高和长相等的三角形面积与长方形面积无法确定, 甲的面积=三角形面积﹣①的面积;乙的面积=长方形面积﹣①的面积;则甲的面积和乙的面积无法确定大小.
故选D.
6.A
【分析】
如图,由图可知,①和②两个三角形分别加上顶部的③三角形后组成两个新的三角形,根据两条平行线之间的距离处处相等,可知这两个新三角形是等底等高的,面积相等,所以①和②两个三角形的面积也是相等的,同理,①和②两个三角形分别加上底边的④三角形后组成两个新的三角形,这两个三角形也是等底等高的,面积相等,据此解答。
【详解】如图:
因为①+③=②+③
①+④=②+④
所以①=②
共有3组面积相等的三角形。
故答案为:A
【点睛】此题考查的目的是理解掌握等底等高的三角形的面积相等。
7.B
【分析】根据图形的特点,可以通过平移,把右边的三角形向左平移6格,拼成一个长是6cm,宽是4cm的长方形,根据长方形的面积公式:S=ab,把数据代入公式解答。
【详解】6×4=24()
下图中每个小方格均为边长1cm的正方形。图中阴影部分的面积是24cm2。
故答案为:B
【点睛】此题主要考查平移和长方形面积公式的灵活运用。
8. 三角形 长方形 梯形 三角形 平行四边形 梯形
【解析】略
9.14
【分析】由图意可知:BE=BG=8﹣6=2厘米,又因阴影部分的面积=三角形AEF的面积﹣三角形GBE的面积,利用三角形的面积公式即可求解.
【详解】解:因为BE=BG=8﹣6=2厘米,
则阴影部分的面积为:
8×(8÷2)÷2﹣(8﹣6)×(8﹣6)÷2,
=16﹣2,
=14(平方厘米);
答:图中阴影四边形AFGB的面积是14平方厘米.
【点睛】得出三角形GBE是等腰直角三角形,且求出其直角边的长度,问题即可得解.
10.长方 梯 梯 三角 长方 三角
【详解】略
11. 11平方厘米 13平方厘米 30平方厘米
【分析】根据题意,
(1)图1可以先数整格数再加上7个半格即可。
(2)图2先数整格数再加上14个半格即可。
(3)图3先数整格数再加上26个半格即可。
【详解】(1)第一个图形,整格的有7个,面积是7平方厘米,半格的有7个,约是4平方厘米,总面积约是7+4=11(平方厘米)
(2)第二个图形,整格的有6个,面积是6平方厘米,半格的有14个,约是7平方厘米。总面积约是6+7=13(平方厘米)。
(3)第三个图形,整格的有17个,面积是17平方厘米,半格的有26个,约是13平方厘米,总面积约是17+13=30(平方厘米)。
【点睛】解答此题,要注意认真分析图形,可以将所给的图形分割成我们常见的图形,弄清图形所占的方格数,然后再计算图形的面积即可。
12.1860
【分析】菜地的面积=平行四边形面积+三角形面积,平行四边形面积=底×高,三角形面积=底×高÷2,据此列式计算。
【详解】50×33+35×12÷2
=1650+210
=1860(平方米)
这块菜地的面积是1860平方米。
13.64
【详解】阴影部分的面积等于梯形ABCD的面积减去一个三角形AED的面积,如图:
(8+4)×(8+4)÷2﹣4×4÷2
=12×12÷2﹣8
=72﹣8
=64(平方厘米)
阴影部分的面积是64平方厘米.
14.120
【详解】试题分析:由题意可得:将这个图形“捋直”,则变成了一个宽为3米的长方形,且这个长方形的周长已知,于是可以求出其长,进而利用长方形的面积公式即可求解.
解:86÷2﹣3,
=43﹣3,
=40(米),
40×3=120(平方米);
答:这个道路的面积是120平方米.
故答案为120.
点评:解答此题的关键是:将道路变形为宽为3米的长方形,问题即可轻松得解.
15.等于
【分析】根据三角形的面积公式,结合题意,解题即可。
【详解】两个三角形等底等高,面积相等,同时减去重叠的部分后剩下的面积也相等,所以甲的面积等于乙的面积。
【点睛】本题考查了三角形的面积,灵活运用三角形的面积公式是解题的关键。
16.30
【详解】试题分析:由题意可知:两个长方形的面积分别减去阴影部分的面积,再将差加在一起即可得解;或者将两个长方形的面积加在一起,再减去2个阴影部分的面积(重合部分),即可得解.
解:40﹣32+(54﹣32),
=8+22,
=30(平方厘米),
或者40+54﹣32﹣32,
=94﹣64,
=30(平方厘米).
答:空白部分的面积是30平方厘米.
故答案为30.
点评:解答此题的关键是明白:阴影部分是两个长方形的公共部分.
17.4
【分析】先依据长方形的面积公式求出长方形的面积,进而依据三角形的面积和梯形的面积的关系即可求出梯形的面积,进而依据梯形的面积公式即可求出梯形的上底。
【详解】12×6=72(平方厘米),
解:设三角形的面积为x,则梯形的面积为(24+x),
x+24+x=72,
2x=48,
x=24,
24×2=48(平方厘米);
48×2÷6﹣12,
=96÷6﹣12,
=16﹣12,
=4(厘米);
梯形的上底长为4厘米。
【点睛】此题主要考查长方形和梯形的面积的计算方法的灵活应用。
18.√
【分析】在计算组合图形的面积,一般通过分割法或添补的方法,把它转化成基本图形后进行计算。
【详解】在计算组合图形的面积,把它转化成基本图形后进行计算,所以也要用到基本图形的面积公式。原题说法正确。
故答案为:√
【点睛】本题考查了解决组合图形的面积时的基本方法,平时计算时多注意观察,即可判断。
19.×
【详解】略
20.×
【分析】假设两个图形都是三角形,两个完全相同的图形,说明它们底和高都是相等的,根据三角形的面积S=ah,面积一定相等;如果两个三角形的面积相等,只能说明底和高的乘积相等,底和高的长度不一定相等,据此判断即可。
【详解】由分析可知,两个完全相同的图形的面积一定相等;两个面积相等的图形的形状也一定相同;说法错误。
故答案为:×
【点睛】此题主要考查三角形的面积公式的灵活应用。
21.6×10+6×4÷2=72(平方分米)
【详解】长方形的面积=长×宽,三角形的面积=底×高÷2.
22.(1)周长是6.28厘米 (2)涂色部分的面积是0.86平方厘米
【详解】(1)解:2÷2=1(厘米) 3.14×1×2=6.28(厘米);
答:这个涂色部分的周长是6.28厘米
(2)解:2×2﹣3.14×12 ,
=4﹣3.14,
=0.86(平方厘米);
答:涂色部分的面积是0.86平方厘米
23.146平方米
【详解】试题分析:如图所示,可以将菜地分割成两个长方形,分别求出两个长方形的长和宽,再利用长方形的面积公式即可求解.
解:8×7+18×5,
=56+90,
=146(平方米);
答:这块菜地的面积146平方米.
点评:此题主要考查长方形的面积的计算方法,关键是弄清楚两个长方形的长和宽的值.
24.2209平方米
【分析】
如图,把小路分成4个完全相同的长方形,其中长方形的宽是3米,先用除法求出一个长方形的面积,再除以宽,就是长方形的长,长方形的长-小路宽=花坛的边长,根据正方形的面积=边长×边长,计算即可。
【详解】600÷4=150(平方米)
150÷3-3
=50-3
=47(米)
47×47=2209(平方米)
答:花坛占地2209平方米。
【点睛】此题考查了有关长方形、正方形的面积计算,适当的分割,先求出正方形的边长是解题关键。
25.(1)33平方米;
(2)0.66千克
【分析】(1)将草坪分割如下:
则草坪面积等于两个小长方形的面积,将数据代入长方形面积公式:S=ab计算即可;
(2)用草坪面积×每平方米草坪每天大约可以吸收二氧化碳的质量即可。
【详解】(1)7×3+4×(6-3)
=21+4×3
=21+12
=33(平方米)
答:这块草坪的面积是33平方米。
(2)33×0.02=0.66(千克)
答:这块草坪建好后每天能吸收0.66千克的二氧化碳。
【点睛】本题主要考查求组合图形的面积。
26.第一个图形分成一个长方形和一个梯形;第二个图形分成三个长方形。
【分析】根据长方形、梯形的特征,把两个图形分成已学过的图形,第一个图形可以分成一个长方形和一个梯形,第二个图形可以分成三个长方形。答案不唯一,合理即可。
【详解】如图:
答:第一个图形分成一个长方形和一个梯形;第二个图形分成三个长方形即可。答案不唯一,合理即可。
27.2250m2
【详解】60×34+35×12÷2=2250(m2)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
