2.1用字母表示数暑假预习练(含解析) 北京版数学七年级上册
文档属性
| 名称 | 2.1用字母表示数暑假预习练(含解析) 北京版数学七年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 691.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-09 11:36:53 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2.1用字母表示数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列选项中,能用表示的是( ).
A.整条线段的长度: B.整条线段的长度:
C.这个长方形的周长: D.这个图形的面积:
2.如果,那么代数式的值是( )
A.0 B.5 C.7 D.9
3.当时,的值是( )
A.5 B.13 C.21 D.25
4.已知每个人做某项工作的效率相同,个人做d天可以完成,若增加人,则完成工作所需的天数为( ).
A. B. C. D.
5.若三角形的一条边长为,这条边上的高为,则这个三角形的面积可以表示为( )
A. B. C. D.
6.某数的平方的5倍与1的差的一半,用代数式表示是( )
A. B. C. D.
7.甲袋有a千克大米,乙袋有b千克大米,如果从甲袋拿出9千克大米放入乙袋,那么甲、乙两袋质量相等.列成等式是( ).
A. B. C. D.
8.如图,是由正方形和相同大小的圆按照一定规律摆放而成,按此规律,则第10个图形中圆的个数是( )
A.40 B.41 C.31 D.19
9.在,,,,,,,中,代数式有( )
A.个 B.个 C.个 D.个
10.下列各式不是代数式的是( )
A.16 B. C. D.
11.当x=1时,代数式的值是2022,则当x=﹣1时,代数式的值是( )
A.2021 B.﹣2022 C.﹣2021 D.2022
12.某企业今年一月份投入新产品的研发资金为a万元,以后每月投入新产品的研发资金与上月相比增长率都是20%.该厂今年三月份投入新产品的研发资金为b万元,则( )
A. B. C. D.
二、填空题
13.一种商品每件盈利为a元,售出60件,共盈利 元(用含a的式子表示)
14.一个两位数,个位数字是x,十位数字是y,若个位数字与十位数字对调,则所得的新的两位数是 .
15.当x分别等于1和时,代数式的两个值 .(填“相等”“互为相反数”或“互为倒数”)
16.若代数式的值是5,则代数式 .
17.当时,代数式的值是 .
三、解答题
18.如图是一幢公寓窗户的形状,其上部是半圆形,下部是边长相同的四个小正方形,已知下部的小正方形的边长为,计算:
(1)窗户的总面积是多少?(窗框面积忽略不计)
(2)窗户内外框的总长是多少?
(3)如果窗户上安装的是玻璃,购买玻璃的费用是40元/,购买窗框的费用是24元/,当时,制作一扇窗户需要的费用是多少元?(取).
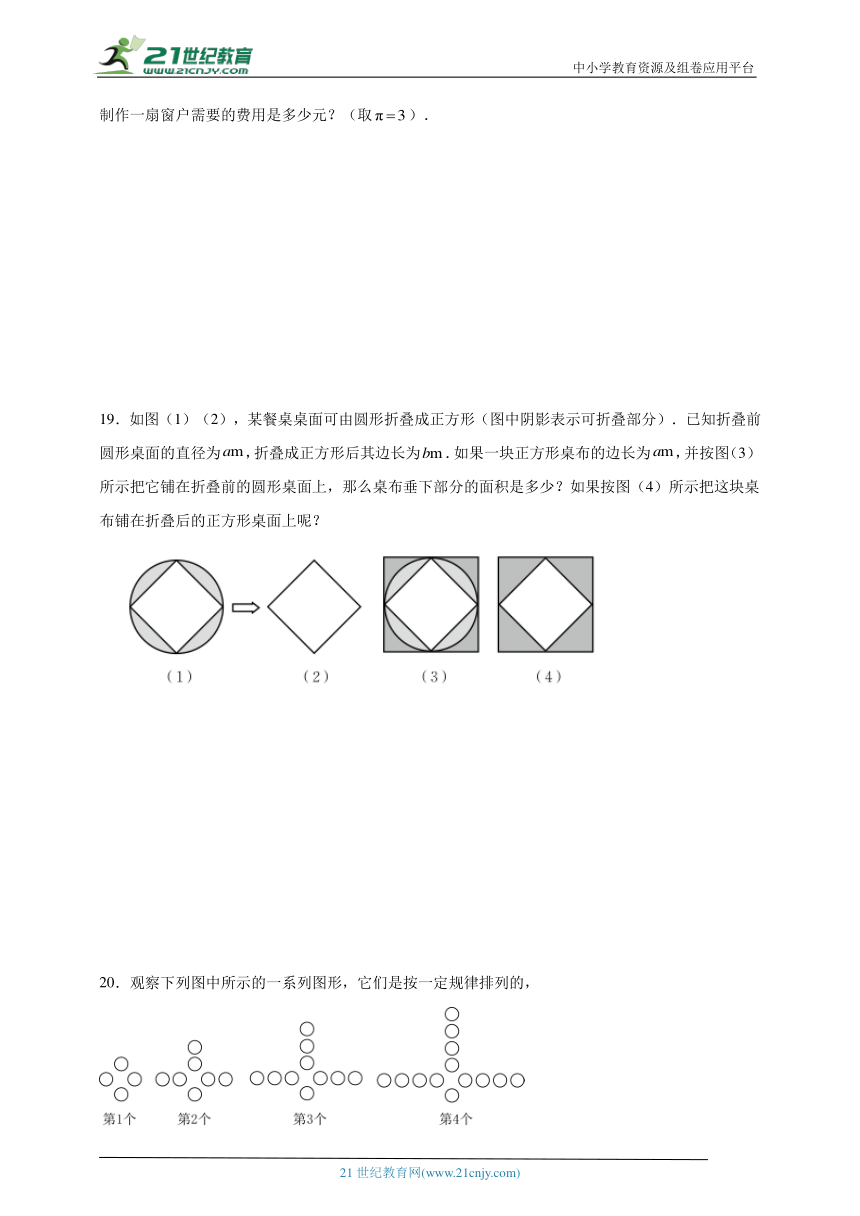
19.如图(1)(2),某餐桌桌面可由圆形折叠成正方形(图中阴影表示可折叠部分).已知折叠前圆形桌面的直径为,折叠成正方形后其边长为.如果一块正方形桌布的边长为,并按图(3)所示把它铺在折叠前的圆形桌面上,那么桌布垂下部分的面积是多少?如果按图(4)所示把这块桌布铺在折叠后的正方形桌面上呢?
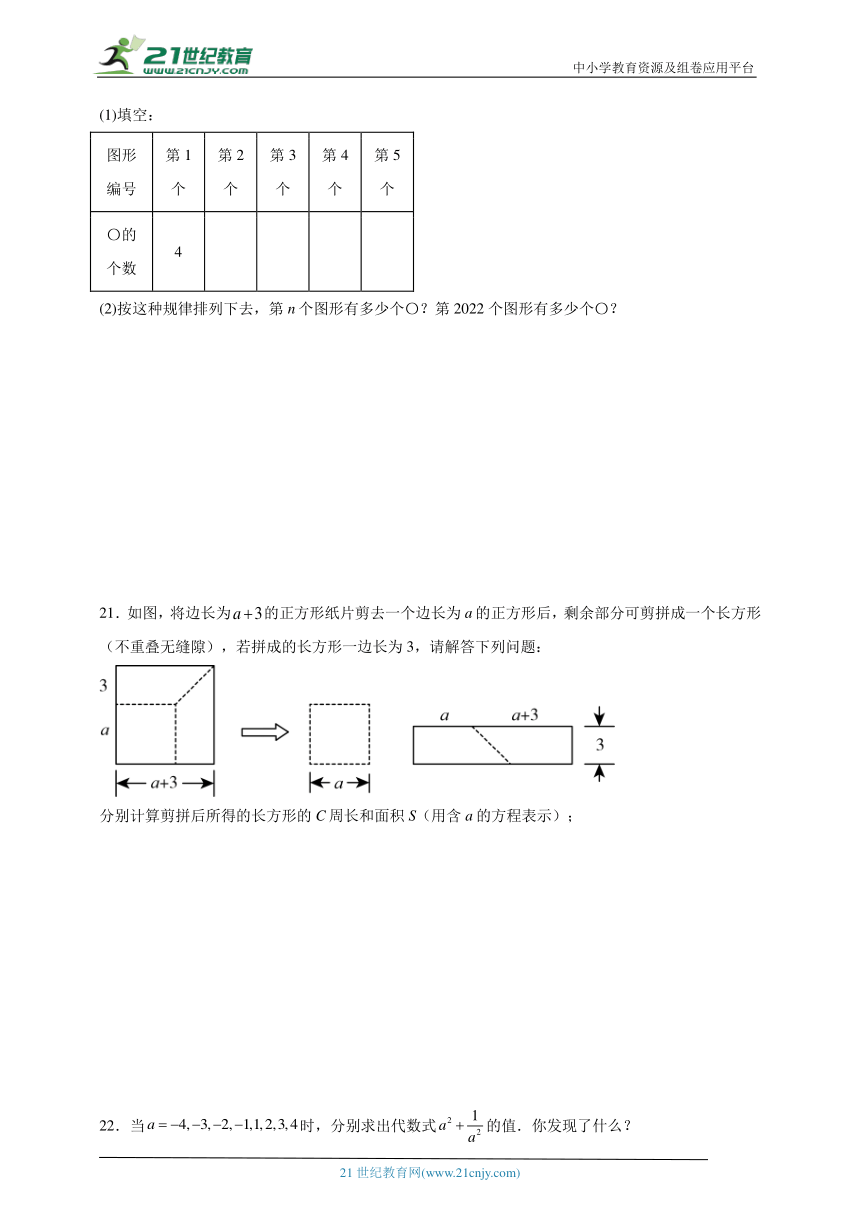
20.观察下列图中所示的一系列图形,它们是按一定规律排列的,
(1)填空:
图形编号 第1个 第2个 第3个 第4个 第5个
〇的个数 4
(2)按这种规律排列下去,第n个图形有多少个〇?第2022个图形有多少个〇?
21.如图,将边长为的正方形纸片剪去一个边长为a的正方形后,剩余部分可剪拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为3,请解答下列问题:
分别计算剪拼后所得的长方形的C周长和面积S(用含a的方程表示);
22.当时,分别求出代数式的值.你发现了什么?
23.回答下列问题:
(1)小明每季度有零花钱a元,拿出b元捐给爱心基金,平均每月剩余的零花钱是多少?
(2)七年级(1)班共有a名学生,其中有b名男生,男生的三分之一去参加篮球比赛了,班级剩余多少人?
(3)某种汽车油箱装满后有油,每小时耗油,行驶了,油箱剩余油量是多少?
(4)某商品原价每件a元,商场打折,现价每件b元,现买3件可以省多少元?
24.用同样大小的两种不同颜色的正方形纸片,按下图方式拼正方形.
第(1)个图形中有1个正方形;
第(2)个图形有1+3=4个小正方形;
第(3)个图形有1+3+5=9个小正方形;
第(4)个图形有1+3+5+7=16小正方形;
……
(1)根据上面的发现我们可以猜想:1+3+5+7+…+(2n﹣1)=______(用含n的代数式表示);
(2)请根据你的发现计算:
①1+3+5+7+…+99;
②101+103+105+…+199.
《2.1用字母表示数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D D D D B C A C
题号 11 12
答案 B D
1.C
【分析】本题考查了列代数式,解题的关键是掌握线段的长度和图形的周长、面积计算方法.分别计算各选项的结果,化简即可判断.
【详解】解:A、整条线段的长度为,故A不合题意;
B、整条线段的长度为,故B不合题意;
C、这个长方形的周长为,故C符合题意;
D、这个图形的面积为,故D不合题意.
故选:C.
2.D
【分析】本题考查了代数式求值:将代入,进行计算即可.
【详解】解:∵,
∴,
故选:D.
3.D
【分析】将代入原式,即可解答.
【详解】解:当时,
原式.
故选:D.
【点睛】本题考查了代入代数式的代入求值,熟练计算是解题的关键.
4.D
【分析】本题考查了用字母表示数,设每个人做某项工作的效率为1,则这项工作总量为,若增加r人,现在总人数是人,用工作总量除以总人数,即可求出完成工作所需的天数.
【详解】解:设每个人做某项工作的效率为1,则这项工作总量为,若增加r人,
则完成工作所需的天数为,
故选:D.
5.D
【分析】根据三角形面积公式即可求解.
【详解】解:三角形的面积=底高
故选:D.
【点睛】本题考查了用字母表示数,解题关键是理解题意正确列出代数式.
6.D
【分析】本题考查了列代数式.数的平方为,的5倍是,再表示与1的差,最后表示出差的一半,即可.
【详解】解:某数的平方的5倍与1的差的一半,用代数式表示是.
故选:D.
7.B
【分析】根据题意,找出数量关系,即可而出等式.
【详解】解:根据题意可得:
,
故选:B.
【点睛】本题主要考查了用字母表示数,解题的关键是正确理解题意,根据题意找出等量关系列出等式.
8.C
【分析】本题考查了图形规律探究,掌握图形规律探究方法善于总结规律是解题的关键.先列出前几个图形中圆的个数,然后推论出第n个图形中圆的个数为,最后把代入求解即可.
【详解】解:第1个图形中有个圆,
第2个图形中有个圆,
第3个图形中有个圆,
…
第n个图形中有个圆,
当时,有个圆 .
故选:C .
9.A
【分析】此题主要考查了代数式的定义,代数式是有数和字母组成,表示加、减、乘、除、乘方、开方等运算的式子,或含有字母的数学表达式,注意不能含有、、、、、、等符号.
【详解】解:,,含有和,所以不是代数式,
代数式的有,,,,,,共6个.
故选:A.
10.C
【分析】本题考查了代数式的定义,代数式是由运算符号(加、减、乘、除、乘方和开方等)把数或表示数的字母连结而成的式子,单独的一个数或字母也是代数式,根据代数式的定义逐项分析即可得解.
【详解】解:A、16是代数式,故不符合题意;
B、是代数式,故不符合题意;
C、不是代数式,故符合题意;
D、是代数式,故不符合题意;
故选:C.
11.B
【分析】先求出a﹣2b的值,然后将x=﹣1代入要求的代数式,从而利用整体代入即可得出答案.
【详解】解:由题意得,当x=1时,代数式的值为2022,
∴a﹣2b﹣1=2022,
∴a﹣2b=2023,
当x=﹣1时,代数式=﹣a+2b+1=﹣(a﹣2b)+1=﹣2023+1=﹣2022.
故选:B.
【点睛】此题考查了代数式求值的知识,解答本题的关键是求出a+b的值,然后整体代入,整体思想是数学解题经常用到的,同学们要注意掌握.
12.D
【分析】由一月份新产品的研发资金为a元,根据题意可以得到2月份研发资金为a×(1+20%),而三月份在2月份的基础上又增长了20%,那么三月份的研发资金也可以用b表示出来,由此即可得解.
【详解】解:∵一月份新产品的研发资金为a元,
2月份起,每月新产品的研发资金与上月相比增长率都是20%,
∴2月份研发资金为a×(1+20%)=1.2a,
∴三月份的研发资金为b=a×(1+20%)×(1+20%)=a(1+20)2=1.44a.
故选:D.
【点睛】此题主要考查了根据实际问题列代数式,读懂题意是解答本题的关键.
13.
【分析】根据题意列式即可.
【详解】根据题意得,一种商品每件盈利为a元,售出60件,共盈利元.
故答案为:.
【点睛】本题主要考查了列代数式,解题的关键是熟练掌握总利润=单件利润×件数.
14.10x+y/y+10x
【分析】根据两位数=10×十位数字+个位数字,把相关数值代入即可得到结果.
【详解】∵个位数是x,十位数是y,对调位置后,十位数字为x,个位数字为y,
∴所得的两位数是10x+y.
故答案为:10x+y.
【点睛】本题考查了列代数式.解答本题的关键是正确理解文字语言中的关键词,从而明确其中的运算关系,正确地列出代数式.
15.相等
【分析】本题考查代数式求值,分别将和代入代数式求值即可.
【详解】解∶当时,;
当时,.
故当x分别等于1和时,代数式的两个值相等.
故答案为∶相等.
16.
【分析】本题主要考查了代数式求值,先根据题意得到,再由,把整体代入求解即可.
【详解】解:∵代数式的值是5,
∴,
∴,
故答案为:.
17.0
【分析】直接代入可得结果.
【详解】解:∵,
∴,
故答案为:0.
【点睛】本题考查了求代数式的值,直接代入并根据运算法则计算是解此题的关键.
18.(1)窗户的面积为
(2)窗户内外框总长为
(3)制作这种窗户需要的费用约是271元
【分析】本题主要考查了列代数式,代数式求值,解题的关键是理解题意熟练掌握正方形的面积公式和圆的面积公式.
(1)根据正方形面积公式和圆的面积公式进行解答即可;
(2)根据正方形周长公式和圆的周长公式进行解答即可;
(3)代入数据进行求值即可.
【详解】(1)解:∵
∴窗户的面积为 .
(2)解:∵,
∴窗户内外框总长为.
(3)解:若,购买玻璃的费用是,购买窗框的费用是,
,
当时,(元),
答:制作这种窗户需要的费用约是271元.
19.,
【分析】根据图示可知:正方形桌布的面积为a2(平方米),圆形桌面的面积为:×(a÷2)2=(平方米),所以桌布铺在圆形桌面上,垂下来的部分面积为:a2 =;铺在正方形桌面上,桌布垂下部分的面积是.
【详解】解:a2 =;
答:按图3所示把它铺在折叠前的圆形桌面上,那么桌布垂下部分的面积是;按图4所示把这块桌布铺在折叠后的正方形桌面上,垂下的面积为.
【点睛】本题主要考查列代数式以及圆与组合图形,关键利用圆的面积公式计算.
20.(1)7,10,13,16
(2)个,6067个
【分析】本题考查图形和数字类规律探究,找到变化规律是解答的关键.
(1)根据图形中〇的个数求解即可;
(2)根据前几个图形中〇的个数找到规律求解即可.
【详解】(1)解:观察图形的变化,得
第1个图形有个〇,
第2个图形有个〇,
第3个图形有个〇,
第4个图形有个〇,
则第5个图形有个〇,
故答案为:7,10,13,16;
(2)解:由(1)知,第n个图形有个〇,
∴第2022个图形有个〇.
21.;
【分析】本题考查列代数式,根据拼图,用代数式表示出拼成的长方形的长,结合周长与面积公式求解即可求得答案;
【详解】解:由题意得,
剪拼后所得的长方形的长为:,宽为:,
因此周长为:,
即:,
面积为:,
即:.
22.,见解析
【分析】分别将的值代入代数式求值后再得出结论即可.
【详解】解:当时,
当时,
当时,
当时,
当时,
当时,
当时,
当时,
发现的结论为:当取互为相反数的值时,的值相等.
【点睛】此题考查了代数式求值,解题的关键是正确代入的值求解.
23.(1)元
(2)名
(3)
(4)元
【分析】本题主要考查根据实际问题列代数式的能力,列代数式时,一般应在语言叙述的数量关系中,先读的先写,不同级运算的语言,且又要体现出先低级运算,要把代数式中代表低级运算的这部分括起来.
(1)用一个季度零花钱的总数除以3即可;
(2)全班总人数减去参加篮球赛的人数即可得出剩余人数;
(3)用油的总体积减去用去油的体积,即可得出剩余油的数量;
(4)用一件剩的钱数乘以3即可得出答案.
【详解】(1)解:小明每季度有零花钱a元,拿出b元捐给希望工程,一个季度有3个月,则平均每月剩余零花钱元;
(2)解:七年级(1)班共有a名学生,其中有b名男同学,男生的三分之一去参加篮球比赛,则班里还有人;
(3)解:某种汽车油箱装满后有油,每小时耗油,行驶了,油箱剩余油量;
(4)解:某商品原价每件a元,商场打折,现价每件b元,现买3件可以省元.
24.(1)n2
(2)①1+3+5+7+…+99=2500;②101+103+105+…+199=7500
【分析】(1)观察图形的变化可得规律,根据发现的规律即可猜想1+3+5+7+…+(2n-1)的值;
(2)①根据(1)中的规律即可求解;②根据(1)中的规律和①的结果,即可求得101+103+105+…+199的值.
【详解】(1)解:∵第(1)个图形中有1个正方形;
第(2)个图形有1+3=4个小正方形;
第(3)个图形有1+3+5=9个小正方形;
第(4)个图形有1+3+5+7=16小正方形;
……
∴1+3+5+7+…+(2n﹣1)
=()2
=n2;
故答案为:n2;
(2)解:①1+3+5+7+…+99
=()2
=502
=2500;
②∵1+3+5+7+…+199
=()2
=10000,
∴101+103+105+…+199
=10000﹣2500
=7500.
【点睛】本题考查了规律型-图形的变化类,解决本题的关键是观察图形的变化寻找规律.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.1用字母表示数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列选项中,能用表示的是( ).
A.整条线段的长度: B.整条线段的长度:
C.这个长方形的周长: D.这个图形的面积:
2.如果,那么代数式的值是( )
A.0 B.5 C.7 D.9
3.当时,的值是( )
A.5 B.13 C.21 D.25
4.已知每个人做某项工作的效率相同,个人做d天可以完成,若增加人,则完成工作所需的天数为( ).
A. B. C. D.
5.若三角形的一条边长为,这条边上的高为,则这个三角形的面积可以表示为( )
A. B. C. D.
6.某数的平方的5倍与1的差的一半,用代数式表示是( )
A. B. C. D.
7.甲袋有a千克大米,乙袋有b千克大米,如果从甲袋拿出9千克大米放入乙袋,那么甲、乙两袋质量相等.列成等式是( ).
A. B. C. D.
8.如图,是由正方形和相同大小的圆按照一定规律摆放而成,按此规律,则第10个图形中圆的个数是( )
A.40 B.41 C.31 D.19
9.在,,,,,,,中,代数式有( )
A.个 B.个 C.个 D.个
10.下列各式不是代数式的是( )
A.16 B. C. D.
11.当x=1时,代数式的值是2022,则当x=﹣1时,代数式的值是( )
A.2021 B.﹣2022 C.﹣2021 D.2022
12.某企业今年一月份投入新产品的研发资金为a万元,以后每月投入新产品的研发资金与上月相比增长率都是20%.该厂今年三月份投入新产品的研发资金为b万元,则( )
A. B. C. D.
二、填空题
13.一种商品每件盈利为a元,售出60件,共盈利 元(用含a的式子表示)
14.一个两位数,个位数字是x,十位数字是y,若个位数字与十位数字对调,则所得的新的两位数是 .
15.当x分别等于1和时,代数式的两个值 .(填“相等”“互为相反数”或“互为倒数”)
16.若代数式的值是5,则代数式 .
17.当时,代数式的值是 .
三、解答题
18.如图是一幢公寓窗户的形状,其上部是半圆形,下部是边长相同的四个小正方形,已知下部的小正方形的边长为,计算:
(1)窗户的总面积是多少?(窗框面积忽略不计)
(2)窗户内外框的总长是多少?
(3)如果窗户上安装的是玻璃,购买玻璃的费用是40元/,购买窗框的费用是24元/,当时,制作一扇窗户需要的费用是多少元?(取).
19.如图(1)(2),某餐桌桌面可由圆形折叠成正方形(图中阴影表示可折叠部分).已知折叠前圆形桌面的直径为,折叠成正方形后其边长为.如果一块正方形桌布的边长为,并按图(3)所示把它铺在折叠前的圆形桌面上,那么桌布垂下部分的面积是多少?如果按图(4)所示把这块桌布铺在折叠后的正方形桌面上呢?
20.观察下列图中所示的一系列图形,它们是按一定规律排列的,
(1)填空:
图形编号 第1个 第2个 第3个 第4个 第5个
〇的个数 4
(2)按这种规律排列下去,第n个图形有多少个〇?第2022个图形有多少个〇?
21.如图,将边长为的正方形纸片剪去一个边长为a的正方形后,剩余部分可剪拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为3,请解答下列问题:
分别计算剪拼后所得的长方形的C周长和面积S(用含a的方程表示);
22.当时,分别求出代数式的值.你发现了什么?
23.回答下列问题:
(1)小明每季度有零花钱a元,拿出b元捐给爱心基金,平均每月剩余的零花钱是多少?
(2)七年级(1)班共有a名学生,其中有b名男生,男生的三分之一去参加篮球比赛了,班级剩余多少人?
(3)某种汽车油箱装满后有油,每小时耗油,行驶了,油箱剩余油量是多少?
(4)某商品原价每件a元,商场打折,现价每件b元,现买3件可以省多少元?
24.用同样大小的两种不同颜色的正方形纸片,按下图方式拼正方形.
第(1)个图形中有1个正方形;
第(2)个图形有1+3=4个小正方形;
第(3)个图形有1+3+5=9个小正方形;
第(4)个图形有1+3+5+7=16小正方形;
……
(1)根据上面的发现我们可以猜想:1+3+5+7+…+(2n﹣1)=______(用含n的代数式表示);
(2)请根据你的发现计算:
①1+3+5+7+…+99;
②101+103+105+…+199.
《2.1用字母表示数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D D D D B C A C
题号 11 12
答案 B D
1.C
【分析】本题考查了列代数式,解题的关键是掌握线段的长度和图形的周长、面积计算方法.分别计算各选项的结果,化简即可判断.
【详解】解:A、整条线段的长度为,故A不合题意;
B、整条线段的长度为,故B不合题意;
C、这个长方形的周长为,故C符合题意;
D、这个图形的面积为,故D不合题意.
故选:C.
2.D
【分析】本题考查了代数式求值:将代入,进行计算即可.
【详解】解:∵,
∴,
故选:D.
3.D
【分析】将代入原式,即可解答.
【详解】解:当时,
原式.
故选:D.
【点睛】本题考查了代入代数式的代入求值,熟练计算是解题的关键.
4.D
【分析】本题考查了用字母表示数,设每个人做某项工作的效率为1,则这项工作总量为,若增加r人,现在总人数是人,用工作总量除以总人数,即可求出完成工作所需的天数.
【详解】解:设每个人做某项工作的效率为1,则这项工作总量为,若增加r人,
则完成工作所需的天数为,
故选:D.
5.D
【分析】根据三角形面积公式即可求解.
【详解】解:三角形的面积=底高
故选:D.
【点睛】本题考查了用字母表示数,解题关键是理解题意正确列出代数式.
6.D
【分析】本题考查了列代数式.数的平方为,的5倍是,再表示与1的差,最后表示出差的一半,即可.
【详解】解:某数的平方的5倍与1的差的一半,用代数式表示是.
故选:D.
7.B
【分析】根据题意,找出数量关系,即可而出等式.
【详解】解:根据题意可得:
,
故选:B.
【点睛】本题主要考查了用字母表示数,解题的关键是正确理解题意,根据题意找出等量关系列出等式.
8.C
【分析】本题考查了图形规律探究,掌握图形规律探究方法善于总结规律是解题的关键.先列出前几个图形中圆的个数,然后推论出第n个图形中圆的个数为,最后把代入求解即可.
【详解】解:第1个图形中有个圆,
第2个图形中有个圆,
第3个图形中有个圆,
…
第n个图形中有个圆,
当时,有个圆 .
故选:C .
9.A
【分析】此题主要考查了代数式的定义,代数式是有数和字母组成,表示加、减、乘、除、乘方、开方等运算的式子,或含有字母的数学表达式,注意不能含有、、、、、、等符号.
【详解】解:,,含有和,所以不是代数式,
代数式的有,,,,,,共6个.
故选:A.
10.C
【分析】本题考查了代数式的定义,代数式是由运算符号(加、减、乘、除、乘方和开方等)把数或表示数的字母连结而成的式子,单独的一个数或字母也是代数式,根据代数式的定义逐项分析即可得解.
【详解】解:A、16是代数式,故不符合题意;
B、是代数式,故不符合题意;
C、不是代数式,故符合题意;
D、是代数式,故不符合题意;
故选:C.
11.B
【分析】先求出a﹣2b的值,然后将x=﹣1代入要求的代数式,从而利用整体代入即可得出答案.
【详解】解:由题意得,当x=1时,代数式的值为2022,
∴a﹣2b﹣1=2022,
∴a﹣2b=2023,
当x=﹣1时,代数式=﹣a+2b+1=﹣(a﹣2b)+1=﹣2023+1=﹣2022.
故选:B.
【点睛】此题考查了代数式求值的知识,解答本题的关键是求出a+b的值,然后整体代入,整体思想是数学解题经常用到的,同学们要注意掌握.
12.D
【分析】由一月份新产品的研发资金为a元,根据题意可以得到2月份研发资金为a×(1+20%),而三月份在2月份的基础上又增长了20%,那么三月份的研发资金也可以用b表示出来,由此即可得解.
【详解】解:∵一月份新产品的研发资金为a元,
2月份起,每月新产品的研发资金与上月相比增长率都是20%,
∴2月份研发资金为a×(1+20%)=1.2a,
∴三月份的研发资金为b=a×(1+20%)×(1+20%)=a(1+20)2=1.44a.
故选:D.
【点睛】此题主要考查了根据实际问题列代数式,读懂题意是解答本题的关键.
13.
【分析】根据题意列式即可.
【详解】根据题意得,一种商品每件盈利为a元,售出60件,共盈利元.
故答案为:.
【点睛】本题主要考查了列代数式,解题的关键是熟练掌握总利润=单件利润×件数.
14.10x+y/y+10x
【分析】根据两位数=10×十位数字+个位数字,把相关数值代入即可得到结果.
【详解】∵个位数是x,十位数是y,对调位置后,十位数字为x,个位数字为y,
∴所得的两位数是10x+y.
故答案为:10x+y.
【点睛】本题考查了列代数式.解答本题的关键是正确理解文字语言中的关键词,从而明确其中的运算关系,正确地列出代数式.
15.相等
【分析】本题考查代数式求值,分别将和代入代数式求值即可.
【详解】解∶当时,;
当时,.
故当x分别等于1和时,代数式的两个值相等.
故答案为∶相等.
16.
【分析】本题主要考查了代数式求值,先根据题意得到,再由,把整体代入求解即可.
【详解】解:∵代数式的值是5,
∴,
∴,
故答案为:.
17.0
【分析】直接代入可得结果.
【详解】解:∵,
∴,
故答案为:0.
【点睛】本题考查了求代数式的值,直接代入并根据运算法则计算是解此题的关键.
18.(1)窗户的面积为
(2)窗户内外框总长为
(3)制作这种窗户需要的费用约是271元
【分析】本题主要考查了列代数式,代数式求值,解题的关键是理解题意熟练掌握正方形的面积公式和圆的面积公式.
(1)根据正方形面积公式和圆的面积公式进行解答即可;
(2)根据正方形周长公式和圆的周长公式进行解答即可;
(3)代入数据进行求值即可.
【详解】(1)解:∵
∴窗户的面积为 .
(2)解:∵,
∴窗户内外框总长为.
(3)解:若,购买玻璃的费用是,购买窗框的费用是,
,
当时,(元),
答:制作这种窗户需要的费用约是271元.
19.,
【分析】根据图示可知:正方形桌布的面积为a2(平方米),圆形桌面的面积为:×(a÷2)2=(平方米),所以桌布铺在圆形桌面上,垂下来的部分面积为:a2 =;铺在正方形桌面上,桌布垂下部分的面积是.
【详解】解:a2 =;
答:按图3所示把它铺在折叠前的圆形桌面上,那么桌布垂下部分的面积是;按图4所示把这块桌布铺在折叠后的正方形桌面上,垂下的面积为.
【点睛】本题主要考查列代数式以及圆与组合图形,关键利用圆的面积公式计算.
20.(1)7,10,13,16
(2)个,6067个
【分析】本题考查图形和数字类规律探究,找到变化规律是解答的关键.
(1)根据图形中〇的个数求解即可;
(2)根据前几个图形中〇的个数找到规律求解即可.
【详解】(1)解:观察图形的变化,得
第1个图形有个〇,
第2个图形有个〇,
第3个图形有个〇,
第4个图形有个〇,
则第5个图形有个〇,
故答案为:7,10,13,16;
(2)解:由(1)知,第n个图形有个〇,
∴第2022个图形有个〇.
21.;
【分析】本题考查列代数式,根据拼图,用代数式表示出拼成的长方形的长,结合周长与面积公式求解即可求得答案;
【详解】解:由题意得,
剪拼后所得的长方形的长为:,宽为:,
因此周长为:,
即:,
面积为:,
即:.
22.,见解析
【分析】分别将的值代入代数式求值后再得出结论即可.
【详解】解:当时,
当时,
当时,
当时,
当时,
当时,
当时,
当时,
发现的结论为:当取互为相反数的值时,的值相等.
【点睛】此题考查了代数式求值,解题的关键是正确代入的值求解.
23.(1)元
(2)名
(3)
(4)元
【分析】本题主要考查根据实际问题列代数式的能力,列代数式时,一般应在语言叙述的数量关系中,先读的先写,不同级运算的语言,且又要体现出先低级运算,要把代数式中代表低级运算的这部分括起来.
(1)用一个季度零花钱的总数除以3即可;
(2)全班总人数减去参加篮球赛的人数即可得出剩余人数;
(3)用油的总体积减去用去油的体积,即可得出剩余油的数量;
(4)用一件剩的钱数乘以3即可得出答案.
【详解】(1)解:小明每季度有零花钱a元,拿出b元捐给希望工程,一个季度有3个月,则平均每月剩余零花钱元;
(2)解:七年级(1)班共有a名学生,其中有b名男同学,男生的三分之一去参加篮球比赛,则班里还有人;
(3)解:某种汽车油箱装满后有油,每小时耗油,行驶了,油箱剩余油量;
(4)解:某商品原价每件a元,商场打折,现价每件b元,现买3件可以省元.
24.(1)n2
(2)①1+3+5+7+…+99=2500;②101+103+105+…+199=7500
【分析】(1)观察图形的变化可得规律,根据发现的规律即可猜想1+3+5+7+…+(2n-1)的值;
(2)①根据(1)中的规律即可求解;②根据(1)中的规律和①的结果,即可求得101+103+105+…+199的值.
【详解】(1)解:∵第(1)个图形中有1个正方形;
第(2)个图形有1+3=4个小正方形;
第(3)个图形有1+3+5=9个小正方形;
第(4)个图形有1+3+5+7=16小正方形;
……
∴1+3+5+7+…+(2n﹣1)
=()2
=n2;
故答案为:n2;
(2)解:①1+3+5+7+…+99
=()2
=502
=2500;
②∵1+3+5+7+…+199
=()2
=10000,
∴101+103+105+…+199
=10000﹣2500
=7500.
【点睛】本题考查了规律型-图形的变化类,解决本题的关键是观察图形的变化寻找规律.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
