6.2探索活动:成长的脚印暑假预习练(含解析)北师大版数学五年级上册
文档属性
| 名称 | 6.2探索活动:成长的脚印暑假预习练(含解析)北师大版数学五年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 16:35:05 | ||
图片预览


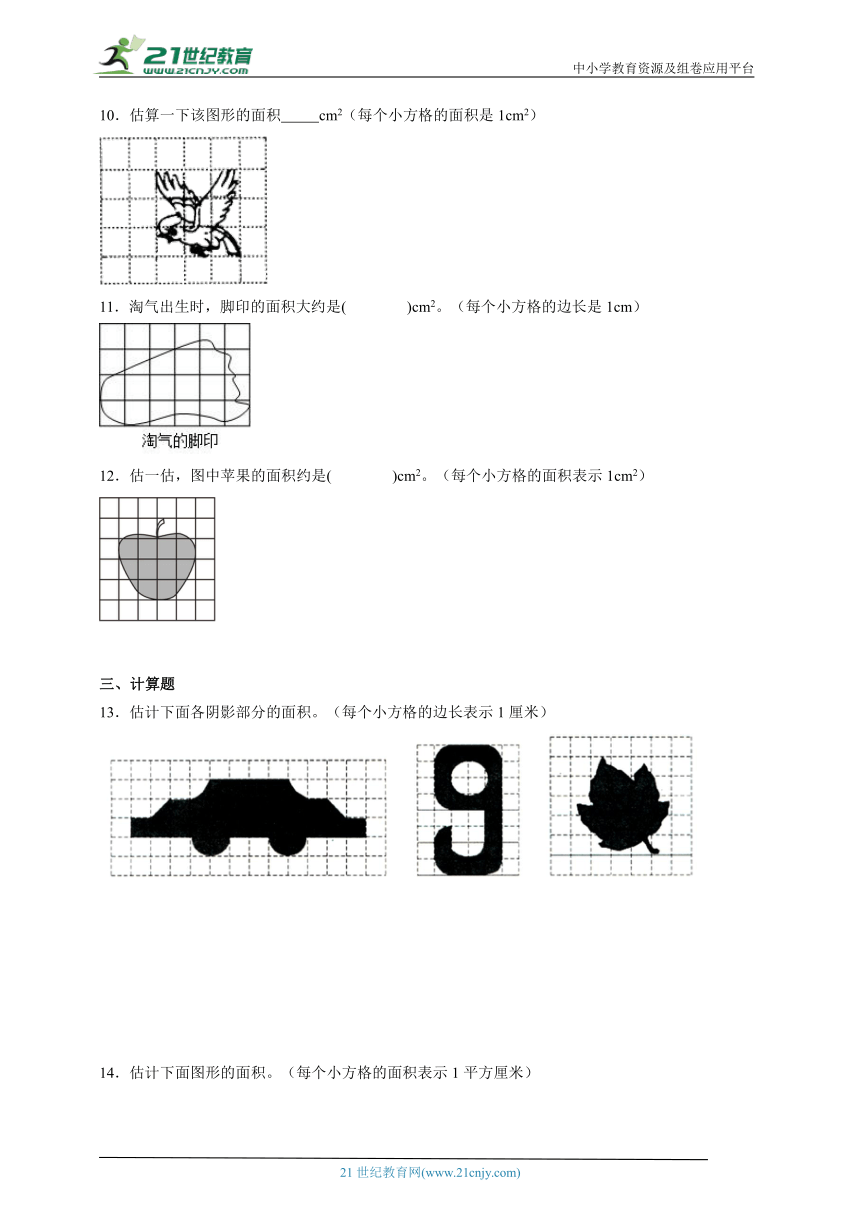
文档简介
中小学教育资源及组卷应用平台
6.2探索活动:成长的脚印
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面图形中,( )的面积与其它两个的面积不相等。(图中每个小方格的边长表示lcm)
A.A B.B C.C
2.关于下面两个图形阴影部分的面积,说法正确的是( )。
图1 图2
A.图1>图2 B.图1<图2 C.图1=图2
二、填空题
3.每个小方格的面积均为1cm2,估一估方格纸上图案的面积是( )cm2。
4.图形A、图形B、图形C的面积分别是( )、( )、( )。图形D的面积大约是( )。(每小格面积是1cm2)
5.估计下列图形的面积,与同伴说一说你是怎么做的。(每个小方格的边长表示1)
面积约为( ) 面积约为( )
6.如果从一个多边形的一个顶点出发,分别连接这个顶点与其余各顶点,可将这个多边形分割成2011个三角形,那么此多边形的边数为 .
7.估计方格纸上图形的面积.(每个小方格的边长表示1 m )
m m
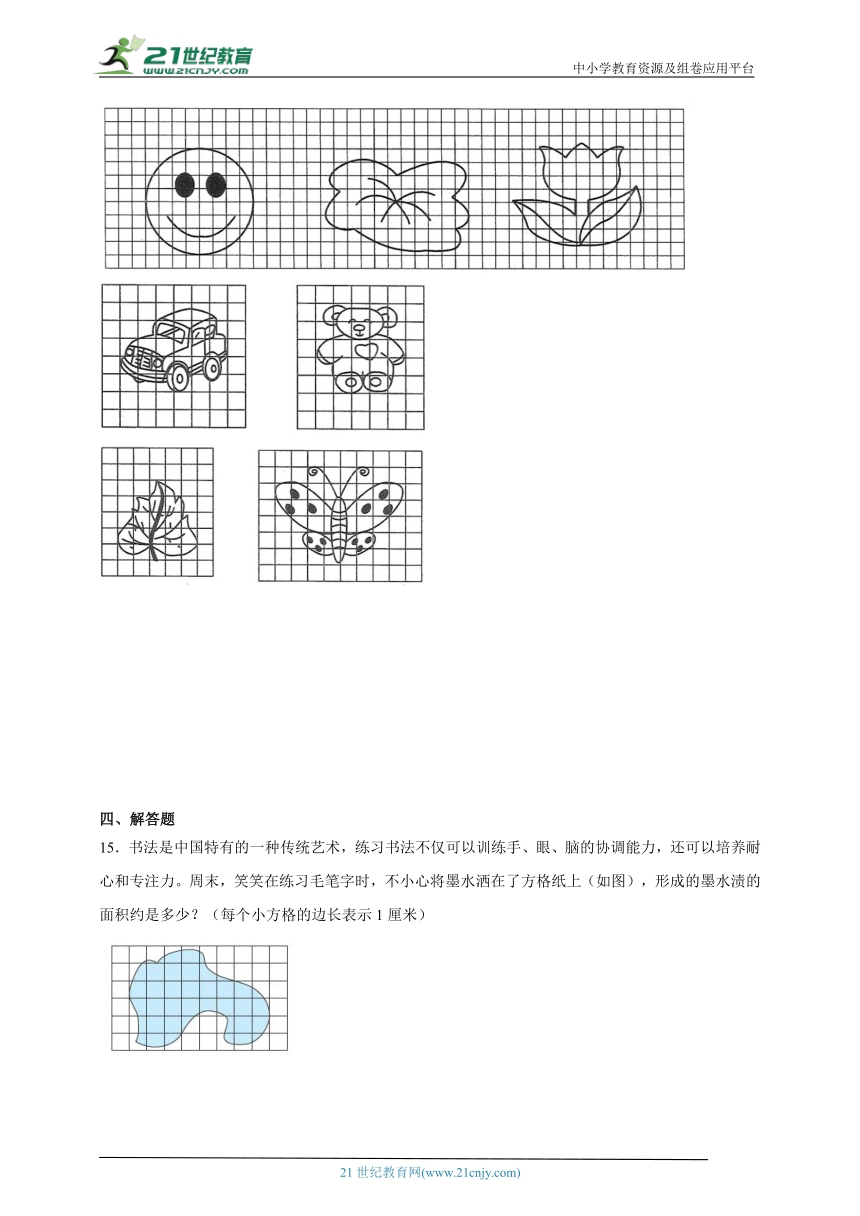
8.估计下列图形的面积。(每个小方格的边长表示1cm)
面积约为( )cm2面积约为( )cm2
9.估算一下,该图形阴影的面积 cm2(每个小方格的面积是1cm2)。
10.估算一下该图形的面积 cm2(每个小方格的面积是1cm2)
11.淘气出生时,脚印的面积大约是( )cm2。(每个小方格的边长是1cm)
12.估一估,图中苹果的面积约是( )cm2。(每个小方格的面积表示1cm2)
三、计算题
13.估计下面各阴影部分的面积。(每个小方格的边长表示1厘米)
14.估计下面图形的面积。(每个小方格的面积表示1平方厘米)
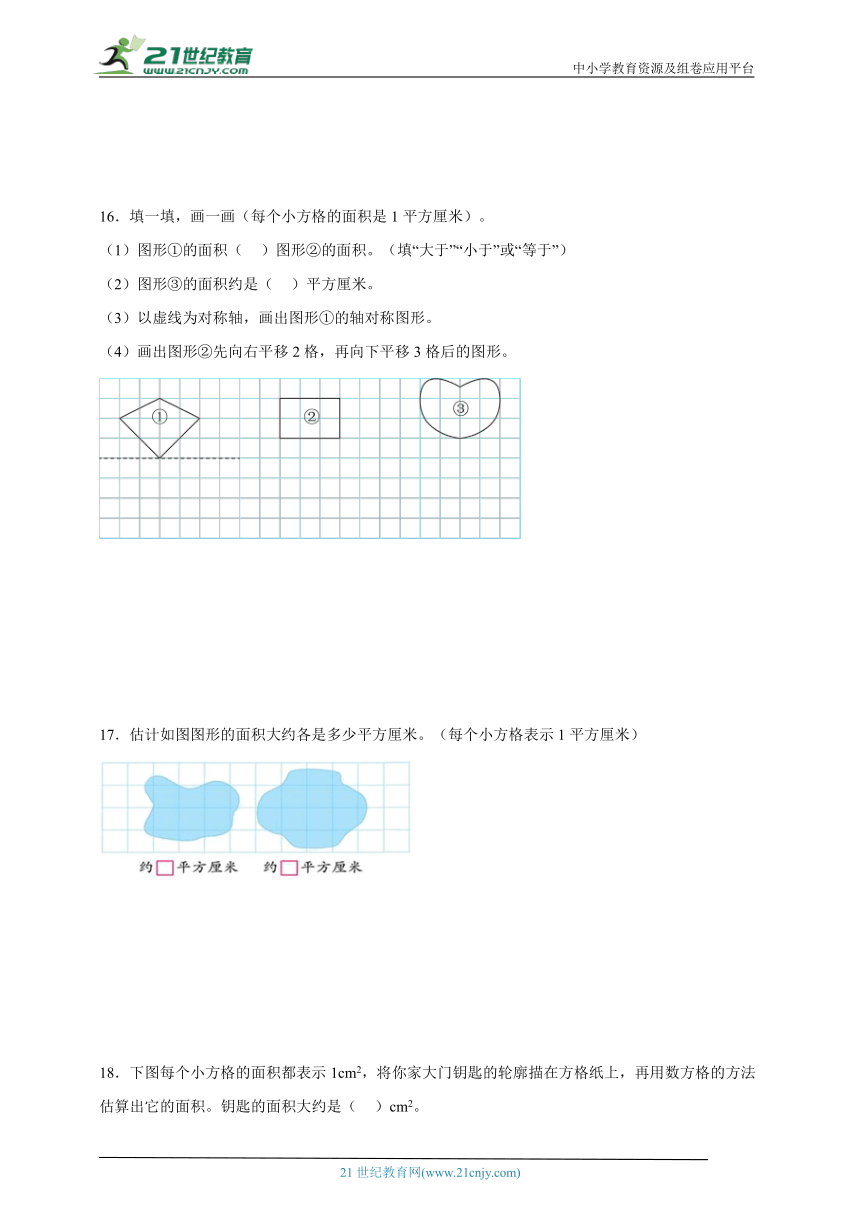
四、解答题
15.书法是中国特有的一种传统艺术,练习书法不仅可以训练手、眼、脑的协调能力,还可以培养耐心和专注力。周末,笑笑在练习毛笔字时,不小心将墨水洒在了方格纸上(如图),形成的墨水渍的面积约是多少?(每个小方格的边长表示1厘米)
16.填一填,画一画(每个小方格的面积是1平方厘米)。
(1)图形①的面积( )图形②的面积。(填“大于”“小于”或“等于”)
(2)图形③的面积约是( )平方厘米。
(3)以虚线为对称轴,画出图形①的轴对称图形。
(4)画出图形②先向右平移2格,再向下平移3格后的图形。
17.估计如图图形的面积大约各是多少平方厘米。(每个小方格表示1平方厘米)
18.下图每个小方格的面积都表示1cm2,将你家大门钥匙的轮廓描在方格纸上,再用数方格的方法估算出它的面积。钥匙的面积大约是( )cm2。
19.市政公司准备给新玛特商场门口的广场(如图所示)重新铺地砖,每个方格表示1平方米。
(1)估计它的面积大约是多大?
(2)如果1平方米大约要4块瓷砖,每块瓷砖4.8元,大约需要多少钱?
《6.2探索活动:成长的脚印》参考答案
题号 1 2
答案 A C
1.A
【分析】图形A是三角形,因三角形面积=底×高÷2,将数据代入可求得三角形面积。
图形B和C可用数格子的方法数出有多少个格子,从而知道它们的面积。据此解答。
【详解】每个格子的面积:1×1=1()
图形A面积:6×3÷2
=18÷2
=9()
图形B面积:13
图形C面积:13
故答案为:A
【点睛】对规则图形,可用公式求得面积,对不规则的图形,本题可用数格子的方法求得面积。
2.C
【分析】不规则图形的面积估算方法:数格子,分别数出满格和不满格的数量,不满格的数量按半格计算,再加上满格的数量,就是不规则图形的格子数,最后乘每个小方格的面积即是不规则图形的面积。
据此分别数出图1、图2阴影部分的格子数,因为每个小方格的面积相等,所以只需比较两个图形阴影部分格子数的多少,格子数多的,面积就大。
【详解】图1阴影部分的格子数:
(13+6÷2)×4
=(13+3)×4
=16×4
=64(个)
图2阴影部分的格子数:
48+32÷2
=48+16
=64(个)
64=64,所以图1阴影部分的面积=图2阴影部分的面积。
故答案为:C
3.33
【分析】可以借助方格图数格子估算不规则图形的面积。用数格子估计不规则图形面积的方法:分别数出整数的格数和不满1格的格数;把不满1格的格数按半格计算,加上整数格,最后估算出面积。
【详解】通过数格子,图案中有16个整方格,有34个不是整方格。
(16+34÷2)×1
=(16+17)×1
=33×1
=33(cm2)
方格纸上图案的面积是33cm2。
【点睛】可以借助方格图数格子估算不规则图形的面积,也可以把不规则图形看成近似于规则的图形估算面积。掌握用数格子估计不规则图形面积的方法是解题的关键。
4. 8cm2/8平方厘米 5cm2/5平方厘米 12cm2/12平方厘米 15cm2
【分析】平行四边形面积=底×高,三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2,正方形面积=边长×边长,长方形面积=长×宽。
如图,图形A的面积=平行四边形面积×2+正方形面积,图形B的面积=大三角形的面积+小三角形的面积,图形C的面积=平行四边形面积+2个梯形面积+长方形面积,图形D可以看成近似的梯形。
【详解】图形A:2×1×2+2×2
=4+4
=8(cm2)
图形B:4×2÷2+2×1÷2
=4+1
=5(cm2)
图形C:1×1+(1+5)×2÷2+(1+5)×1÷2+2×1
=1+6×2÷2+6×1÷2+2
=1+6+3+2
=12(cm2)
图形D:(3+7)×3÷2
=10×3÷2
=15(cm2)
图形A、图形B、图形C的面积分别是8cm2、5cm2、12cm2。图形D的面积大约是15cm2。(最后一空答案不唯一)
5. 60 29
【分析】数方格估面积,先数满格,再数不满一格的,不满一格的按半格算,据此计算填空即可(答案不唯一)。
【详解】由分析可得:
老虎:满格47格,不满格的有26格,
47+26÷2
=47+13
=60(格)(答案不唯一)
树叶:满格的有12格,不满格的有34格,
12+34÷2
=12+17
=29(格)(答案不唯一)
综上所述:左图面积为60cm2,右图面积为29cm2。
6.2013
【详解】多边形的边数是:2011+2=2013
故答案是:2013.
7. 87 124
【详解】略
8. 7 6
【分析】利用数方格的方法,先数整格,再数不满一格的,不满一格的按半格计算。据此解答。
【详解】2+10×0.5
=2+5
=7(cm2)
2+8×0.5
=2+4
=6(cm2)
【点睛】此题考查的目的是理解掌握不规则图形面积的计算方法及应用。
9.26(答案在1-2范围之间浮动皆可)
【分析】数该图形所占方格数时,对于方格不是全部沾满的情况而言,若占用的一半的记作方格面积的二分之一,占用一半以上的面积是记作满格,将不满一半的方格忽略不计。
【详解】通过观察图形可知,该图形阴影的面积有26 cm。
【点睛】此题主要考查学生对图形面积估算的能力,占用的一半的记作方格面积的二分之一,占用一半以上的面积是记作满格,将不满一半的方格忽略不计。
10.7
【分析】数该图形所占方格数时,对于方格不是全部占满的情况而言,若占用的一半的记作方格面积的二分之一,占用一半以上的面积是记作满格,将不满一半的方格忽略不计。
【详解】该图形1个全部沾满,0个占方格面积的一半,6个占方格一半以上的面积,2个占不满方格一半。
1+6=7(cm2)
故答案为:7
【点睛】本题考查不规则图形的面积求法,利用数格子法来做。
11.12.5
【分析】用数格的方法即可估测出淘气出生时脚印的面积,整格的按1平方厘米计算,不足格的按半格(即0.5平方厘米)计算,再把二者相加就是淘气出生时脚印的面积大约数。
【详解】整格数:5格
5×1=5(cm2)
不足格:15格
15×0.5=7.5(cm2)
5+7.5=12.5(cm2)
即淘气出生时,脚印的面积大约是12.5cm2。
【点睛】用数方格的方法估测不规则图形的面积,分整格和不足格,不足格一律按半格计算。
12.10
【分析】看图可知,满格的一共有4格,也就是4cm2;不满一格的有12格,不满一格的都按半格算,12÷2=6(cm2);再将两部分的面积相加,可估出图中苹果的面积。
【详解】4+12÷2
=4+6
=10(cm2)
所以,图中苹果的面积约是10cm2。
(答案不唯一)
13.28平方厘米;20.5平方厘米;15.5平方厘米
【分析】根据不规则图形面积的计算方法,可以数格子,不满1格的按半格计算,根据正方形面积公式:S=边长×边长,求出1个小方格的面积,用数出的小方格个数乘面积即可。
【详解】由分析可得:
1×1=1(平方厘米)
左图:该图形由24个小方格和8个不满格的小方格组成
24×1+8×1÷2
=24+8÷2
=24+4
=28(平方厘米)
中间的图:该图形可以看作由20个小方格和1个不满格的小方格组成
20×1+1×1÷2
=20+1÷2
=20+0.5
=20.5(平方厘米)
右图:该图形由9个小方格和13个不满格的小方格组成
9×1+13×1÷2
=9+13÷2
=9+6.5
=15.5(平方厘米)
14.44平方厘米;55平方厘米;40平方厘米
17平方厘米;15平方厘米;14平方厘米;20平方厘米(答案均不唯一)
【分析】可以借助方格图数格子估算不规则图形的面积。用数格子估计不规则图形面积的方法:分别数出整数的格数和不满1格的格数;把不满1格的格数按半格计算,加上整数格,最后估算出面积。
【详解】(1)图中有32个整格,不满一格的有24格,则面积为:
(32+24÷2)×1
=(32+12)×1
=44×1
=44(平方厘米)
(2)图中有44个整格,不满一格的有22格,则面积为:
(44+22÷2)×1
=(44+11)×1
=55×1
=55(平方厘米)
(3)图中有27个整格,不满一格的有26格,则面积为:
(27+26÷2)×1
=(27+13)×1
=40×1
=40(平方厘米)
(4)图中有11个整格,不满一格的有12格,则面积为:
(11+12÷2)×1
=(11+6)×1
=17×1
=17(平方厘米)
(5)图中有7个整格,不满一格的有16格,则面积为:
(7+16÷2)×1
=(7+8)×1
=15×1
=15(平方厘米)
(6)图中有7个整格,不满一格的有14格,则面积为:
(7+14÷2)×1
=(7+7)×1
=14×1
=14(平方厘米)
(7)图中有8个整格,不满一格的有24格,则面积为:
(8+24÷2)×1
=(8+12)×1
=20×1
=20(平方厘米)
15.28平方厘米
【分析】可以把不规则图形看成一个近似的长方形,长方形的长近似7厘米,宽近似为4厘米,再用长方形的面积=长×宽,代入数据计算求解。
【详解】7×4=28(平方厘米)
答:形成的墨水渍的面积约是28平方厘米。
16.(1)等于
(2)7
(3)(4)见详解
【分析】(1)每个小方格的面积是1平方厘米,则每个小方格的边长为1厘米,再根据三角形的面积公式:S=ah÷2,长方形的面积公式:S=ab,据此分别求出图形①和图形②的面积,再进行比较即可;
(2)求不规则图形的面积,先数该图形占几个整格数,再数占多少个不满整格数,不满整格数按半格算,两个半格算一个整格,据此计算即可;
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,画出对应点,然后顺次连接各点即可;
(4)将图形②的各点先向右平移2格,再向下平移3格后,然后再顺次连接各点即可。
【详解】(1)图形①的面积:
4×1÷2+4×2÷2
=4÷2+8÷2
=2+4
=6(平方厘米)
图形②的面积:
3×2=6(平方厘米)
则图形①的面积等于图形②的面积。
(2)共有2个整格,10个半格
2×1+10÷2×1
=2+5
=7(平方厘米)
则图形③的面积约是7平方厘米。
(3)(4)如图:
17.见详解
【分析】如下图所示:
左图的面积大约等于大长方形加2个小正方形的面积即可;
右图的面积大约等于大正方形的面积加2个小正方形的面积即可。
【详解】3×2+2
=6+2
=8(平方厘米)
3×3+2×1
=9+2
=11(平方厘米)
【点睛】解答此题,要注意认真分析图形,可以将所给的图形分割成我们常见的图形,弄清图形所占的方格数,然后再计算图形的面积即可。
18.8
【分析】用数格子法算不规则图形的面积,可以把小于半格的不计,大于等于半格的计作一格,整格有4格,大于等于半格的有4格,所以钥匙总面积大约是8格,即8 cm2。
【详解】由分析可知:
4+4=8()
所以钥匙的面积大约是8 cm2。
【点睛】本题考查用数格子法算不规则图形的面积,注意:可以把小于半格的不计,大于等于半格的计作一格。
19.(1)72平方米
(2)1382.4元
【分析】(1)先数出方格的多少,计算出它的大约面积是多少;
(2)用广场的面积×4求出需要多少块瓷砖,再乘每块瓷砖的单价,即可解答。
【详解】(1)可数出72个方格,每个方格是1平方米
72×1=72(平方米)
答:它的面积大约72平方米。
(2)72×4×4.8
=288×4.8
=1382.4(元)
答:大约需要1382.4元。
【点睛】本题考查面积的估算,要仔细数出小格的数量,是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.2探索活动:成长的脚印
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面图形中,( )的面积与其它两个的面积不相等。(图中每个小方格的边长表示lcm)
A.A B.B C.C
2.关于下面两个图形阴影部分的面积,说法正确的是( )。
图1 图2
A.图1>图2 B.图1<图2 C.图1=图2
二、填空题
3.每个小方格的面积均为1cm2,估一估方格纸上图案的面积是( )cm2。
4.图形A、图形B、图形C的面积分别是( )、( )、( )。图形D的面积大约是( )。(每小格面积是1cm2)
5.估计下列图形的面积,与同伴说一说你是怎么做的。(每个小方格的边长表示1)
面积约为( ) 面积约为( )
6.如果从一个多边形的一个顶点出发,分别连接这个顶点与其余各顶点,可将这个多边形分割成2011个三角形,那么此多边形的边数为 .
7.估计方格纸上图形的面积.(每个小方格的边长表示1 m )
m m
8.估计下列图形的面积。(每个小方格的边长表示1cm)
面积约为( )cm2面积约为( )cm2
9.估算一下,该图形阴影的面积 cm2(每个小方格的面积是1cm2)。
10.估算一下该图形的面积 cm2(每个小方格的面积是1cm2)
11.淘气出生时,脚印的面积大约是( )cm2。(每个小方格的边长是1cm)
12.估一估,图中苹果的面积约是( )cm2。(每个小方格的面积表示1cm2)
三、计算题
13.估计下面各阴影部分的面积。(每个小方格的边长表示1厘米)
14.估计下面图形的面积。(每个小方格的面积表示1平方厘米)
四、解答题
15.书法是中国特有的一种传统艺术,练习书法不仅可以训练手、眼、脑的协调能力,还可以培养耐心和专注力。周末,笑笑在练习毛笔字时,不小心将墨水洒在了方格纸上(如图),形成的墨水渍的面积约是多少?(每个小方格的边长表示1厘米)
16.填一填,画一画(每个小方格的面积是1平方厘米)。
(1)图形①的面积( )图形②的面积。(填“大于”“小于”或“等于”)
(2)图形③的面积约是( )平方厘米。
(3)以虚线为对称轴,画出图形①的轴对称图形。
(4)画出图形②先向右平移2格,再向下平移3格后的图形。
17.估计如图图形的面积大约各是多少平方厘米。(每个小方格表示1平方厘米)
18.下图每个小方格的面积都表示1cm2,将你家大门钥匙的轮廓描在方格纸上,再用数方格的方法估算出它的面积。钥匙的面积大约是( )cm2。
19.市政公司准备给新玛特商场门口的广场(如图所示)重新铺地砖,每个方格表示1平方米。
(1)估计它的面积大约是多大?
(2)如果1平方米大约要4块瓷砖,每块瓷砖4.8元,大约需要多少钱?
《6.2探索活动:成长的脚印》参考答案
题号 1 2
答案 A C
1.A
【分析】图形A是三角形,因三角形面积=底×高÷2,将数据代入可求得三角形面积。
图形B和C可用数格子的方法数出有多少个格子,从而知道它们的面积。据此解答。
【详解】每个格子的面积:1×1=1()
图形A面积:6×3÷2
=18÷2
=9()
图形B面积:13
图形C面积:13
故答案为:A
【点睛】对规则图形,可用公式求得面积,对不规则的图形,本题可用数格子的方法求得面积。
2.C
【分析】不规则图形的面积估算方法:数格子,分别数出满格和不满格的数量,不满格的数量按半格计算,再加上满格的数量,就是不规则图形的格子数,最后乘每个小方格的面积即是不规则图形的面积。
据此分别数出图1、图2阴影部分的格子数,因为每个小方格的面积相等,所以只需比较两个图形阴影部分格子数的多少,格子数多的,面积就大。
【详解】图1阴影部分的格子数:
(13+6÷2)×4
=(13+3)×4
=16×4
=64(个)
图2阴影部分的格子数:
48+32÷2
=48+16
=64(个)
64=64,所以图1阴影部分的面积=图2阴影部分的面积。
故答案为:C
3.33
【分析】可以借助方格图数格子估算不规则图形的面积。用数格子估计不规则图形面积的方法:分别数出整数的格数和不满1格的格数;把不满1格的格数按半格计算,加上整数格,最后估算出面积。
【详解】通过数格子,图案中有16个整方格,有34个不是整方格。
(16+34÷2)×1
=(16+17)×1
=33×1
=33(cm2)
方格纸上图案的面积是33cm2。
【点睛】可以借助方格图数格子估算不规则图形的面积,也可以把不规则图形看成近似于规则的图形估算面积。掌握用数格子估计不规则图形面积的方法是解题的关键。
4. 8cm2/8平方厘米 5cm2/5平方厘米 12cm2/12平方厘米 15cm2
【分析】平行四边形面积=底×高,三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2,正方形面积=边长×边长,长方形面积=长×宽。
如图,图形A的面积=平行四边形面积×2+正方形面积,图形B的面积=大三角形的面积+小三角形的面积,图形C的面积=平行四边形面积+2个梯形面积+长方形面积,图形D可以看成近似的梯形。
【详解】图形A:2×1×2+2×2
=4+4
=8(cm2)
图形B:4×2÷2+2×1÷2
=4+1
=5(cm2)
图形C:1×1+(1+5)×2÷2+(1+5)×1÷2+2×1
=1+6×2÷2+6×1÷2+2
=1+6+3+2
=12(cm2)
图形D:(3+7)×3÷2
=10×3÷2
=15(cm2)
图形A、图形B、图形C的面积分别是8cm2、5cm2、12cm2。图形D的面积大约是15cm2。(最后一空答案不唯一)
5. 60 29
【分析】数方格估面积,先数满格,再数不满一格的,不满一格的按半格算,据此计算填空即可(答案不唯一)。
【详解】由分析可得:
老虎:满格47格,不满格的有26格,
47+26÷2
=47+13
=60(格)(答案不唯一)
树叶:满格的有12格,不满格的有34格,
12+34÷2
=12+17
=29(格)(答案不唯一)
综上所述:左图面积为60cm2,右图面积为29cm2。
6.2013
【详解】多边形的边数是:2011+2=2013
故答案是:2013.
7. 87 124
【详解】略
8. 7 6
【分析】利用数方格的方法,先数整格,再数不满一格的,不满一格的按半格计算。据此解答。
【详解】2+10×0.5
=2+5
=7(cm2)
2+8×0.5
=2+4
=6(cm2)
【点睛】此题考查的目的是理解掌握不规则图形面积的计算方法及应用。
9.26(答案在1-2范围之间浮动皆可)
【分析】数该图形所占方格数时,对于方格不是全部沾满的情况而言,若占用的一半的记作方格面积的二分之一,占用一半以上的面积是记作满格,将不满一半的方格忽略不计。
【详解】通过观察图形可知,该图形阴影的面积有26 cm。
【点睛】此题主要考查学生对图形面积估算的能力,占用的一半的记作方格面积的二分之一,占用一半以上的面积是记作满格,将不满一半的方格忽略不计。
10.7
【分析】数该图形所占方格数时,对于方格不是全部占满的情况而言,若占用的一半的记作方格面积的二分之一,占用一半以上的面积是记作满格,将不满一半的方格忽略不计。
【详解】该图形1个全部沾满,0个占方格面积的一半,6个占方格一半以上的面积,2个占不满方格一半。
1+6=7(cm2)
故答案为:7
【点睛】本题考查不规则图形的面积求法,利用数格子法来做。
11.12.5
【分析】用数格的方法即可估测出淘气出生时脚印的面积,整格的按1平方厘米计算,不足格的按半格(即0.5平方厘米)计算,再把二者相加就是淘气出生时脚印的面积大约数。
【详解】整格数:5格
5×1=5(cm2)
不足格:15格
15×0.5=7.5(cm2)
5+7.5=12.5(cm2)
即淘气出生时,脚印的面积大约是12.5cm2。
【点睛】用数方格的方法估测不规则图形的面积,分整格和不足格,不足格一律按半格计算。
12.10
【分析】看图可知,满格的一共有4格,也就是4cm2;不满一格的有12格,不满一格的都按半格算,12÷2=6(cm2);再将两部分的面积相加,可估出图中苹果的面积。
【详解】4+12÷2
=4+6
=10(cm2)
所以,图中苹果的面积约是10cm2。
(答案不唯一)
13.28平方厘米;20.5平方厘米;15.5平方厘米
【分析】根据不规则图形面积的计算方法,可以数格子,不满1格的按半格计算,根据正方形面积公式:S=边长×边长,求出1个小方格的面积,用数出的小方格个数乘面积即可。
【详解】由分析可得:
1×1=1(平方厘米)
左图:该图形由24个小方格和8个不满格的小方格组成
24×1+8×1÷2
=24+8÷2
=24+4
=28(平方厘米)
中间的图:该图形可以看作由20个小方格和1个不满格的小方格组成
20×1+1×1÷2
=20+1÷2
=20+0.5
=20.5(平方厘米)
右图:该图形由9个小方格和13个不满格的小方格组成
9×1+13×1÷2
=9+13÷2
=9+6.5
=15.5(平方厘米)
14.44平方厘米;55平方厘米;40平方厘米
17平方厘米;15平方厘米;14平方厘米;20平方厘米(答案均不唯一)
【分析】可以借助方格图数格子估算不规则图形的面积。用数格子估计不规则图形面积的方法:分别数出整数的格数和不满1格的格数;把不满1格的格数按半格计算,加上整数格,最后估算出面积。
【详解】(1)图中有32个整格,不满一格的有24格,则面积为:
(32+24÷2)×1
=(32+12)×1
=44×1
=44(平方厘米)
(2)图中有44个整格,不满一格的有22格,则面积为:
(44+22÷2)×1
=(44+11)×1
=55×1
=55(平方厘米)
(3)图中有27个整格,不满一格的有26格,则面积为:
(27+26÷2)×1
=(27+13)×1
=40×1
=40(平方厘米)
(4)图中有11个整格,不满一格的有12格,则面积为:
(11+12÷2)×1
=(11+6)×1
=17×1
=17(平方厘米)
(5)图中有7个整格,不满一格的有16格,则面积为:
(7+16÷2)×1
=(7+8)×1
=15×1
=15(平方厘米)
(6)图中有7个整格,不满一格的有14格,则面积为:
(7+14÷2)×1
=(7+7)×1
=14×1
=14(平方厘米)
(7)图中有8个整格,不满一格的有24格,则面积为:
(8+24÷2)×1
=(8+12)×1
=20×1
=20(平方厘米)
15.28平方厘米
【分析】可以把不规则图形看成一个近似的长方形,长方形的长近似7厘米,宽近似为4厘米,再用长方形的面积=长×宽,代入数据计算求解。
【详解】7×4=28(平方厘米)
答:形成的墨水渍的面积约是28平方厘米。
16.(1)等于
(2)7
(3)(4)见详解
【分析】(1)每个小方格的面积是1平方厘米,则每个小方格的边长为1厘米,再根据三角形的面积公式:S=ah÷2,长方形的面积公式:S=ab,据此分别求出图形①和图形②的面积,再进行比较即可;
(2)求不规则图形的面积,先数该图形占几个整格数,再数占多少个不满整格数,不满整格数按半格算,两个半格算一个整格,据此计算即可;
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,画出对应点,然后顺次连接各点即可;
(4)将图形②的各点先向右平移2格,再向下平移3格后,然后再顺次连接各点即可。
【详解】(1)图形①的面积:
4×1÷2+4×2÷2
=4÷2+8÷2
=2+4
=6(平方厘米)
图形②的面积:
3×2=6(平方厘米)
则图形①的面积等于图形②的面积。
(2)共有2个整格,10个半格
2×1+10÷2×1
=2+5
=7(平方厘米)
则图形③的面积约是7平方厘米。
(3)(4)如图:
17.见详解
【分析】如下图所示:
左图的面积大约等于大长方形加2个小正方形的面积即可;
右图的面积大约等于大正方形的面积加2个小正方形的面积即可。
【详解】3×2+2
=6+2
=8(平方厘米)
3×3+2×1
=9+2
=11(平方厘米)
【点睛】解答此题,要注意认真分析图形,可以将所给的图形分割成我们常见的图形,弄清图形所占的方格数,然后再计算图形的面积即可。
18.8
【分析】用数格子法算不规则图形的面积,可以把小于半格的不计,大于等于半格的计作一格,整格有4格,大于等于半格的有4格,所以钥匙总面积大约是8格,即8 cm2。
【详解】由分析可知:
4+4=8()
所以钥匙的面积大约是8 cm2。
【点睛】本题考查用数格子法算不规则图形的面积,注意:可以把小于半格的不计,大于等于半格的计作一格。
19.(1)72平方米
(2)1382.4元
【分析】(1)先数出方格的多少,计算出它的大约面积是多少;
(2)用广场的面积×4求出需要多少块瓷砖,再乘每块瓷砖的单价,即可解答。
【详解】(1)可数出72个方格,每个方格是1平方米
72×1=72(平方米)
答:它的面积大约72平方米。
(2)72×4×4.8
=288×4.8
=1382.4(元)
答:大约需要1382.4元。
【点睛】本题考查面积的估算,要仔细数出小格的数量,是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
