【广东专版】60 第十章 专题突破十二 带电粒子在交变电磁场中的运动 课件《高考快车道》2026高考物理总复习
文档属性
| 名称 | 【广东专版】60 第十章 专题突破十二 带电粒子在交变电磁场中的运动 课件《高考快车道》2026高考物理总复习 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-12-04 16:03:46 | ||
图片预览








文档简介
(共38张PPT)
第十章 磁场
专题突破十二 带电粒子在交变电磁场中的运动
细研考点·突破题型
1.交变场的常见的类型
(1)电场周期性变化,磁场不变。
(2)磁场周期性变化,电场不变。
(3)电场、磁场均周期性变化。
2.带电粒子在交变场中运动问题的基本思路
突破一 带电粒子在交变磁场中的运动
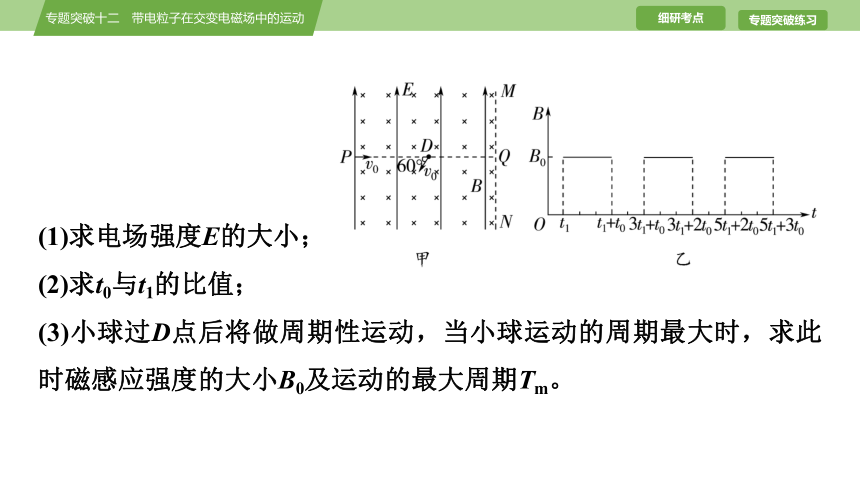
[典例1] 如图甲所示,虚线MN的左侧空间中存在竖直向上的匀强电场(上、下及左侧无边界)。一个质量为m、电荷量为q的带正电小球(视为质点),以大小为v0的水平初速度沿PQ向右做直线运动。若小球刚经过D点时(t=0),在电场所在空间叠加如图乙所示随时间周期性变化、垂直纸面向里的匀强磁场,使得小球再次通过D点时的速度方向与PQ连线成60°角。已知D、Q间的距离为(+1)L,t0小于小球在磁场中做圆周运动的周期,重力加速度大小为g。
(1)求电场强度E的大小;
(2)求t0与t1的比值;
(3)小球过D点后将做周期性运动,当小球运动的周期最大时,求此时磁感应强度的大小B0及运动的最大周期Tm。
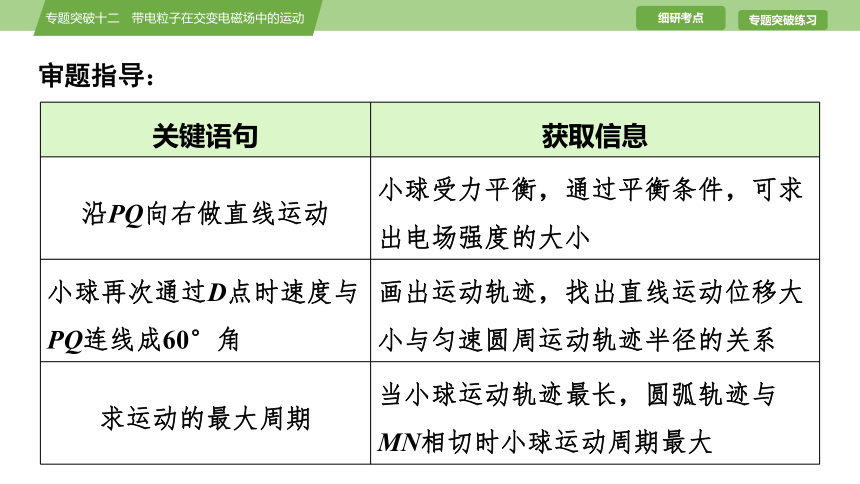
审题指导:
关键语句 获取信息
沿PQ向右做直线运动 小球受力平衡,通过平衡条件,可求出电场强度的大小
小球再次通过D点时速度与PQ连线成60°角 画出运动轨迹,找出直线运动位移大小与匀速圆周运动轨迹半径的关系
求运动的最大周期 当小球运动轨迹最长,圆弧轨迹与MN相切时小球运动周期最大
[解析] (1)小球沿PQ向右做直线运动,受力平衡,则mg=Eq,解得E=。
(2)小球能再次通过D点,其运动轨迹应
如图(a)所示。
设小球做匀速圆周运动的轨迹半径为r,
则由几何关系有s=
又知s=v0t1
圆弧轨迹所对的圆心角θ=2π-=π,则t0=,联立解得=π。
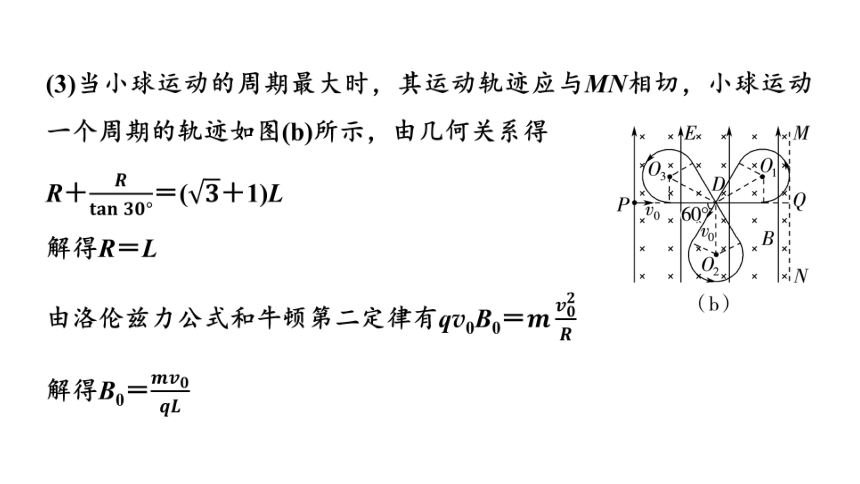
(3)当小球运动的周期最大时,其运动轨迹应与MN相切,小球运动一个周期的轨迹如图(b)所示,由几何关系得
R+=(+1)L
解得R=L
由洛伦兹力公式和牛顿第二定律有qv0B0=
解得B0=
小球在一个周期内运动的路程
s1=3××2πR+6×=(4π+6)L
故Tm==。
[答案] (1) (2)π (3)
突破二 带电粒子在交变电磁场中的运动
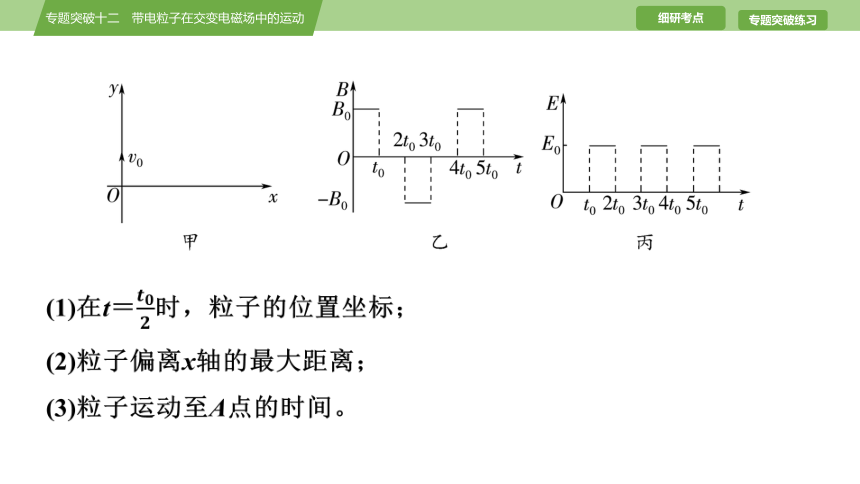
[典例2] (2025·广东惠州模拟)如图甲所示,在xOy平面内存在磁场和电场,磁感应强度和电场强度大小随时间周期性变化,B的变化周期为4t0,E的变化周期为2t0,变化规律分别如图乙和图丙所示。在t=0时刻从O点发射一带负电的粒子(不计重力),初速度大小为v0,方向沿y轴正方向,在x轴上有一点A(图中未标出),坐标为。若规定垂直纸面向里为磁感应强度的正方向,y轴正方向为电场强度的正方向,v0、t0、B0为已知量,磁感应强度与电场强度的大小满足=,粒子的比荷满足=。求:
(1)在t=时,粒子的位置坐标;
(2)粒子偏离x轴的最大距离;
(3)粒子运动至A点的时间。
[解析] (1)在0~t0时间内,粒子做匀速圆周运动,根据洛伦兹力提供向心力可得
qv0B0=mr1=
解得T=2t0,r1==
则粒子在时间内转过的圆心角α=
所以在t=时,粒子的位置坐标为。
(2)在t0~2t0时间内,设粒子经电场加速后的速度为v,粒子的运动轨迹如图所示。
则v=v0+t0=2v0
运动的位移x=t0=v0t0
在2t0~3t0时间内粒子做匀速圆周运动
半径r2=2r1=
故粒子偏离x轴的最大距离
h=x+r2=v0t0+。
(3)粒子在xOy平面内做周期性运动的运动周期为4t0,故粒子在一个周期内向右运动的距离
d=2r1+2r2=
A、O间的距离为=8d
所以,粒子运动至A点的时间t=32t0。
[答案] (1) (2)v0t0+ (3)32t0
[典例3] (2025·广东珠海模拟)如图甲所示,在xOy平面内存在均匀、大小随时间周期性变化的磁场和电场,变化规律分别如图乙、丙所示(规定垂直纸面向里为磁感应强度的正方向、沿y轴正方向电场强度为正)。在t=0时刻由原点O发射初速度大小为v0、方向沿y轴正方向的带负电粒子。已知v0、t0、B0,粒子的比荷为,不计粒子的重力。求:
(1)t=t0时,粒子的位置坐标;
(2)若t=5t0时粒子回到原点,0~5t0时间内粒子距x轴的最大距离;
(3)若粒子能够回到原点,满足条件的所有E0值。
[解析] (1)粒子在0~t0时间内沿顺时针方向做匀速圆周运动,有qv0B0=,T=
解得r1=,T=
又粒子的比荷=
解得r1=,T=2t0
故t=t0时,粒子的位置坐标为。
(2)粒子在t=5t0时回到原点,运动轨迹如图(a)所示。由r2=2r1,r1=,r2=,解得v2=2v0
则在0~5t0时间内粒子距x轴的最大距离hm=t0+r2=v0t0。
(3)如图(b)所示,设带电粒子在x轴下方做圆周运动的轨迹半径为,由几何关系可知,要使粒子能够回到原点,则必须满足
n(2r′2-2r1)=2r1(n=1,2,3,…)
其中r′2=
解得v=v0(n=1,2,3,…)
又v=v0+t0
解得E0=(n=1,2,3,…)。
[答案] (1) (2)v0t0
(3)(n=1,2,3,…)
专题突破练习(十二) 带电粒子在交变电磁场中的运动
1.如图所示,一个质量为m、电荷量为+q的带电粒子,不计重力,在a点以某一初速度水平向左射入磁场区域Ⅰ,沿曲线abcd运动,ab、bc、cd都是半径为R的圆弧,粒子在每段圆弧上运动的时间都为t。规定垂直于纸面向外的磁感应强度为正,则磁场
区域Ⅰ、Ⅱ、Ⅲ三部分的磁感应强度B随x变化
的关系可能是( )
A B
C D
√
C [由左手定则可判断出磁感应强度B在区域Ⅰ、Ⅱ、Ⅲ内的方向分别为向外、向里和向外,在三个区域中均运动圆周,故t=,由于T=,求得B=,选项C正确。]
2.如图(a)所示的xOy平面处于变化的匀强电场和匀强磁场中,电场强度E和磁感应强度B随时间做周期性变化的图像如图(b)所示,y轴正方向为E的正方向,垂直于纸面向里为B的正方向,t=0时刻,带负电粒子P(重力不计)由原点O以速度v0沿y轴正方向射出,它恰能沿一定轨道做周期性运动。v0、E0和t0为已知量,图(b)中=,在0~t0时间内粒子P第一次离x轴最远时的坐标为。求:
(1)粒子P的比荷;
(2)t=2t0时刻粒子P的位置坐标;
(3)带电粒子在运动中距离原点O的最远距离L。
[解析] (1)0~t0时间内粒子P在匀强磁场中做匀速圆周运动,当粒子所在位置的纵、横坐标相等时,粒子在磁场中恰好经过圆周,所以粒子P第一次离x轴的最远距离等于轨道半径R,即
R= ①
又qv0B0= ②
代入=
解得=。 ③
(2)设粒子P在磁场中运动的周期为T,则
T= ④
联立①④式解得T=4t0 ⑤
即粒子P做圆周运动后磁场变为电场,粒子以速度v0垂直电场方向进入电场后做类平抛运动,设t0~2t0时间内水平位移和竖直位移分别为x1、y1,则
x1=v0t0= ⑥
y1= ⑦
其中加速度a= ⑧
由③⑦⑧式解得y1==R
因此t=2t0时刻粒子P的位置坐标为
,如图中的b点所示。
(3)分析知,粒子P在2t0~3t0时间内,电场力产生的加速度方向沿y轴正方向,由对称关系知,在3t0时刻速度方向为x轴正方向,水平位移x2=x1=v0t0;在3t0~5t0时间内粒子P沿逆时针方向做匀速圆周运动,往复运动轨迹如图所示,由图可知,带电粒子在运动中距原点O的最远距离L即O、d间的距离L=2R+2x1
解得L=v0t0。
[答案] (1) (2) (3)v0t0
3.(2025·广东汕头检测)如图甲所示,建立xOy平面直角坐标系,两平行极板P、Q垂直于y轴且关于x轴对称,极板长度和板间距均为l,第一、四象限有足够大的匀强磁场B,方向垂直于xOy平面向里。位于极板左侧的粒子源沿x轴向右接连发射质量为m、电荷量为+q、速度相同、重力不计的带电粒子,在0~3t0时间内两板间加上如图乙所示的电压(不考虑边缘效应的影响),规定沿y轴负方向为电场正方向。已知t=0时刻进入两板间的带电粒子恰好在t0时刻经极板边缘射入磁场,上述m、q、l、t0、B为已知量。(不考虑粒子间的相互影响及返回板间的情况)
(1)求电压U0的大小;
(2)求t0时刻进入两板间的带电粒子在磁场中做圆周运动的半径;
(3)何时进入两板间的带电粒子在磁场中的运动时间最短?求此最短时间。
[解析] (1)t=0时刻进入两极板的带电粒子在电场中做类平抛运动,t0时刻刚好从极板边缘射出,则粒子在y轴负方向偏移的距离为l
竖直方向上,根据运动学公式有l=
由牛顿第二定律有q=ma
联立解得U0=。
(2)t0时刻进入两极板间的带电粒子,在两极板间,前t0时间在电场中偏转,后t0时间两极板间没有电场,带电粒子做匀速直线运动,带电粒子沿x轴方向的分速度大小为v0=
带电粒子离开电场时沿y轴负方向的分速度大小为
vy=a·t0
带电粒子离开电场时的速度大小为v=
设带电粒子进入磁场做匀速圆周运动的半径为R,则有qvB=m
联立解得R=。
(3)带电粒子在磁场中的运动轨迹所对的圆心角越小,则在磁场中运动的时间越短,经分析可知,2t0时刻进入两极板间的带电粒子在磁场中运动时间最短,设此种情况下粒子离开电场时速度方向与y轴正方向的夹角为α,如图所示。带电粒子离开电场时沿y轴正方向的分速度为v′y=at0
根据几何关系有tan α=
联立解得α=
则粒子在磁场中的运动轨迹所对的圆心角为
2α=
所求最短时间为tmin=T
带电粒子在磁场中运动的周期为T=
解得tmin=。
[答案] (2) (3)2t0
谢 谢 !
第十章 磁场
专题突破十二 带电粒子在交变电磁场中的运动
细研考点·突破题型
1.交变场的常见的类型
(1)电场周期性变化,磁场不变。
(2)磁场周期性变化,电场不变。
(3)电场、磁场均周期性变化。
2.带电粒子在交变场中运动问题的基本思路
突破一 带电粒子在交变磁场中的运动
[典例1] 如图甲所示,虚线MN的左侧空间中存在竖直向上的匀强电场(上、下及左侧无边界)。一个质量为m、电荷量为q的带正电小球(视为质点),以大小为v0的水平初速度沿PQ向右做直线运动。若小球刚经过D点时(t=0),在电场所在空间叠加如图乙所示随时间周期性变化、垂直纸面向里的匀强磁场,使得小球再次通过D点时的速度方向与PQ连线成60°角。已知D、Q间的距离为(+1)L,t0小于小球在磁场中做圆周运动的周期,重力加速度大小为g。
(1)求电场强度E的大小;
(2)求t0与t1的比值;
(3)小球过D点后将做周期性运动,当小球运动的周期最大时,求此时磁感应强度的大小B0及运动的最大周期Tm。
审题指导:
关键语句 获取信息
沿PQ向右做直线运动 小球受力平衡,通过平衡条件,可求出电场强度的大小
小球再次通过D点时速度与PQ连线成60°角 画出运动轨迹,找出直线运动位移大小与匀速圆周运动轨迹半径的关系
求运动的最大周期 当小球运动轨迹最长,圆弧轨迹与MN相切时小球运动周期最大
[解析] (1)小球沿PQ向右做直线运动,受力平衡,则mg=Eq,解得E=。
(2)小球能再次通过D点,其运动轨迹应
如图(a)所示。
设小球做匀速圆周运动的轨迹半径为r,
则由几何关系有s=
又知s=v0t1
圆弧轨迹所对的圆心角θ=2π-=π,则t0=,联立解得=π。
(3)当小球运动的周期最大时,其运动轨迹应与MN相切,小球运动一个周期的轨迹如图(b)所示,由几何关系得
R+=(+1)L
解得R=L
由洛伦兹力公式和牛顿第二定律有qv0B0=
解得B0=
小球在一个周期内运动的路程
s1=3××2πR+6×=(4π+6)L
故Tm==。
[答案] (1) (2)π (3)
突破二 带电粒子在交变电磁场中的运动
[典例2] (2025·广东惠州模拟)如图甲所示,在xOy平面内存在磁场和电场,磁感应强度和电场强度大小随时间周期性变化,B的变化周期为4t0,E的变化周期为2t0,变化规律分别如图乙和图丙所示。在t=0时刻从O点发射一带负电的粒子(不计重力),初速度大小为v0,方向沿y轴正方向,在x轴上有一点A(图中未标出),坐标为。若规定垂直纸面向里为磁感应强度的正方向,y轴正方向为电场强度的正方向,v0、t0、B0为已知量,磁感应强度与电场强度的大小满足=,粒子的比荷满足=。求:
(1)在t=时,粒子的位置坐标;
(2)粒子偏离x轴的最大距离;
(3)粒子运动至A点的时间。
[解析] (1)在0~t0时间内,粒子做匀速圆周运动,根据洛伦兹力提供向心力可得
qv0B0=mr1=
解得T=2t0,r1==
则粒子在时间内转过的圆心角α=
所以在t=时,粒子的位置坐标为。
(2)在t0~2t0时间内,设粒子经电场加速后的速度为v,粒子的运动轨迹如图所示。
则v=v0+t0=2v0
运动的位移x=t0=v0t0
在2t0~3t0时间内粒子做匀速圆周运动
半径r2=2r1=
故粒子偏离x轴的最大距离
h=x+r2=v0t0+。
(3)粒子在xOy平面内做周期性运动的运动周期为4t0,故粒子在一个周期内向右运动的距离
d=2r1+2r2=
A、O间的距离为=8d
所以,粒子运动至A点的时间t=32t0。
[答案] (1) (2)v0t0+ (3)32t0
[典例3] (2025·广东珠海模拟)如图甲所示,在xOy平面内存在均匀、大小随时间周期性变化的磁场和电场,变化规律分别如图乙、丙所示(规定垂直纸面向里为磁感应强度的正方向、沿y轴正方向电场强度为正)。在t=0时刻由原点O发射初速度大小为v0、方向沿y轴正方向的带负电粒子。已知v0、t0、B0,粒子的比荷为,不计粒子的重力。求:
(1)t=t0时,粒子的位置坐标;
(2)若t=5t0时粒子回到原点,0~5t0时间内粒子距x轴的最大距离;
(3)若粒子能够回到原点,满足条件的所有E0值。
[解析] (1)粒子在0~t0时间内沿顺时针方向做匀速圆周运动,有qv0B0=,T=
解得r1=,T=
又粒子的比荷=
解得r1=,T=2t0
故t=t0时,粒子的位置坐标为。
(2)粒子在t=5t0时回到原点,运动轨迹如图(a)所示。由r2=2r1,r1=,r2=,解得v2=2v0
则在0~5t0时间内粒子距x轴的最大距离hm=t0+r2=v0t0。
(3)如图(b)所示,设带电粒子在x轴下方做圆周运动的轨迹半径为,由几何关系可知,要使粒子能够回到原点,则必须满足
n(2r′2-2r1)=2r1(n=1,2,3,…)
其中r′2=
解得v=v0(n=1,2,3,…)
又v=v0+t0
解得E0=(n=1,2,3,…)。
[答案] (1) (2)v0t0
(3)(n=1,2,3,…)
专题突破练习(十二) 带电粒子在交变电磁场中的运动
1.如图所示,一个质量为m、电荷量为+q的带电粒子,不计重力,在a点以某一初速度水平向左射入磁场区域Ⅰ,沿曲线abcd运动,ab、bc、cd都是半径为R的圆弧,粒子在每段圆弧上运动的时间都为t。规定垂直于纸面向外的磁感应强度为正,则磁场
区域Ⅰ、Ⅱ、Ⅲ三部分的磁感应强度B随x变化
的关系可能是( )
A B
C D
√
C [由左手定则可判断出磁感应强度B在区域Ⅰ、Ⅱ、Ⅲ内的方向分别为向外、向里和向外,在三个区域中均运动圆周,故t=,由于T=,求得B=,选项C正确。]
2.如图(a)所示的xOy平面处于变化的匀强电场和匀强磁场中,电场强度E和磁感应强度B随时间做周期性变化的图像如图(b)所示,y轴正方向为E的正方向,垂直于纸面向里为B的正方向,t=0时刻,带负电粒子P(重力不计)由原点O以速度v0沿y轴正方向射出,它恰能沿一定轨道做周期性运动。v0、E0和t0为已知量,图(b)中=,在0~t0时间内粒子P第一次离x轴最远时的坐标为。求:
(1)粒子P的比荷;
(2)t=2t0时刻粒子P的位置坐标;
(3)带电粒子在运动中距离原点O的最远距离L。
[解析] (1)0~t0时间内粒子P在匀强磁场中做匀速圆周运动,当粒子所在位置的纵、横坐标相等时,粒子在磁场中恰好经过圆周,所以粒子P第一次离x轴的最远距离等于轨道半径R,即
R= ①
又qv0B0= ②
代入=
解得=。 ③
(2)设粒子P在磁场中运动的周期为T,则
T= ④
联立①④式解得T=4t0 ⑤
即粒子P做圆周运动后磁场变为电场,粒子以速度v0垂直电场方向进入电场后做类平抛运动,设t0~2t0时间内水平位移和竖直位移分别为x1、y1,则
x1=v0t0= ⑥
y1= ⑦
其中加速度a= ⑧
由③⑦⑧式解得y1==R
因此t=2t0时刻粒子P的位置坐标为
,如图中的b点所示。
(3)分析知,粒子P在2t0~3t0时间内,电场力产生的加速度方向沿y轴正方向,由对称关系知,在3t0时刻速度方向为x轴正方向,水平位移x2=x1=v0t0;在3t0~5t0时间内粒子P沿逆时针方向做匀速圆周运动,往复运动轨迹如图所示,由图可知,带电粒子在运动中距原点O的最远距离L即O、d间的距离L=2R+2x1
解得L=v0t0。
[答案] (1) (2) (3)v0t0
3.(2025·广东汕头检测)如图甲所示,建立xOy平面直角坐标系,两平行极板P、Q垂直于y轴且关于x轴对称,极板长度和板间距均为l,第一、四象限有足够大的匀强磁场B,方向垂直于xOy平面向里。位于极板左侧的粒子源沿x轴向右接连发射质量为m、电荷量为+q、速度相同、重力不计的带电粒子,在0~3t0时间内两板间加上如图乙所示的电压(不考虑边缘效应的影响),规定沿y轴负方向为电场正方向。已知t=0时刻进入两板间的带电粒子恰好在t0时刻经极板边缘射入磁场,上述m、q、l、t0、B为已知量。(不考虑粒子间的相互影响及返回板间的情况)
(1)求电压U0的大小;
(2)求t0时刻进入两板间的带电粒子在磁场中做圆周运动的半径;
(3)何时进入两板间的带电粒子在磁场中的运动时间最短?求此最短时间。
[解析] (1)t=0时刻进入两极板的带电粒子在电场中做类平抛运动,t0时刻刚好从极板边缘射出,则粒子在y轴负方向偏移的距离为l
竖直方向上,根据运动学公式有l=
由牛顿第二定律有q=ma
联立解得U0=。
(2)t0时刻进入两极板间的带电粒子,在两极板间,前t0时间在电场中偏转,后t0时间两极板间没有电场,带电粒子做匀速直线运动,带电粒子沿x轴方向的分速度大小为v0=
带电粒子离开电场时沿y轴负方向的分速度大小为
vy=a·t0
带电粒子离开电场时的速度大小为v=
设带电粒子进入磁场做匀速圆周运动的半径为R,则有qvB=m
联立解得R=。
(3)带电粒子在磁场中的运动轨迹所对的圆心角越小,则在磁场中运动的时间越短,经分析可知,2t0时刻进入两极板间的带电粒子在磁场中运动时间最短,设此种情况下粒子离开电场时速度方向与y轴正方向的夹角为α,如图所示。带电粒子离开电场时沿y轴正方向的分速度为v′y=at0
根据几何关系有tan α=
联立解得α=
则粒子在磁场中的运动轨迹所对的圆心角为
2α=
所求最短时间为tmin=T
带电粒子在磁场中运动的周期为T=
解得tmin=。
[答案] (2) (3)2t0
谢 谢 !
同课章节目录
