甘肃省武威第二十中学2024-2025学年下学期期末考试七年级数学试卷(含答案)
文档属性
| 名称 | 甘肃省武威第二十中学2024-2025学年下学期期末考试七年级数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 644.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-08 00:00:00 | ||
图片预览




文档简介
2024-2025学年下学期期末考试七年级数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列四个实数中,最小的数是( )
A. B. C. D.
2.方程的正整数解有( )个
A.1 B.2 C.3 D.4
3.的平方根是( )
A. B.4 C.2 D.
4.不等式组的解集在数轴上表示为( )
A. B. C. D.
5.如图,是锐角,点从点出发沿方向运动,连接.若,点到所在直线的距离为3,则的长度不可能为( )
A.5 B.4 C.3 D.2
6.为了调查不同品牌的衬衣销售情况,某校数学兴趣小组统计了A,B两款衬衣一周的销量,下图是两款衬衣一周的销量变化趋势图,则下列说法正确的是( )
A.甲款衬衣的销量比乙款衬衣销量稳定
B.乙款衬衣的销量平均数高于甲款衬衣
C.甲款衬衣与乙款衬衣销量的变化趋势相同
D.甲款衬衣的销量比乙款衬衣的销量好
7.如图所示,有一个正方体集装箱,体积为,现准备将其改造(形状仍为正方体),以便盛放更多的货物,为使其体积达到,棱长应变为原来的( )
A.倍 B.倍 C. D.
8.数经历了从自然数到有理数,到实数,再到复数的发展过程,数学中把形如a+bi(a,b为实数)的数叫做复数,用z=a+bi表示,任何一个复数z=a+bi在平面直角坐标系中都可以用有序数对Z(a,b)表示,如:z=1+2i表示为Z(1,2),则z=2﹣i可表示为( )
A.Z(2,0) B.Z(2,﹣1) C.Z(2,1) D.Z(﹣1,2)
9.如图,直线,点是直线与直线中间一点,点、分别在直线、上,连接并延长至点,连接,过点作,点是直线上方一点,连接,.已知,,则、与之间的数量关系为( )
A. B.
C. D.
10.已知实数a,b满足,且,,则的取值范围是( )
A. B. C. D.
二、填空题
11.若,则 (填或).
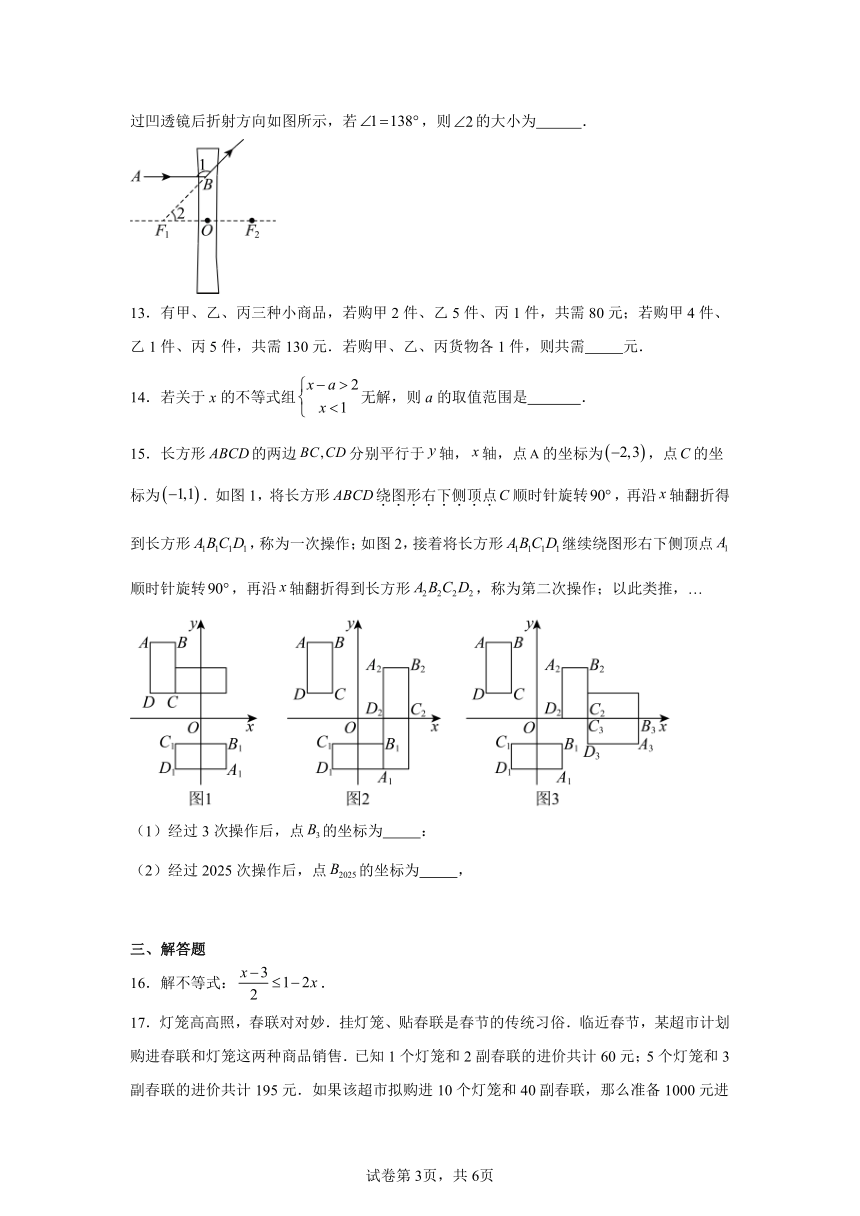
12.一束平行于主光轴的光线射向凹透镜.点均为凹透镜的焦点.光线经过凹透镜后折射方向如图所示,若,则的大小为 .
13.有甲、乙、丙三种小商品,若购甲2件、乙5件、丙1件,共需80元;若购甲4件、乙1件、丙5件,共需130元.若购甲、乙、丙货物各1件,则共需 元.
14.若关于x的不等式组无解,则a的取值范围是 .
15.长方形的两边分别平行于轴,轴,点的坐标为,点的坐标为.如图1,将长方形绕图形右下侧顶点顺时针旋转,再沿轴翻折得到长方形,称为一次操作;如图2,接着将长方形继续绕图形右下侧顶点顺时针旋转,再沿轴翻折得到长方形,称为第二次操作;以此类推,…
(1)经过3次操作后,点的坐标为 :
(2)经过2025次操作后,点的坐标为 ,
三、解答题
16.解不等式:.
17.灯笼高高照,春联对对妙.挂灯笼、贴春联是春节的传统习俗.临近春节,某超市计划购进春联和灯笼这两种商品销售.已知1个灯笼和2副春联的进价共计60元;5个灯笼和3副春联的进价共计195元.如果该超市拟购进10个灯笼和40副春联,那么准备1000元进货够了吗
18.如图为的方形网格,每个小正方形的边长均为1个单位长度.有线段(端点、均在小正方形的顶点上),将线段平移得到线段,规定点移至点的位置,点移至点的位置(、均在小正方形的顶点上),设平移过程中线段扫过的面积为.
(1)在图1方形网格建立并画出恰当的平面直角坐标系,使得点坐标为,点坐标为,并写出点的坐标(_____,_____);
(2)在图1中画出线段,并直接写出相对应的的值;
(3)若,请在图2中画出线段.(注:只需画出符合要求的一种情况即可)
19.点为平面直角坐标系内一点.
(1)若点在轴上,则的值为_____;
(2)若点在第二象限,且点到两坐标轴的距离之和为9,求点的坐标.
20.对于未知数为,的二元一次方程组,如果方程组的解,满足,我们就说方程组的解与具有“邻好关系”.
(1)方程组的解与是否具有“邻好关系”?说明你的理由;
(2)若方程组的解与具有“邻好关系”,求的值.
21.2024-2025年AI大模型井喷式发展,某校学生为了解全校学生对AI大模型的使用情况开展了相关抽样调查.同学们对此次调查设计了调查问卷,发放了200份问卷并全部回收,对回收的问卷做了归纳统计,相关信息如下:
AI大模型调查问卷请根据实际情况填写,每空填写一个.问题1:你平时学习生活中会使用AI大模型吗 (填会或不会) 问题1中回答“会”的请继续回答下面问题: 问题2:你平时学习生活中使用最多的AI大模型是. (A)豆包 (B)DeepSeek (C)Kimi (D)通义千问 (E)其他问题 3:你使用AI大模型主要是用于以下哪个方面 (A)辅助学习 (B)查找信息 (C)休闲娱乐 (D)其他
根据以上信息.解答下列问题:
(1)本次调查的200人中使用最多的AI大模型为“豆包”的有多少人?
(2)全校共有2000名学生,根据统计信息,估计该校使用最多的AI大模型为“通义千问”的学生人数.
22.如图,已知,于点,于点.
(1)求证:;
(2)若,,求的度数.
23.学校开展“生活中的数学问题”学习活动,某小组选择“汽车轮胎换位问题”为研究方向.
【问题背景】大多数小汽车是前轮驱动和转向的,所以前轮的磨损程度比后轮严重.如果前轮报废,换上新轮胎,而后轮继续使用原来的轮胎,那么汽车行驶的安全性和乘坐的舒适性都将大打折扣;如果同时更换前后轮的轮胎,用车成本又会提高.为了解决这个问题,一般的汽车使用手册上都有定期给前后轮的轮胎换位的建议.
【数据信息】
1.汽车前轮一对轮胎一般应在汽车行驶达到6万公里时报废,而后轮一对轮胎应在汽车行驶达到8万公里时报废;
2.轮胎的磨损量汽车行驶的单位路程的磨损量汽车行驶的路程.
【问题解决】
(1)若每对新轮胎报废时的总磨损量为1,则安装在前轮的一对轮胎每行驶1万公里的磨损量为_____,安装在后轮的一对轮胎每行驶1万公里的磨损量为_____;
(2)如果在轮胎的使用寿命内只交换一次前、后轮轮胎,那么应在汽车行驶里程达到多少万公里时,交换前、后轮轮胎,能使汽车的前后两对轮胎同时报废 (结果保留小数点后两位)
注:“同时报废”指的是前后两对轮胎的总磨损量均为1.
试卷第1页,共3页
试卷第1页,共3页
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A B D C D D A B B B
11.
12./度
13.35
14.
15.
16.
17.准备1000元够
18.(1)解:把点坐标为,向下平移2个单位即可得到原点,建立坐标系如下:
故点A向右平移1个单位,再向上平移1个单位得到点M,
由把点坐标为,向右平移1个单位,再向上平移1个单位得到点N,
故,
故答案为:1,3;
(2)解:根据平移,画图如下:
则即为所求;
且;
(3)解:,故将点A向右平移4个单位即可,画图如下:
19.(1)解:点P在x轴上,
,
.
故答案为:0;
(2)解:在第二象限,
点到x轴的距离为,到轴的距离为,
点到两坐标轴的距离之和为9,
,
,代入得点的坐标为.
20.(1)解:,
由②得:,即满足.
∴方程组的解,具有“邻好关系”;
(2)解:方程组,
①-②得:,即.
∵方程组的解,具有“邻好关系”,
∴,即,
∴或.
21.解:(1)(人),
答:本次调查的200人中使用最多的AI大模型为“豆包”的有45人.
(2)由图可知:Kimi所占百分比为,
则通义千问所占百比分为:,
(人)
答:使用最多的AI大模型为“通义千问”的学生人数为90人.
22.(1)证明:∵于D,于F.
∴,
∴.
∴.
∵,
∴.
∴.
(2)解:,,
又,
,
解得.
.
又,
∴
.
23.(1)解:已知汽车前轮一对轮胎行驶6万公里报废,且每对新轮胎报废时总磨损量为1,那么安装在前轮的一对轮胎每行驶1万公里的磨损量为;
同理,后轮一对轮胎行驶8万公里报废,所以安装在后轮的一对轮胎每行驶1万公里
的磨损量为;
故答案为:;;
(2)解:设行驶x万公里时前后轮交换,然后再行驶y万公里两对轮胎同时报废.
∵前轮剩余的磨损量为,后轮剩余的磨损量为,
∴由题意可得,
消元得.
解得:(万公里).
即应在汽车行驶里程达到3.43万公里时,交换前、后轮轮胎,能使汽车的两对轮胎同时报废.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列四个实数中,最小的数是( )
A. B. C. D.
2.方程的正整数解有( )个
A.1 B.2 C.3 D.4
3.的平方根是( )
A. B.4 C.2 D.
4.不等式组的解集在数轴上表示为( )
A. B. C. D.
5.如图,是锐角,点从点出发沿方向运动,连接.若,点到所在直线的距离为3,则的长度不可能为( )
A.5 B.4 C.3 D.2
6.为了调查不同品牌的衬衣销售情况,某校数学兴趣小组统计了A,B两款衬衣一周的销量,下图是两款衬衣一周的销量变化趋势图,则下列说法正确的是( )
A.甲款衬衣的销量比乙款衬衣销量稳定
B.乙款衬衣的销量平均数高于甲款衬衣
C.甲款衬衣与乙款衬衣销量的变化趋势相同
D.甲款衬衣的销量比乙款衬衣的销量好
7.如图所示,有一个正方体集装箱,体积为,现准备将其改造(形状仍为正方体),以便盛放更多的货物,为使其体积达到,棱长应变为原来的( )
A.倍 B.倍 C. D.
8.数经历了从自然数到有理数,到实数,再到复数的发展过程,数学中把形如a+bi(a,b为实数)的数叫做复数,用z=a+bi表示,任何一个复数z=a+bi在平面直角坐标系中都可以用有序数对Z(a,b)表示,如:z=1+2i表示为Z(1,2),则z=2﹣i可表示为( )
A.Z(2,0) B.Z(2,﹣1) C.Z(2,1) D.Z(﹣1,2)
9.如图,直线,点是直线与直线中间一点,点、分别在直线、上,连接并延长至点,连接,过点作,点是直线上方一点,连接,.已知,,则、与之间的数量关系为( )
A. B.
C. D.
10.已知实数a,b满足,且,,则的取值范围是( )
A. B. C. D.
二、填空题
11.若,则 (填或).
12.一束平行于主光轴的光线射向凹透镜.点均为凹透镜的焦点.光线经过凹透镜后折射方向如图所示,若,则的大小为 .
13.有甲、乙、丙三种小商品,若购甲2件、乙5件、丙1件,共需80元;若购甲4件、乙1件、丙5件,共需130元.若购甲、乙、丙货物各1件,则共需 元.
14.若关于x的不等式组无解,则a的取值范围是 .
15.长方形的两边分别平行于轴,轴,点的坐标为,点的坐标为.如图1,将长方形绕图形右下侧顶点顺时针旋转,再沿轴翻折得到长方形,称为一次操作;如图2,接着将长方形继续绕图形右下侧顶点顺时针旋转,再沿轴翻折得到长方形,称为第二次操作;以此类推,…
(1)经过3次操作后,点的坐标为 :
(2)经过2025次操作后,点的坐标为 ,
三、解答题
16.解不等式:.
17.灯笼高高照,春联对对妙.挂灯笼、贴春联是春节的传统习俗.临近春节,某超市计划购进春联和灯笼这两种商品销售.已知1个灯笼和2副春联的进价共计60元;5个灯笼和3副春联的进价共计195元.如果该超市拟购进10个灯笼和40副春联,那么准备1000元进货够了吗
18.如图为的方形网格,每个小正方形的边长均为1个单位长度.有线段(端点、均在小正方形的顶点上),将线段平移得到线段,规定点移至点的位置,点移至点的位置(、均在小正方形的顶点上),设平移过程中线段扫过的面积为.
(1)在图1方形网格建立并画出恰当的平面直角坐标系,使得点坐标为,点坐标为,并写出点的坐标(_____,_____);
(2)在图1中画出线段,并直接写出相对应的的值;
(3)若,请在图2中画出线段.(注:只需画出符合要求的一种情况即可)
19.点为平面直角坐标系内一点.
(1)若点在轴上,则的值为_____;
(2)若点在第二象限,且点到两坐标轴的距离之和为9,求点的坐标.
20.对于未知数为,的二元一次方程组,如果方程组的解,满足,我们就说方程组的解与具有“邻好关系”.
(1)方程组的解与是否具有“邻好关系”?说明你的理由;
(2)若方程组的解与具有“邻好关系”,求的值.
21.2024-2025年AI大模型井喷式发展,某校学生为了解全校学生对AI大模型的使用情况开展了相关抽样调查.同学们对此次调查设计了调查问卷,发放了200份问卷并全部回收,对回收的问卷做了归纳统计,相关信息如下:
AI大模型调查问卷请根据实际情况填写,每空填写一个.问题1:你平时学习生活中会使用AI大模型吗 (填会或不会) 问题1中回答“会”的请继续回答下面问题: 问题2:你平时学习生活中使用最多的AI大模型是. (A)豆包 (B)DeepSeek (C)Kimi (D)通义千问 (E)其他问题 3:你使用AI大模型主要是用于以下哪个方面 (A)辅助学习 (B)查找信息 (C)休闲娱乐 (D)其他
根据以上信息.解答下列问题:
(1)本次调查的200人中使用最多的AI大模型为“豆包”的有多少人?
(2)全校共有2000名学生,根据统计信息,估计该校使用最多的AI大模型为“通义千问”的学生人数.
22.如图,已知,于点,于点.
(1)求证:;
(2)若,,求的度数.
23.学校开展“生活中的数学问题”学习活动,某小组选择“汽车轮胎换位问题”为研究方向.
【问题背景】大多数小汽车是前轮驱动和转向的,所以前轮的磨损程度比后轮严重.如果前轮报废,换上新轮胎,而后轮继续使用原来的轮胎,那么汽车行驶的安全性和乘坐的舒适性都将大打折扣;如果同时更换前后轮的轮胎,用车成本又会提高.为了解决这个问题,一般的汽车使用手册上都有定期给前后轮的轮胎换位的建议.
【数据信息】
1.汽车前轮一对轮胎一般应在汽车行驶达到6万公里时报废,而后轮一对轮胎应在汽车行驶达到8万公里时报废;
2.轮胎的磨损量汽车行驶的单位路程的磨损量汽车行驶的路程.
【问题解决】
(1)若每对新轮胎报废时的总磨损量为1,则安装在前轮的一对轮胎每行驶1万公里的磨损量为_____,安装在后轮的一对轮胎每行驶1万公里的磨损量为_____;
(2)如果在轮胎的使用寿命内只交换一次前、后轮轮胎,那么应在汽车行驶里程达到多少万公里时,交换前、后轮轮胎,能使汽车的前后两对轮胎同时报废 (结果保留小数点后两位)
注:“同时报废”指的是前后两对轮胎的总磨损量均为1.
试卷第1页,共3页
试卷第1页,共3页
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A B D C D D A B B B
11.
12./度
13.35
14.
15.
16.
17.准备1000元够
18.(1)解:把点坐标为,向下平移2个单位即可得到原点,建立坐标系如下:
故点A向右平移1个单位,再向上平移1个单位得到点M,
由把点坐标为,向右平移1个单位,再向上平移1个单位得到点N,
故,
故答案为:1,3;
(2)解:根据平移,画图如下:
则即为所求;
且;
(3)解:,故将点A向右平移4个单位即可,画图如下:
19.(1)解:点P在x轴上,
,
.
故答案为:0;
(2)解:在第二象限,
点到x轴的距离为,到轴的距离为,
点到两坐标轴的距离之和为9,
,
,代入得点的坐标为.
20.(1)解:,
由②得:,即满足.
∴方程组的解,具有“邻好关系”;
(2)解:方程组,
①-②得:,即.
∵方程组的解,具有“邻好关系”,
∴,即,
∴或.
21.解:(1)(人),
答:本次调查的200人中使用最多的AI大模型为“豆包”的有45人.
(2)由图可知:Kimi所占百分比为,
则通义千问所占百比分为:,
(人)
答:使用最多的AI大模型为“通义千问”的学生人数为90人.
22.(1)证明:∵于D,于F.
∴,
∴.
∴.
∵,
∴.
∴.
(2)解:,,
又,
,
解得.
.
又,
∴
.
23.(1)解:已知汽车前轮一对轮胎行驶6万公里报废,且每对新轮胎报废时总磨损量为1,那么安装在前轮的一对轮胎每行驶1万公里的磨损量为;
同理,后轮一对轮胎行驶8万公里报废,所以安装在后轮的一对轮胎每行驶1万公里
的磨损量为;
故答案为:;;
(2)解:设行驶x万公里时前后轮交换,然后再行驶y万公里两对轮胎同时报废.
∵前轮剩余的磨损量为,后轮剩余的磨损量为,
∴由题意可得,
消元得.
解得:(万公里).
即应在汽车行驶里程达到3.43万公里时,交换前、后轮轮胎,能使汽车的两对轮胎同时报废.
答案第1页,共2页
答案第1页,共2页
同课章节目录
