13.3三角形的内角与外角 同步练习(含解析) 2025-2026学年人教版数学八年级上册
文档属性
| 名称 | 13.3三角形的内角与外角 同步练习(含解析) 2025-2026学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 889.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 19:01:38 | ||
图片预览



文档简介
13.3三角形的内角与外角 同步练习
学校:___________姓名:___________班级:___________学号:___________
一、单选题
1.如图,是的一个外角,若,,则的度数是( )
A. B. C. D.
2.[2025山西太原师范学院附中·月考]在下列条件;①;②;③;④;⑤中,能确定为直角三角形的条件有( )
A.5个 B.4个 C.3个 D.2个
3.[2025四川南充·临考冲刺]如图,中,平分,.,.则的度数为( ).
A. B. C. D.
4.[2025四川成都·期末]如图,直线a∥b,点C,D分别在直线b,a上,AC⊥BC,CD平分∠ACB,若∠1=65°,则∠2的度数为( )
A.65° B.70° C.75° D.80°
5.[2024贵州毕节·期末]如图,的角平分线交于点O,若,.则( )
A. B. C. D.
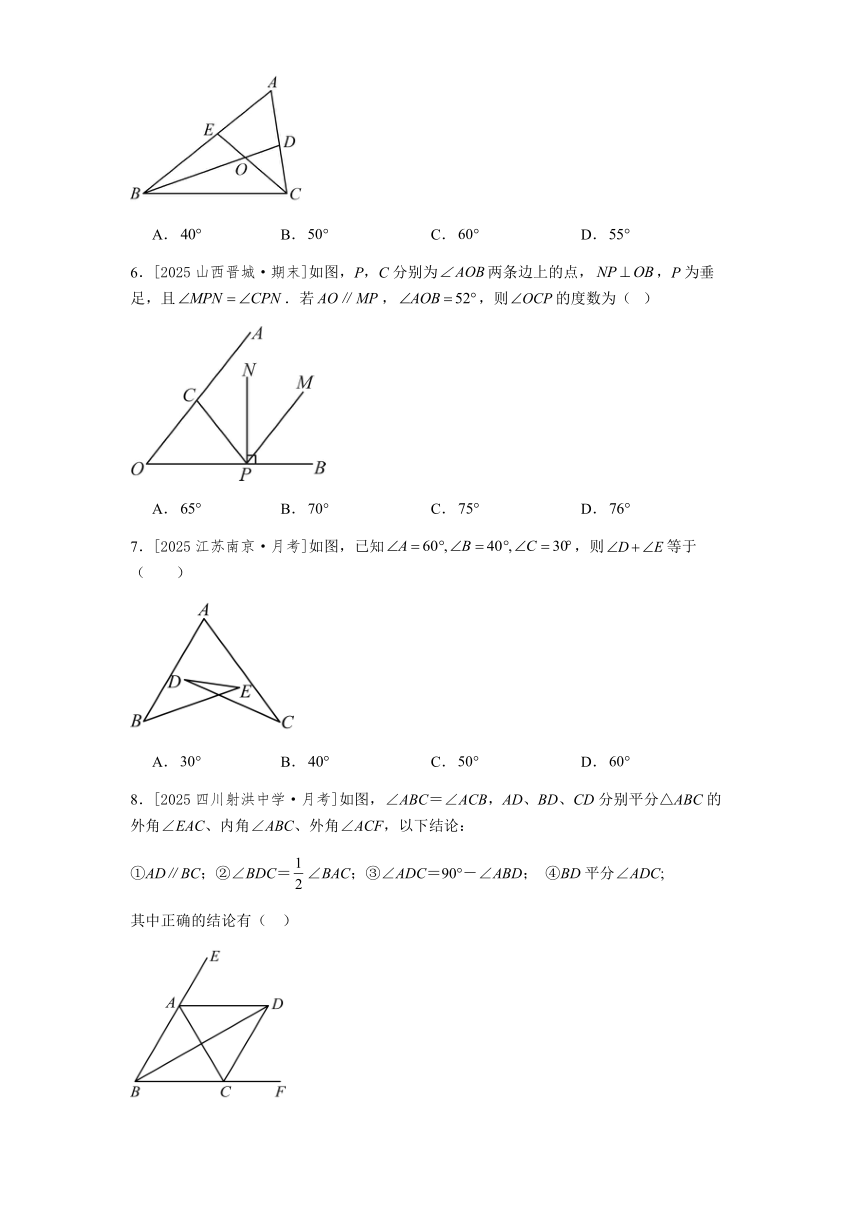
6.[2025山西晋城·期末]如图,P,C分别为两条边上的点,,P为垂足,且.若,,则的度数为( )
A. B. C. D.
7.[2025江苏南京·月考]如图,已知,则等于( )
A. B. C. D.
8.[2025四川射洪中学·月考]如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF,以下结论:
①AD∥BC;②∠BDC=∠BAC;③∠ADC=90°-∠ABD; ④BD平分∠ADC;
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.[2024安徽宣城·期末]在中,,则
10.[2025山西晋城·期末]如图,在中,于点D,平分.若,,则的度数为 .
11.[2025江苏南京·月考]如图,,垂足为E,,,则 .
12.[2025江苏南京·期末]如图,四边形两组对边的延长线分别交于点E,F,,,若与互补,则的度数为 .
13.[2025河南新乡·期末]如图,在中,,D是延长线上一点,是的平分线,分别作,的平分线,交于点E,F,则 °, °.
三、解答题
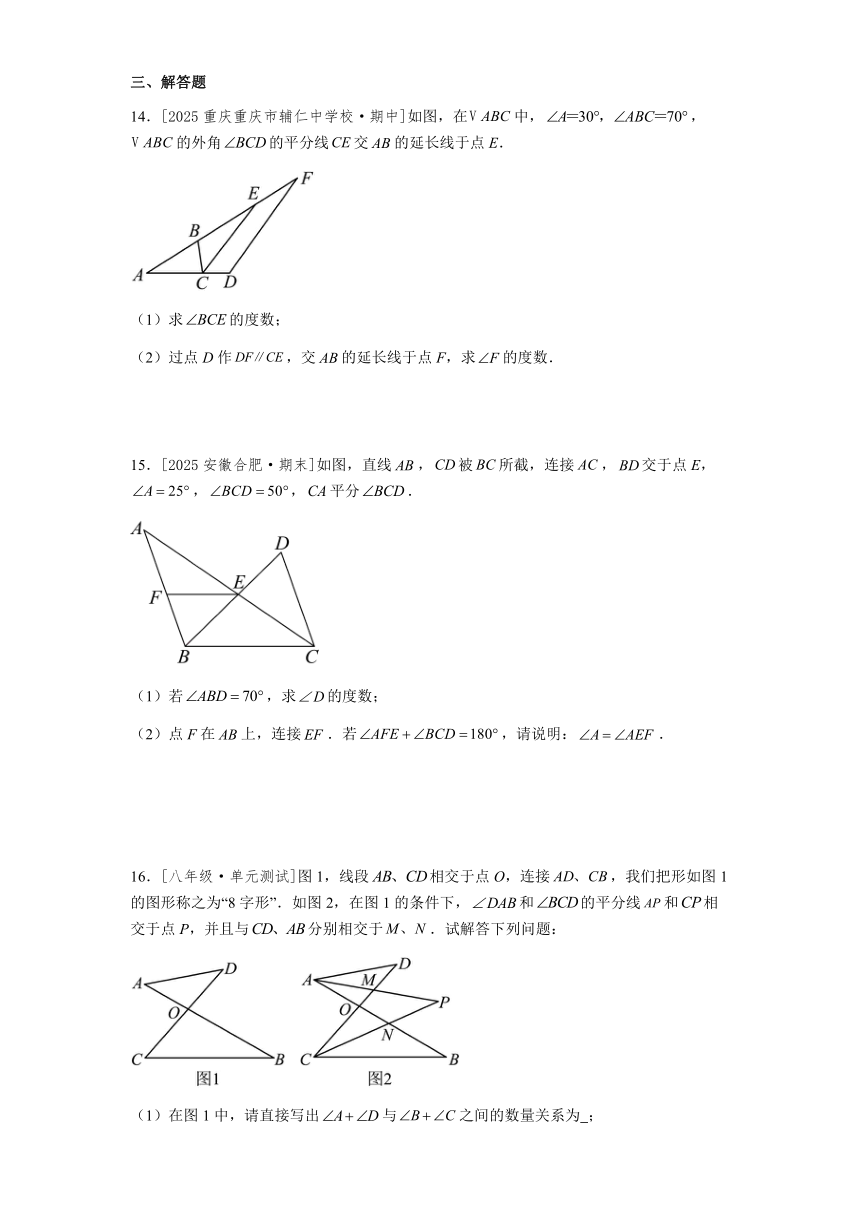
14.[2025重庆重庆市辅仁中学校·期中]如图,在中,,的外角的平分线交的延长线于点E.
(1)求的度数;
(2)过点D作,交的延长线于点F,求的度数.
15.[2025安徽合肥·期末]如图,直线,被所截,连接,交于点E,,,平分.
(1)若,求的度数;
(2)点F在上,连接.若,请说明:.
16.[八年级·单元测试]图1,线段相交于点O,连接,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,和的平分线和相交于点P,并且与分别相交于.试解答下列问题:
(1)在图1中,请直接写出与之间的数量关系为 ;
(2)仔细观察,在图2中“8字形”的个数: 个;
(3)图2中,和为任意角时,其他条件不变,试问与之间存在着怎样的数量关系?说明理由
(4)应用:如图2,当时,直接说出的度数.
17.[2025山西晋城·期末]综合与探究
提出问题:
小冉在学习中遇到这样一个问题:如图1,在中,的平分线与外角的平分线交于点.试猜想与之间的数量关系.
解决问题:
(1)小冉阅读后没有任何思路,同桌小卓提醒小冉,可以尝试先代入的特殊角度,然后根据结果猜想与之间的数量关系.
①若,则________;若,则________;
②通过上面的计算,请猜测与之间的数量关系,并说明理由;
应用拓展:
(2)如图2,将改成四边形,的平分线及一个外角的平分线相交于点F.若,求的度数;
深入探究:
(3)如图3,在中,的平分线与外角的平分线交于点.若E是延长线上一动点,连接,与的平分线交于点Q,在点E移动的过程中,请直接写出与之间的数量关系.
参考答案
1.【答案】C
【分析】
根据三角形的外角的性质即可得到结论.
【详解】
解:∵,的一个外角,
∴.
故选:C.
【点睛】
本题考查三角形外角的性质,三角形的一个外角等于与它不相邻两内角的和.熟练掌握三角形外角的性质是解题的关键.
2.【答案】C
【分析】利用三角形的内角和定理求出角的度数,即可分别进行判断.
【详解】解:①由得到,即,是直角三角形;
②由题可得,是直角三角形;
③由得到2,解得,,不是直角三角形;
④由得到,解得,,,是直角三角形;
⑤由得到,解得,不是直角三角形;
故选C.
3.【答案】D
【分析】先由平分,得,根据,则,再把数值代入,进行计算,即可作答.
【详解】解:∵平分,
∴,
∵,
∴,
在中,,
∴,
即,
解得,
故选D
4.【答案】B
【分析】根据角平分线定义求∠BCD=∠ACB=45°,根据三角形内角和定理得∠2=∠3=180°﹣∠1﹣∠BCD.
【详解】如图,
∵AC⊥BC,
∴∠ACB=90°,
∵CD平分∠ACB,
∴∠BCD=∠ACB=45°,
∵∠1=65°,
∴∠2=∠3=180°﹣∠1﹣∠BCD=70°,
故选B.
5.【答案】C
【分析】根据三角形内角和定理求出,再根据角平分的定义求出,则由三角形外角的性质可得.
【详解】解:∵,,
∴,
∵的角平分线交于点O,
∴,
∴,
故选C.
6.【答案】D
【分析】根据平行线得到,结合题意得出,再根据三角形的内角和定理计算即可.
【详解】解:∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
故选D.
7.【答案】C
【分析】连接.设与交于点,由三角形内角定理求出.再由三角形内角和定理和对顶角相等即可求出.
【详解】如图,连接.设与交于点,
,.
,,
,
故选C.
8.【答案】C
【分析】根据角平分线定义得出∠ABC=2∠ABD=2∠DBC,∠EAC=2∠EAD,∠ACF=2∠DCF,根据三角形的内角和定理得出∠BAC+∠ABC+∠ACB=180°,根据三角形外角性质得出∠ACF=∠ABC+∠BAC,∠EAC=∠ABC+∠ACB,根据已知结论逐步推理,即可判断各项.
【详解】解:∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,
∴①正确;
∵∠ACF=2∠DCF,∠ACF=∠BAC+∠ABC,∠ABC=2∠DBC,∠DCF=∠DBC+∠BDC,
∴∠BAC=2∠BDC,
∠BDC=∠BAC,
∴②正确;
在△ADC中,∠ADC+∠CAD+∠ACD=180°,
∵CD平分△ABC的外角∠ACF,
∴∠ACD=∠DCF,
∵AD∥BC,
∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB
∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,
∴∠ADC+∠ABD=90°
∴∠ADC=90°-∠ABD,
故③正确;
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵∠ADB=∠DBC,∠ADC=90°-∠ABC,
∴∠ADB不等于∠CDB,
∴④不正确;
即正确的有3个,
故选C.
9.【答案】60
【分析】先求出,再根据三角形的内角和定理即可得.
【详解】解:∵,
∴,
∵在中,,
∴.
10.【答案】12
【分析】先求解,,,再进一步求解即可.
【详解】解:在中,,,
∴,
∵,
∴.
在中,,
∵平分,
∴,
∴.
11.【答案】22
【分析】首先根据三角形内角和定理求出,然后根据直角三角形两锐角互余求解即可.
【详解】解:∵,,
∴
∵
∴
∴.
12.【答案】/40度
【分析】连接,可得,再根据三角形外角性质得,则,然后根据三角形内角和定理有,即,再解方程即可.
【详解】解:连接,如图,
∵,,
∴,
∵,
∴,
∵,
∴,
∴.
13.【答案】;
【分析】先利用直角三角形两个锐角互余,得出,再根据角平分线的意义,得出,,结合平角的意义,可求得,再利用角平分线的意义和三角形外角的性质,可求得,从而可利用邻补角的意义求得,再利用直角三角形两个锐角互余,求得.
【详解】解:∵在中,,
∴,
∵,的平分线,
∴,,
∴
,
∵是的平分线,
∴,
,
∵,
∴,解得:,
又,
,
,解得:.
14.【答案】(1)
(2)
【分析】(1)根据三角形外角的性质求出的度数,然后根据角平分线定义求解即可;
(2)根据三角形外角的性质求出的度数,然后根据平行线的性质求解即可.
【详解】(1)解:∵,,
∴,
又平分,
∴;
(2)解:∵,,
∴,
又,
∴.
15.【答案】(1)
(2)见详解
【分析】(1)先利用角平分线的意义求出,再利用三角形内角和求出,进而求出,然后利用三角形内角和求出;
(2)先求出,再利用三角形内角和求出即可.
【详解】(1)解:∵平分,,
∴,
,
,
,
,
,
∴;
(2),,
,
,
,
.
16.【答案】(1)
(2)6
(3),理由见详解;
(4)
【分析】(1)由三角形内角和定理可得,进而可求解;
(2)根据“8字形”的定义即可求解;
(3)由,,和平分和,可得,即可求解;
(4)由(3)中关系式即可求解;
【详解】(1)解:由三角形内角和定理可知,
∵,
∴,
故答案为:;
(2)与与与与与与,共六个;
故答案为:6;
(3)∵,
∴,
∵,
∴,
∵和平分和,
∴、,
∴,
∴.
(4)∵,
由(3)知,
∴.
17.【答案】(1)①30,45;②,见详解;(2);(3)
【分析】(1)①根据角平分线的定义得到,再由三角形外角的性质得到,,由此即可解答;②由①即可解答;
(2)根据角平分线的定义,根据三角形外角的性质得到,利用四边形内角和定理得到,则,由此即可求出;
(3)同理可得,,利用三角形内角和定理得到,再由三角形外角的性质得到,即可得到,由此即可得到结论.
【详解】解:(1)①∵平分平分,
∴,
∵,
∴,
∴,
∴;
若,则;
若,则.
②由①得.
(2)的平分线及一个外角的平分线相交于点,
,.
,
.
,
.
,
.
.
;
(3),理由如下:
同(1)可得,
∵平分平分,
∴,
∵,
∴,
∵,
∴,
∵,
∴.
第 page number 页,共 number of pages 页
学校:___________姓名:___________班级:___________学号:___________
一、单选题
1.如图,是的一个外角,若,,则的度数是( )
A. B. C. D.
2.[2025山西太原师范学院附中·月考]在下列条件;①;②;③;④;⑤中,能确定为直角三角形的条件有( )
A.5个 B.4个 C.3个 D.2个
3.[2025四川南充·临考冲刺]如图,中,平分,.,.则的度数为( ).
A. B. C. D.
4.[2025四川成都·期末]如图,直线a∥b,点C,D分别在直线b,a上,AC⊥BC,CD平分∠ACB,若∠1=65°,则∠2的度数为( )
A.65° B.70° C.75° D.80°
5.[2024贵州毕节·期末]如图,的角平分线交于点O,若,.则( )
A. B. C. D.
6.[2025山西晋城·期末]如图,P,C分别为两条边上的点,,P为垂足,且.若,,则的度数为( )
A. B. C. D.
7.[2025江苏南京·月考]如图,已知,则等于( )
A. B. C. D.
8.[2025四川射洪中学·月考]如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF,以下结论:
①AD∥BC;②∠BDC=∠BAC;③∠ADC=90°-∠ABD; ④BD平分∠ADC;
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.[2024安徽宣城·期末]在中,,则
10.[2025山西晋城·期末]如图,在中,于点D,平分.若,,则的度数为 .
11.[2025江苏南京·月考]如图,,垂足为E,,,则 .
12.[2025江苏南京·期末]如图,四边形两组对边的延长线分别交于点E,F,,,若与互补,则的度数为 .
13.[2025河南新乡·期末]如图,在中,,D是延长线上一点,是的平分线,分别作,的平分线,交于点E,F,则 °, °.
三、解答题
14.[2025重庆重庆市辅仁中学校·期中]如图,在中,,的外角的平分线交的延长线于点E.
(1)求的度数;
(2)过点D作,交的延长线于点F,求的度数.
15.[2025安徽合肥·期末]如图,直线,被所截,连接,交于点E,,,平分.
(1)若,求的度数;
(2)点F在上,连接.若,请说明:.
16.[八年级·单元测试]图1,线段相交于点O,连接,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,和的平分线和相交于点P,并且与分别相交于.试解答下列问题:
(1)在图1中,请直接写出与之间的数量关系为 ;
(2)仔细观察,在图2中“8字形”的个数: 个;
(3)图2中,和为任意角时,其他条件不变,试问与之间存在着怎样的数量关系?说明理由
(4)应用:如图2,当时,直接说出的度数.
17.[2025山西晋城·期末]综合与探究
提出问题:
小冉在学习中遇到这样一个问题:如图1,在中,的平分线与外角的平分线交于点.试猜想与之间的数量关系.
解决问题:
(1)小冉阅读后没有任何思路,同桌小卓提醒小冉,可以尝试先代入的特殊角度,然后根据结果猜想与之间的数量关系.
①若,则________;若,则________;
②通过上面的计算,请猜测与之间的数量关系,并说明理由;
应用拓展:
(2)如图2,将改成四边形,的平分线及一个外角的平分线相交于点F.若,求的度数;
深入探究:
(3)如图3,在中,的平分线与外角的平分线交于点.若E是延长线上一动点,连接,与的平分线交于点Q,在点E移动的过程中,请直接写出与之间的数量关系.
参考答案
1.【答案】C
【分析】
根据三角形的外角的性质即可得到结论.
【详解】
解:∵,的一个外角,
∴.
故选:C.
【点睛】
本题考查三角形外角的性质,三角形的一个外角等于与它不相邻两内角的和.熟练掌握三角形外角的性质是解题的关键.
2.【答案】C
【分析】利用三角形的内角和定理求出角的度数,即可分别进行判断.
【详解】解:①由得到,即,是直角三角形;
②由题可得,是直角三角形;
③由得到2,解得,,不是直角三角形;
④由得到,解得,,,是直角三角形;
⑤由得到,解得,不是直角三角形;
故选C.
3.【答案】D
【分析】先由平分,得,根据,则,再把数值代入,进行计算,即可作答.
【详解】解:∵平分,
∴,
∵,
∴,
在中,,
∴,
即,
解得,
故选D
4.【答案】B
【分析】根据角平分线定义求∠BCD=∠ACB=45°,根据三角形内角和定理得∠2=∠3=180°﹣∠1﹣∠BCD.
【详解】如图,
∵AC⊥BC,
∴∠ACB=90°,
∵CD平分∠ACB,
∴∠BCD=∠ACB=45°,
∵∠1=65°,
∴∠2=∠3=180°﹣∠1﹣∠BCD=70°,
故选B.
5.【答案】C
【分析】根据三角形内角和定理求出,再根据角平分的定义求出,则由三角形外角的性质可得.
【详解】解:∵,,
∴,
∵的角平分线交于点O,
∴,
∴,
故选C.
6.【答案】D
【分析】根据平行线得到,结合题意得出,再根据三角形的内角和定理计算即可.
【详解】解:∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
故选D.
7.【答案】C
【分析】连接.设与交于点,由三角形内角定理求出.再由三角形内角和定理和对顶角相等即可求出.
【详解】如图,连接.设与交于点,
,.
,,
,
故选C.
8.【答案】C
【分析】根据角平分线定义得出∠ABC=2∠ABD=2∠DBC,∠EAC=2∠EAD,∠ACF=2∠DCF,根据三角形的内角和定理得出∠BAC+∠ABC+∠ACB=180°,根据三角形外角性质得出∠ACF=∠ABC+∠BAC,∠EAC=∠ABC+∠ACB,根据已知结论逐步推理,即可判断各项.
【详解】解:∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,
∴①正确;
∵∠ACF=2∠DCF,∠ACF=∠BAC+∠ABC,∠ABC=2∠DBC,∠DCF=∠DBC+∠BDC,
∴∠BAC=2∠BDC,
∠BDC=∠BAC,
∴②正确;
在△ADC中,∠ADC+∠CAD+∠ACD=180°,
∵CD平分△ABC的外角∠ACF,
∴∠ACD=∠DCF,
∵AD∥BC,
∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB
∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,
∴∠ADC+∠ABD=90°
∴∠ADC=90°-∠ABD,
故③正确;
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵∠ADB=∠DBC,∠ADC=90°-∠ABC,
∴∠ADB不等于∠CDB,
∴④不正确;
即正确的有3个,
故选C.
9.【答案】60
【分析】先求出,再根据三角形的内角和定理即可得.
【详解】解:∵,
∴,
∵在中,,
∴.
10.【答案】12
【分析】先求解,,,再进一步求解即可.
【详解】解:在中,,,
∴,
∵,
∴.
在中,,
∵平分,
∴,
∴.
11.【答案】22
【分析】首先根据三角形内角和定理求出,然后根据直角三角形两锐角互余求解即可.
【详解】解:∵,,
∴
∵
∴
∴.
12.【答案】/40度
【分析】连接,可得,再根据三角形外角性质得,则,然后根据三角形内角和定理有,即,再解方程即可.
【详解】解:连接,如图,
∵,,
∴,
∵,
∴,
∵,
∴,
∴.
13.【答案】;
【分析】先利用直角三角形两个锐角互余,得出,再根据角平分线的意义,得出,,结合平角的意义,可求得,再利用角平分线的意义和三角形外角的性质,可求得,从而可利用邻补角的意义求得,再利用直角三角形两个锐角互余,求得.
【详解】解:∵在中,,
∴,
∵,的平分线,
∴,,
∴
,
∵是的平分线,
∴,
,
∵,
∴,解得:,
又,
,
,解得:.
14.【答案】(1)
(2)
【分析】(1)根据三角形外角的性质求出的度数,然后根据角平分线定义求解即可;
(2)根据三角形外角的性质求出的度数,然后根据平行线的性质求解即可.
【详解】(1)解:∵,,
∴,
又平分,
∴;
(2)解:∵,,
∴,
又,
∴.
15.【答案】(1)
(2)见详解
【分析】(1)先利用角平分线的意义求出,再利用三角形内角和求出,进而求出,然后利用三角形内角和求出;
(2)先求出,再利用三角形内角和求出即可.
【详解】(1)解:∵平分,,
∴,
,
,
,
,
,
∴;
(2),,
,
,
,
.
16.【答案】(1)
(2)6
(3),理由见详解;
(4)
【分析】(1)由三角形内角和定理可得,进而可求解;
(2)根据“8字形”的定义即可求解;
(3)由,,和平分和,可得,即可求解;
(4)由(3)中关系式即可求解;
【详解】(1)解:由三角形内角和定理可知,
∵,
∴,
故答案为:;
(2)与与与与与与,共六个;
故答案为:6;
(3)∵,
∴,
∵,
∴,
∵和平分和,
∴、,
∴,
∴.
(4)∵,
由(3)知,
∴.
17.【答案】(1)①30,45;②,见详解;(2);(3)
【分析】(1)①根据角平分线的定义得到,再由三角形外角的性质得到,,由此即可解答;②由①即可解答;
(2)根据角平分线的定义,根据三角形外角的性质得到,利用四边形内角和定理得到,则,由此即可求出;
(3)同理可得,,利用三角形内角和定理得到,再由三角形外角的性质得到,即可得到,由此即可得到结论.
【详解】解:(1)①∵平分平分,
∴,
∵,
∴,
∴,
∴;
若,则;
若,则.
②由①得.
(2)的平分线及一个外角的平分线相交于点,
,.
,
.
,
.
,
.
.
;
(3),理由如下:
同(1)可得,
∵平分平分,
∴,
∵,
∴,
∵,
∴,
∵,
∴.
第 page number 页,共 number of pages 页
同课章节目录
