1.2 矩形的性质与判定 同步练习(含答案)
文档属性
| 名称 | 1.2 矩形的性质与判定 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 458.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-09 13:18:10 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2矩形的性质与判定
一、单选题
1.(2024八上·常州期中)笔直的公路,,如图所示,,互相垂直,的中点D与点C被建筑物隔开,若测得的长为,的长为,则C,D之间的距离为( )
A. B. C. D.
2.(2022八下·武江期末)如图,在中,,点F为AC中点,是的中位线,若,则BF=( )
A.6 B.4 C.3 D.5
3.(2024九下·调兵山模拟)如图,用平移法说明平行四边形的面积公式时, 若平移到,,,则的平移距离为( )
A.1 B.3 C.4 D.5
4.(2024·丹阳模拟)如图,中,,是的中位线,点在上,且.若,,则长为( )
A.1 B.2 C.3 D.4
5.(2023七下·桦南期末)如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
A.∠ABC=90° B.AC=BD C.OA=OB D.OA=AD
6.(2023八下·汝阳期末)下列命题,为真命题的是 ( )
A.三个角是直角的四边形是矩形
B.对角线相等的四边形是矩形
C.三条边相等的四边形是菱形
D.对角线互相垂直的四边形是菱形
7.(2024八下·楚雄期中)如图,已知△ABC中,AB=6,BC=8,AC=10,那么AC边上的中线BD的长为( )
A.3 B.4 C.5 D.6
8.(2024八下·经开期中) 如图,在长方形中,点是上一点,连接,沿直线把折叠,使点恰好落在边上的点处.若,则折痕的长度为( )
A. B.10 C. D.15
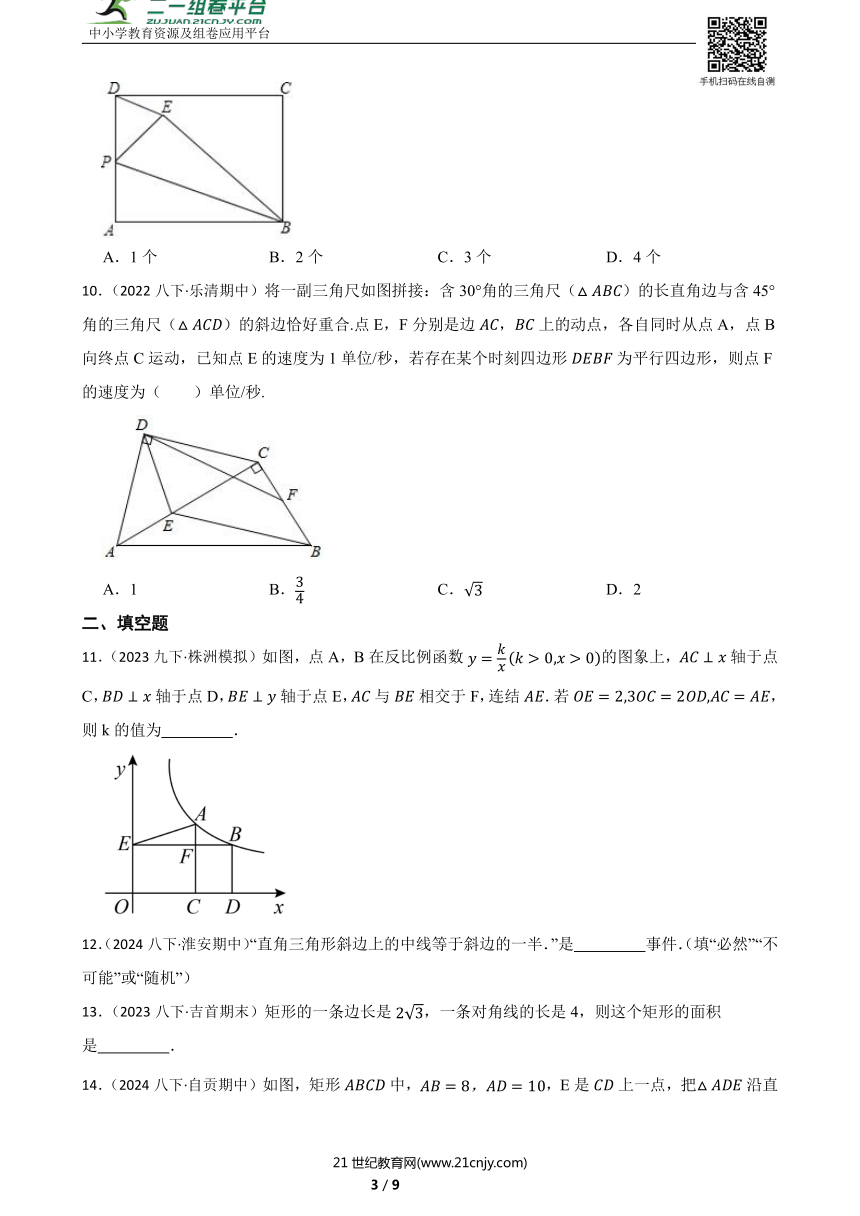
9.(2017·沭阳模拟)如图,矩形ABCD中,AB=10,BC=8,P为AD的中点,将△ABP沿BP翻折至△EBP(点A落到点E处),连接DE,则图中与∠APB相等的角的个数为( )
A.1个 B.2个 C.3个 D.4个
10.(2022八下·乐清期中)将一副三角尺如图拼接:含30°角的三角尺()的长直角边与含45°角的三角尺()的斜边恰好重合.点E,F分别是边,上的动点,各自同时从点A,点B向终点C运动,已知点E的速度为1单位/秒,若存在某个时刻四边形为平行四边形,则点F的速度为( )单位/秒.
A.1 B. C. D.2
二、填空题
11.(2023九下·株洲模拟)如图,点A,B在反比例函数的图象上,轴于点C,轴于点D,轴于点E,与相交于F,连结.若,则k的值为 .
12.(2024八下·淮安期中)“直角三角形斜边上的中线等于斜边的一半.”是 事件.(填“必然”“不可能”或“随机”)
13.(2023八下·吉首期末)矩形的一条边长是,一条对角线的长是4,则这个矩形的面积是 .
14.(2024八下·自贡期中)如图,矩形中,,E是上一点,把沿直线翻折,D点恰好落在边上的F点处,则 .
15.(2024九上·金堂期中)如图,在矩形中,,,点E为的中点,将沿折叠,使点B落在矩形内点F处,连接,则的长为 .
16.(2020九上·简阳月考)如图,在矩形 中, , ,点 是线段 上的一点(不与点 , 重合),将△ 沿 折叠,使得点 落在 处,当△ 为等腰三角形时, 的长为 .
三、计算题
17.(2024八上·凉州期中)在直角三角形中,是边上的高,
(1)求的面积;
(2)求的长;
(3)若的边上的中线是,求出的面积.
18.(2024八下·惠州月考)现有一长方形纸片,在剪纸过程中需要折叠.如图,将沿折叠,使点D恰好落在边上的点F处.已知,求的长.
四、解答题
19.(2024八下·陇南期中)如图,在矩形中,点为边上一点,,交于点,若,矩形的周长为16,且,求矩形的面积.
20.(2024八下·安顺期末)已知:如图,矩形的对角线、相交于点,,交的延长线于点.
(1)求证:四边形是平行四边形;
(2)若,求的长.
21.(2022八下·黄山期末)如图,已知矩形ABCD,AB=4,AD=6,点E是BC的中点,将△DCE沿DE折叠得到ΔDC1E,连接BC1、CC1,CC1与DE交于点G.求BC1的长度.
22.(2023八下·栾城期中)如图,在直角坐标系中,一次函数的图象与轴交于点(),与轴交于点,与一次函数的图象交于点.
(1)求的函数表达式;
(2)直线与轴交于点,求的面积;
(3)如图,已知长方形,,,,矩形的边在轴上平移,若矩形与直线或有交点,直接写出的取值范围.
答案解析部分
1.【答案】C
【知识点】勾股定理;直角三角形斜边上的中线
2.【答案】A
【知识点】三角形的中位线定理;直角三角形斜边上的中线
3.【答案】C
【知识点】矩形的判定与性质;平移的性质
4.【答案】A
【知识点】勾股定理;三角形的中位线定理;直角三角形斜边上的中线
5.【答案】D
【知识点】矩形的性质
6.【答案】A
【知识点】菱形的判定;矩形的判定;真命题与假命题
7.【答案】C
【知识点】勾股定理的逆定理;直角三角形斜边上的中线
8.【答案】C
【知识点】勾股定理;矩形的性质;翻折变换(折叠问题)
9.【答案】D
【知识点】矩形的性质;翻折变换(折叠问题)
10.【答案】A
【知识点】平行四边形的性质;直角三角形斜边上的中线
11.【答案】
【知识点】勾股定理;矩形的判定与性质
12.【答案】必然
【知识点】事件的分类;直角三角形斜边上的中线
13.【答案】
【知识点】勾股定理;矩形的性质
14.【答案】3
【知识点】勾股定理;矩形的性质
15.【答案】
【知识点】等腰三角形的判定与性质;勾股定理;矩形的性质;矩形的判定与性质
16.【答案】 或
【知识点】等腰三角形的判定;勾股定理;矩形的性质;翻折变换(折叠问题)
17.【答案】(1)
(2)
(3)
【知识点】三角形的角平分线、中线和高;直角三角形斜边上的中线
18.【答案】3
【知识点】勾股定理;矩形的性质
19.【答案】
【知识点】矩形的性质
20.【答案】(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
又∵BD∥CE,
四边形DCEB是平行四边形;
(2)解:∵四边形ABCD是矩形,
∴AC=BD,
四边形是平行四边形,
,
,
,
.
【知识点】平行四边形的判定与性质;矩形的性质
21.【答案】解:四边形ABCD是矩形,
∴DC=AB=4,BC=AD=6,∠DCB=90°,
∵E是BC中点,
∴BE=EC=BC=3,
∴在RtΔDCE中,
,
而ΔDCE沿DE折叠得ΔDC1E,
∴C1E=EC=BE,
∴∠BC1E=∠EBC1,
∠EC1C=∠ECC1,
∴∠BC1C=90°,
∵DE是折痕,
∴DE⊥C1C且DE平分C1C,
,
∴,
∴ ,
∴在RtΔBCC1中,
【知识点】勾股定理;矩形的性质;翻折变换(折叠问题)
22.【答案】(1)
(2)
(3)当时,矩形与直线有交点,当时,矩形与直线有交点
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系;矩形的性质;平移的性质
21世纪教育网(www.21cnjy.com)
9 / 9
2矩形的性质与判定
一、单选题
1.(2024八上·常州期中)笔直的公路,,如图所示,,互相垂直,的中点D与点C被建筑物隔开,若测得的长为,的长为,则C,D之间的距离为( )
A. B. C. D.
2.(2022八下·武江期末)如图,在中,,点F为AC中点,是的中位线,若,则BF=( )
A.6 B.4 C.3 D.5
3.(2024九下·调兵山模拟)如图,用平移法说明平行四边形的面积公式时, 若平移到,,,则的平移距离为( )
A.1 B.3 C.4 D.5
4.(2024·丹阳模拟)如图,中,,是的中位线,点在上,且.若,,则长为( )
A.1 B.2 C.3 D.4
5.(2023七下·桦南期末)如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
A.∠ABC=90° B.AC=BD C.OA=OB D.OA=AD
6.(2023八下·汝阳期末)下列命题,为真命题的是 ( )
A.三个角是直角的四边形是矩形
B.对角线相等的四边形是矩形
C.三条边相等的四边形是菱形
D.对角线互相垂直的四边形是菱形
7.(2024八下·楚雄期中)如图,已知△ABC中,AB=6,BC=8,AC=10,那么AC边上的中线BD的长为( )
A.3 B.4 C.5 D.6
8.(2024八下·经开期中) 如图,在长方形中,点是上一点,连接,沿直线把折叠,使点恰好落在边上的点处.若,则折痕的长度为( )
A. B.10 C. D.15
9.(2017·沭阳模拟)如图,矩形ABCD中,AB=10,BC=8,P为AD的中点,将△ABP沿BP翻折至△EBP(点A落到点E处),连接DE,则图中与∠APB相等的角的个数为( )
A.1个 B.2个 C.3个 D.4个
10.(2022八下·乐清期中)将一副三角尺如图拼接:含30°角的三角尺()的长直角边与含45°角的三角尺()的斜边恰好重合.点E,F分别是边,上的动点,各自同时从点A,点B向终点C运动,已知点E的速度为1单位/秒,若存在某个时刻四边形为平行四边形,则点F的速度为( )单位/秒.
A.1 B. C. D.2
二、填空题
11.(2023九下·株洲模拟)如图,点A,B在反比例函数的图象上,轴于点C,轴于点D,轴于点E,与相交于F,连结.若,则k的值为 .
12.(2024八下·淮安期中)“直角三角形斜边上的中线等于斜边的一半.”是 事件.(填“必然”“不可能”或“随机”)
13.(2023八下·吉首期末)矩形的一条边长是,一条对角线的长是4,则这个矩形的面积是 .
14.(2024八下·自贡期中)如图,矩形中,,E是上一点,把沿直线翻折,D点恰好落在边上的F点处,则 .
15.(2024九上·金堂期中)如图,在矩形中,,,点E为的中点,将沿折叠,使点B落在矩形内点F处,连接,则的长为 .
16.(2020九上·简阳月考)如图,在矩形 中, , ,点 是线段 上的一点(不与点 , 重合),将△ 沿 折叠,使得点 落在 处,当△ 为等腰三角形时, 的长为 .
三、计算题
17.(2024八上·凉州期中)在直角三角形中,是边上的高,
(1)求的面积;
(2)求的长;
(3)若的边上的中线是,求出的面积.
18.(2024八下·惠州月考)现有一长方形纸片,在剪纸过程中需要折叠.如图,将沿折叠,使点D恰好落在边上的点F处.已知,求的长.
四、解答题
19.(2024八下·陇南期中)如图,在矩形中,点为边上一点,,交于点,若,矩形的周长为16,且,求矩形的面积.
20.(2024八下·安顺期末)已知:如图,矩形的对角线、相交于点,,交的延长线于点.
(1)求证:四边形是平行四边形;
(2)若,求的长.
21.(2022八下·黄山期末)如图,已知矩形ABCD,AB=4,AD=6,点E是BC的中点,将△DCE沿DE折叠得到ΔDC1E,连接BC1、CC1,CC1与DE交于点G.求BC1的长度.
22.(2023八下·栾城期中)如图,在直角坐标系中,一次函数的图象与轴交于点(),与轴交于点,与一次函数的图象交于点.
(1)求的函数表达式;
(2)直线与轴交于点,求的面积;
(3)如图,已知长方形,,,,矩形的边在轴上平移,若矩形与直线或有交点,直接写出的取值范围.
答案解析部分
1.【答案】C
【知识点】勾股定理;直角三角形斜边上的中线
2.【答案】A
【知识点】三角形的中位线定理;直角三角形斜边上的中线
3.【答案】C
【知识点】矩形的判定与性质;平移的性质
4.【答案】A
【知识点】勾股定理;三角形的中位线定理;直角三角形斜边上的中线
5.【答案】D
【知识点】矩形的性质
6.【答案】A
【知识点】菱形的判定;矩形的判定;真命题与假命题
7.【答案】C
【知识点】勾股定理的逆定理;直角三角形斜边上的中线
8.【答案】C
【知识点】勾股定理;矩形的性质;翻折变换(折叠问题)
9.【答案】D
【知识点】矩形的性质;翻折变换(折叠问题)
10.【答案】A
【知识点】平行四边形的性质;直角三角形斜边上的中线
11.【答案】
【知识点】勾股定理;矩形的判定与性质
12.【答案】必然
【知识点】事件的分类;直角三角形斜边上的中线
13.【答案】
【知识点】勾股定理;矩形的性质
14.【答案】3
【知识点】勾股定理;矩形的性质
15.【答案】
【知识点】等腰三角形的判定与性质;勾股定理;矩形的性质;矩形的判定与性质
16.【答案】 或
【知识点】等腰三角形的判定;勾股定理;矩形的性质;翻折变换(折叠问题)
17.【答案】(1)
(2)
(3)
【知识点】三角形的角平分线、中线和高;直角三角形斜边上的中线
18.【答案】3
【知识点】勾股定理;矩形的性质
19.【答案】
【知识点】矩形的性质
20.【答案】(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
又∵BD∥CE,
四边形DCEB是平行四边形;
(2)解:∵四边形ABCD是矩形,
∴AC=BD,
四边形是平行四边形,
,
,
,
.
【知识点】平行四边形的判定与性质;矩形的性质
21.【答案】解:四边形ABCD是矩形,
∴DC=AB=4,BC=AD=6,∠DCB=90°,
∵E是BC中点,
∴BE=EC=BC=3,
∴在RtΔDCE中,
,
而ΔDCE沿DE折叠得ΔDC1E,
∴C1E=EC=BE,
∴∠BC1E=∠EBC1,
∠EC1C=∠ECC1,
∴∠BC1C=90°,
∵DE是折痕,
∴DE⊥C1C且DE平分C1C,
,
∴,
∴ ,
∴在RtΔBCC1中,
【知识点】勾股定理;矩形的性质;翻折变换(折叠问题)
22.【答案】(1)
(2)
(3)当时,矩形与直线有交点,当时,矩形与直线有交点
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系;矩形的性质;平移的性质
21世纪教育网(www.21cnjy.com)
9 / 9
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
