五年级暑假专项训练:填空题(含解析)-2024-2025学年下学期小学数学苏教版
文档属性
| 名称 | 五年级暑假专项训练:填空题(含解析)-2024-2025学年下学期小学数学苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 258.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 21:54:39 | ||
图片预览



文档简介
五年级暑假专项训练:填空题(含解析)-2024-2025学年下学期小学数学苏教版
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.图中黑棋子占棋子总数的。如果增加1枚黑棋子,那么黑棋子占棋子总数的;如果增加1枚白棋子,黑棋子占棋子总数的。
2.在14、6、15、24中, 是 的因数, 是 的倍数.
3.图中阴影部分表示( )吨。
4.甲、乙两人骑摩托车同时从一个地点向相反方向开出,3小时后两人相距240千米。已知乙的速度是35千米/时,甲的速度是( )千米/时。
5.把质量为3千克的西瓜平均切成8块,每块西瓜重( )千克,每块西瓜的质量占西瓜总质量的( ).
6.用5千克黄豆可制成豆腐22千克,每千克黄豆可制豆腐千克,每千克豆腐需要黄豆千克。
7.甲数的最大因数是36,乙数的最小倍数是24,甲乙两数的最大公因数是( ),最小公倍数是( )。
8.填空:在同一圆内,半径与直径都有 条,半径的长度是直径的 ,直径与半径的长度比是 .
9.一个四位数千位是最小的奇数,百位是最小的合数,十位是最小的质数,其它数位上是0,这个数写作 ,它既是 又是 的倍数.
10.的分子加上4,为使分数的大小不变,分母应加上 。
11.在同一个圆里,周长是直径的 倍.
12.将一个圆平均分成32等份后拼成一个近似的长方形。如果测得这个长方形的长为6.28分米,那么原来的圆的面积是( )平方分米,长方形的周长是( )分米。
13.。
14.用长3厘米、宽2厘米的长方形能够拼成图( )正方形(填序号)。我是这样想的:( )。
15.从0、3、5、8这四个数字中选两个数字组成一个两位数:( )既是5的倍数,又是3的倍数;最大的偶数是( );最小的奇数是( ),写出一个质数( )。
16.10是10的 数,也是10的 数.
17.用边长是( )分米、( )分米或( )分米的正方形瓷砖,都能正好铺满一个长16分米、宽12分米的长方形墙面,而且不需要切割。
18.五年级学生分组举行“我的中国梦”科技比赛。如果五(1)班学生每组5人或每组8人都少3人,五(1)班最少有( )名学生。
19.如果a÷b=6(ab为非0自然数),那么a和b的最大公因数是( ),最小公倍数是( )。
20.a是大于0的自然数。当a=( )时,是最大的真分数;当a=( )时,是最小的假分数。
21.在括号里填最简分数。
80厘米=( )米 25秒=( )分 60千克=( )吨
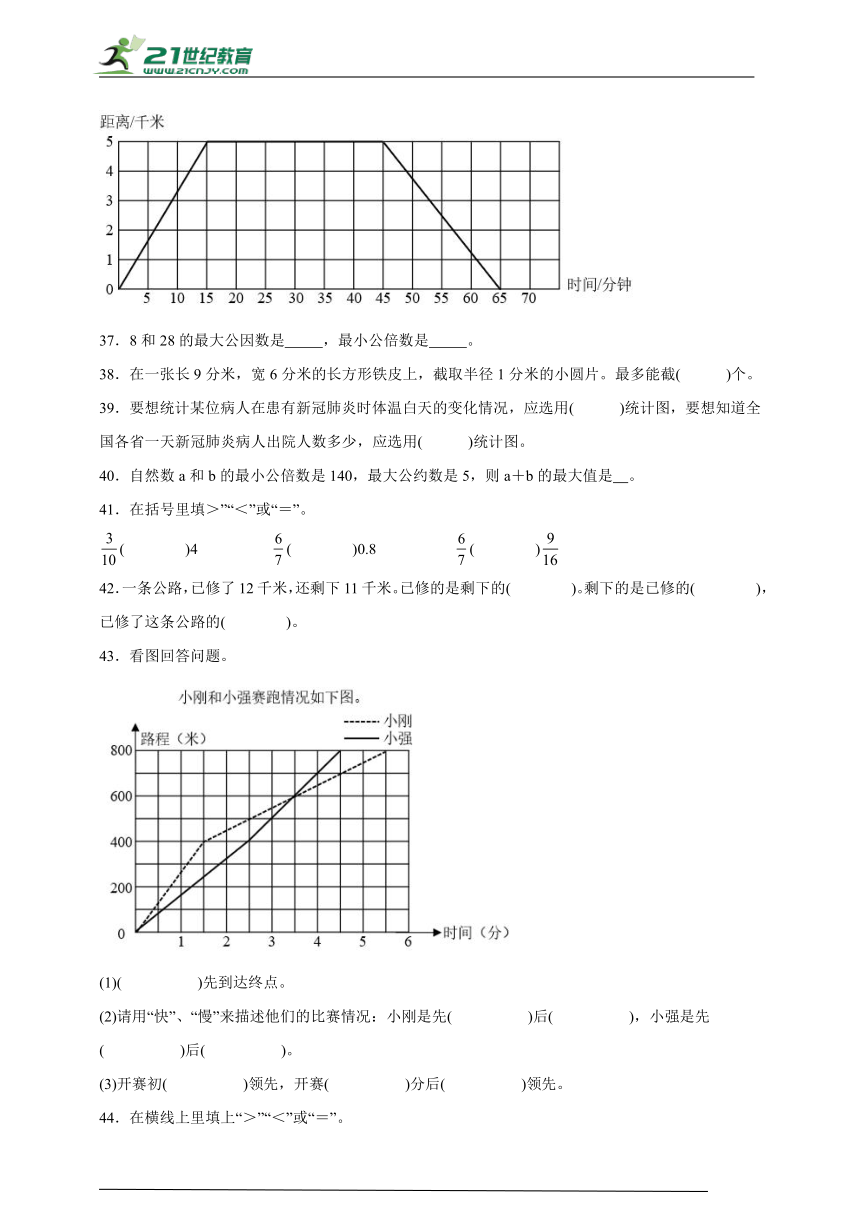
22.用圆规画圆, 决定圆的位置, 决定圆的大小。画周长是15.7cm的圆,圆规两脚间的距离应是 cm。
23.27和9的最大公因数是( );34和51的最小公倍数是( )。
24.某班的学生接近50人。在一次数学竞赛中,该班学生人数的获得一等奖,获得二等奖,获得三等奖,这个班的学生可能是 人。
25.已知2 3=2+3+4=9,5 4=5+6+7+8=26,若x 3=15,则x=( )
26.在既是2,3的倍数,又是5的倍数的数中,最大的两位数是( ),最大的三位数是( )。
27.把三根长分别是60厘米、36厘米、24厘米的绳子剪成同样长的小段,没有剩余,每段最长是( )厘米,此时共有( )小段。
28.3333×7777+5555的结果是( )(填“奇数”或“偶数”)。
29.下列算式中,□,○,△,☆各代表什么数?
(1)□+5=13-6;(2)28-○=15+7;(3)3×△=54;(4)56÷☆=7
□= ,○= ,△= ,☆= 。
30.49秒=分 7厘米=分米 13千克=吨
31.一个长方形的长是8厘米,宽是4厘米.在这个长方形里画直径4厘米的圆,最多能画( )个,剩下部分的面积是( )平方厘米.
32.三个连续偶数,如果中间的数是m,那么这三个数的和是( );如果这三个数的和是84,那么最大数是( )。
33.有12枝铅笔,平均分给2个同学。每枝铅笔是铅笔总数的,每人分得的铅笔是铅笔总数的 。
34.在0.75、、、0.7四个数中,最大的是( ),最小的是( ),相等的是( )和( )。
35.如图,将一个半径2厘米的圆形纸片平均分成若干份,剪开后拼成一个近似的长方形,拼成的近似长方形的周长是( )厘米。
36.小华骑车从家出发,去离家5千米远的书店买书,然后再骑车回家。如图表示这段时间小华离家距离的变化情况。
(1)小华在书店待了( )分钟,回家路上用了( )分钟。
(2)小华从家去书店平均每分钟行( )千米。
37.8和28的最大公因数是 ,最小公倍数是 。
38.在一张长9分米,宽6分米的长方形铁皮上,截取半径1分米的小圆片。最多能截( )个。
39.要想统计某位病人在患有新冠肺炎时体温白天的变化情况,应选用( )统计图,要想知道全国各省一天新冠肺炎病人出院人数多少,应选用( )统计图。
40.自然数a和b的最小公倍数是140,最大公约数是5,则a+b的最大值是 。
41.在括号里填>”“<”或“=”。
( )4 ( )0.8 ( )
42.一条公路,已修了12千米,还剩下11千米。已修的是剩下的( )。剩下的是已修的( ),已修了这条公路的( )。
43.看图回答问题。
(1)( )先到达终点。
(2)请用“快”、“慢”来描述他们的比赛情况:小刚是先( )后( ),小强是先( )后( )。
(3)开赛初( )领先,开赛( )分后( )领先。
44.在横线上里填上“>”“<”或“=”。
0.83 (a为非0自然数)
45.填表。
半径(r) 直径(d) 周长(C) 面积(S)
( ) 14dm ( ) ( )
( ) ( ) 21.98cm ( )
46. 叫做圆周率,用字母 表示,它是一个 小数,保留两位小数约为 .
47.鞋的尺码是指鞋底的长度,通常用“码”或“厘米”作单位。码和厘米可以用下面的公式换算:厘米数×2-10=码数。张华穿36码的鞋,他的鞋长是( )厘米。
48.a、b为不是0的自然数。若a÷b=3,则a,b的最大公因数是( ),最小公倍数是( )。若a=b+1,则a,b的最大公因数是( ),最小公倍数是( )。
49.91的所有因数有: .
《五年级暑假专项训练:填空题(含解析)-2024-2025学年下学期小学数学苏教版》参考答案
1.;;
【分析】黑棋子有5枚,棋子总数有15枚,求黑棋子占棋子总数的几分之几用除法;增加1枚黑棋子,黑棋子有(5+1)枚,棋子总数有(15+1)枚,求黑棋子占棋子总数的几分之几用除法;增加1枚白棋子,黑棋子有5枚,棋子总数有(15+1)枚,求黑棋子占棋子总数的几分之几用除法;据此解答。
【详解】5÷15=
(5+1)÷(15+1)
=6÷16
=
5÷(15+1)
=5÷16
=
【点睛】本题主要考查求一个数是另一个数的几分之几,用除法,解题时注意总数的变化。
2.6,24,24,6
【详解】试题分析:一个整数除以一个不为0的整数,得到的商是整数,而没有余数,就说一个数是另一个数的倍数,另一个数就是一个数的因数,据此解答即可.
解:因为24÷6=4,说明6是24的因数,24是6的倍数.
故答案为6,24,24,6.
点评:此题主要考查约数与倍数的意义及其运用.
3.
【分析】观察图形,把3吨的整体平均分成了4份,阴影部分占其中一份,要计算这一份是多少应该用3除以4,根据分数与除法的关系可知,计算结果为。
【详解】3÷4=(吨)
图中阴影部分表示吨。
4.45
【分析】根据题意,甲、乙两车同时从一个地点向相反的方向开出3小时后相距240千米,也就是甲乙两人行驶的总路程等于240千米;甲的速度加乙的速度是速度和,它们之间的数量关系是速度和×时间=总路程。可以假设甲的速度是x千米/时,根据数量关系列式解答即可。
【详解】解:设甲的速度是x千米/时。
(x+35)×3=240
(x+35)×3÷3=240÷3
x+35=80
x+35-35=80-35
x=45
甲的速度是45千米/时。
5.
【详解】略
6.;
【分析】用豆腐的质量除以黄豆的质量,即可求出每千克黄豆克制豆腐多少千克;用黄豆的质量除以豆腐的质量,即可求出每千克豆腐需要黄豆多少千克,即可解答。
【详解】22÷5=(千克)
5÷22=(千克)
【点睛】本题考查分数的意义,关键是找清楚谁是单一量,然后把另一个量进行平均分。
7. 12 72
【分析】一个数的最大因数是它本身;一个数的最小倍数是它本身。据此可得:甲数是36,乙数是24。
用质因数分解法可以求两个数的最大公因数和最小公倍数。全部共有的质因数(公有质因数)相乘的积就是这两个数的最大公因数;全部公有的质因数和各自独立的质因数,它们连乘的积就是这两个数的最小公倍数。据此解答。
【详解】通过分析可得:甲数是36,乙数是24。
36=2×2×3×3
24=2×2×2×3
则甲乙两数的最大公因数是2×2×3=12,最小公倍数是2×2×3×2×3=72。
8.无数,一半,2:1
【详解】试题分析:在同一圆内,直径的长度是半径的两倍,由此进行做题.
解:由题意知,在同一圆内,半径与直径都有无数条,半径的长度是直径的一半,直径与半径的长度比是2:1.
故答案为无数,一半,2:1.
点评:此题考查了在同一圆内圆的半径和直径的关系.
9.1420,2的倍数,5
【详解】试题分析:(1)最小的奇数是1,最小的合数是4,最小的质数是2;可知这个四位数的千位上是1,百位上是4,十位上是2,个位上是0,写出此数即可;
(2)能被2整除的数的特征:个位上是0、2、4、6、8;能被5整除的数的特征:个位上是0或5,据此进行判断.
解;(1)最小的奇数是1,最小的合数是4,最小的质数是2,所以这个四位数写作:1420;
(2)1420的个位上是0,所以1420既是2的倍数又是5的倍数.
故答案为1420,2的倍数,5.
点评:解答本题要明确奇数、质数、合数的概念和能被2、5整除的数的特征.
10.18
【详解】原分数分子是2,现在分数的分子是2+4=6,扩大3倍,即
9×3=27
27-9=18
分母应加上18。
【点睛】此题主要利用分数的基本性质解答问题,先观察分子或分母之间的变化,发现规律,再进一步通过计算解答问题。
11.π
【分析】根据圆周率的含义:圆周率等于圆的周长和它直径的比值,用字母“π”表示;由此解答即可.
【详解】根据圆周率的含义可知:圆周长总是它直径长度的π倍,π取近似值为3.14;
故答案为π.
12. 12.56 16.56
【分析】将一个圆拼成一个近似的长方形,长方形的长=圆周长的一半(πr),长方形的宽=圆的半径(r)。由长方形的长为6.28分米,可求得圆的半径(宽),根据圆的面积公式代入数据即可求得圆的面积,根据长方形的周长=(长+宽)×2代入数据即可求得长方形的周长。
【详解】半径:6.28÷3.14=2(分米)
圆的面积:3.14×22=12.56(平方分米)
长方形的周长:(6.28+2)×2
=8.28×2
=16.56(分米)
故答案为:12.56;16.56
【点睛】本题主要考查圆的面积公式,解题的关键是理解“将一个圆拼成一个近似的长方形,长方形的长=圆周长的一半,长方形的宽=圆的半径”。
13.1;10;3
【分析】根据小数化分数的方法先将0.5化成分数,再根据分数的基本性质即分数与除法的关系填空即可。
【详解】;
;
即
【点睛】熟练掌握小数化分数的方法、分数的基本性质、分数与除法的关系是解题关键。
14. ② 用长3厘米、宽2厘米的长方形拼成正方形,正方形的边长既是3的倍数也是2的倍数,12既是3的倍数也是2的倍数,所以可以拼成边长是12厘米的正方形
【分析】用长3厘米、宽2厘米的长方形拼成正方形,正方形的边长既是3的倍数也是2的倍数,12既是3的倍数也是2的倍数,所以可以拼成边长是12厘米的正方形,能够拼成图②正方形,据此解答即可。
【详解】用长3厘米、宽2厘米的长方形能够拼成图②正方形。我是这样想的:用长3厘米、宽2厘米的长方形拼成正方形,正方形的边长既是3的倍数也是2的倍数,12既是3的倍数也是2的倍数,所以可以拼成边长是12厘米的正方形。(答案不唯一,合理即可)
【点睛】本题考查最小公倍数,解答本题的关键是掌握最小公倍数的概念。
15. 30 80 35 53
【分析】既是3的倍数又是5的倍数的特征:个位上的数字是0或5,各个数位上的数字的和是3的倍数的数。整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。一个大于1的自然数,除了1和它本身以外不再有其他因数,这样的数叫质数。一个大于1的自然数,除了1和它本身以外还有其他因数,这样的数叫合数。组成的两位数是质数的有53、83。据此解答。
【详解】从0、3、5、8这四个数字中选两个数字组成一个两位数:30既是5的倍数,又是3的倍数;最大的偶数是80;最小的奇数是35,写出一个质数53。
16.因,倍
【详解】试题分析:根据一个数的因数是有限的,其中最大的因数是它本身,一个数的倍数的个数是无限的,其中最小的倍数是它本身,据此解答.
解:10是10的因数,也是10的倍数;
故答案为因,倍.
点评:本题主要考查因数倍数的意义,注意个数的最大的因数是它本身,一个数的最小的倍数是它本身.
17. 1 2 4
【分析】正方形瓷砖刚好铺满长方形的墙面,可得正方形的边长应该是长方形长和宽的公因数,找出16和12的公因数即可。
【详解】16的因数有:1,2,4,8,16;
12的因数有:1,2,3,4,6,12;
所以16和12的公因数有:1,2,4
【点睛】此题考查了两个数公因数的求法,关键是要理解正方形瓷砖的边长是长方形长和宽的公因数。
18.37
【分析】由题意可知,五(1)班的人数是5和8的最小公倍数减3,据此解答。
【详解】5和8互质,它们的最小公倍数是5×8=40,40-3=37(人),五(1)班最少有37人。
【点睛】此题主要考查最小公倍数的实际应用,注意少3人,记得最后减3。
19. b a
【分析】两个数为倍数关系,则最大公因数是较小的数,最小公倍数为较大的数;两个数互质,则最大公因数是1。
【详解】因为a÷b=6(a、b为非0自然数),所以a与b的最大公因数为b,最小公倍数为a。
【点睛】熟练掌握求两个数最大公因数与最小公倍数的方法是解题的关键。
20. 7 6
【分析】分子比分母小的分数叫做真分数。分子比分母大或分子和分母相等的分数叫做假分数。
分数大小的比较:分母相同时,分子越大,分数值就越大;分子相同时,分母越大,分数值反而越小。
【详解】是真分数,则a>6;因为>>>……,所以当a=7时,是最大的真分数。
是假分数,则a≥6;因为<<<<……,所以当a=6时,是最小的假分数。
21.
【分析】根据1米=100厘米,1分=60秒,1吨=1000千克,单位小变大除以进率,用小单位数据÷进率,根据分数与除法的关系,即分数的分子相当于被除数,分母相当于除数,表示出结果,约分即可。
【详解】80÷100==(米)
25÷60==(分)
60÷1000==(吨)
22. 圆心 半径 2.5
【分析】根据圆心决定圆的位置;半径决定圆的大小;圆规两脚间的距离是圆的半径,再根据圆的周长公式:周长=2πr,求出圆的半径,即可。
【详解】周长是15.7cm圆的半径:15.7÷3.14÷2
=5÷2
=2.5(厘米)
用圆规画圆,圆心决定圆的位置,半径决定圆的大小。画周长是15.7cm的圆,圆规两脚间的距离应是2.5cm。
【点睛】本题考查圆的特点,应注重基础知识的理解和运用。
23. 9 102
【分析】两个数的最大公因数是两个数的公有质因数的连乘积;两个数的最小公倍数是两个数的公有质因数与每一个数独有质因数的连乘积;如果两个数为倍数关系,较小的数为最大公因数;较大的那个数为最小公倍数;如果两个数为互质数,最大公因数是1,最小公倍数是两个数的乘积,据此解答。
【详解】27是9的倍数,27和9的最大公因数是9;
34=2×17
51=3×17
34和51的最小公倍数是2×3×17=102
27和9的最大公因数是9;34和54的最小公倍数是102。
【点睛】熟练掌握最大公因数和最小公倍数的求法是解答本题的关键。
24.36
【分析】根据题意可知,这个班的人数一定是这几个分数分母的公倍数,先求出这几个分数分母的最小公倍数,然后与条件中的50人对比即可解答。
【详解】12=3×2×2;
4=2×2;
9=3×3;
12、4、9的最小公倍数是3×2×2×3=36;
36接近50,这个班的学生可能是36人。
【点睛】本题主要考查公倍数的应用,理解班级人数是12、4、9的公倍数是解题的关键。
25.4
【分析】观察等式,可知2 3表示从2开始,3个连续自然数的和,5 4表示从5开始,4个连续自然数的和,由此可知x 3表示从x开始,3个连续自然数的和,据此列方程求解即可。
【详解】由x 3=15,得:
x+(x+1)+(x+2)=15
3x+3=15
3x=12
x=4
故答案为:4。
【点睛】本题考查定义新运算,关键是根据已知等式,正确理解新定义的运算规则。
26. 90 990
【分析】个位上是0,2,4,6或8的数,都是2的倍数。个位上是0或5的数,都是5的倍数。一个数各位上的数的和是3的倍数,这个数就是3的倍数。既是2和3的倍数,又是5的倍数,这个数的个位上的数字是0,各个数位上的数字的和是3的倍数。
【详解】在既是2,3的倍数,又是5的倍数的数中,最大的两位数是90,最大的三位数是990。
27. 12 10
【分析】求每段最长几厘米,就是求出这三根绳子长度的最大公因数,由此可以解决问题。用60、36和24分别除以它们的最大公因数的和就是一共能剪成多少段。
【详解】60、36、24的最大公因数是12,所以每段最长是12厘米。
60÷12+36÷12+24÷12
=5+3+2
=8+2
=10(段)
此时共有10小段。
【点睛】此题考查了求几个数的最大公因数在实际问题中的灵活应用,由此可以解决问题。
28.偶数
【分析】把3333×7777+5555化为:1111×(3333×7+5);计算出3333×7+5的结果,如果结果是偶数,那么根据奇数×偶数=偶数;如果结果是奇数,根据奇数×奇数=奇数,据此解答。
【详解】3333×7777+5555
=1111×(3333×7+5)
=1111×(23331+5)
=1111×23336
1111是奇数,23336是偶数,则3333×7777+5555的结果是偶数。
【点睛】利用乘法分配律以及奇数和偶数的运算性质进行解答。
29. 2 6 18 8
【分析】此题实际上通过解方程求出□,○,△,☆代表的数,据此解答。
【详解】(1)□+5=13-6
解:□+5=7
□+5-5=7-5
□=2
(2)28-○=15+7
解:28-○=22
28-○+○-22=22+○-22
○=6
(3)3×△=54
解:3×△÷3=54÷3
△=18
(4)56÷☆=7
解:56÷☆×☆=7×☆
7×☆÷7=56÷7
☆=8
【点睛】等式的性质是解方程的主要依据,计算时要认真,不要出错。
30.;;
【分析】1分=60秒;1分米=10厘米;1吨=1000千克;低级单位换算成高级单位,除进率;再根据分数和除法的关系,分子相当于被除数,分母相当于除数,改写成分数的形式。据此解答。
【详解】49秒=49÷60=分
7厘米=7÷10=分米
13千克=13÷1000=吨
【点睛】熟记进率是解答本题的关键。
31. 2 6.88
【详解】略
32. 3m 30
【分析】根据三个连续偶数每相邻的两个偶数相差是2,如果中间的数是m,那么最小数是m-2,最大的数是m+2,然后求出这三个连续自然数的和是3m;如果这三个数的和是84,可得:3m=84,求出m的值,再加2即可求出最大数。
【详解】m-2+m+m+2
=3m+(2-2)
=3m+0
=3m
当这三个数的和是84时,可得:
3m=84
3m÷3=84÷3
m=28
28+2=30
所以,三个连续偶数,如果中间的数是m,那么这三个数的和是3m;如果这三个数的和是84,那么最大数是30。
【点睛】本题考查偶数的运算性质,关键是理解相邻两个偶数相差是2。
33.;
【分析】12枝铅笔,求每枝铅笔是铅笔总数的几分之几,用1÷12解答;
12枝铅笔,平均分给2个同学,求每人分得的铅笔是铅笔总数的几分之几,用1÷2解答。
【详解】1÷12=
1÷2=
答:每枝铅笔是铅笔总数的,每人分得的铅笔是铅笔总数的。
故答案为:;
【点睛】本题考查分数的意义及应用,求一个数是另一个数的几分之几,用除法解答。
34. 0.7 0.75
【分析】把题目中的分数化成小数,按照小数大小比较方法,比较即可。
【详解】=0.875;=0.75
>0.75=>0.7
所以最大的是,最小的是0.7,相等的是0.75和。
【点睛】此题主要考查分数、小数的互化,把分数化成小数,用分子除以分母商用小数表示即可。
35.16.56
【分析】拼成的长方形的两个长是圆的周长,宽是圆的半径,据此求出长方形的周长。
【详解】2×3.14×2+2×2
=12.56+4
=16.56(厘米)
【点睛】解答此题的关键是明白:拼成的长方形的两个长是圆的周长,宽是圆的半径。
36.(1) 30 20
(2)
【分析】(1)根据减法的意义,用减法解答。
(2)根据速度=路程÷时间,列式解答即可。
【详解】(1)45-15=30(分钟)
65-45=20(分钟)
(2)5÷15=(千米/分)
【点睛】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
37. 4 56
【分析】求最大公因数也就是这几个数的公有质因数的连乘积;最小公倍数是共有质因数与独有质因数的连乘积;首先把8和28分解质因数,即可得解。
【详解】因为8=2×2×2,
28=2×2×7,
所以8和28的最大公因数是2×2=4,最小公倍数是2×2×2×7=56。
【点睛】此题主要考查求两个数的最大公因数与最小公倍数的方法:两个数的公有质因数连乘积是最大公因数;两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数。
38.12
【分析】半径为1分米,则圆片直径为1×2=2分米,然后按长和宽分别算出能截取多少个这样的圆片,然后两者相乘。按长截取9÷2=4.5个,用去尾法保留整数是4个,按宽截取6÷2=3个,再用4×3即可。
【详解】长能截取:9÷2=4.5≈4(个)
宽能截取:6÷2=3(个)
4×3=12(个)
即,在一张长9分米,宽6分米的长方形铁皮上,截取半径1分米的小圆片。最多能截12个。
39. 折线 条形
【分析】条形统计图,从图中直观地看出数量的多少,便于比较;折线统计图不仅能看清数量的多少,还能反映数量的增减变化情况,据此解答。
【详解】要想统计某位病人在患有新冠肺炎时体温白天的变化情况,应选用(折线)统计图,要想知道全国各省一天新冠肺炎病人出院人数多少,应选用(条形)统计图。
故答案为:折线;条形
【点睛】条形统计图、折线统计图的特点是解答此题的关键,学生应牢记。
40.145
【分析】将140分解质因数:140=22 ×5×7;a、b的最小公倍数是140,表示a、b都是由2、2、5、7这四个质因数组合而成的,a、b的最大公约数是5,表示a、b都含有质因数5,且其中一个就是5(“最大”公约数是5);要取a+b的最大值,则另一个数要尽可能的大,所以,另一个数应该是140,那么a+b的最大值就是5+140=145。
【详解】由分析知:a和b其中一个是140,一个是5,所以:a+b的最大值就是5+140=145;
故答案为145。
【点睛】解答此题应先进行分解质因数,然后结合题意,根据最大公约数和最小公倍数的知识进行解答。
41. < > >
【分析】真分数<1;分数和小数比大小,将分数化成小数再比较,分数化小数,直接用分子÷分母即可;异分母分数比较大小,先通分再比较。
【详解】<4;
=6÷7≈0.86,>0.8;
、,>。
42.
【分析】根据题意,求已修的是剩下的几分之几,用除法,即12÷11,求剩下的是已修的几分之几,用除法,11÷12;已修的占整条公路的几分之几,即12÷(12+11),据此解答。
【详解】(1)12÷11=;
(2)11÷12=;
(3)12÷(12+11)
=12÷23
=
【点睛】此题主要考查学生对分数除法的实际应用解答能力,即求一个数是另一个数的几分之几,用除法。
43.(1)小强
(2) 快 慢 慢 快
(3) 小刚 3.5 小强
【分析】通过观察折线统计图完成的解答。
(1)由图可得,一样的路程小刚用时约5.5分,小强用时约4.3分,由此可知小强用时较少,因此小强最先到达终点;
(2)观察统计图可知小刚用了约1.4分便跑完400米,小强用时2.5分,由此可知前面路程中小刚跑得较快。在后一半路程中小刚到达终点时为5.5分,小强为4.3分,由此可解;
(3)由第二小题可知开赛初小刚领先,到3.5分时,小刚和小强有交集,之后小强的线是匀速上升,所以小强领先。
【详解】(1)小强先到达终点。
(2)请用“快”、“慢”来描述他们的比赛情况:小刚是先快后慢,小强是先慢后快。
(3)开赛初小刚领先,开赛3.5分后小强领先。
【点睛】本题考查通过观察折线统计图,解决实际问题。
44. < > >
【分析】根据异分母分数比较大小的方法,把异分母分数化成分母相同的分数,再根据同分母分数比较大小的方法比较大小;第一小题据此解答;
把分数化成小数,再根据小数比较大小的方法,比较大小;第二小题据此解答;
根据同分子分数比较大小的方法,分母越大,分数越小;第三小题据此解答。
【详解】和
=;=
因为<,所以<
和0.83
≈0.8333
因为0.8333>0.83,所以>0.83
和(a为非0自然数)
因为a<a+1,所以>
【点睛】利用异分母分数比较大小,分数化小数,小数比较大小,以及同分子分数比较大小的方法,进行解答。
45. 7dm 43.96dm 153.86dm2 3.5cm 7cm 38.465cm2
【分析】根据直径=半径×2、C=πd=2πr、S=πr2,代入数据计算即可。
【详解】14÷2=7(dm)
3.14×14=43.96(dm)
3.14×72=153.86(dm2)
21.98÷3.14=7(cm)
7÷2=3.5(cm)
3.14×3.52=38.465(cm2)
故答案为:7dm;43.96dm;153.86dm2;3.5cm;7cm;38.465cm2
【点睛】本题主要考查圆的半径、直径的关系及圆的周长、面积公式,认真计算即可。
46.圆的周长和它直径的比值,π,无限不循环,3.14
【详解】试题分析:根据教材中关于圆周率的含义:圆的周长和它直径的比值,叫做圆周率,圆周率用“π”表示,它是一个 无限不循环小数,保留两位小数后的近似值是3.14,解答即可.
解:圆的周长和它直径的比值叫做圆周率,用字母π表示,它是一个无限不循环小数,保留两位小数约为3.14.
故答案为圆的周长和它直径的比值,π,无限不循环,3.14.
点评:此题考查的是圆周率的知识,应多注意基础知识的理解和掌握.
47.23
【分析】设他的鞋长是x厘米,根据码和厘米的换算公式列方程即可解答。
【详解】解:设他的鞋长是x厘米。
2x-10=36
2x=46
x=23
【点睛】本题考查列方程解应用题。根据题中的等量关系式即可列出方程。
48. b a 1 ab
【分析】a、b为不是0的自然数。若a÷b=3,可知a和b是倍数关系,它们的最大公因数是较小数,最小公倍数是较大数;若a=b+1,说明a和b是连续的自然数,也就是互质数,则它们的最大公因数是1,最小公倍数是两个数的乘积,据此填空。
【详解】a、b为不是0的自然数。若a÷b=3,则a,b的最大公因数是b,最小公倍数是a。若a=b+1,则a,b的最大公因数是1,最小公倍数是ab。
【点睛】此题考查了求最大公因数和最小公倍数的方法,注意两个数互质或是倍数关系时的特殊求法。
49.1、7、13、91
【详解】试题分析:根据求一个数的因数的方法,依次进行列举即可.
解:91的因数有:1、7、13、91.
故答案为1、7、13、91.
点评:考查的是求一个数因数的方法,应有顺序的写,做到不重复,不遗漏.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.图中黑棋子占棋子总数的。如果增加1枚黑棋子,那么黑棋子占棋子总数的;如果增加1枚白棋子,黑棋子占棋子总数的。
2.在14、6、15、24中, 是 的因数, 是 的倍数.
3.图中阴影部分表示( )吨。
4.甲、乙两人骑摩托车同时从一个地点向相反方向开出,3小时后两人相距240千米。已知乙的速度是35千米/时,甲的速度是( )千米/时。
5.把质量为3千克的西瓜平均切成8块,每块西瓜重( )千克,每块西瓜的质量占西瓜总质量的( ).
6.用5千克黄豆可制成豆腐22千克,每千克黄豆可制豆腐千克,每千克豆腐需要黄豆千克。
7.甲数的最大因数是36,乙数的最小倍数是24,甲乙两数的最大公因数是( ),最小公倍数是( )。
8.填空:在同一圆内,半径与直径都有 条,半径的长度是直径的 ,直径与半径的长度比是 .
9.一个四位数千位是最小的奇数,百位是最小的合数,十位是最小的质数,其它数位上是0,这个数写作 ,它既是 又是 的倍数.
10.的分子加上4,为使分数的大小不变,分母应加上 。
11.在同一个圆里,周长是直径的 倍.
12.将一个圆平均分成32等份后拼成一个近似的长方形。如果测得这个长方形的长为6.28分米,那么原来的圆的面积是( )平方分米,长方形的周长是( )分米。
13.。
14.用长3厘米、宽2厘米的长方形能够拼成图( )正方形(填序号)。我是这样想的:( )。
15.从0、3、5、8这四个数字中选两个数字组成一个两位数:( )既是5的倍数,又是3的倍数;最大的偶数是( );最小的奇数是( ),写出一个质数( )。
16.10是10的 数,也是10的 数.
17.用边长是( )分米、( )分米或( )分米的正方形瓷砖,都能正好铺满一个长16分米、宽12分米的长方形墙面,而且不需要切割。
18.五年级学生分组举行“我的中国梦”科技比赛。如果五(1)班学生每组5人或每组8人都少3人,五(1)班最少有( )名学生。
19.如果a÷b=6(ab为非0自然数),那么a和b的最大公因数是( ),最小公倍数是( )。
20.a是大于0的自然数。当a=( )时,是最大的真分数;当a=( )时,是最小的假分数。
21.在括号里填最简分数。
80厘米=( )米 25秒=( )分 60千克=( )吨
22.用圆规画圆, 决定圆的位置, 决定圆的大小。画周长是15.7cm的圆,圆规两脚间的距离应是 cm。
23.27和9的最大公因数是( );34和51的最小公倍数是( )。
24.某班的学生接近50人。在一次数学竞赛中,该班学生人数的获得一等奖,获得二等奖,获得三等奖,这个班的学生可能是 人。
25.已知2 3=2+3+4=9,5 4=5+6+7+8=26,若x 3=15,则x=( )
26.在既是2,3的倍数,又是5的倍数的数中,最大的两位数是( ),最大的三位数是( )。
27.把三根长分别是60厘米、36厘米、24厘米的绳子剪成同样长的小段,没有剩余,每段最长是( )厘米,此时共有( )小段。
28.3333×7777+5555的结果是( )(填“奇数”或“偶数”)。
29.下列算式中,□,○,△,☆各代表什么数?
(1)□+5=13-6;(2)28-○=15+7;(3)3×△=54;(4)56÷☆=7
□= ,○= ,△= ,☆= 。
30.49秒=分 7厘米=分米 13千克=吨
31.一个长方形的长是8厘米,宽是4厘米.在这个长方形里画直径4厘米的圆,最多能画( )个,剩下部分的面积是( )平方厘米.
32.三个连续偶数,如果中间的数是m,那么这三个数的和是( );如果这三个数的和是84,那么最大数是( )。
33.有12枝铅笔,平均分给2个同学。每枝铅笔是铅笔总数的,每人分得的铅笔是铅笔总数的 。
34.在0.75、、、0.7四个数中,最大的是( ),最小的是( ),相等的是( )和( )。
35.如图,将一个半径2厘米的圆形纸片平均分成若干份,剪开后拼成一个近似的长方形,拼成的近似长方形的周长是( )厘米。
36.小华骑车从家出发,去离家5千米远的书店买书,然后再骑车回家。如图表示这段时间小华离家距离的变化情况。
(1)小华在书店待了( )分钟,回家路上用了( )分钟。
(2)小华从家去书店平均每分钟行( )千米。
37.8和28的最大公因数是 ,最小公倍数是 。
38.在一张长9分米,宽6分米的长方形铁皮上,截取半径1分米的小圆片。最多能截( )个。
39.要想统计某位病人在患有新冠肺炎时体温白天的变化情况,应选用( )统计图,要想知道全国各省一天新冠肺炎病人出院人数多少,应选用( )统计图。
40.自然数a和b的最小公倍数是140,最大公约数是5,则a+b的最大值是 。
41.在括号里填>”“<”或“=”。
( )4 ( )0.8 ( )
42.一条公路,已修了12千米,还剩下11千米。已修的是剩下的( )。剩下的是已修的( ),已修了这条公路的( )。
43.看图回答问题。
(1)( )先到达终点。
(2)请用“快”、“慢”来描述他们的比赛情况:小刚是先( )后( ),小强是先( )后( )。
(3)开赛初( )领先,开赛( )分后( )领先。
44.在横线上里填上“>”“<”或“=”。
0.83 (a为非0自然数)
45.填表。
半径(r) 直径(d) 周长(C) 面积(S)
( ) 14dm ( ) ( )
( ) ( ) 21.98cm ( )
46. 叫做圆周率,用字母 表示,它是一个 小数,保留两位小数约为 .
47.鞋的尺码是指鞋底的长度,通常用“码”或“厘米”作单位。码和厘米可以用下面的公式换算:厘米数×2-10=码数。张华穿36码的鞋,他的鞋长是( )厘米。
48.a、b为不是0的自然数。若a÷b=3,则a,b的最大公因数是( ),最小公倍数是( )。若a=b+1,则a,b的最大公因数是( ),最小公倍数是( )。
49.91的所有因数有: .
《五年级暑假专项训练:填空题(含解析)-2024-2025学年下学期小学数学苏教版》参考答案
1.;;
【分析】黑棋子有5枚,棋子总数有15枚,求黑棋子占棋子总数的几分之几用除法;增加1枚黑棋子,黑棋子有(5+1)枚,棋子总数有(15+1)枚,求黑棋子占棋子总数的几分之几用除法;增加1枚白棋子,黑棋子有5枚,棋子总数有(15+1)枚,求黑棋子占棋子总数的几分之几用除法;据此解答。
【详解】5÷15=
(5+1)÷(15+1)
=6÷16
=
5÷(15+1)
=5÷16
=
【点睛】本题主要考查求一个数是另一个数的几分之几,用除法,解题时注意总数的变化。
2.6,24,24,6
【详解】试题分析:一个整数除以一个不为0的整数,得到的商是整数,而没有余数,就说一个数是另一个数的倍数,另一个数就是一个数的因数,据此解答即可.
解:因为24÷6=4,说明6是24的因数,24是6的倍数.
故答案为6,24,24,6.
点评:此题主要考查约数与倍数的意义及其运用.
3.
【分析】观察图形,把3吨的整体平均分成了4份,阴影部分占其中一份,要计算这一份是多少应该用3除以4,根据分数与除法的关系可知,计算结果为。
【详解】3÷4=(吨)
图中阴影部分表示吨。
4.45
【分析】根据题意,甲、乙两车同时从一个地点向相反的方向开出3小时后相距240千米,也就是甲乙两人行驶的总路程等于240千米;甲的速度加乙的速度是速度和,它们之间的数量关系是速度和×时间=总路程。可以假设甲的速度是x千米/时,根据数量关系列式解答即可。
【详解】解:设甲的速度是x千米/时。
(x+35)×3=240
(x+35)×3÷3=240÷3
x+35=80
x+35-35=80-35
x=45
甲的速度是45千米/时。
5.
【详解】略
6.;
【分析】用豆腐的质量除以黄豆的质量,即可求出每千克黄豆克制豆腐多少千克;用黄豆的质量除以豆腐的质量,即可求出每千克豆腐需要黄豆多少千克,即可解答。
【详解】22÷5=(千克)
5÷22=(千克)
【点睛】本题考查分数的意义,关键是找清楚谁是单一量,然后把另一个量进行平均分。
7. 12 72
【分析】一个数的最大因数是它本身;一个数的最小倍数是它本身。据此可得:甲数是36,乙数是24。
用质因数分解法可以求两个数的最大公因数和最小公倍数。全部共有的质因数(公有质因数)相乘的积就是这两个数的最大公因数;全部公有的质因数和各自独立的质因数,它们连乘的积就是这两个数的最小公倍数。据此解答。
【详解】通过分析可得:甲数是36,乙数是24。
36=2×2×3×3
24=2×2×2×3
则甲乙两数的最大公因数是2×2×3=12,最小公倍数是2×2×3×2×3=72。
8.无数,一半,2:1
【详解】试题分析:在同一圆内,直径的长度是半径的两倍,由此进行做题.
解:由题意知,在同一圆内,半径与直径都有无数条,半径的长度是直径的一半,直径与半径的长度比是2:1.
故答案为无数,一半,2:1.
点评:此题考查了在同一圆内圆的半径和直径的关系.
9.1420,2的倍数,5
【详解】试题分析:(1)最小的奇数是1,最小的合数是4,最小的质数是2;可知这个四位数的千位上是1,百位上是4,十位上是2,个位上是0,写出此数即可;
(2)能被2整除的数的特征:个位上是0、2、4、6、8;能被5整除的数的特征:个位上是0或5,据此进行判断.
解;(1)最小的奇数是1,最小的合数是4,最小的质数是2,所以这个四位数写作:1420;
(2)1420的个位上是0,所以1420既是2的倍数又是5的倍数.
故答案为1420,2的倍数,5.
点评:解答本题要明确奇数、质数、合数的概念和能被2、5整除的数的特征.
10.18
【详解】原分数分子是2,现在分数的分子是2+4=6,扩大3倍,即
9×3=27
27-9=18
分母应加上18。
【点睛】此题主要利用分数的基本性质解答问题,先观察分子或分母之间的变化,发现规律,再进一步通过计算解答问题。
11.π
【分析】根据圆周率的含义:圆周率等于圆的周长和它直径的比值,用字母“π”表示;由此解答即可.
【详解】根据圆周率的含义可知:圆周长总是它直径长度的π倍,π取近似值为3.14;
故答案为π.
12. 12.56 16.56
【分析】将一个圆拼成一个近似的长方形,长方形的长=圆周长的一半(πr),长方形的宽=圆的半径(r)。由长方形的长为6.28分米,可求得圆的半径(宽),根据圆的面积公式代入数据即可求得圆的面积,根据长方形的周长=(长+宽)×2代入数据即可求得长方形的周长。
【详解】半径:6.28÷3.14=2(分米)
圆的面积:3.14×22=12.56(平方分米)
长方形的周长:(6.28+2)×2
=8.28×2
=16.56(分米)
故答案为:12.56;16.56
【点睛】本题主要考查圆的面积公式,解题的关键是理解“将一个圆拼成一个近似的长方形,长方形的长=圆周长的一半,长方形的宽=圆的半径”。
13.1;10;3
【分析】根据小数化分数的方法先将0.5化成分数,再根据分数的基本性质即分数与除法的关系填空即可。
【详解】;
;
即
【点睛】熟练掌握小数化分数的方法、分数的基本性质、分数与除法的关系是解题关键。
14. ② 用长3厘米、宽2厘米的长方形拼成正方形,正方形的边长既是3的倍数也是2的倍数,12既是3的倍数也是2的倍数,所以可以拼成边长是12厘米的正方形
【分析】用长3厘米、宽2厘米的长方形拼成正方形,正方形的边长既是3的倍数也是2的倍数,12既是3的倍数也是2的倍数,所以可以拼成边长是12厘米的正方形,能够拼成图②正方形,据此解答即可。
【详解】用长3厘米、宽2厘米的长方形能够拼成图②正方形。我是这样想的:用长3厘米、宽2厘米的长方形拼成正方形,正方形的边长既是3的倍数也是2的倍数,12既是3的倍数也是2的倍数,所以可以拼成边长是12厘米的正方形。(答案不唯一,合理即可)
【点睛】本题考查最小公倍数,解答本题的关键是掌握最小公倍数的概念。
15. 30 80 35 53
【分析】既是3的倍数又是5的倍数的特征:个位上的数字是0或5,各个数位上的数字的和是3的倍数的数。整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。一个大于1的自然数,除了1和它本身以外不再有其他因数,这样的数叫质数。一个大于1的自然数,除了1和它本身以外还有其他因数,这样的数叫合数。组成的两位数是质数的有53、83。据此解答。
【详解】从0、3、5、8这四个数字中选两个数字组成一个两位数:30既是5的倍数,又是3的倍数;最大的偶数是80;最小的奇数是35,写出一个质数53。
16.因,倍
【详解】试题分析:根据一个数的因数是有限的,其中最大的因数是它本身,一个数的倍数的个数是无限的,其中最小的倍数是它本身,据此解答.
解:10是10的因数,也是10的倍数;
故答案为因,倍.
点评:本题主要考查因数倍数的意义,注意个数的最大的因数是它本身,一个数的最小的倍数是它本身.
17. 1 2 4
【分析】正方形瓷砖刚好铺满长方形的墙面,可得正方形的边长应该是长方形长和宽的公因数,找出16和12的公因数即可。
【详解】16的因数有:1,2,4,8,16;
12的因数有:1,2,3,4,6,12;
所以16和12的公因数有:1,2,4
【点睛】此题考查了两个数公因数的求法,关键是要理解正方形瓷砖的边长是长方形长和宽的公因数。
18.37
【分析】由题意可知,五(1)班的人数是5和8的最小公倍数减3,据此解答。
【详解】5和8互质,它们的最小公倍数是5×8=40,40-3=37(人),五(1)班最少有37人。
【点睛】此题主要考查最小公倍数的实际应用,注意少3人,记得最后减3。
19. b a
【分析】两个数为倍数关系,则最大公因数是较小的数,最小公倍数为较大的数;两个数互质,则最大公因数是1。
【详解】因为a÷b=6(a、b为非0自然数),所以a与b的最大公因数为b,最小公倍数为a。
【点睛】熟练掌握求两个数最大公因数与最小公倍数的方法是解题的关键。
20. 7 6
【分析】分子比分母小的分数叫做真分数。分子比分母大或分子和分母相等的分数叫做假分数。
分数大小的比较:分母相同时,分子越大,分数值就越大;分子相同时,分母越大,分数值反而越小。
【详解】是真分数,则a>6;因为>>>……,所以当a=7时,是最大的真分数。
是假分数,则a≥6;因为<<<<……,所以当a=6时,是最小的假分数。
21.
【分析】根据1米=100厘米,1分=60秒,1吨=1000千克,单位小变大除以进率,用小单位数据÷进率,根据分数与除法的关系,即分数的分子相当于被除数,分母相当于除数,表示出结果,约分即可。
【详解】80÷100==(米)
25÷60==(分)
60÷1000==(吨)
22. 圆心 半径 2.5
【分析】根据圆心决定圆的位置;半径决定圆的大小;圆规两脚间的距离是圆的半径,再根据圆的周长公式:周长=2πr,求出圆的半径,即可。
【详解】周长是15.7cm圆的半径:15.7÷3.14÷2
=5÷2
=2.5(厘米)
用圆规画圆,圆心决定圆的位置,半径决定圆的大小。画周长是15.7cm的圆,圆规两脚间的距离应是2.5cm。
【点睛】本题考查圆的特点,应注重基础知识的理解和运用。
23. 9 102
【分析】两个数的最大公因数是两个数的公有质因数的连乘积;两个数的最小公倍数是两个数的公有质因数与每一个数独有质因数的连乘积;如果两个数为倍数关系,较小的数为最大公因数;较大的那个数为最小公倍数;如果两个数为互质数,最大公因数是1,最小公倍数是两个数的乘积,据此解答。
【详解】27是9的倍数,27和9的最大公因数是9;
34=2×17
51=3×17
34和51的最小公倍数是2×3×17=102
27和9的最大公因数是9;34和54的最小公倍数是102。
【点睛】熟练掌握最大公因数和最小公倍数的求法是解答本题的关键。
24.36
【分析】根据题意可知,这个班的人数一定是这几个分数分母的公倍数,先求出这几个分数分母的最小公倍数,然后与条件中的50人对比即可解答。
【详解】12=3×2×2;
4=2×2;
9=3×3;
12、4、9的最小公倍数是3×2×2×3=36;
36接近50,这个班的学生可能是36人。
【点睛】本题主要考查公倍数的应用,理解班级人数是12、4、9的公倍数是解题的关键。
25.4
【分析】观察等式,可知2 3表示从2开始,3个连续自然数的和,5 4表示从5开始,4个连续自然数的和,由此可知x 3表示从x开始,3个连续自然数的和,据此列方程求解即可。
【详解】由x 3=15,得:
x+(x+1)+(x+2)=15
3x+3=15
3x=12
x=4
故答案为:4。
【点睛】本题考查定义新运算,关键是根据已知等式,正确理解新定义的运算规则。
26. 90 990
【分析】个位上是0,2,4,6或8的数,都是2的倍数。个位上是0或5的数,都是5的倍数。一个数各位上的数的和是3的倍数,这个数就是3的倍数。既是2和3的倍数,又是5的倍数,这个数的个位上的数字是0,各个数位上的数字的和是3的倍数。
【详解】在既是2,3的倍数,又是5的倍数的数中,最大的两位数是90,最大的三位数是990。
27. 12 10
【分析】求每段最长几厘米,就是求出这三根绳子长度的最大公因数,由此可以解决问题。用60、36和24分别除以它们的最大公因数的和就是一共能剪成多少段。
【详解】60、36、24的最大公因数是12,所以每段最长是12厘米。
60÷12+36÷12+24÷12
=5+3+2
=8+2
=10(段)
此时共有10小段。
【点睛】此题考查了求几个数的最大公因数在实际问题中的灵活应用,由此可以解决问题。
28.偶数
【分析】把3333×7777+5555化为:1111×(3333×7+5);计算出3333×7+5的结果,如果结果是偶数,那么根据奇数×偶数=偶数;如果结果是奇数,根据奇数×奇数=奇数,据此解答。
【详解】3333×7777+5555
=1111×(3333×7+5)
=1111×(23331+5)
=1111×23336
1111是奇数,23336是偶数,则3333×7777+5555的结果是偶数。
【点睛】利用乘法分配律以及奇数和偶数的运算性质进行解答。
29. 2 6 18 8
【分析】此题实际上通过解方程求出□,○,△,☆代表的数,据此解答。
【详解】(1)□+5=13-6
解:□+5=7
□+5-5=7-5
□=2
(2)28-○=15+7
解:28-○=22
28-○+○-22=22+○-22
○=6
(3)3×△=54
解:3×△÷3=54÷3
△=18
(4)56÷☆=7
解:56÷☆×☆=7×☆
7×☆÷7=56÷7
☆=8
【点睛】等式的性质是解方程的主要依据,计算时要认真,不要出错。
30.;;
【分析】1分=60秒;1分米=10厘米;1吨=1000千克;低级单位换算成高级单位,除进率;再根据分数和除法的关系,分子相当于被除数,分母相当于除数,改写成分数的形式。据此解答。
【详解】49秒=49÷60=分
7厘米=7÷10=分米
13千克=13÷1000=吨
【点睛】熟记进率是解答本题的关键。
31. 2 6.88
【详解】略
32. 3m 30
【分析】根据三个连续偶数每相邻的两个偶数相差是2,如果中间的数是m,那么最小数是m-2,最大的数是m+2,然后求出这三个连续自然数的和是3m;如果这三个数的和是84,可得:3m=84,求出m的值,再加2即可求出最大数。
【详解】m-2+m+m+2
=3m+(2-2)
=3m+0
=3m
当这三个数的和是84时,可得:
3m=84
3m÷3=84÷3
m=28
28+2=30
所以,三个连续偶数,如果中间的数是m,那么这三个数的和是3m;如果这三个数的和是84,那么最大数是30。
【点睛】本题考查偶数的运算性质,关键是理解相邻两个偶数相差是2。
33.;
【分析】12枝铅笔,求每枝铅笔是铅笔总数的几分之几,用1÷12解答;
12枝铅笔,平均分给2个同学,求每人分得的铅笔是铅笔总数的几分之几,用1÷2解答。
【详解】1÷12=
1÷2=
答:每枝铅笔是铅笔总数的,每人分得的铅笔是铅笔总数的。
故答案为:;
【点睛】本题考查分数的意义及应用,求一个数是另一个数的几分之几,用除法解答。
34. 0.7 0.75
【分析】把题目中的分数化成小数,按照小数大小比较方法,比较即可。
【详解】=0.875;=0.75
>0.75=>0.7
所以最大的是,最小的是0.7,相等的是0.75和。
【点睛】此题主要考查分数、小数的互化,把分数化成小数,用分子除以分母商用小数表示即可。
35.16.56
【分析】拼成的长方形的两个长是圆的周长,宽是圆的半径,据此求出长方形的周长。
【详解】2×3.14×2+2×2
=12.56+4
=16.56(厘米)
【点睛】解答此题的关键是明白:拼成的长方形的两个长是圆的周长,宽是圆的半径。
36.(1) 30 20
(2)
【分析】(1)根据减法的意义,用减法解答。
(2)根据速度=路程÷时间,列式解答即可。
【详解】(1)45-15=30(分钟)
65-45=20(分钟)
(2)5÷15=(千米/分)
【点睛】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
37. 4 56
【分析】求最大公因数也就是这几个数的公有质因数的连乘积;最小公倍数是共有质因数与独有质因数的连乘积;首先把8和28分解质因数,即可得解。
【详解】因为8=2×2×2,
28=2×2×7,
所以8和28的最大公因数是2×2=4,最小公倍数是2×2×2×7=56。
【点睛】此题主要考查求两个数的最大公因数与最小公倍数的方法:两个数的公有质因数连乘积是最大公因数;两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数。
38.12
【分析】半径为1分米,则圆片直径为1×2=2分米,然后按长和宽分别算出能截取多少个这样的圆片,然后两者相乘。按长截取9÷2=4.5个,用去尾法保留整数是4个,按宽截取6÷2=3个,再用4×3即可。
【详解】长能截取:9÷2=4.5≈4(个)
宽能截取:6÷2=3(个)
4×3=12(个)
即,在一张长9分米,宽6分米的长方形铁皮上,截取半径1分米的小圆片。最多能截12个。
39. 折线 条形
【分析】条形统计图,从图中直观地看出数量的多少,便于比较;折线统计图不仅能看清数量的多少,还能反映数量的增减变化情况,据此解答。
【详解】要想统计某位病人在患有新冠肺炎时体温白天的变化情况,应选用(折线)统计图,要想知道全国各省一天新冠肺炎病人出院人数多少,应选用(条形)统计图。
故答案为:折线;条形
【点睛】条形统计图、折线统计图的特点是解答此题的关键,学生应牢记。
40.145
【分析】将140分解质因数:140=22 ×5×7;a、b的最小公倍数是140,表示a、b都是由2、2、5、7这四个质因数组合而成的,a、b的最大公约数是5,表示a、b都含有质因数5,且其中一个就是5(“最大”公约数是5);要取a+b的最大值,则另一个数要尽可能的大,所以,另一个数应该是140,那么a+b的最大值就是5+140=145。
【详解】由分析知:a和b其中一个是140,一个是5,所以:a+b的最大值就是5+140=145;
故答案为145。
【点睛】解答此题应先进行分解质因数,然后结合题意,根据最大公约数和最小公倍数的知识进行解答。
41. < > >
【分析】真分数<1;分数和小数比大小,将分数化成小数再比较,分数化小数,直接用分子÷分母即可;异分母分数比较大小,先通分再比较。
【详解】<4;
=6÷7≈0.86,>0.8;
、,>。
42.
【分析】根据题意,求已修的是剩下的几分之几,用除法,即12÷11,求剩下的是已修的几分之几,用除法,11÷12;已修的占整条公路的几分之几,即12÷(12+11),据此解答。
【详解】(1)12÷11=;
(2)11÷12=;
(3)12÷(12+11)
=12÷23
=
【点睛】此题主要考查学生对分数除法的实际应用解答能力,即求一个数是另一个数的几分之几,用除法。
43.(1)小强
(2) 快 慢 慢 快
(3) 小刚 3.5 小强
【分析】通过观察折线统计图完成的解答。
(1)由图可得,一样的路程小刚用时约5.5分,小强用时约4.3分,由此可知小强用时较少,因此小强最先到达终点;
(2)观察统计图可知小刚用了约1.4分便跑完400米,小强用时2.5分,由此可知前面路程中小刚跑得较快。在后一半路程中小刚到达终点时为5.5分,小强为4.3分,由此可解;
(3)由第二小题可知开赛初小刚领先,到3.5分时,小刚和小强有交集,之后小强的线是匀速上升,所以小强领先。
【详解】(1)小强先到达终点。
(2)请用“快”、“慢”来描述他们的比赛情况:小刚是先快后慢,小强是先慢后快。
(3)开赛初小刚领先,开赛3.5分后小强领先。
【点睛】本题考查通过观察折线统计图,解决实际问题。
44. < > >
【分析】根据异分母分数比较大小的方法,把异分母分数化成分母相同的分数,再根据同分母分数比较大小的方法比较大小;第一小题据此解答;
把分数化成小数,再根据小数比较大小的方法,比较大小;第二小题据此解答;
根据同分子分数比较大小的方法,分母越大,分数越小;第三小题据此解答。
【详解】和
=;=
因为<,所以<
和0.83
≈0.8333
因为0.8333>0.83,所以>0.83
和(a为非0自然数)
因为a<a+1,所以>
【点睛】利用异分母分数比较大小,分数化小数,小数比较大小,以及同分子分数比较大小的方法,进行解答。
45. 7dm 43.96dm 153.86dm2 3.5cm 7cm 38.465cm2
【分析】根据直径=半径×2、C=πd=2πr、S=πr2,代入数据计算即可。
【详解】14÷2=7(dm)
3.14×14=43.96(dm)
3.14×72=153.86(dm2)
21.98÷3.14=7(cm)
7÷2=3.5(cm)
3.14×3.52=38.465(cm2)
故答案为:7dm;43.96dm;153.86dm2;3.5cm;7cm;38.465cm2
【点睛】本题主要考查圆的半径、直径的关系及圆的周长、面积公式,认真计算即可。
46.圆的周长和它直径的比值,π,无限不循环,3.14
【详解】试题分析:根据教材中关于圆周率的含义:圆的周长和它直径的比值,叫做圆周率,圆周率用“π”表示,它是一个 无限不循环小数,保留两位小数后的近似值是3.14,解答即可.
解:圆的周长和它直径的比值叫做圆周率,用字母π表示,它是一个无限不循环小数,保留两位小数约为3.14.
故答案为圆的周长和它直径的比值,π,无限不循环,3.14.
点评:此题考查的是圆周率的知识,应多注意基础知识的理解和掌握.
47.23
【分析】设他的鞋长是x厘米,根据码和厘米的换算公式列方程即可解答。
【详解】解:设他的鞋长是x厘米。
2x-10=36
2x=46
x=23
【点睛】本题考查列方程解应用题。根据题中的等量关系式即可列出方程。
48. b a 1 ab
【分析】a、b为不是0的自然数。若a÷b=3,可知a和b是倍数关系,它们的最大公因数是较小数,最小公倍数是较大数;若a=b+1,说明a和b是连续的自然数,也就是互质数,则它们的最大公因数是1,最小公倍数是两个数的乘积,据此填空。
【详解】a、b为不是0的自然数。若a÷b=3,则a,b的最大公因数是b,最小公倍数是a。若a=b+1,则a,b的最大公因数是1,最小公倍数是ab。
【点睛】此题考查了求最大公因数和最小公倍数的方法,注意两个数互质或是倍数关系时的特殊求法。
49.1、7、13、91
【详解】试题分析:根据求一个数的因数的方法,依次进行列举即可.
解:91的因数有:1、7、13、91.
故答案为1、7、13、91.
点评:考查的是求一个数因数的方法,应有顺序的写,做到不重复,不遗漏.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
