2.6 应用一元二次方程 同步练习(含答案)
文档属性
| 名称 | 2.6 应用一元二次方程 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 193.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-09 13:29:13 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
6 应用一元二次方程
一、单选题
1.(2024八下·临平期中)某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,为占有市场份额,且经市场调查:每降价1元,每星期可多卖出20件.现要在尽量优惠顾客情况下,同时获利6120元,每件商品应降价( )元.
A.3 B.2.5 C.2 D.2或3
2.(2024九下·福山期中)辽南是“中国苹果之乡”,某超市将进价为每千克元的苹果按每千克元卖出,平均一天能卖出千克,为了尽快减少库存,决定降价销售,超市发现当售价每千克下降元时,其日销售量就增加千克,设售价下降元,超市每天销售苹果的利润为元,则可列方程为( )
A. B.
C. D.
3.(2020九上·霸州期末)某产品成本价为100万元,由于改进技术,成本连续降低,每次降低 %,连续两次降低后成本为64万元,则 的值为( )
A.10 B.15 C.18 D.20
4.(2025九上·张家口期末)我国古代著作《四元玉鉴》中记载“买椽多少”问题,其大意为:现请人代买一批椽,这批株的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱.根据题意可列方程,其中x表示( )
A.剩余椽的数量 B.这批椽的数量
C.剩余椽的运费 D.每株椽的价钱
5.(2023九上·浏阳期中)如图,在一块长为,宽为的矩形地面内(两条道路分别与矩形的一条边平行),余下的铺上草坪,要使草坪的面积达到,设道路的宽为,可列方程为( )
A. B.
C. D.
6.(2024八下·杭州期中)《周髀算经》中有一种几何方法可以用来解形如的方程的正数解,方法为:如图,将四个长为,宽为x的长方形纸片(面积为16)拼成一个大正方形,于是大正方形的面积为,边长为10,故得的正数解为.小明用此方法解关于x的方程时,构造出同样的图形,已知大正方形的面积为14,小正方形的面积为4,则( )
A. B. C. D.
7.(2018九上·安陆月考)某市从2017年开始大力发展“竹文化”旅游产业.据统计,该市2017年“竹文化”旅游收入约为2亿元.预计2019年“竹文化”旅游输入将达到2.88亿元,据此估计该市2018年、2019年“竹文化”旅游收入的年平均增长率约为( )
A.2% B.4.4 % C.20% D.44%
8.(2021九上·津南期中)要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排21场比赛,应邀请多少个队参加比赛.设应邀请x个队参加比赛,则x的值为( )
A.7 B.8 C.9 D.10
9.(2020九上·平山期中)《代数学》中记载,形如 的方程,求正数解的几何方法是:“如图1,先构造一个面积为 的正方形,再以正方形的边长为一边向外构造四个面积为 的矩形,得到大正方形的面积为 ,则该方程的正数解为 .”小聪按此方法解关于 的方程 时,构造出如图2所示的图形,已知阴影部分的面积为36,则该方程的正数解为( )
A.6 B. C. D.
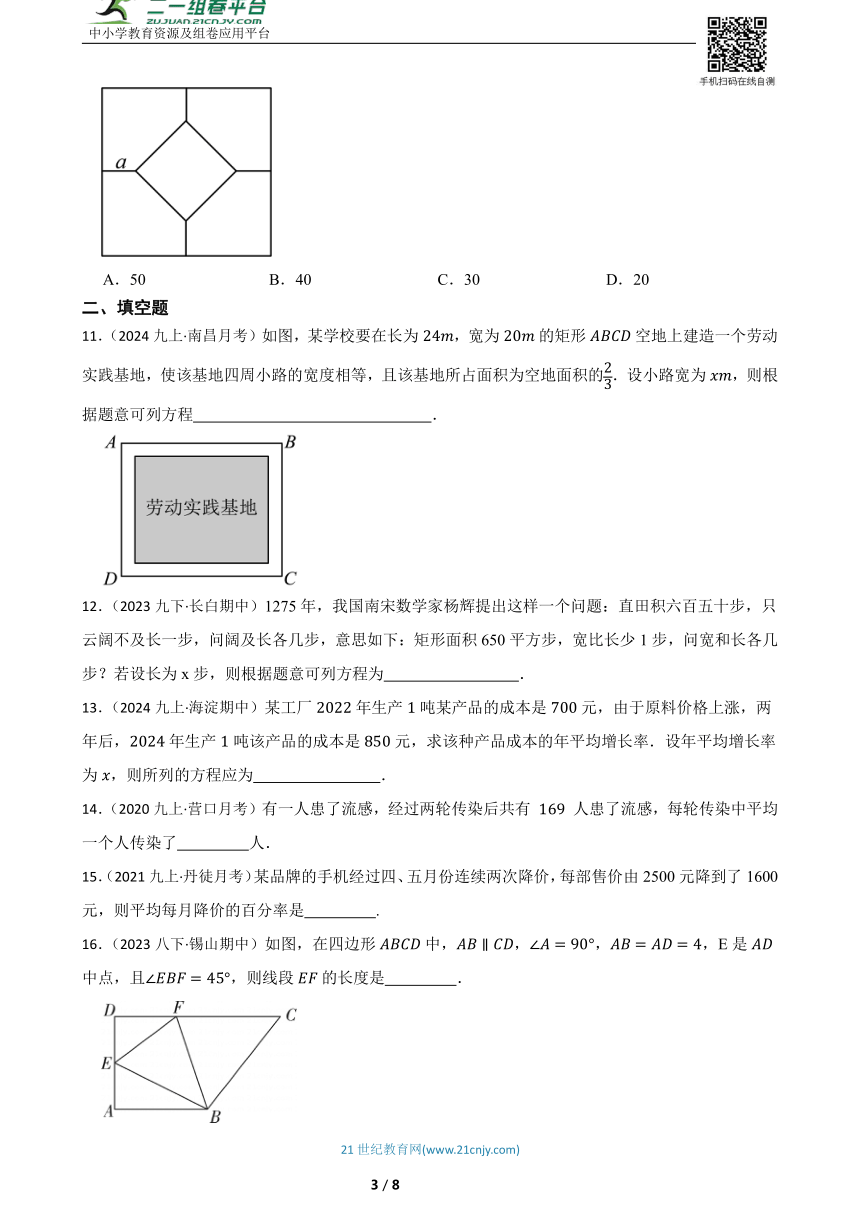
10.(2024·苏州模拟)如图,一块正方形地砖的图案是由4个全等的五边形和1个小正方形组成的,已知小正方形的面积和五边形的面积相等,并且图中线段a的长度为,则这块地砖的面积为( )
A.50 B.40 C.30 D.20
二、填空题
11.(2024九上·南昌月考)如图,某学校要在长为,宽为的矩形空地上建造一个劳动实践基地,使该基地四周小路的宽度相等,且该基地所占面积为空地面积的.设小路宽为,则根据题意可列方程 .
12.(2023九下·长白期中)1275年,我国南宋数学家杨辉提出这样一个问题:直田积六百五十步,只云阔不及长一步,问阔及长各几步,意思如下:矩形面积650平方步,宽比长少1步,问宽和长各几步?若设长为x步,则根据题意可列方程为 .
13.(2024九上·海淀期中)某工厂年生产吨某产品的成本是元,由于原料价格上涨,两年后,年生产吨该产品的成本是元,求该种产品成本的年平均增长率.设年平均增长率为,则所列的方程应为 .
14.(2020九上·营口月考)有一人患了流感,经过两轮传染后共有 人患了流感,每轮传染中平均一个人传染了 人.
15.(2021九上·丹徒月考)某品牌的手机经过四、五月份连续两次降价,每部售价由2500元降到了1600元,则平均每月降价的百分率是 .
16.(2023八下·锡山期中)如图,在四边形中,,,,E是中点,且,则线段的长度是 .
三、计算题
17.(2024九上·凉州期中)如图,把一块长为,宽为的矩形硬纸板的四角各剪去一个同样大小的正方形,再折叠成一个无盖的长方体纸盒.若该无盖纸盒的底面积为,求剪去的小正方形的边长.
18.(2024九上·即墨月考)[问题提出]:如图1,由n×n×n(长×宽×高)个小立方块组成的正方体中,到底有多少个长方体(包括正方体)呢?
[问题探究]:我们先从较为简单的情形入手.
(1)如图2,由2×1×1个小立方块组成的长方体中,长共有1+2==3条线段,宽和高分别只有1条线段,所以图中共有3×1×1=3个长方体.
(2)如图3,由2×2×1个小立方块组成的长方体中,长和宽分别有1+2==3条线段,高有1条线段,所以图中共有3×3×1=9个长方体.
(3)如图4,由2×2×2个小立方体组成的正方体中,长、宽、高分别有1+2==3条线段,所以图中共有 个长方体.
(4)由2×3×6个小立方块组成的长方体中,长共有1+2==3条线段,宽共有 条线段,高共有 条线段,所以图中共有 个长方体.
[问题解决]
(5)由n×n×n个小立方块组成的正方体中,长、宽、高各有 线段,所以图中共有 个长方体.
[结论应用]
(6)如果由若干个小立方块组成的正方体中共有3375个长方体,那么组成这个正方体的小立方块的个数是多少?请通过计算说明你的结论.
四、解答题
19.(2023九上·甘州月考)某种商品平均每天可销售60件,每件盈利100元.为了尽快减少库存,商场决定采取适当的降价措施,经调查发现,每件商品每降价1元,商场平均每天可多售出2件.据此规律,请回答:
(1)当商场日销售量为80件时,商场日盈利可达到多少元.
(2)为了尽量减少库存,每件商品降价多少元时,商场日盈利可达到8400元?
20.(2024九上·南康期中)某种服装,平均每天可销售件,每件盈利元,若每件降价元,每天可多卖件,如果每天要盈利元,每件应降价多少元?
21.(2023九上·禅城月考)某电子器件厂生产一种电脑显卡,2021年该类电脑显卡的出厂价是200元/个,2022年,2023年连续两年在技术扶贫的帮助下改进技术,降低成本,2023年该电脑显卡的出厂价调整为162元/件.
(1)这两年此类电脑显卡出厂价下降的百分率相同,求平均每年下降的百分率.
(2)2023年某赛格电脑城以出厂价购进若干个此类电脑显卡,以200元/个销售时,平均每天可销售20个.为了尽快减少库存,商场决定降价销售.经调查发现,单价每降低1元,每天可多售出2个,如果每天盈利1150元,单价应降低多少元?
22.(2023九上·青白江期中)如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED边长,易知,这时我们把关于x的形如的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于x的“勾系一元二次方程” 必有实数根;
(3)若x=﹣1是“勾系一元二次方程”的一个根,且四边形ACDE的周长是6,求△ABC面积.
答案解析部分
1.【答案】A
【知识点】一元二次方程的实际应用-销售问题
2.【答案】B
【知识点】一元二次方程的实际应用-销售问题
3.【答案】D
【知识点】一元二次方程的实际应用-百分率问题
4.【答案】B
【知识点】一元二次方程的其他应用
5.【答案】C
【知识点】列一元二次方程
6.【答案】D
【知识点】一元二次方程的应用-几何问题
7.【答案】C
【知识点】一元二次方程的实际应用-百分率问题
8.【答案】A
【知识点】一元二次方程的实际应用-传染问题
9.【答案】B
【知识点】一元二次方程的应用-几何问题
10.【答案】B
【知识点】二次根式的应用;三角形全等及其性质;正方形的性质;一元二次方程的应用-几何问题
11.【答案】
【知识点】一元二次方程的应用-几何问题
12.【答案】x(x-1)=650
【知识点】一元二次方程的应用-几何问题
13.【答案】
【知识点】一元二次方程的实际应用-百分率问题
14.【答案】12
【知识点】一元二次方程的其他应用
15.【答案】20%
【知识点】一元二次方程的实际应用-百分率问题
16.【答案】
【知识点】一元二次方程的其他应用;勾股定理;正方形的判定与性质;三角形全等的判定-SAS
17.【答案】减去的小正方形的边长为
【知识点】一元二次方程的应用-几何问题
18.【答案】(3)27;(4)21,378;(5),;(6)组成这个正方体的小立方块的个数是125个
【知识点】探索图形规律;一元二次方程的应用-几何问题
19.【答案】(1)7200
(2)每件商品降价40元,商场日盈利可8400元;
【知识点】一元二次方程的实际应用-销售问题
20.【答案】每件应降价或元
【知识点】一元二次方程的实际应用-销售问题
21.【答案】(1)解:设平均下降率为,
依题意得:,
解得:,(不合题意,舍去)
答:平均下降率为10%;
(2)解:设单价应降低元,
则每个的销售利润为元,
每天可售出个,
依题意得:,
解得:,,
∵为了减少库存,∴,
答:单价应降低15元
【知识点】一元二次方程的实际应用-百分率问题;一元二次方程的实际应用-销售问题
22.【答案】(1)解:当a=3,b=4,c=5时
勾系一元二次方程为3x2+5x+4=0;
(2)证明:根据题意,得
Δ=(c)2﹣4ab=2c2﹣4ab
∵a2+b2=c2
∴2c2﹣4ab=2(a2+b2)﹣4ab=2(a﹣b)2≥0
即△≥0
∴勾系一元二次方程必有实数根;
(3)解:当x=﹣1时,有a﹣c+b=0,即a+b=c
∵2a+2b+c=6,即2(a+b)+c=6
∴3c=6
∴c=2
∴a2+b2=c2=4,a+b=2
∵(a+b)2=a2+b2+2ab
∴ab=2
∴S△ABC=ab=1.
【知识点】一元二次方程的其他应用
21世纪教育网(www.21cnjy.com)
2 / 8
6 应用一元二次方程
一、单选题
1.(2024八下·临平期中)某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,为占有市场份额,且经市场调查:每降价1元,每星期可多卖出20件.现要在尽量优惠顾客情况下,同时获利6120元,每件商品应降价( )元.
A.3 B.2.5 C.2 D.2或3
2.(2024九下·福山期中)辽南是“中国苹果之乡”,某超市将进价为每千克元的苹果按每千克元卖出,平均一天能卖出千克,为了尽快减少库存,决定降价销售,超市发现当售价每千克下降元时,其日销售量就增加千克,设售价下降元,超市每天销售苹果的利润为元,则可列方程为( )
A. B.
C. D.
3.(2020九上·霸州期末)某产品成本价为100万元,由于改进技术,成本连续降低,每次降低 %,连续两次降低后成本为64万元,则 的值为( )
A.10 B.15 C.18 D.20
4.(2025九上·张家口期末)我国古代著作《四元玉鉴》中记载“买椽多少”问题,其大意为:现请人代买一批椽,这批株的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱.根据题意可列方程,其中x表示( )
A.剩余椽的数量 B.这批椽的数量
C.剩余椽的运费 D.每株椽的价钱
5.(2023九上·浏阳期中)如图,在一块长为,宽为的矩形地面内(两条道路分别与矩形的一条边平行),余下的铺上草坪,要使草坪的面积达到,设道路的宽为,可列方程为( )
A. B.
C. D.
6.(2024八下·杭州期中)《周髀算经》中有一种几何方法可以用来解形如的方程的正数解,方法为:如图,将四个长为,宽为x的长方形纸片(面积为16)拼成一个大正方形,于是大正方形的面积为,边长为10,故得的正数解为.小明用此方法解关于x的方程时,构造出同样的图形,已知大正方形的面积为14,小正方形的面积为4,则( )
A. B. C. D.
7.(2018九上·安陆月考)某市从2017年开始大力发展“竹文化”旅游产业.据统计,该市2017年“竹文化”旅游收入约为2亿元.预计2019年“竹文化”旅游输入将达到2.88亿元,据此估计该市2018年、2019年“竹文化”旅游收入的年平均增长率约为( )
A.2% B.4.4 % C.20% D.44%
8.(2021九上·津南期中)要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排21场比赛,应邀请多少个队参加比赛.设应邀请x个队参加比赛,则x的值为( )
A.7 B.8 C.9 D.10
9.(2020九上·平山期中)《代数学》中记载,形如 的方程,求正数解的几何方法是:“如图1,先构造一个面积为 的正方形,再以正方形的边长为一边向外构造四个面积为 的矩形,得到大正方形的面积为 ,则该方程的正数解为 .”小聪按此方法解关于 的方程 时,构造出如图2所示的图形,已知阴影部分的面积为36,则该方程的正数解为( )
A.6 B. C. D.
10.(2024·苏州模拟)如图,一块正方形地砖的图案是由4个全等的五边形和1个小正方形组成的,已知小正方形的面积和五边形的面积相等,并且图中线段a的长度为,则这块地砖的面积为( )
A.50 B.40 C.30 D.20
二、填空题
11.(2024九上·南昌月考)如图,某学校要在长为,宽为的矩形空地上建造一个劳动实践基地,使该基地四周小路的宽度相等,且该基地所占面积为空地面积的.设小路宽为,则根据题意可列方程 .
12.(2023九下·长白期中)1275年,我国南宋数学家杨辉提出这样一个问题:直田积六百五十步,只云阔不及长一步,问阔及长各几步,意思如下:矩形面积650平方步,宽比长少1步,问宽和长各几步?若设长为x步,则根据题意可列方程为 .
13.(2024九上·海淀期中)某工厂年生产吨某产品的成本是元,由于原料价格上涨,两年后,年生产吨该产品的成本是元,求该种产品成本的年平均增长率.设年平均增长率为,则所列的方程应为 .
14.(2020九上·营口月考)有一人患了流感,经过两轮传染后共有 人患了流感,每轮传染中平均一个人传染了 人.
15.(2021九上·丹徒月考)某品牌的手机经过四、五月份连续两次降价,每部售价由2500元降到了1600元,则平均每月降价的百分率是 .
16.(2023八下·锡山期中)如图,在四边形中,,,,E是中点,且,则线段的长度是 .
三、计算题
17.(2024九上·凉州期中)如图,把一块长为,宽为的矩形硬纸板的四角各剪去一个同样大小的正方形,再折叠成一个无盖的长方体纸盒.若该无盖纸盒的底面积为,求剪去的小正方形的边长.
18.(2024九上·即墨月考)[问题提出]:如图1,由n×n×n(长×宽×高)个小立方块组成的正方体中,到底有多少个长方体(包括正方体)呢?
[问题探究]:我们先从较为简单的情形入手.
(1)如图2,由2×1×1个小立方块组成的长方体中,长共有1+2==3条线段,宽和高分别只有1条线段,所以图中共有3×1×1=3个长方体.
(2)如图3,由2×2×1个小立方块组成的长方体中,长和宽分别有1+2==3条线段,高有1条线段,所以图中共有3×3×1=9个长方体.
(3)如图4,由2×2×2个小立方体组成的正方体中,长、宽、高分别有1+2==3条线段,所以图中共有 个长方体.
(4)由2×3×6个小立方块组成的长方体中,长共有1+2==3条线段,宽共有 条线段,高共有 条线段,所以图中共有 个长方体.
[问题解决]
(5)由n×n×n个小立方块组成的正方体中,长、宽、高各有 线段,所以图中共有 个长方体.
[结论应用]
(6)如果由若干个小立方块组成的正方体中共有3375个长方体,那么组成这个正方体的小立方块的个数是多少?请通过计算说明你的结论.
四、解答题
19.(2023九上·甘州月考)某种商品平均每天可销售60件,每件盈利100元.为了尽快减少库存,商场决定采取适当的降价措施,经调查发现,每件商品每降价1元,商场平均每天可多售出2件.据此规律,请回答:
(1)当商场日销售量为80件时,商场日盈利可达到多少元.
(2)为了尽量减少库存,每件商品降价多少元时,商场日盈利可达到8400元?
20.(2024九上·南康期中)某种服装,平均每天可销售件,每件盈利元,若每件降价元,每天可多卖件,如果每天要盈利元,每件应降价多少元?
21.(2023九上·禅城月考)某电子器件厂生产一种电脑显卡,2021年该类电脑显卡的出厂价是200元/个,2022年,2023年连续两年在技术扶贫的帮助下改进技术,降低成本,2023年该电脑显卡的出厂价调整为162元/件.
(1)这两年此类电脑显卡出厂价下降的百分率相同,求平均每年下降的百分率.
(2)2023年某赛格电脑城以出厂价购进若干个此类电脑显卡,以200元/个销售时,平均每天可销售20个.为了尽快减少库存,商场决定降价销售.经调查发现,单价每降低1元,每天可多售出2个,如果每天盈利1150元,单价应降低多少元?
22.(2023九上·青白江期中)如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED边长,易知,这时我们把关于x的形如的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于x的“勾系一元二次方程” 必有实数根;
(3)若x=﹣1是“勾系一元二次方程”的一个根,且四边形ACDE的周长是6,求△ABC面积.
答案解析部分
1.【答案】A
【知识点】一元二次方程的实际应用-销售问题
2.【答案】B
【知识点】一元二次方程的实际应用-销售问题
3.【答案】D
【知识点】一元二次方程的实际应用-百分率问题
4.【答案】B
【知识点】一元二次方程的其他应用
5.【答案】C
【知识点】列一元二次方程
6.【答案】D
【知识点】一元二次方程的应用-几何问题
7.【答案】C
【知识点】一元二次方程的实际应用-百分率问题
8.【答案】A
【知识点】一元二次方程的实际应用-传染问题
9.【答案】B
【知识点】一元二次方程的应用-几何问题
10.【答案】B
【知识点】二次根式的应用;三角形全等及其性质;正方形的性质;一元二次方程的应用-几何问题
11.【答案】
【知识点】一元二次方程的应用-几何问题
12.【答案】x(x-1)=650
【知识点】一元二次方程的应用-几何问题
13.【答案】
【知识点】一元二次方程的实际应用-百分率问题
14.【答案】12
【知识点】一元二次方程的其他应用
15.【答案】20%
【知识点】一元二次方程的实际应用-百分率问题
16.【答案】
【知识点】一元二次方程的其他应用;勾股定理;正方形的判定与性质;三角形全等的判定-SAS
17.【答案】减去的小正方形的边长为
【知识点】一元二次方程的应用-几何问题
18.【答案】(3)27;(4)21,378;(5),;(6)组成这个正方体的小立方块的个数是125个
【知识点】探索图形规律;一元二次方程的应用-几何问题
19.【答案】(1)7200
(2)每件商品降价40元,商场日盈利可8400元;
【知识点】一元二次方程的实际应用-销售问题
20.【答案】每件应降价或元
【知识点】一元二次方程的实际应用-销售问题
21.【答案】(1)解:设平均下降率为,
依题意得:,
解得:,(不合题意,舍去)
答:平均下降率为10%;
(2)解:设单价应降低元,
则每个的销售利润为元,
每天可售出个,
依题意得:,
解得:,,
∵为了减少库存,∴,
答:单价应降低15元
【知识点】一元二次方程的实际应用-百分率问题;一元二次方程的实际应用-销售问题
22.【答案】(1)解:当a=3,b=4,c=5时
勾系一元二次方程为3x2+5x+4=0;
(2)证明:根据题意,得
Δ=(c)2﹣4ab=2c2﹣4ab
∵a2+b2=c2
∴2c2﹣4ab=2(a2+b2)﹣4ab=2(a﹣b)2≥0
即△≥0
∴勾系一元二次方程必有实数根;
(3)解:当x=﹣1时,有a﹣c+b=0,即a+b=c
∵2a+2b+c=6,即2(a+b)+c=6
∴3c=6
∴c=2
∴a2+b2=c2=4,a+b=2
∵(a+b)2=a2+b2+2ab
∴ab=2
∴S△ABC=ab=1.
【知识点】一元二次方程的其他应用
21世纪教育网(www.21cnjy.com)
2 / 8
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
