第三章 概率的进一步认识综合检测题(含答案)
文档属性
| 名称 | 第三章 概率的进一步认识综合检测题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 412.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-09 13:23:25 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第三章 概率的进一步认识
一、单选题(共10题;共30分)
1.(3分)(2024·郸城模拟)一个不透明的口袋中有除标号外完全相同的五个小球,小球上分别标有1,2,3,4,5.随机摸取一个小球然后放回,再随机摸出一个小球.两次取出的小球标号之和为3的倍数的概率是( )
A. B. C. D.
2.(3分)(2023九下·平阳模拟)某日,甲、乙随机乘坐由平阳站开往雁荡山站的直达动车,具体车次如图.各车次各等级座位均有票,则两人乘坐同一趟车的概率是( )
A. B. C. D.
3.(3分)(2020九上·绍兴月考)新冠疫情发生以来,为保证防控期间的口罩供应,某公司加紧转产,开设多条生产线争分夺秒赶制口罩,从最初转产时的陌生,到正式投产后达成日均生产100万个口罩的产能.不仅效率高,而且口罩送检合格率也不断提升,真正体现了“大国速度”.以下是质监局对一批口罩进行质量抽检的相关数据,统计如下:
抽检数量n/个 20 50 100 200 500 1000 2000 5000 10000
合格数量m/个 19 46 93 185 459 922 1840 4595 9213
口罩合格率 0.950 0.920 0.930 0.925 0.918 0.922 0.920 0.919 0.921
下面四个推断合理的是( )
A.当抽检口罩的数量是10000个时,口罩合格的数量是9213个,所以这批口罩中“口罩合格”的概率是0.921;
B.由于抽检口罩的数量分别是50和2000个时,口罩合格率均是0.920,所以可以估计这批口罩中“口罩合格”的概率是0.920;
C.随着抽检数量的增加,“口罩合格”的频率总在0.920附近摆动,显示出一定的稳定性,所以可以估计这批口罩中“口罩合格”的概率是0.920;
D.当抽检口罩的数量达到20000个时,“口罩合格”的概率一定是0.921.
4.(3分)(2022·临沭模拟)小明在一次用频率估计概率的实验中,统计了某一结果出现的频率,并绘制了如图所示的统计图,则符合这一结果的实验可能是( )
A.从一个装有2个白球和1个红球的不透明袋子中任意摸出一球(小球除颜色外,完全相同),摸到红球的概率
B.掷一枚质地均匀的硬币,正面朝上的概率
C.从一副去掉大小王的扑克牌,任意抽取一张,抽到黑桃的概率
D.任意买一张电影票,座位号是2的倍数的概率
5.(3分)(2024九上·期中)在不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次实验发现,摸出红球的频率稳定在0.8左右,则袋子中红球的个数最有可能是( )
A.4个 B.8个 C.12个 D.16个
6.(3分)(2018·河南模拟)九(1)班男生参加体育加试,经抽签分为①②③三个小组,已知小明不在①组,小华不在③组,那么小明与小华分在同一组的概率是( )
A. B. C. D.
7.(3分)将一枚硬币抛掷两次,则这枚硬币两次正面都向上的概率为( )
A. B. C. D.
8.(3分)(2018·凉山)小红上学要经过三个十字路口,每个路口遇到红、绿灯的机会都相同,小红希望上学时经过每个路口都是绿灯,但实际这样的机会是( )
A. B. C. D.
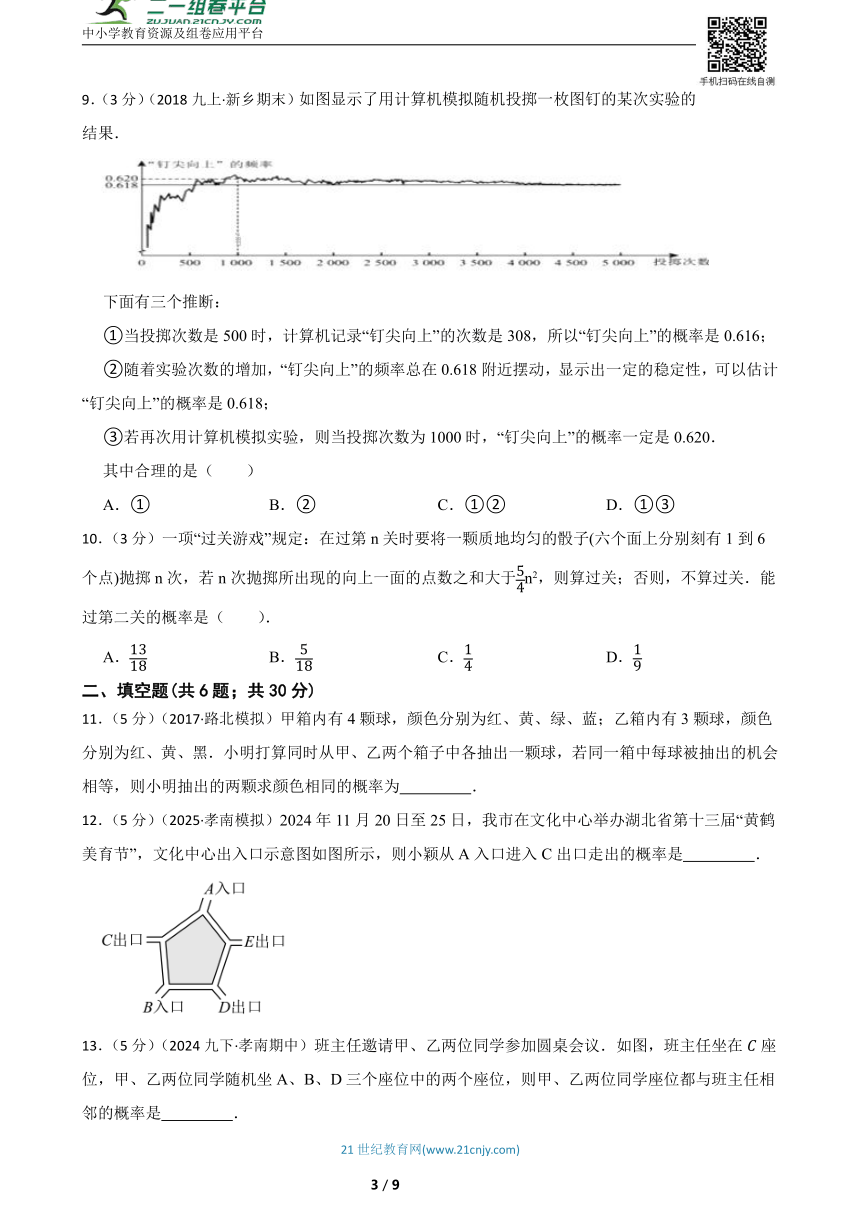
9.(3分)(2018九上·新乡期末)如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.
下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A.① B.② C.①② D.①③
10.(3分)一项“过关游戏”规定:在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6个点)抛掷n次,若n次抛掷所出现的向上一面的点数之和大于n2,则算过关;否则,不算过关.能过第二关的概率是( ).
A. B. C. D.
二、填空题(共6题;共30分)
11.(5分)(2017·路北模拟)甲箱内有4颗球,颜色分别为红、黄、绿、蓝;乙箱内有3颗球,颜色分别为红、黄、黑.小明打算同时从甲、乙两个箱子中各抽出一颗球,若同一箱中每球被抽出的机会相等,则小明抽出的两颗求颜色相同的概率为 .
12.(5分)(2025·孝南模拟)2024年11月20日至25日,我市在文化中心举办湖北省第十三届“黄鹤美育节”,文化中心出入口示意图如图所示,则小颖从A入口进入C出口走出的概率是 .
13.(5分)(2024九下·孝南期中)班主任邀请甲、乙两位同学参加圆桌会议.如图,班主任坐在座位,甲、乙两位同学随机坐A、B、D三个座位中的两个座位,则甲、乙两位同学座位都与班主任相邻的概率是 .
14.(5分)(2024九下·萧山模拟)一个不透明的袋子中装有3个红球和2个白球,这些小球除标号外完全相同,随机摸出两个小球,恰好是一红一白的概率是 .
15.(5分)(2023·新化模拟)如果小球在如图所示的地面上自由滚动,并随机停留在平行四边形内部,那么它最终停留在黑色区域的概率是 .
16.(5分)(2024九上·成都月考)有三张正面分别标有数字,,的不透明卡片,它们除数字不同外其余全部相同现将它们背面朝上,洗匀后从中任意抽取一张,将该卡片正面上的数字记为;不放回,再从中任意抽取一张,将该卡片正面朝上的数字记为,则使关于的不等式组的解集中有且只有个非负整数的概率为 .
三、计算题(共2题;共19分)
17.(12分)(2023七下·金凤期末)小明和小亮两位同学做掷骰子(质地均匀的正方体)游戏,他们共做了100次试验,结果如下:
朝上的点数 1 2 3 4 5 6
出现的次数 16 14 25 20 12 13
(1)(4分)计算“点数1朝上”的频率和“点数6朝上”的频率;
(2)(4分)小亮说:“若投掷1000次,则出现点数4朝上的次数正好是200次”,小亮的说法_________(填“正确”或“不正确”);
(3)(4分)小明将一枚骰子任意投掷一次,求朝上的点数不小于4的概率.
18.(7分)(2025八下·东台月考)某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据:
(1)计算并完成表格:
转动转盘的次数n 100 150 200 500 800 1000
落在“铅笔”的次数m 68 111 136 345 564 701
落在“铅笔”的频率m/n 0.68 0.74 △ 0.69 0.705 △
(2)请估计,当n很大时,频率将会接近多少
(3)假如你去转动该转盘一次,你获得铅笔的概率约是多少
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少 (精确到1°)
四、解答题(共4题;共41分)
19.(9分)(2024·福州模拟)九年级数学课外小组在开展活动时,设计了这样一个数学活动.有A、B两组卡片,每组各3张,A组卡片上分别写有1,3,5;B组卡片上分别写有,,.每张卡片除正面写有不同数字外,其余均相同.甲从A组中随机抽取一张记为x,乙从B组中随机抽取一张记为y.
(1)(4分)若甲抽出的数字是1,乙抽出的数是,它们恰好是的解,求m的值;
(2)(5分)在(1)的条件下,求甲、乙随机抽取一次的数恰好是方程的解的概率.(请用树状图或列表法求解)
20.(9分)(2023九上·宿迁月考)把算珠放在计数器的3根插棒上可以构成一个数,例如:如图摆放的算珠表示数.
(1)(4分)若将一颗算珠任意摆放在这3根插棒上,则构成的数是三位数的概率是______________;
(2)(5分)现将两颗算珠任意摆放在这3根插棒上,先放一颗算珠,再放另一颗,请用列表或画树状图的方法,求构成的数是两位数的概率.
21.(9分)(2022九下·衡阳模拟)为进一步巩固“青年大学习”网上主题团课学习成果,某校计划开展团课学习知识竞赛活动.竞赛试题共有A、B、C三组,小云和小敏两位同学都将参加本次团课学习知识竞赛.
(1)(4分)小云抽中B组试题的概率是 ;
(2)(5分)利用画树状图或列表的方法,求小云和小敏抽到的是同一组试题的概率.
22.(14分)模拟经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种情况是等可能的,当同向行驶的三辆汽车经过这个十字路口时,
(1)(4分)求三辆车全部同向而行的概率.
(2)(5分)求至少有两辆车向左转的概率.
(3)(5分)这个路口汽车左转.右转、直行的指示绿灯交替亮起,亮的时间均为30秒.交管部门对这个十字路口交通高峰时段车流量作了统计,发现汽车在此十字路口向右转的频率为,向左转和直行的频率均为,在绿灯亮的总时间不变的条件下,为使交通更加通畅,请你用统计的知识对此十字路口三个方向的绿灯亮的时间做出合理的调整.
答案解析部分
1.【答案】D
【知识点】用列表法或树状图法求概率
2.【答案】B
【知识点】用列表法或树状图法求概率
3.【答案】C
【知识点】利用频率估计概率;概率的简单应用
4.【答案】A
【知识点】利用频率估计概率
5.【答案】D
【知识点】利用频率估计概率;简单事件概率的计算
6.【答案】C
【知识点】用列表法或树状图法求概率;概率公式
7.【答案】C
【知识点】几何概率
8.【答案】B
【知识点】用列表法或树状图法求概率;概率公式
9.【答案】B
【知识点】利用频率估计概率
10.【答案】A
【知识点】用列表法或树状图法求概率;概率公式
11.【答案】
【知识点】用列表法或树状图法求概率
12.【答案】
【知识点】用列表法或树状图法求概率;概率公式
13.【答案】
【知识点】用列表法或树状图法求概率
14.【答案】
【知识点】用列表法或树状图法求概率;概率公式
15.【答案】
【知识点】几何概率
16.【答案】
【知识点】解一元一次不等式组;一元一次不等式组的特殊解;几何概率;用列表法或树状图法求概率
17.【答案】(1)“点数1朝上”的频率0.16;“点数6朝上”的频率0.13
(2)不正确
(3)
【知识点】频数与频率;利用频率估计概率;概率公式
18.【答案】(1)0.68 , 0.701 ;(2)0.7;(3)0.7;(4)252°.
【知识点】利用频率估计概率
19.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
20.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
21.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
22.【答案】(1)解:分别用A、B、C表示向左转,直行,向右转,根据题意画出树状图如下:
由图可知:共有27种等可能的结果数,三辆车全部同向而行的有3种情况,
∴P( 三辆车全部同向而行的概率)= ;
(2)解:∵至少有两辆车向左转的情况数有7种,
∴P( 至少有两辆车向左转 )=;
(3)解:∵汽车向右转、向左转,直行的概率分别为,
∴ 在绿灯亮的总时间不变的条件下可以调整绿灯亮的时间如下:
向左转及直行的绿灯亮的时间都为:(秒),
向右转绿灯亮的时间为:(秒).
【知识点】用列表法或树状图法求概率;概率的简单应用
21世纪教育网(www.21cnjy.com)
2 / 9
第三章 概率的进一步认识
一、单选题(共10题;共30分)
1.(3分)(2024·郸城模拟)一个不透明的口袋中有除标号外完全相同的五个小球,小球上分别标有1,2,3,4,5.随机摸取一个小球然后放回,再随机摸出一个小球.两次取出的小球标号之和为3的倍数的概率是( )
A. B. C. D.
2.(3分)(2023九下·平阳模拟)某日,甲、乙随机乘坐由平阳站开往雁荡山站的直达动车,具体车次如图.各车次各等级座位均有票,则两人乘坐同一趟车的概率是( )
A. B. C. D.
3.(3分)(2020九上·绍兴月考)新冠疫情发生以来,为保证防控期间的口罩供应,某公司加紧转产,开设多条生产线争分夺秒赶制口罩,从最初转产时的陌生,到正式投产后达成日均生产100万个口罩的产能.不仅效率高,而且口罩送检合格率也不断提升,真正体现了“大国速度”.以下是质监局对一批口罩进行质量抽检的相关数据,统计如下:
抽检数量n/个 20 50 100 200 500 1000 2000 5000 10000
合格数量m/个 19 46 93 185 459 922 1840 4595 9213
口罩合格率 0.950 0.920 0.930 0.925 0.918 0.922 0.920 0.919 0.921
下面四个推断合理的是( )
A.当抽检口罩的数量是10000个时,口罩合格的数量是9213个,所以这批口罩中“口罩合格”的概率是0.921;
B.由于抽检口罩的数量分别是50和2000个时,口罩合格率均是0.920,所以可以估计这批口罩中“口罩合格”的概率是0.920;
C.随着抽检数量的增加,“口罩合格”的频率总在0.920附近摆动,显示出一定的稳定性,所以可以估计这批口罩中“口罩合格”的概率是0.920;
D.当抽检口罩的数量达到20000个时,“口罩合格”的概率一定是0.921.
4.(3分)(2022·临沭模拟)小明在一次用频率估计概率的实验中,统计了某一结果出现的频率,并绘制了如图所示的统计图,则符合这一结果的实验可能是( )
A.从一个装有2个白球和1个红球的不透明袋子中任意摸出一球(小球除颜色外,完全相同),摸到红球的概率
B.掷一枚质地均匀的硬币,正面朝上的概率
C.从一副去掉大小王的扑克牌,任意抽取一张,抽到黑桃的概率
D.任意买一张电影票,座位号是2的倍数的概率
5.(3分)(2024九上·期中)在不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次实验发现,摸出红球的频率稳定在0.8左右,则袋子中红球的个数最有可能是( )
A.4个 B.8个 C.12个 D.16个
6.(3分)(2018·河南模拟)九(1)班男生参加体育加试,经抽签分为①②③三个小组,已知小明不在①组,小华不在③组,那么小明与小华分在同一组的概率是( )
A. B. C. D.
7.(3分)将一枚硬币抛掷两次,则这枚硬币两次正面都向上的概率为( )
A. B. C. D.
8.(3分)(2018·凉山)小红上学要经过三个十字路口,每个路口遇到红、绿灯的机会都相同,小红希望上学时经过每个路口都是绿灯,但实际这样的机会是( )
A. B. C. D.
9.(3分)(2018九上·新乡期末)如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.
下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A.① B.② C.①② D.①③
10.(3分)一项“过关游戏”规定:在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6个点)抛掷n次,若n次抛掷所出现的向上一面的点数之和大于n2,则算过关;否则,不算过关.能过第二关的概率是( ).
A. B. C. D.
二、填空题(共6题;共30分)
11.(5分)(2017·路北模拟)甲箱内有4颗球,颜色分别为红、黄、绿、蓝;乙箱内有3颗球,颜色分别为红、黄、黑.小明打算同时从甲、乙两个箱子中各抽出一颗球,若同一箱中每球被抽出的机会相等,则小明抽出的两颗求颜色相同的概率为 .
12.(5分)(2025·孝南模拟)2024年11月20日至25日,我市在文化中心举办湖北省第十三届“黄鹤美育节”,文化中心出入口示意图如图所示,则小颖从A入口进入C出口走出的概率是 .
13.(5分)(2024九下·孝南期中)班主任邀请甲、乙两位同学参加圆桌会议.如图,班主任坐在座位,甲、乙两位同学随机坐A、B、D三个座位中的两个座位,则甲、乙两位同学座位都与班主任相邻的概率是 .
14.(5分)(2024九下·萧山模拟)一个不透明的袋子中装有3个红球和2个白球,这些小球除标号外完全相同,随机摸出两个小球,恰好是一红一白的概率是 .
15.(5分)(2023·新化模拟)如果小球在如图所示的地面上自由滚动,并随机停留在平行四边形内部,那么它最终停留在黑色区域的概率是 .
16.(5分)(2024九上·成都月考)有三张正面分别标有数字,,的不透明卡片,它们除数字不同外其余全部相同现将它们背面朝上,洗匀后从中任意抽取一张,将该卡片正面上的数字记为;不放回,再从中任意抽取一张,将该卡片正面朝上的数字记为,则使关于的不等式组的解集中有且只有个非负整数的概率为 .
三、计算题(共2题;共19分)
17.(12分)(2023七下·金凤期末)小明和小亮两位同学做掷骰子(质地均匀的正方体)游戏,他们共做了100次试验,结果如下:
朝上的点数 1 2 3 4 5 6
出现的次数 16 14 25 20 12 13
(1)(4分)计算“点数1朝上”的频率和“点数6朝上”的频率;
(2)(4分)小亮说:“若投掷1000次,则出现点数4朝上的次数正好是200次”,小亮的说法_________(填“正确”或“不正确”);
(3)(4分)小明将一枚骰子任意投掷一次,求朝上的点数不小于4的概率.
18.(7分)(2025八下·东台月考)某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据:
(1)计算并完成表格:
转动转盘的次数n 100 150 200 500 800 1000
落在“铅笔”的次数m 68 111 136 345 564 701
落在“铅笔”的频率m/n 0.68 0.74 △ 0.69 0.705 △
(2)请估计,当n很大时,频率将会接近多少
(3)假如你去转动该转盘一次,你获得铅笔的概率约是多少
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少 (精确到1°)
四、解答题(共4题;共41分)
19.(9分)(2024·福州模拟)九年级数学课外小组在开展活动时,设计了这样一个数学活动.有A、B两组卡片,每组各3张,A组卡片上分别写有1,3,5;B组卡片上分别写有,,.每张卡片除正面写有不同数字外,其余均相同.甲从A组中随机抽取一张记为x,乙从B组中随机抽取一张记为y.
(1)(4分)若甲抽出的数字是1,乙抽出的数是,它们恰好是的解,求m的值;
(2)(5分)在(1)的条件下,求甲、乙随机抽取一次的数恰好是方程的解的概率.(请用树状图或列表法求解)
20.(9分)(2023九上·宿迁月考)把算珠放在计数器的3根插棒上可以构成一个数,例如:如图摆放的算珠表示数.
(1)(4分)若将一颗算珠任意摆放在这3根插棒上,则构成的数是三位数的概率是______________;
(2)(5分)现将两颗算珠任意摆放在这3根插棒上,先放一颗算珠,再放另一颗,请用列表或画树状图的方法,求构成的数是两位数的概率.
21.(9分)(2022九下·衡阳模拟)为进一步巩固“青年大学习”网上主题团课学习成果,某校计划开展团课学习知识竞赛活动.竞赛试题共有A、B、C三组,小云和小敏两位同学都将参加本次团课学习知识竞赛.
(1)(4分)小云抽中B组试题的概率是 ;
(2)(5分)利用画树状图或列表的方法,求小云和小敏抽到的是同一组试题的概率.
22.(14分)模拟经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种情况是等可能的,当同向行驶的三辆汽车经过这个十字路口时,
(1)(4分)求三辆车全部同向而行的概率.
(2)(5分)求至少有两辆车向左转的概率.
(3)(5分)这个路口汽车左转.右转、直行的指示绿灯交替亮起,亮的时间均为30秒.交管部门对这个十字路口交通高峰时段车流量作了统计,发现汽车在此十字路口向右转的频率为,向左转和直行的频率均为,在绿灯亮的总时间不变的条件下,为使交通更加通畅,请你用统计的知识对此十字路口三个方向的绿灯亮的时间做出合理的调整.
答案解析部分
1.【答案】D
【知识点】用列表法或树状图法求概率
2.【答案】B
【知识点】用列表法或树状图法求概率
3.【答案】C
【知识点】利用频率估计概率;概率的简单应用
4.【答案】A
【知识点】利用频率估计概率
5.【答案】D
【知识点】利用频率估计概率;简单事件概率的计算
6.【答案】C
【知识点】用列表法或树状图法求概率;概率公式
7.【答案】C
【知识点】几何概率
8.【答案】B
【知识点】用列表法或树状图法求概率;概率公式
9.【答案】B
【知识点】利用频率估计概率
10.【答案】A
【知识点】用列表法或树状图法求概率;概率公式
11.【答案】
【知识点】用列表法或树状图法求概率
12.【答案】
【知识点】用列表法或树状图法求概率;概率公式
13.【答案】
【知识点】用列表法或树状图法求概率
14.【答案】
【知识点】用列表法或树状图法求概率;概率公式
15.【答案】
【知识点】几何概率
16.【答案】
【知识点】解一元一次不等式组;一元一次不等式组的特殊解;几何概率;用列表法或树状图法求概率
17.【答案】(1)“点数1朝上”的频率0.16;“点数6朝上”的频率0.13
(2)不正确
(3)
【知识点】频数与频率;利用频率估计概率;概率公式
18.【答案】(1)0.68 , 0.701 ;(2)0.7;(3)0.7;(4)252°.
【知识点】利用频率估计概率
19.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
20.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
21.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
22.【答案】(1)解:分别用A、B、C表示向左转,直行,向右转,根据题意画出树状图如下:
由图可知:共有27种等可能的结果数,三辆车全部同向而行的有3种情况,
∴P( 三辆车全部同向而行的概率)= ;
(2)解:∵至少有两辆车向左转的情况数有7种,
∴P( 至少有两辆车向左转 )=;
(3)解:∵汽车向右转、向左转,直行的概率分别为,
∴ 在绿灯亮的总时间不变的条件下可以调整绿灯亮的时间如下:
向左转及直行的绿灯亮的时间都为:(秒),
向右转绿灯亮的时间为:(秒).
【知识点】用列表法或树状图法求概率;概率的简单应用
21世纪教育网(www.21cnjy.com)
2 / 9
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
