【期末押题卷】浙江省杭州市2025-2026学年五年级上学期期末模拟数学预测卷人教版(含解析)
文档属性
| 名称 | 【期末押题卷】浙江省杭州市2025-2026学年五年级上学期期末模拟数学预测卷人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 673.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 21:59:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙江省杭州市2025-2026学年五年级上学期期末模拟数学预测卷
一.填空题(共9小题,满分18分,每小题2分)
1.(2分)根据算式23×16=368,直接写出得数。
0.23×1.6= 230×0.16= 0.23×0.16=
2.(2分)
(1)一包饼干和一袋瓜子一共多少元?
(2)一袋果冻比一盒薯片贵多少元?
(3)奇思想买一袋面包和一袋果冻,他只有8元,够吗?
(4)妙想有5元,可以买哪两种食物?请给出两种买法。
第一种食物价钱 第二种食物价钱 合计钱数 剩余钱数
买法一
买法二
3.(2分)甲数是乙数的13倍,甲数除以乙数的商是 ;如果甲数扩大到原来的8倍,要使商不变,乙数应 。
4.(2分)在横线里填上“>”“<”或“=”。
0.84÷1.5 0.84
2.12÷0.4 2.12×0.4
5.(2分)一根彩带长19.2米,把它对折三次,平均每段长 分米。
6.(2分)一桶乒乓球有a个。
3元/个 2.7g/个
(1)体育老师又买来了3个,现在有 个乒乓球;
(2)塑料桶重100g,原来这一桶乒乓球连瓶共重 g;
(3)如果这一桶乒乓球连瓶共重154g,买来的时候是整桶购买的,花费50元,那么每个便宜了
元。
7.(2分)根据规律写出答案。
1×1=1
11×11=121
111×111=12321
1111×1111=1234321
11111×11111=
8.(2分)如图,在一个梯形中剪去一个最大的平行四边形,这个平行四边形的面积是 平方厘米,剩下的图形的面积是 平方厘米。
9.(2分)在框里填上合适的数。
二.选择题(共6小题,满分12分,每小题2分)
10.(2分)下列方程中,与1.8x﹣1.2=2.4的解不相等的是( )
A.1.8x=2.4+1.2 B.1.8x﹣2.4=1.2
C.1.8x=2.4﹣1.2 D.18x﹣12=24
11.(2分)两个因数都是0.9,写成算式是( )
A.0.9×2 B.0.9×0.9 C.0.9+0.9 D.0.9﹣0.9
12.(2分)如图中,两个正方形的边长都是5分米,阴影部分的面积是( )
A.10dm2 B.15dm2 C.20dm2 D.25dm2
13.(2分)如图中每个小方格表示边长为1厘米的正方形,曲线所围成图形的面积大约是( )厘米2。
A.70 B.50 C.40 D.30
14.(2分)从一副扑克牌中任意抽出一张,那么抽出的一张中,( )
A.大王或小王的可能性最小。
B.是梅花或方块的可能性大些。
C.红桃或黑桃的可能性大些。
15.(2分)一台学习机原价是701元,现价是598元,大约便宜了( )元。
A.100 B.103 C.200
三.计算题(共4小题,满分30分)
16.(8分)直接写得数。
5.6÷7= 39×0.2= 1÷0.25= 2.4×500=
2÷0.01= 10﹣5.91= a+0.8a= 0.92=
7.85×0.9×0= 0.5×4÷0.5×4=
17.(8分)列竖式计算。
2.9×0.56≈(得数保留一位小数)
5.7÷9=(得数用循环小数表示)
18.(8分)脱式计算。
80×0.25×0.4×12.5 7.22×8.4+8.4×2.78
1.7÷0.25÷0.4 6.5+3.5÷0.05
19.(6分)解方程。
2x+120=200 x﹣54.21=69 x+2.5=3.8
四.选择题(共7小题,满分14分,每小题2分)
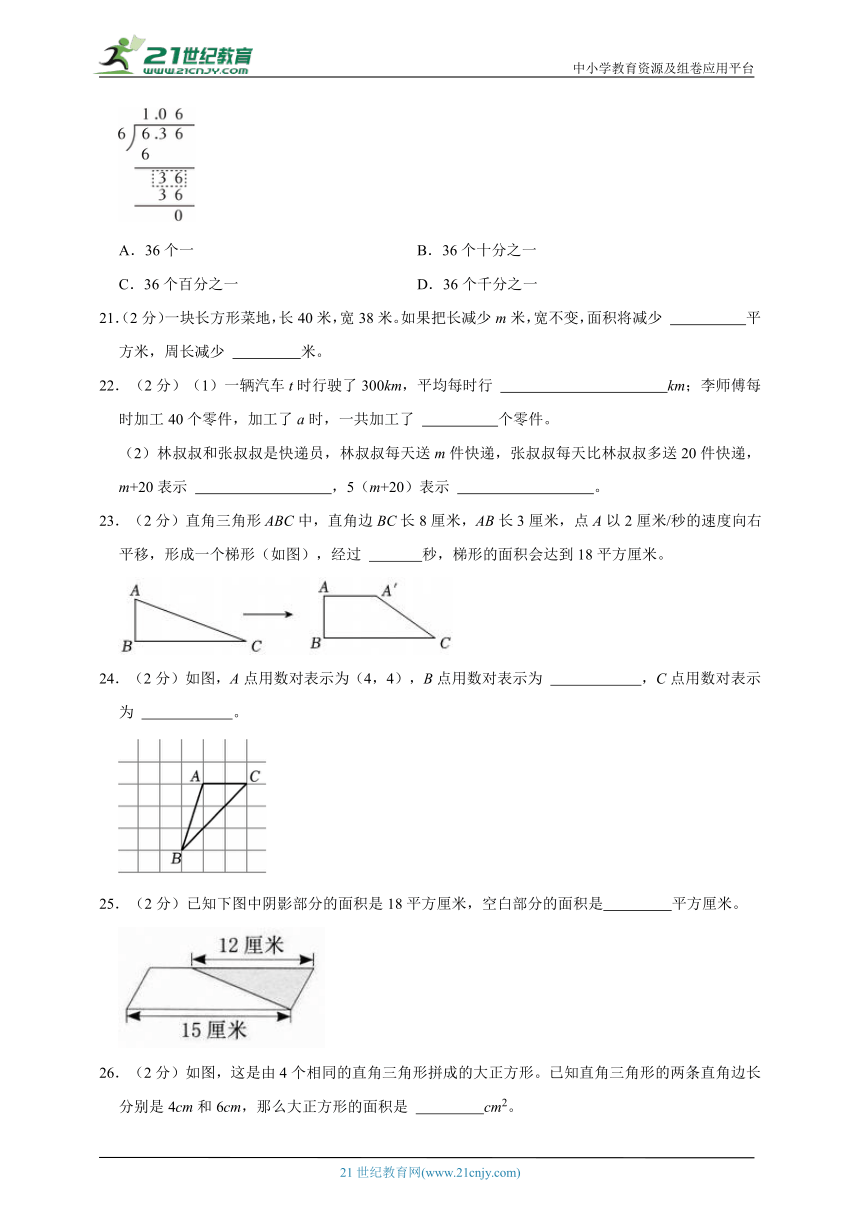
20.(2分)如图竖式虚线框中的部分表示( )
A.36个一 B.36个十分之一
C.36个百分之一 D.36个千分之一
21.(2分)一块长方形菜地,长40米,宽38米。如果把长减少m米,宽不变,面积将减少 平方米,周长减少 米。
22.(2分)(1)一辆汽车t时行驶了300km,平均每时行 km;李师傅每时加工40个零件,加工了a时,一共加工了 个零件。
(2)林叔叔和张叔叔是快递员,林叔叔每天送m件快递,张叔叔每天比林叔叔多送20件快递,m+20表示 ,5(m+20)表示 。
23.(2分)直角三角形ABC中,直角边BC长8厘米,AB长3厘米,点A以2厘米/秒的速度向右平移,形成一个梯形(如图),经过 秒,梯形的面积会达到18平方厘米。
24.(2分)如图,A点用数对表示为(4,4),B点用数对表示为 ,C点用数对表示为 。
25.(2分)已知下图中阴影部分的面积是18平方厘米,空白部分的面积是 平方厘米。
26.(2分)如图,这是由4个相同的直角三角形拼成的大正方形。已知直角三角形的两条直角边长分别是4cm和6cm,那么大正方形的面积是 cm2。
五.应用题(共6小题,满分26分)
27.(4分)张叔叔乘坐汕头出租车行驶了8.4km,使用手机付款,且有一个可用的3.05元的“红包”,张叔叔实际支付多少元?
里程 收费标准
3km及以内 9元
超过3km的部分 每千米2.4元 (不足1km,按1km计算)
28.(4分)小华在帮妈妈核实消费账单时,把账单上的5.3元看成了5.8元,结果得到的总金额为10元,与账单对不上,正确的结果是多少呢?
29.(6分)圆形湖的周长是1350米,沿湖边每隔9米种一棵柳树,在两棵柳树之间等距离种桃树2棵。一共种了多少棵桃树?
30.(4分)重庆居民生活用电规定:每月不超过200千瓦时(含200千瓦时),按每千瓦时0.52元收取电费;超过200千瓦时的部分按每千瓦时0.57元收取电费。若8月份文乐家共花费149.6元电费,则文乐家8月份用电多少千瓦时?
31.(4分)佳佳挑出了26块饼干,打算把它们装袋送给朋友们品尝。有两种包装袋,一种是塑料袋,每袋装5块,另一种是纸袋,每袋装3块。如果每袋都装满,怎样装能恰好装完?把装饼干的方案填写在如表中并答题。
方案序号 塑料袋(每袋装5块) 纸袋(每袋装3块) 饼干块数
① 6袋 0袋 5×6=30(块)
② 5袋 1袋 5×5+3×1=28(块)
③
④
⑤
⑥
⑦
32.(4分)一块菜地的形状如图(阴影部分),图中每个小方格的边长为1m,那么这块菜地的面积是多少平方米?
浙江省杭州市2025-2026学年五年级上学期期末模拟数学预测卷
参考答案与试题解析
一.填空题(共9小题,满分18分,每小题2分)
1.(2分)根据算式23×16=368,直接写出得数。
0.23×1.6= 0.368 230×0.16= 36.8 0.23×0.16= 0.0368
【考点】积的变化规律.
【专题】运算能力.
【答案】0.368,36.8,0.0368。
【分析】根据积的变化规律:两数相乘,如果一个因数乘(或除以)几(0除外),另一个因数也乘(或除以)几(0除外),原来的积就乘(或除以)它们的乘积。
【解答】解:根据算式23×16=368,可得:
0.23×1.6=0.368 230×0.16=36.8 0.23×0.16=0.0368
故答案为:0.368,36.8,0.0368。
【点评】本题考查的是积的变化规律,准确判断因数发生的变化是解决本题的关键。
2.(2分)
(1)一包饼干和一袋瓜子一共多少元?
(2)一袋果冻比一盒薯片贵多少元?
(3)奇思想买一袋面包和一袋果冻,他只有8元,够吗?
(4)妙想有5元,可以买哪两种食物?请给出两种买法。
第一种食物价钱 第二种食物价钱 合计钱数 剩余钱数
买法一
1.20
2.50
3.70
1.30
买法二
2.50
0.80
3.30
1.70
【考点】整数、小数复合应用题.
【专题】综合题;应用意识.
【答案】(1)6.30元;
(2)2.10元;
(3)不够;
(4)
第一种食物价钱 第二种食物价钱 合计钱数 剩余钱数
买法一 1.20 2.50 3.70 1.30
买法二 2.50 0.80 3.30 1.70
(答案不唯一)
【分析】(1)用加法列式计算一包饼干和一袋瓜子一共多少元;
(2)用减法列式计算一袋果冻比一盒薯片贵多少元;
(3)用加法列式计算买一袋面包和一袋果冻的价钱,然后和8元比较大小;
(4)两种食物的价钱不超过5元就符合要求,由此解答本题(答案不唯一)。
【解答】解:(1)3.80+2.50=6.30(元)
答:一包饼干和一袋瓜子一共6.30元。
(2)6.50﹣4.40=2.10(元)
答:一袋果冻比一盒薯片贵2.10元。
(3)1.80+6.50=8.30(元)
8.30>8
答:奇思想买一袋面包和一袋果冻,8元不够。
(4)1.20+2.50=3.70(元)
5﹣3.70=1.30(元)
2.50+0.80=3.30(元)
5﹣3.30=1.70(元)
第一种食物价钱 第二种食物价钱 合计钱数 剩余钱数
买法一 1.20 2.50 3.70 1.30
买法二 2.50 0.80 3.30 1.70
(答案不唯一)
【点评】解决本题的关键是找出题中的数量关系,利用数量关系列式计算。
3.(2分)甲数是乙数的13倍,甲数除以乙数的商是 13 ;如果甲数扩大到原来的8倍,要使商不变,乙数应 扩大到原来的8倍 。
【考点】商的变化规律.
【专题】运算能力.
【答案】13,扩大到原来的8倍。
【分析】在除法算式中,被除数和除数同时扩大或缩小相同的倍数(0除外),商不变;据此解答即可。
【解答】解:甲数是乙数的13倍,甲数除以乙数的商是13。
根据商不变的性质可知,如果甲数扩大到原来的8倍,要使商不变,乙数应扩大到原来的8倍。
故答案为:13,扩大到原来的8倍。
【点评】解答此题应明确:只有被除数和除数同时扩大或缩小相同的倍数(0除外),商才不变。
4.(2分)在横线里填上“>”“<”或“=”。
0.84÷1.5 < 0.84
2.12÷0.4 > 2.12×0.4
【考点】商的变化规律;积的变化规律.
【专题】数据分析观念.
【答案】<,>。
【分析】一个数(0除外)除以一个大于1的数,商小于原数;一个数(0除外)除以一个小于1的数,商大于原数;一个数(0除外)乘一个小于1的数,积小于原数。据此解答。
【解答】解:0.84÷1.5<0.84
2.12÷0.4>2.12×0.4
故答案为:<,>。
【点评】熟练掌握商的变化规律和积的变化规律是解题的关键。
5.(2分)一根彩带长19.2米,把它对折三次,平均每段长 24 分米。
【考点】小数除法.
【专题】综合填空题;应用意识.
【答案】24。
【分析】对折三次,则这根彩带被平均分成8段,用除法列式计算平均每段长多少分米。
【解答】解:19.2米=192分米,对折三次,则这根彩带被平均分成8段,每段长度:192÷8=24(分米)
故答案为:24。
【点评】解决本题的关键是找出题中数量关系。
6.(2分)一桶乒乓球有a个。
3元/个 2.7g/个
(1)体育老师又买来了3个,现在有 (a+3) 个乒乓球;
(2)塑料桶重100g,原来这一桶乒乓球连瓶共重 (100+2.7a) g;
(3)如果这一桶乒乓球连瓶共重154g,买来的时候是整桶购买的,花费50元,那么每个便宜了 (3﹣50÷a) 元。
【考点】用字母表示数;整数、小数复合应用题.
【专题】运算能力;应用意识.
【答案】(1)(a+3);(2)(100+2.7a);(3)(3﹣50÷a)。
【分析】(1)现在有乒乓球的个数=原来一桶乒乓球的个数+体育老师又买来的个数;
(2)原来这一桶乒乓球连瓶一共的质量=塑料桶的质量+平均每个乒乓的质量×原来的个数;
(3)每个便宜的钱数=零售价﹣整桶买的单价;其中,整桶买的单价=总价÷整桶的个数。
【解答】解:(1)(a+3)个
体育老师又买来了3个,现在有(a+3)个乒乓球。
(2)100+2.7×a=(100+2.7a)g
塑料桶重100g,原来这一桶乒乓球连瓶共重(100+2.7)g。
(3)(3﹣50÷a)元
如果这一桶乒乓球连瓶共重154g,买来的时候是整桶购买的,花费50元,那么每个便宜了(3﹣50÷a)元。
故答案为:(a+3);(100+2.7a);(3﹣50÷a)。
【点评】本题考查用字母表示数,关键是弄清楚它们之间的关系。
7.(2分)根据规律写出答案。
1×1=1
11×11=121
111×111=12321
1111×1111=1234321
11111×11111= 123454321
【考点】“式”的规律.
【专题】规律型;探索数的规律;运算能力.
【答案】123454321。
【分析】1×1=1
11×11=121
111×111=12321
1111×1111=1234321
因数各个位上的数字都是1,当因数是n位数时,积各个位上数字是由1排到n,再由n排到1,即:123……n……321;据此解答即可。
【解答】解:1×1=1
11×11=121
111×111=12321
1111×1111=1234321
11111×11111=123454321
故答案为:123454321。
【点评】主要考查了“式”的规律,同时考查了学生的分析、总结、归纳能力,规律型的习题一般是从所给的数据和运算方法进行分析,从特殊值的规律上总结出一般性的规律。
8.(2分)如图,在一个梯形中剪去一个最大的平行四边形,这个平行四边形的面积是 120 平方厘米,剩下的图形的面积是 60 平方厘米。
【考点】平行四边形的面积;梯形的面积.
【专题】应用题;应用意识.
【答案】120;60。
【分析】由图可知,一个梯形的上底长12厘米,下底长24厘米,高10厘米,若在这个梯形中剪去一个最大的平行四边形,这个平行四边形的底是12厘米,高是10厘米;
剩余部分是一个三角形,这个三角形的底是(24﹣12)厘米,高是10厘米;
根据平行四边形的面积=底×高,三角形的面积=底×高÷2,解答此题即可。
【解答】解:12×10=120(平方厘米)
(24﹣12)×10÷2
=12×10÷2
=120÷2
=60(平方厘米)
答:这个平行四边形的面积是 120平方厘米,剩下的图形的面积是 60平方厘米。
故答案为:120;60。
【点评】熟练掌握平行四边形和三角形的面积公式,是解答此题的关键。
9.(2分)在框里填上合适的数。
【考点】竖式数字谜.
【专题】计算题;运算能力.
【答案】
【分析】第一题,积是469,第一个因数的个位数字是7,7×7=49,所以第二个因数是7,用469÷7得出第一个因数。
第二题,2+7=9,得出被减数是929,然后根据929减482算出减数。
【解答】解:如下所示:
【点评】解答本题的关键是熟练掌握竖式乘法和竖式加法的计算方法,正确找出从哪个数位入手。
二.选择题(共6小题,满分12分,每小题2分)
10.(2分)下列方程中,与1.8x﹣1.2=2.4的解不相等的是( )
A.1.8x=2.4+1.2 B.1.8x﹣2.4=1.2
C.1.8x=2.4﹣1.2 D.18x﹣12=24
【考点】小数方程求解.
【专题】应用题;应用意识.
【答案】C
【分析】根据等式的基本性质,分别求出每个方程的解,然后解答即可。
【解答】解:1.8x﹣1.2=2.4
1.8x=2.4+1.2
1.8x=3.6
x=3.6÷1.8
x=2
1.8x=2.4+1.2
1.8x=3.6
x=3.6÷1.8
x=2
1.8x﹣2.4=1.2
1.8x=2.4+1.2
1.8x=3.6
x=3.6÷1.8
x=2
1.8x=2.4﹣1.2
1.8x=1.2
x=1.2÷1.8
x
18x﹣12=24
18x=12+24
18x=36
x=36÷18
x=2
故选:C。
【点评】解答此题要运用等式的基本性质。
11.(2分)两个因数都是0.9,写成算式是( )
A.0.9×2 B.0.9×0.9 C.0.9+0.9 D.0.9﹣0.9
【考点】小数乘法.
【专题】综合判断题;运算能力.
【答案】B
【分析】根据题意,两个因数都是0.9,可知,一个因数是0.9,另一个因数也是0.9,再根据小数乘法进行列式即可。
【解答】解:根据题意可得:一个因数是0.9,另一个因数也是0.9,所以,算式是:0.9×0.9。
故选:B。
【点评】根据乘法各部分的名称进行解答即可。
12.(2分)如图中,两个正方形的边长都是5分米,阴影部分的面积是( )
A.10dm2 B.15dm2 C.20dm2 D.25dm2
【考点】组合图形的面积.
【专题】几何直观;推理能力;应用意识.
【答案】D
【分析】通过观察图形可知,阴影部分的面积通过平移“转化”为一个正方形的面积,根据正方形的面积=边长×边长,把数据代入公式解答。
【解答】解:5×5=25(平方分米)
答:阴影部分的面积是25平方分米。
故选:D。
【点评】此题主要考查正方形面积公式的灵活运用,关键是通过平移把阴影部分的面积转化我应该正方形的面积。
13.(2分)如图中每个小方格表示边长为1厘米的正方形,曲线所围成图形的面积大约是( )厘米2。
A.70 B.50 C.40 D.30
【考点】用方格纸计算图形面积.
【专题】几何直观.
【答案】B
【分析】根据图示,图中曲线所围成图形近似一个长10厘米,宽5厘米的长方形,根据长方形的面积公式解答即可。
【解答】解:10×5=50(平方厘米)
答:曲线所围成图形的面积大约是50厘米。
故选:B。
【点评】本题考查了面积估算知识,结合题意分析解答即可。
14.(2分)从一副扑克牌中任意抽出一张,那么抽出的一张中,( )
A.大王或小王的可能性最小。
B.是梅花或方块的可能性大些。
C.红桃或黑桃的可能性大些。
【考点】可能性的大小.
【专题】可能性;应用意识.
【答案】A
【分析】根据不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。据此解答即可。
【解答】解:一副扑克牌中,大王和小王各有一张,梅花、方块、红桃、黑桃各有13张;
所以抽出的一张中,梅花、方块、红桃、黑桃的可能性一样,大王或小王的可能性最小。
故选:A。
【点评】解答此题的关键:应明确可能性的计算方法,并能根据实际情况进行灵活运用。
15.(2分)一台学习机原价是701元,现价是598元,大约便宜了( )元。
A.100 B.103 C.200
【考点】数的估算.
【专题】运算能力;应用意识.
【答案】A
【分析】用学习机原件减去现价,把701看作700,598看作600进行估算即可。
【解答】解:701﹣598
≈700﹣600
=100(元)
答:大约便宜了100元。
故选:A。
【点评】本题考查了数的估算,可以把数看作近似整十、整百、整千……的数进行估算。
三.计算题(共4小题,满分30分)
16.(8分)直接写得数。
5.6÷7= 39×0.2= 1÷0.25= 2.4×500=
2÷0.01= 10﹣5.91= a+0.8a= 0.92=
7.85×0.9×0= 0.5×4÷0.5×4=
【考点】小数除法;有理数的乘方;小数乘法.
【专题】运算能力.
【答案】0.8;7.8;4;1200,200;4.09;1.8a;0.81,0;16。
【分析】运用小数的乘除法的计算法则进行计算即可。
【解答】解:
5.6÷7=0.8 39×0.2=7.8 1÷0.25=4 2.4×500=1200
2÷0.01=200 10﹣5.91=4.09 a+0.8a=1.8a 0.92=0.81
7.85×0.9×0=0 0.5×4÷0.5×4=16
【点评】本题考查了小数的乘除法的计算法则的应用。
17.(8分)列竖式计算。
2.9×0.56≈(得数保留一位小数)
5.7÷9=(得数用循环小数表示)
【考点】小数除法;小数乘法.
【专题】计算题;运算能力.
【答案】1.6;0.6。
【分析】2.9×0.56,利用小数乘法计算方法去计算,用四舍五入法保留一位小数;
5.7÷9,用小数除法的计算方法,利用循环小数的知识去解答。
【解答】解:2.9×0.56≈1.6
5.7÷9=0.6
【点评】本题考查的是小数乘法,小数除法的计算方法。
18.(8分)计算。
80×0.25×0.4×12.5 7.22×8.4+8.4×2.78
1.7÷0.25÷0.4 6.5+3.5÷0.05
【考点】小数四则混合运算.
【专题】运算能力.
【答案】100,84,17,76.5。
【分析】(1)根据乘法交换律和乘法结合律简算;
(2)根据乘法分配律简算;
(3)根据除法的性质计算;
(4)先算除法,再算加法。
【解答】解:(1)80×0.25×0.4×12.5
=(80×12.5)×(0.25×0.4)
=1000×0.1
=100
(2)7.22×8.4+8.4×2.78
=(7.22+2.78)×8.4
=10×8.4
=84
(3)1.7÷0.25÷0.4
=1.7÷(0.25×0.4)
=1.7÷0.1
=17
(4)6.5+3.5÷0.05
=6.5+70
=76.5
【点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
19.(6分)解方程。
2x+120=200 x﹣54.21=69 x+2.5=3.8
【考点】小数方程求解;整数方程求解.
【专题】应用题;应用意识.
【答案】x=40;x=123.21;x=1.3。
【分析】2x+120=200,根据等式的基本性质,方程两边同时减去120,然后再同时除以2,最后计算即可求出x的值;
x﹣54.21=69,根据等式的基本性质,方程两边同时加上54.21,然后计算即可求出x的值;
x+2.5=3.8,根据等式的基本性质,方程两边同时减去2.5,然后计算即可求出x的值。
【解答】解:2x+120=200
2x+120﹣120=200﹣120
2x=80
2x÷2=80÷2
x=40
x﹣54.21=69
x﹣54.21+54.21=69+54.21
x=123.21
x+2.5=3.8
x+2.5﹣2.5=3.8﹣2.5
x=1.3
【点评】解答此题要运用等式的基本性质。
四.选择题(共7小题,满分14分,每小题2分)
20.(2分)如图竖式虚线框中的部分表示( )
A.36个一 B.36个十分之一
C.36个百分之一 D.36个千分之一
【考点】小数除法.
【专题】运算能力.
【答案】C
【分析】竖式中的36是6×6得到的,6在百分位上表示0.06,完整的算式为6×0.06=0.36。根据小数的意义可知0.36表示36个百分之一。据此解答即可。
【解答】解:6×0.06=0.36。
0.36表示36个百分之一
故选:C。
【点评】本题考查本题考查小数除以整数的意义。
21.(2分)一块长方形菜地,长40米,宽38米。如果把长减少m米,宽不变,面积将减少 38m 平方米,周长减少 2m 米。
【考点】长方形、正方形的面积.
【专题】应用意识.
【答案】38m,2m。
【分析】根据长方形的面积=长×宽,长方形的周长=(长+宽)×2,如果宽不变,长减少m米,面积将减少38m平方米,周长减少2m米,据此解答。
【解答】解:38×m=38m(平方米)
m×2=2m(米)
答:面积将减少38m平方米,周长减少2m米。
故答案为:38m,2m。
【点评】此题主要考查长方形的面积公式、周长公式的灵活运用,关键是熟记公式。
22.(2分)(1)一辆汽车t时行驶了300km,平均每时行 km;李师傅每时加工40个零件,加工了a时,一共加工了 40a 个零件。
(2)林叔叔和张叔叔是快递员,林叔叔每天送m件快递,张叔叔每天比林叔叔多送20件快递,m+20表示 张叔叔每天送快递的数量 ,5(m+20)表示 张叔叔5天送快递的数量 。
【考点】用字母表示数;简单的行程问题.
【专题】用字母表示数;行程问题;应用意识.
【答案】(1);40a;(2)张叔叔每天送快递的数量;5天送快递的数量。
【分析】(1)速度=路程÷时间,据此计算即可;工作总量=工作效率×工作时间,据此计算即可;
(2)m+20表示张叔叔每天送快递的数量,5(m+20)表示张叔叔5天送快递的数量。
【解答】解:(1)300÷t(千米)
40×a=40a(个)
(2)m+20表示张叔叔每天送快递的数量,5(m+20)表示张叔叔5天送快递的数量。
故答案为:(1);40a;(2)张叔叔每天送快递的数量;5天送快递的数量。
【点评】此题考查用字母表示数和简单的行程问题。掌握用字母表示数的方法和速度、时间、路程之间的数量关系是解答的关键。
23.(2分)直角三角形ABC中,直角边BC长8厘米,AB长3厘米,点A以2厘米/秒的速度向右平移,形成一个梯形(如图),经过 2 秒,梯形的面积会达到18平方厘米。
【考点】梯形的面积.
【专题】应用题;几何直观;应用意识.
【答案】2。
【分析】理由梯形面积公式:S=(a+b)h÷2计算出AA′的长度,再除以2计算经过的时间即可。
【解答】解:18×2÷3﹣8
=36÷3﹣8
=12=8
=4(厘米)
4÷2=2(秒)
答:经过2秒,梯形的面积会达到18平方厘米。
故答案为:2。
【点评】本题考查了梯形的面积公式的灵活运用。
24.(2分)如图,A点用数对表示为(4,4),B点用数对表示为 (3,1) ,C点用数对表示为 (6,4) 。
【考点】数对与位置.
【专题】综合题;几何直观.
【答案】(3,1),(6,4)。
【分析】用数对表示位置时,先表示第几列,再表示第几行,依据题意结合图示去解答。
【解答】解:如图:
B点用数对表示为(3,1),C点用数对表示为(6,4)。
故答案为:(3,1),(6,4)。
【点评】本题考查的是数对与位置的应用。
25.(2分)已知下图中阴影部分的面积是18平方厘米,空白部分的面积是 27 平方厘米。
【考点】组合图形的面积.
【专题】几何直观;应用意识.
【答案】27。
【分析】由三角形的面积=底×高÷2,可知高=三角形的面积×2÷底,由此求出阴影部分三角形的高(空白部分梯形的高),梯形的上底是15﹣12=3(厘米),下底是15厘米,根据梯形的面积=(上底+下底)×高÷2,即可求得空白部分的面积。
【解答】解:18×2÷12
=36÷12
=3(厘米)
(15﹣12+15)×3÷2
=18×3÷2
=54÷2
=27(平方厘米)
答:空白部分的面积是27平方厘米。
故答案为:27。
【点评】此题主要考查三角形的面积公式、梯形的面积公式的灵活运用,关键是熟记公式。
26.(2分)如图,这是由4个相同的直角三角形拼成的大正方形。已知直角三角形的两条直角边长分别是4cm和6cm,那么大正方形的面积是 52 cm2。
【考点】组合图形的面积.
【专题】平面图形的认识与计算;空间观念.
【答案】52。
【分析】由图意可知:中间小正方形的边长为6﹣4=2(厘米),则大正方形的面积=直角三角形的面积×4+小正方形的面积,代入数据即可求解。
【解答】解:6×4÷2×4+(6﹣4)×(6﹣4)
=48+4
=52(平方厘米)
答:大正方形的面积是52平方厘米。
故答案为:52。
【点评】由三角形的直角边长求出小正方形的边长,是解答本题的关键。
五.应用题(共6小题,满分26分)
27.(4分)张叔叔乘坐汕头出租车行驶了8.4km,使用手机付款,且有一个可用的3.05元的“红包”,张叔叔实际支付多少元?
里程 收费标准
3km及以内 9元
超过3km的部分 每千米2.4元 (不足1km,按1km计算)
【考点】整数、小数复合应用题.
【专题】应用题;应用意识.
【答案】20.35元。
【分析】本题解题关键是先计算出超过3千米的部分,再根据总价=单价×数量,计算出超过3千米的部分所花的钱数,再用3千米以内的钱数加上超过3千米的部分所花的钱数,再减去3.05元即可。
【解答】解:8.4﹣3=5.4(米)
5.4米按6米算。
6×2.4+9﹣3.05
=14.4+9﹣3.05
=23.4﹣3.05
=20.35(元)
答:张叔叔实际支付20.35元。
【点评】本题考查分段付费问题的解题方法,解题关键是找准收费标准,然后明晰是怎样进行分段付费的,把各段的费用分别计算出来,再相加。
28.(4分)小华在帮妈妈核实消费账单时,把账单上的5.3元看成了5.8元,结果得到的总金额为10元,与账单对不上,正确的结果是多少呢?
【考点】整数、小数复合应用题.
【专题】应用题;应用意识.
【答案】9.5元。
【分析】核实消费账单总金额时使用加法,小华把其中一个加数“5.3”看成了“5.8”,多加了5.8﹣5.3=0.5(元),即最后的总金额比正确结果多了0.5 元,再用总金额减去0.5元即可解答。
【解答】解:5.8﹣5.3=0.5(元)
10﹣0.5=9.5 (元)
答:正确的结果是9.5元。
【点评】此题考查小数减法计算及应用。
29.(6分)圆形湖的周长是1350米,沿湖边每隔9米种一棵柳树,在两棵柳树之间等距离种桃树2棵。一共种了多少棵桃树?
【考点】植树问题.
【专题】应用意识.
【答案】300棵。
【分析】围成一个圆圈植树时,植树棵数=间隔数,由此先计算出间隔数,从而得出柳树的棵数,再用柳树的棵数乘2就是种桃树的棵数,据此解答。
【解答】解:1350÷9×2
=150×2
=300(棵)
答:一共种了300棵桃树。
【点评】解答本题的关键是根据植树棵数=间隔数计算出柳树的棵数,从而进一步来求解桃树的棵数。
30.(4分)重庆居民生活用电规定:每月不超过200千瓦时(含200千瓦时),按每千瓦时0.52元收取电费;超过200千瓦时的部分按每千瓦时0.57元收取电费。若8月份文乐家共花费149.6元电费,则文乐家8月份用电多少千瓦时?
【考点】整数、小数复合应用题.
【专题】应用题;运算能力.
【答案】280。
【分析】根据电费计价规则,200千瓦时以内每千瓦时0.52元,即该电价下的电费最多为200×0.52=104(元),文乐家8月份电费为149.6元,超出了104元,说明用电量超出了200千瓦时,用149.6元减去104元,再除以超出部分的电价0.57元/千瓦时,即可求出超出200千瓦时部分的用电量,再加上200千瓦时即可求出文乐家8月份的用电量。
【解答】解:200×0.52=104(元)
(149.6﹣104)÷0.57+200
=45.6÷0.57+200
=80+200
=280(千瓦时)
答:文乐家8月份用电280千瓦时。
【点评】本题有一定的综合性,关键是要理解电价的计费规则和分段计价的计费模式。
31.(4分)佳佳挑出了26块饼干,打算把它们装袋送给朋友们品尝。有两种包装袋,一种是塑料袋,每袋装5块,另一种是纸袋,每袋装3块。如果每袋都装满,怎样装能恰好装完?把装饼干的方案填写在如表中并答题。
方案序号 塑料袋(每袋装5块) 纸袋(每袋装3块) 饼干块数
① 6袋 0袋 5×6=30(块)
② 5袋 1袋 5×5+3×1=28(块)
③
④
⑤
⑥
⑦
【考点】数表中的规律.
【专题】应用意识.
【答案】装4袋塑料袋和2袋纸袋或1袋塑料袋和7袋纸袋。
【分析】利用列举法找到合适的装袋方案,回答问题即可。
【解答】解:
方案序号 塑料袋(每袋装5块) 纸袋(每袋装3块) 饼干块数
① 6袋 0袋 5×6=30(块)
② 5袋 1袋 5×5+3×1=28(块)
③ 4袋 2袋 5×4+3×2=26(块)
④ 3袋 4袋 5×3+3×4=27(块)
⑤ 2袋 6袋 5×2+3×6=28(块)
⑥ 1袋 7袋 5×1+3×7=26(块)
⑦ 0袋 9袋 3×9=27(块)
答:如果每袋都装满,可以装4袋塑料袋和2袋纸袋或1袋塑料袋和7袋纸袋。
【点评】本题主要考查列举法解决问题的方法的应用。
32.(4分)一块菜地的形状如图(阴影部分),图中每个小方格的边长为1m,那么这块菜地的面积是多少平方米?
【考点】组合图形的面积.
【专题】平面图形的认识与计算;空间观念.
【答案】见试题解答内容
【分析】把这块菜地的面积分割成两个图形的面积,一个梯形,一个三角形,把梯形与三角形的面积相加即可.
【解答】解:
菜地的面积5×4+(5+2)×4÷2
=10+14
=24(平方米)
答:这快菜地的面积是24平方米.
【点评】本题考查图形的转化,把一个不规则的图形转化成我们熟悉的图形进行解答,本题运用了三角形的面积公式及梯形的面积公式进行解答.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省杭州市2025-2026学年五年级上学期期末模拟数学预测卷
一.填空题(共9小题,满分18分,每小题2分)
1.(2分)根据算式23×16=368,直接写出得数。
0.23×1.6= 230×0.16= 0.23×0.16=
2.(2分)
(1)一包饼干和一袋瓜子一共多少元?
(2)一袋果冻比一盒薯片贵多少元?
(3)奇思想买一袋面包和一袋果冻,他只有8元,够吗?
(4)妙想有5元,可以买哪两种食物?请给出两种买法。
第一种食物价钱 第二种食物价钱 合计钱数 剩余钱数
买法一
买法二
3.(2分)甲数是乙数的13倍,甲数除以乙数的商是 ;如果甲数扩大到原来的8倍,要使商不变,乙数应 。
4.(2分)在横线里填上“>”“<”或“=”。
0.84÷1.5 0.84
2.12÷0.4 2.12×0.4
5.(2分)一根彩带长19.2米,把它对折三次,平均每段长 分米。
6.(2分)一桶乒乓球有a个。
3元/个 2.7g/个
(1)体育老师又买来了3个,现在有 个乒乓球;
(2)塑料桶重100g,原来这一桶乒乓球连瓶共重 g;
(3)如果这一桶乒乓球连瓶共重154g,买来的时候是整桶购买的,花费50元,那么每个便宜了
元。
7.(2分)根据规律写出答案。
1×1=1
11×11=121
111×111=12321
1111×1111=1234321
11111×11111=
8.(2分)如图,在一个梯形中剪去一个最大的平行四边形,这个平行四边形的面积是 平方厘米,剩下的图形的面积是 平方厘米。
9.(2分)在框里填上合适的数。
二.选择题(共6小题,满分12分,每小题2分)
10.(2分)下列方程中,与1.8x﹣1.2=2.4的解不相等的是( )
A.1.8x=2.4+1.2 B.1.8x﹣2.4=1.2
C.1.8x=2.4﹣1.2 D.18x﹣12=24
11.(2分)两个因数都是0.9,写成算式是( )
A.0.9×2 B.0.9×0.9 C.0.9+0.9 D.0.9﹣0.9
12.(2分)如图中,两个正方形的边长都是5分米,阴影部分的面积是( )
A.10dm2 B.15dm2 C.20dm2 D.25dm2
13.(2分)如图中每个小方格表示边长为1厘米的正方形,曲线所围成图形的面积大约是( )厘米2。
A.70 B.50 C.40 D.30
14.(2分)从一副扑克牌中任意抽出一张,那么抽出的一张中,( )
A.大王或小王的可能性最小。
B.是梅花或方块的可能性大些。
C.红桃或黑桃的可能性大些。
15.(2分)一台学习机原价是701元,现价是598元,大约便宜了( )元。
A.100 B.103 C.200
三.计算题(共4小题,满分30分)
16.(8分)直接写得数。
5.6÷7= 39×0.2= 1÷0.25= 2.4×500=
2÷0.01= 10﹣5.91= a+0.8a= 0.92=
7.85×0.9×0= 0.5×4÷0.5×4=
17.(8分)列竖式计算。
2.9×0.56≈(得数保留一位小数)
5.7÷9=(得数用循环小数表示)
18.(8分)脱式计算。
80×0.25×0.4×12.5 7.22×8.4+8.4×2.78
1.7÷0.25÷0.4 6.5+3.5÷0.05
19.(6分)解方程。
2x+120=200 x﹣54.21=69 x+2.5=3.8
四.选择题(共7小题,满分14分,每小题2分)
20.(2分)如图竖式虚线框中的部分表示( )
A.36个一 B.36个十分之一
C.36个百分之一 D.36个千分之一
21.(2分)一块长方形菜地,长40米,宽38米。如果把长减少m米,宽不变,面积将减少 平方米,周长减少 米。
22.(2分)(1)一辆汽车t时行驶了300km,平均每时行 km;李师傅每时加工40个零件,加工了a时,一共加工了 个零件。
(2)林叔叔和张叔叔是快递员,林叔叔每天送m件快递,张叔叔每天比林叔叔多送20件快递,m+20表示 ,5(m+20)表示 。
23.(2分)直角三角形ABC中,直角边BC长8厘米,AB长3厘米,点A以2厘米/秒的速度向右平移,形成一个梯形(如图),经过 秒,梯形的面积会达到18平方厘米。
24.(2分)如图,A点用数对表示为(4,4),B点用数对表示为 ,C点用数对表示为 。
25.(2分)已知下图中阴影部分的面积是18平方厘米,空白部分的面积是 平方厘米。
26.(2分)如图,这是由4个相同的直角三角形拼成的大正方形。已知直角三角形的两条直角边长分别是4cm和6cm,那么大正方形的面积是 cm2。
五.应用题(共6小题,满分26分)
27.(4分)张叔叔乘坐汕头出租车行驶了8.4km,使用手机付款,且有一个可用的3.05元的“红包”,张叔叔实际支付多少元?
里程 收费标准
3km及以内 9元
超过3km的部分 每千米2.4元 (不足1km,按1km计算)
28.(4分)小华在帮妈妈核实消费账单时,把账单上的5.3元看成了5.8元,结果得到的总金额为10元,与账单对不上,正确的结果是多少呢?
29.(6分)圆形湖的周长是1350米,沿湖边每隔9米种一棵柳树,在两棵柳树之间等距离种桃树2棵。一共种了多少棵桃树?
30.(4分)重庆居民生活用电规定:每月不超过200千瓦时(含200千瓦时),按每千瓦时0.52元收取电费;超过200千瓦时的部分按每千瓦时0.57元收取电费。若8月份文乐家共花费149.6元电费,则文乐家8月份用电多少千瓦时?
31.(4分)佳佳挑出了26块饼干,打算把它们装袋送给朋友们品尝。有两种包装袋,一种是塑料袋,每袋装5块,另一种是纸袋,每袋装3块。如果每袋都装满,怎样装能恰好装完?把装饼干的方案填写在如表中并答题。
方案序号 塑料袋(每袋装5块) 纸袋(每袋装3块) 饼干块数
① 6袋 0袋 5×6=30(块)
② 5袋 1袋 5×5+3×1=28(块)
③
④
⑤
⑥
⑦
32.(4分)一块菜地的形状如图(阴影部分),图中每个小方格的边长为1m,那么这块菜地的面积是多少平方米?
浙江省杭州市2025-2026学年五年级上学期期末模拟数学预测卷
参考答案与试题解析
一.填空题(共9小题,满分18分,每小题2分)
1.(2分)根据算式23×16=368,直接写出得数。
0.23×1.6= 0.368 230×0.16= 36.8 0.23×0.16= 0.0368
【考点】积的变化规律.
【专题】运算能力.
【答案】0.368,36.8,0.0368。
【分析】根据积的变化规律:两数相乘,如果一个因数乘(或除以)几(0除外),另一个因数也乘(或除以)几(0除外),原来的积就乘(或除以)它们的乘积。
【解答】解:根据算式23×16=368,可得:
0.23×1.6=0.368 230×0.16=36.8 0.23×0.16=0.0368
故答案为:0.368,36.8,0.0368。
【点评】本题考查的是积的变化规律,准确判断因数发生的变化是解决本题的关键。
2.(2分)
(1)一包饼干和一袋瓜子一共多少元?
(2)一袋果冻比一盒薯片贵多少元?
(3)奇思想买一袋面包和一袋果冻,他只有8元,够吗?
(4)妙想有5元,可以买哪两种食物?请给出两种买法。
第一种食物价钱 第二种食物价钱 合计钱数 剩余钱数
买法一
1.20
2.50
3.70
1.30
买法二
2.50
0.80
3.30
1.70
【考点】整数、小数复合应用题.
【专题】综合题;应用意识.
【答案】(1)6.30元;
(2)2.10元;
(3)不够;
(4)
第一种食物价钱 第二种食物价钱 合计钱数 剩余钱数
买法一 1.20 2.50 3.70 1.30
买法二 2.50 0.80 3.30 1.70
(答案不唯一)
【分析】(1)用加法列式计算一包饼干和一袋瓜子一共多少元;
(2)用减法列式计算一袋果冻比一盒薯片贵多少元;
(3)用加法列式计算买一袋面包和一袋果冻的价钱,然后和8元比较大小;
(4)两种食物的价钱不超过5元就符合要求,由此解答本题(答案不唯一)。
【解答】解:(1)3.80+2.50=6.30(元)
答:一包饼干和一袋瓜子一共6.30元。
(2)6.50﹣4.40=2.10(元)
答:一袋果冻比一盒薯片贵2.10元。
(3)1.80+6.50=8.30(元)
8.30>8
答:奇思想买一袋面包和一袋果冻,8元不够。
(4)1.20+2.50=3.70(元)
5﹣3.70=1.30(元)
2.50+0.80=3.30(元)
5﹣3.30=1.70(元)
第一种食物价钱 第二种食物价钱 合计钱数 剩余钱数
买法一 1.20 2.50 3.70 1.30
买法二 2.50 0.80 3.30 1.70
(答案不唯一)
【点评】解决本题的关键是找出题中的数量关系,利用数量关系列式计算。
3.(2分)甲数是乙数的13倍,甲数除以乙数的商是 13 ;如果甲数扩大到原来的8倍,要使商不变,乙数应 扩大到原来的8倍 。
【考点】商的变化规律.
【专题】运算能力.
【答案】13,扩大到原来的8倍。
【分析】在除法算式中,被除数和除数同时扩大或缩小相同的倍数(0除外),商不变;据此解答即可。
【解答】解:甲数是乙数的13倍,甲数除以乙数的商是13。
根据商不变的性质可知,如果甲数扩大到原来的8倍,要使商不变,乙数应扩大到原来的8倍。
故答案为:13,扩大到原来的8倍。
【点评】解答此题应明确:只有被除数和除数同时扩大或缩小相同的倍数(0除外),商才不变。
4.(2分)在横线里填上“>”“<”或“=”。
0.84÷1.5 < 0.84
2.12÷0.4 > 2.12×0.4
【考点】商的变化规律;积的变化规律.
【专题】数据分析观念.
【答案】<,>。
【分析】一个数(0除外)除以一个大于1的数,商小于原数;一个数(0除外)除以一个小于1的数,商大于原数;一个数(0除外)乘一个小于1的数,积小于原数。据此解答。
【解答】解:0.84÷1.5<0.84
2.12÷0.4>2.12×0.4
故答案为:<,>。
【点评】熟练掌握商的变化规律和积的变化规律是解题的关键。
5.(2分)一根彩带长19.2米,把它对折三次,平均每段长 24 分米。
【考点】小数除法.
【专题】综合填空题;应用意识.
【答案】24。
【分析】对折三次,则这根彩带被平均分成8段,用除法列式计算平均每段长多少分米。
【解答】解:19.2米=192分米,对折三次,则这根彩带被平均分成8段,每段长度:192÷8=24(分米)
故答案为:24。
【点评】解决本题的关键是找出题中数量关系。
6.(2分)一桶乒乓球有a个。
3元/个 2.7g/个
(1)体育老师又买来了3个,现在有 (a+3) 个乒乓球;
(2)塑料桶重100g,原来这一桶乒乓球连瓶共重 (100+2.7a) g;
(3)如果这一桶乒乓球连瓶共重154g,买来的时候是整桶购买的,花费50元,那么每个便宜了 (3﹣50÷a) 元。
【考点】用字母表示数;整数、小数复合应用题.
【专题】运算能力;应用意识.
【答案】(1)(a+3);(2)(100+2.7a);(3)(3﹣50÷a)。
【分析】(1)现在有乒乓球的个数=原来一桶乒乓球的个数+体育老师又买来的个数;
(2)原来这一桶乒乓球连瓶一共的质量=塑料桶的质量+平均每个乒乓的质量×原来的个数;
(3)每个便宜的钱数=零售价﹣整桶买的单价;其中,整桶买的单价=总价÷整桶的个数。
【解答】解:(1)(a+3)个
体育老师又买来了3个,现在有(a+3)个乒乓球。
(2)100+2.7×a=(100+2.7a)g
塑料桶重100g,原来这一桶乒乓球连瓶共重(100+2.7)g。
(3)(3﹣50÷a)元
如果这一桶乒乓球连瓶共重154g,买来的时候是整桶购买的,花费50元,那么每个便宜了(3﹣50÷a)元。
故答案为:(a+3);(100+2.7a);(3﹣50÷a)。
【点评】本题考查用字母表示数,关键是弄清楚它们之间的关系。
7.(2分)根据规律写出答案。
1×1=1
11×11=121
111×111=12321
1111×1111=1234321
11111×11111= 123454321
【考点】“式”的规律.
【专题】规律型;探索数的规律;运算能力.
【答案】123454321。
【分析】1×1=1
11×11=121
111×111=12321
1111×1111=1234321
因数各个位上的数字都是1,当因数是n位数时,积各个位上数字是由1排到n,再由n排到1,即:123……n……321;据此解答即可。
【解答】解:1×1=1
11×11=121
111×111=12321
1111×1111=1234321
11111×11111=123454321
故答案为:123454321。
【点评】主要考查了“式”的规律,同时考查了学生的分析、总结、归纳能力,规律型的习题一般是从所给的数据和运算方法进行分析,从特殊值的规律上总结出一般性的规律。
8.(2分)如图,在一个梯形中剪去一个最大的平行四边形,这个平行四边形的面积是 120 平方厘米,剩下的图形的面积是 60 平方厘米。
【考点】平行四边形的面积;梯形的面积.
【专题】应用题;应用意识.
【答案】120;60。
【分析】由图可知,一个梯形的上底长12厘米,下底长24厘米,高10厘米,若在这个梯形中剪去一个最大的平行四边形,这个平行四边形的底是12厘米,高是10厘米;
剩余部分是一个三角形,这个三角形的底是(24﹣12)厘米,高是10厘米;
根据平行四边形的面积=底×高,三角形的面积=底×高÷2,解答此题即可。
【解答】解:12×10=120(平方厘米)
(24﹣12)×10÷2
=12×10÷2
=120÷2
=60(平方厘米)
答:这个平行四边形的面积是 120平方厘米,剩下的图形的面积是 60平方厘米。
故答案为:120;60。
【点评】熟练掌握平行四边形和三角形的面积公式,是解答此题的关键。
9.(2分)在框里填上合适的数。
【考点】竖式数字谜.
【专题】计算题;运算能力.
【答案】
【分析】第一题,积是469,第一个因数的个位数字是7,7×7=49,所以第二个因数是7,用469÷7得出第一个因数。
第二题,2+7=9,得出被减数是929,然后根据929减482算出减数。
【解答】解:如下所示:
【点评】解答本题的关键是熟练掌握竖式乘法和竖式加法的计算方法,正确找出从哪个数位入手。
二.选择题(共6小题,满分12分,每小题2分)
10.(2分)下列方程中,与1.8x﹣1.2=2.4的解不相等的是( )
A.1.8x=2.4+1.2 B.1.8x﹣2.4=1.2
C.1.8x=2.4﹣1.2 D.18x﹣12=24
【考点】小数方程求解.
【专题】应用题;应用意识.
【答案】C
【分析】根据等式的基本性质,分别求出每个方程的解,然后解答即可。
【解答】解:1.8x﹣1.2=2.4
1.8x=2.4+1.2
1.8x=3.6
x=3.6÷1.8
x=2
1.8x=2.4+1.2
1.8x=3.6
x=3.6÷1.8
x=2
1.8x﹣2.4=1.2
1.8x=2.4+1.2
1.8x=3.6
x=3.6÷1.8
x=2
1.8x=2.4﹣1.2
1.8x=1.2
x=1.2÷1.8
x
18x﹣12=24
18x=12+24
18x=36
x=36÷18
x=2
故选:C。
【点评】解答此题要运用等式的基本性质。
11.(2分)两个因数都是0.9,写成算式是( )
A.0.9×2 B.0.9×0.9 C.0.9+0.9 D.0.9﹣0.9
【考点】小数乘法.
【专题】综合判断题;运算能力.
【答案】B
【分析】根据题意,两个因数都是0.9,可知,一个因数是0.9,另一个因数也是0.9,再根据小数乘法进行列式即可。
【解答】解:根据题意可得:一个因数是0.9,另一个因数也是0.9,所以,算式是:0.9×0.9。
故选:B。
【点评】根据乘法各部分的名称进行解答即可。
12.(2分)如图中,两个正方形的边长都是5分米,阴影部分的面积是( )
A.10dm2 B.15dm2 C.20dm2 D.25dm2
【考点】组合图形的面积.
【专题】几何直观;推理能力;应用意识.
【答案】D
【分析】通过观察图形可知,阴影部分的面积通过平移“转化”为一个正方形的面积,根据正方形的面积=边长×边长,把数据代入公式解答。
【解答】解:5×5=25(平方分米)
答:阴影部分的面积是25平方分米。
故选:D。
【点评】此题主要考查正方形面积公式的灵活运用,关键是通过平移把阴影部分的面积转化我应该正方形的面积。
13.(2分)如图中每个小方格表示边长为1厘米的正方形,曲线所围成图形的面积大约是( )厘米2。
A.70 B.50 C.40 D.30
【考点】用方格纸计算图形面积.
【专题】几何直观.
【答案】B
【分析】根据图示,图中曲线所围成图形近似一个长10厘米,宽5厘米的长方形,根据长方形的面积公式解答即可。
【解答】解:10×5=50(平方厘米)
答:曲线所围成图形的面积大约是50厘米。
故选:B。
【点评】本题考查了面积估算知识,结合题意分析解答即可。
14.(2分)从一副扑克牌中任意抽出一张,那么抽出的一张中,( )
A.大王或小王的可能性最小。
B.是梅花或方块的可能性大些。
C.红桃或黑桃的可能性大些。
【考点】可能性的大小.
【专题】可能性;应用意识.
【答案】A
【分析】根据不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。据此解答即可。
【解答】解:一副扑克牌中,大王和小王各有一张,梅花、方块、红桃、黑桃各有13张;
所以抽出的一张中,梅花、方块、红桃、黑桃的可能性一样,大王或小王的可能性最小。
故选:A。
【点评】解答此题的关键:应明确可能性的计算方法,并能根据实际情况进行灵活运用。
15.(2分)一台学习机原价是701元,现价是598元,大约便宜了( )元。
A.100 B.103 C.200
【考点】数的估算.
【专题】运算能力;应用意识.
【答案】A
【分析】用学习机原件减去现价,把701看作700,598看作600进行估算即可。
【解答】解:701﹣598
≈700﹣600
=100(元)
答:大约便宜了100元。
故选:A。
【点评】本题考查了数的估算,可以把数看作近似整十、整百、整千……的数进行估算。
三.计算题(共4小题,满分30分)
16.(8分)直接写得数。
5.6÷7= 39×0.2= 1÷0.25= 2.4×500=
2÷0.01= 10﹣5.91= a+0.8a= 0.92=
7.85×0.9×0= 0.5×4÷0.5×4=
【考点】小数除法;有理数的乘方;小数乘法.
【专题】运算能力.
【答案】0.8;7.8;4;1200,200;4.09;1.8a;0.81,0;16。
【分析】运用小数的乘除法的计算法则进行计算即可。
【解答】解:
5.6÷7=0.8 39×0.2=7.8 1÷0.25=4 2.4×500=1200
2÷0.01=200 10﹣5.91=4.09 a+0.8a=1.8a 0.92=0.81
7.85×0.9×0=0 0.5×4÷0.5×4=16
【点评】本题考查了小数的乘除法的计算法则的应用。
17.(8分)列竖式计算。
2.9×0.56≈(得数保留一位小数)
5.7÷9=(得数用循环小数表示)
【考点】小数除法;小数乘法.
【专题】计算题;运算能力.
【答案】1.6;0.6。
【分析】2.9×0.56,利用小数乘法计算方法去计算,用四舍五入法保留一位小数;
5.7÷9,用小数除法的计算方法,利用循环小数的知识去解答。
【解答】解:2.9×0.56≈1.6
5.7÷9=0.6
【点评】本题考查的是小数乘法,小数除法的计算方法。
18.(8分)计算。
80×0.25×0.4×12.5 7.22×8.4+8.4×2.78
1.7÷0.25÷0.4 6.5+3.5÷0.05
【考点】小数四则混合运算.
【专题】运算能力.
【答案】100,84,17,76.5。
【分析】(1)根据乘法交换律和乘法结合律简算;
(2)根据乘法分配律简算;
(3)根据除法的性质计算;
(4)先算除法,再算加法。
【解答】解:(1)80×0.25×0.4×12.5
=(80×12.5)×(0.25×0.4)
=1000×0.1
=100
(2)7.22×8.4+8.4×2.78
=(7.22+2.78)×8.4
=10×8.4
=84
(3)1.7÷0.25÷0.4
=1.7÷(0.25×0.4)
=1.7÷0.1
=17
(4)6.5+3.5÷0.05
=6.5+70
=76.5
【点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
19.(6分)解方程。
2x+120=200 x﹣54.21=69 x+2.5=3.8
【考点】小数方程求解;整数方程求解.
【专题】应用题;应用意识.
【答案】x=40;x=123.21;x=1.3。
【分析】2x+120=200,根据等式的基本性质,方程两边同时减去120,然后再同时除以2,最后计算即可求出x的值;
x﹣54.21=69,根据等式的基本性质,方程两边同时加上54.21,然后计算即可求出x的值;
x+2.5=3.8,根据等式的基本性质,方程两边同时减去2.5,然后计算即可求出x的值。
【解答】解:2x+120=200
2x+120﹣120=200﹣120
2x=80
2x÷2=80÷2
x=40
x﹣54.21=69
x﹣54.21+54.21=69+54.21
x=123.21
x+2.5=3.8
x+2.5﹣2.5=3.8﹣2.5
x=1.3
【点评】解答此题要运用等式的基本性质。
四.选择题(共7小题,满分14分,每小题2分)
20.(2分)如图竖式虚线框中的部分表示( )
A.36个一 B.36个十分之一
C.36个百分之一 D.36个千分之一
【考点】小数除法.
【专题】运算能力.
【答案】C
【分析】竖式中的36是6×6得到的,6在百分位上表示0.06,完整的算式为6×0.06=0.36。根据小数的意义可知0.36表示36个百分之一。据此解答即可。
【解答】解:6×0.06=0.36。
0.36表示36个百分之一
故选:C。
【点评】本题考查本题考查小数除以整数的意义。
21.(2分)一块长方形菜地,长40米,宽38米。如果把长减少m米,宽不变,面积将减少 38m 平方米,周长减少 2m 米。
【考点】长方形、正方形的面积.
【专题】应用意识.
【答案】38m,2m。
【分析】根据长方形的面积=长×宽,长方形的周长=(长+宽)×2,如果宽不变,长减少m米,面积将减少38m平方米,周长减少2m米,据此解答。
【解答】解:38×m=38m(平方米)
m×2=2m(米)
答:面积将减少38m平方米,周长减少2m米。
故答案为:38m,2m。
【点评】此题主要考查长方形的面积公式、周长公式的灵活运用,关键是熟记公式。
22.(2分)(1)一辆汽车t时行驶了300km,平均每时行 km;李师傅每时加工40个零件,加工了a时,一共加工了 40a 个零件。
(2)林叔叔和张叔叔是快递员,林叔叔每天送m件快递,张叔叔每天比林叔叔多送20件快递,m+20表示 张叔叔每天送快递的数量 ,5(m+20)表示 张叔叔5天送快递的数量 。
【考点】用字母表示数;简单的行程问题.
【专题】用字母表示数;行程问题;应用意识.
【答案】(1);40a;(2)张叔叔每天送快递的数量;5天送快递的数量。
【分析】(1)速度=路程÷时间,据此计算即可;工作总量=工作效率×工作时间,据此计算即可;
(2)m+20表示张叔叔每天送快递的数量,5(m+20)表示张叔叔5天送快递的数量。
【解答】解:(1)300÷t(千米)
40×a=40a(个)
(2)m+20表示张叔叔每天送快递的数量,5(m+20)表示张叔叔5天送快递的数量。
故答案为:(1);40a;(2)张叔叔每天送快递的数量;5天送快递的数量。
【点评】此题考查用字母表示数和简单的行程问题。掌握用字母表示数的方法和速度、时间、路程之间的数量关系是解答的关键。
23.(2分)直角三角形ABC中,直角边BC长8厘米,AB长3厘米,点A以2厘米/秒的速度向右平移,形成一个梯形(如图),经过 2 秒,梯形的面积会达到18平方厘米。
【考点】梯形的面积.
【专题】应用题;几何直观;应用意识.
【答案】2。
【分析】理由梯形面积公式:S=(a+b)h÷2计算出AA′的长度,再除以2计算经过的时间即可。
【解答】解:18×2÷3﹣8
=36÷3﹣8
=12=8
=4(厘米)
4÷2=2(秒)
答:经过2秒,梯形的面积会达到18平方厘米。
故答案为:2。
【点评】本题考查了梯形的面积公式的灵活运用。
24.(2分)如图,A点用数对表示为(4,4),B点用数对表示为 (3,1) ,C点用数对表示为 (6,4) 。
【考点】数对与位置.
【专题】综合题;几何直观.
【答案】(3,1),(6,4)。
【分析】用数对表示位置时,先表示第几列,再表示第几行,依据题意结合图示去解答。
【解答】解:如图:
B点用数对表示为(3,1),C点用数对表示为(6,4)。
故答案为:(3,1),(6,4)。
【点评】本题考查的是数对与位置的应用。
25.(2分)已知下图中阴影部分的面积是18平方厘米,空白部分的面积是 27 平方厘米。
【考点】组合图形的面积.
【专题】几何直观;应用意识.
【答案】27。
【分析】由三角形的面积=底×高÷2,可知高=三角形的面积×2÷底,由此求出阴影部分三角形的高(空白部分梯形的高),梯形的上底是15﹣12=3(厘米),下底是15厘米,根据梯形的面积=(上底+下底)×高÷2,即可求得空白部分的面积。
【解答】解:18×2÷12
=36÷12
=3(厘米)
(15﹣12+15)×3÷2
=18×3÷2
=54÷2
=27(平方厘米)
答:空白部分的面积是27平方厘米。
故答案为:27。
【点评】此题主要考查三角形的面积公式、梯形的面积公式的灵活运用,关键是熟记公式。
26.(2分)如图,这是由4个相同的直角三角形拼成的大正方形。已知直角三角形的两条直角边长分别是4cm和6cm,那么大正方形的面积是 52 cm2。
【考点】组合图形的面积.
【专题】平面图形的认识与计算;空间观念.
【答案】52。
【分析】由图意可知:中间小正方形的边长为6﹣4=2(厘米),则大正方形的面积=直角三角形的面积×4+小正方形的面积,代入数据即可求解。
【解答】解:6×4÷2×4+(6﹣4)×(6﹣4)
=48+4
=52(平方厘米)
答:大正方形的面积是52平方厘米。
故答案为:52。
【点评】由三角形的直角边长求出小正方形的边长,是解答本题的关键。
五.应用题(共6小题,满分26分)
27.(4分)张叔叔乘坐汕头出租车行驶了8.4km,使用手机付款,且有一个可用的3.05元的“红包”,张叔叔实际支付多少元?
里程 收费标准
3km及以内 9元
超过3km的部分 每千米2.4元 (不足1km,按1km计算)
【考点】整数、小数复合应用题.
【专题】应用题;应用意识.
【答案】20.35元。
【分析】本题解题关键是先计算出超过3千米的部分,再根据总价=单价×数量,计算出超过3千米的部分所花的钱数,再用3千米以内的钱数加上超过3千米的部分所花的钱数,再减去3.05元即可。
【解答】解:8.4﹣3=5.4(米)
5.4米按6米算。
6×2.4+9﹣3.05
=14.4+9﹣3.05
=23.4﹣3.05
=20.35(元)
答:张叔叔实际支付20.35元。
【点评】本题考查分段付费问题的解题方法,解题关键是找准收费标准,然后明晰是怎样进行分段付费的,把各段的费用分别计算出来,再相加。
28.(4分)小华在帮妈妈核实消费账单时,把账单上的5.3元看成了5.8元,结果得到的总金额为10元,与账单对不上,正确的结果是多少呢?
【考点】整数、小数复合应用题.
【专题】应用题;应用意识.
【答案】9.5元。
【分析】核实消费账单总金额时使用加法,小华把其中一个加数“5.3”看成了“5.8”,多加了5.8﹣5.3=0.5(元),即最后的总金额比正确结果多了0.5 元,再用总金额减去0.5元即可解答。
【解答】解:5.8﹣5.3=0.5(元)
10﹣0.5=9.5 (元)
答:正确的结果是9.5元。
【点评】此题考查小数减法计算及应用。
29.(6分)圆形湖的周长是1350米,沿湖边每隔9米种一棵柳树,在两棵柳树之间等距离种桃树2棵。一共种了多少棵桃树?
【考点】植树问题.
【专题】应用意识.
【答案】300棵。
【分析】围成一个圆圈植树时,植树棵数=间隔数,由此先计算出间隔数,从而得出柳树的棵数,再用柳树的棵数乘2就是种桃树的棵数,据此解答。
【解答】解:1350÷9×2
=150×2
=300(棵)
答:一共种了300棵桃树。
【点评】解答本题的关键是根据植树棵数=间隔数计算出柳树的棵数,从而进一步来求解桃树的棵数。
30.(4分)重庆居民生活用电规定:每月不超过200千瓦时(含200千瓦时),按每千瓦时0.52元收取电费;超过200千瓦时的部分按每千瓦时0.57元收取电费。若8月份文乐家共花费149.6元电费,则文乐家8月份用电多少千瓦时?
【考点】整数、小数复合应用题.
【专题】应用题;运算能力.
【答案】280。
【分析】根据电费计价规则,200千瓦时以内每千瓦时0.52元,即该电价下的电费最多为200×0.52=104(元),文乐家8月份电费为149.6元,超出了104元,说明用电量超出了200千瓦时,用149.6元减去104元,再除以超出部分的电价0.57元/千瓦时,即可求出超出200千瓦时部分的用电量,再加上200千瓦时即可求出文乐家8月份的用电量。
【解答】解:200×0.52=104(元)
(149.6﹣104)÷0.57+200
=45.6÷0.57+200
=80+200
=280(千瓦时)
答:文乐家8月份用电280千瓦时。
【点评】本题有一定的综合性,关键是要理解电价的计费规则和分段计价的计费模式。
31.(4分)佳佳挑出了26块饼干,打算把它们装袋送给朋友们品尝。有两种包装袋,一种是塑料袋,每袋装5块,另一种是纸袋,每袋装3块。如果每袋都装满,怎样装能恰好装完?把装饼干的方案填写在如表中并答题。
方案序号 塑料袋(每袋装5块) 纸袋(每袋装3块) 饼干块数
① 6袋 0袋 5×6=30(块)
② 5袋 1袋 5×5+3×1=28(块)
③
④
⑤
⑥
⑦
【考点】数表中的规律.
【专题】应用意识.
【答案】装4袋塑料袋和2袋纸袋或1袋塑料袋和7袋纸袋。
【分析】利用列举法找到合适的装袋方案,回答问题即可。
【解答】解:
方案序号 塑料袋(每袋装5块) 纸袋(每袋装3块) 饼干块数
① 6袋 0袋 5×6=30(块)
② 5袋 1袋 5×5+3×1=28(块)
③ 4袋 2袋 5×4+3×2=26(块)
④ 3袋 4袋 5×3+3×4=27(块)
⑤ 2袋 6袋 5×2+3×6=28(块)
⑥ 1袋 7袋 5×1+3×7=26(块)
⑦ 0袋 9袋 3×9=27(块)
答:如果每袋都装满,可以装4袋塑料袋和2袋纸袋或1袋塑料袋和7袋纸袋。
【点评】本题主要考查列举法解决问题的方法的应用。
32.(4分)一块菜地的形状如图(阴影部分),图中每个小方格的边长为1m,那么这块菜地的面积是多少平方米?
【考点】组合图形的面积.
【专题】平面图形的认识与计算;空间观念.
【答案】见试题解答内容
【分析】把这块菜地的面积分割成两个图形的面积,一个梯形,一个三角形,把梯形与三角形的面积相加即可.
【解答】解:
菜地的面积5×4+(5+2)×4÷2
=10+14
=24(平方米)
答:这快菜地的面积是24平方米.
【点评】本题考查图形的转化,把一个不规则的图形转化成我们熟悉的图形进行解答,本题运用了三角形的面积公式及梯形的面积公式进行解答.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
