4.5 相似三角形判定定理的证明 同步练习(含答案)
文档属性
| 名称 | 4.5 相似三角形判定定理的证明 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 351.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-09 13:42:10 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
5 相似三角形判定定理的证明
一、单选题
1.(2024九上·杭州月考)如图,下列条件不能判定的是( )
A. B.
C. D.
2.(2024九上·荔城期末)如图,在中,为上一点,若,则( )
A.~ B.~
C.~ D.无法判断
3.(2021九上·滨海月考)下列命题中,错误的是( )
A.所有的正多边形都相似
B.有一对锐角相等的两个直角三角形相似
C.全等的三角形一定相似
D.所有的等边三角形都相似
4.(2023九上·东昌府月考)如图,在中,点D、E分别在边上,与边不平行,那么下列条件中,能判定是( )
A. B.
C. D.
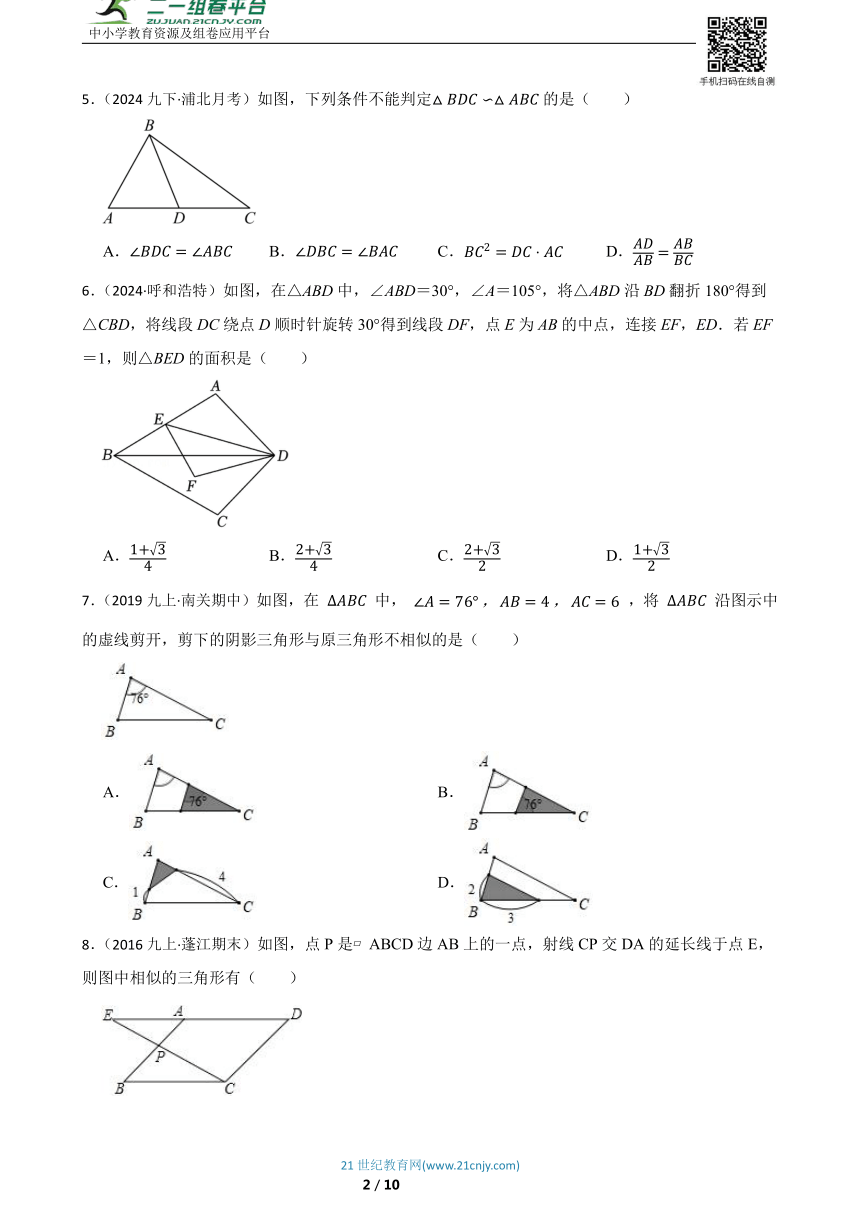
5.(2024九下·浦北月考)如图,下列条件不能判定的是( )
A. B. C. D.
6.(2024·呼和浩特)如图,在△ABD中,∠ABD=30°,∠A=105°,将△ABD沿BD翻折180°得到△CBD,将线段DC绕点D顺时针旋转30°得到线段DF,点E为AB的中点,连接EF,ED.若EF=1,则△BED的面积是( )
A. B. C. D.
7.(2019九上·南关期中)如图,在 中, ,将 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B.
C. D.
8.(2016九上·蓬江期末)如图,点P是 ABCD边AB上的一点,射线CP交DA的延长线于点E,则图中相似的三角形有( )
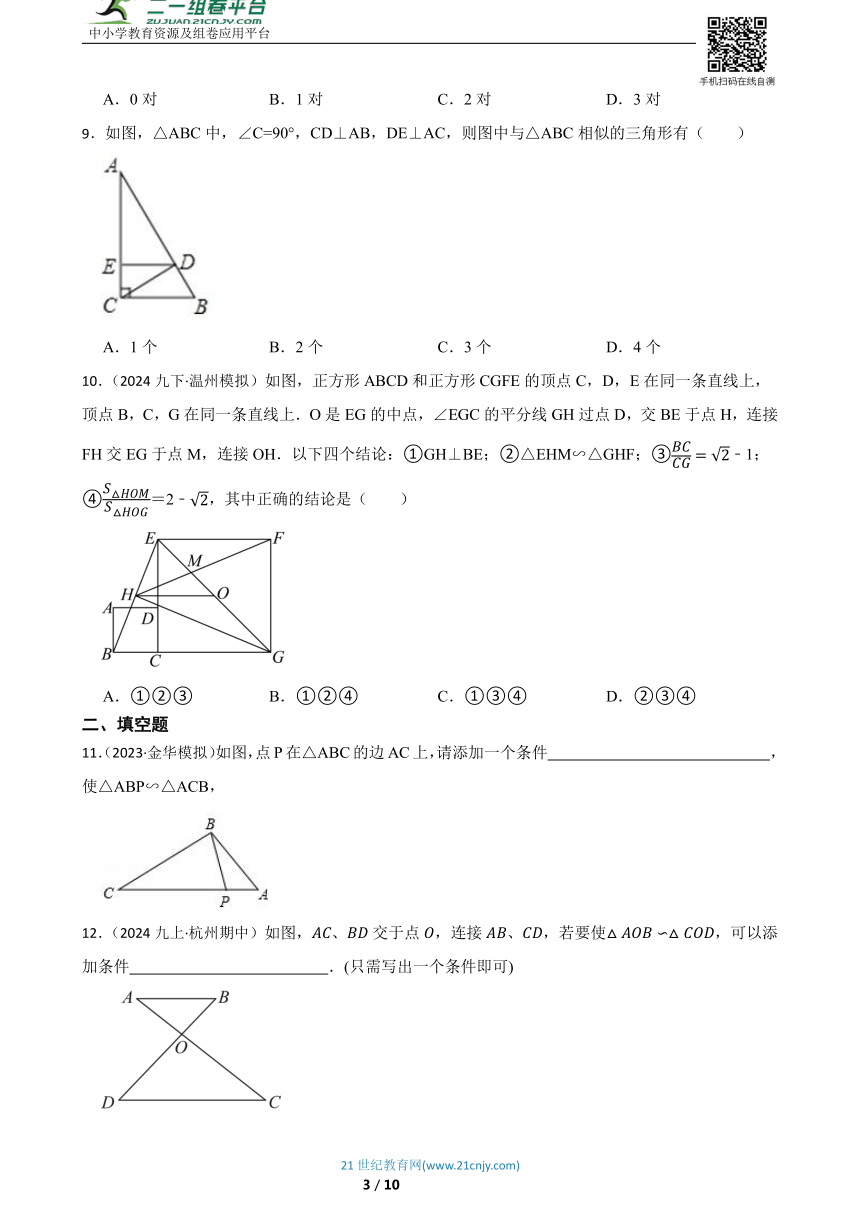
A.0对 B.1对 C.2对 D.3对
9.如图,△ABC中,∠C=90°,CD⊥AB,DE⊥AC,则图中与△ABC相似的三角形有( )
A.1个 B.2个 C.3个 D.4个
10.(2024九下·温州模拟)如图,正方形ABCD和正方形CGFE的顶点C,D,E在同一条直线上,顶点B,C,G在同一条直线上.O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接FH交EG于点M,连接OH.以下四个结论:①GH⊥BE;②△EHM∽△GHF;③﹣1;④=2﹣,其中正确的结论是( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题
11.(2023·金华模拟)如图,点P在△ABC的边AC上,请添加一个条件 ,使△ABP∽△ACB,
12.(2024九上·杭州期中)如图,、交于点,连接、,若要使,可以添加条件 .(只需写出一个条件即可)
13.(2023九上·鄞州月考)如图,已知,请添加一个条件 (只需填写一个即可),使得.
14.(2016九上·北京期中)如图,∠DAB=∠CAE,要使△ABC∽△ADE,则补充的一个条件可以是 (注:只需写出一个正确答案即可).
15.如图,在矩形ABCD中,AB= 4,AD= 8,点E,F分别在边AD,BC上,且AE= 3,按以下步骤操作:
第一步,沿直线EF翻折,点A的对应点A' 恰好落在对角线AC上,点B的对应点为B' ,则线段BF的长为 ;
第二步,分别在EF,AB' '上取点M,N,沿直线MN继续翻折,使点F与点E重合,则线段MN的长为 .
16.(2025九下·江海模拟)如图是一张矩形纸片,点是中点,点在上,把该纸片沿折叠,点的对应点分别为,的延长线经过点,与相交于点.若,且点平分,则的长为 .
三、计算题
17.(2024九上·苏州期末)如图,在菱形中,过D作交的延长线于点E,过E作交于点F.
(1)求证;
(2)若,求的长.
四、解答题
18.(2024九上·定州期末)如图,在△ABC中,AB=10,AC=8,点D,E分别是边AB、AC上的点,且AD=4,∠BDE+∠C=180°,求AE的长.
19.已知一个三角形三边的长分别为6cm,9cm,7.5cm,另一个三角形三边的长分别为8cm,10cm,12cm.试判断这两个三角形是否相似,并说明理由.
20.已知:如图,∠DAB=∠EAC,∠ADE=∠ABC.求证:
(1)△ADE∽△ABC.
(2)△ADB∽△AEC.
21.(2025九下·南山期中)问题提出
(1)如图,在中,,的面积为在内作一个正方形,使正方形一边落在边上,另外两个顶点,分别落在边,上,该正方形的面积大小为 ▲ .
问题解决
(2)某市进行绿化改造,美化生态环境如图,现有一块四边形的空地计划改造成公园,经测量,,,,且按设计要求,要在四边形公园内建造一个矩形活动场所,顶点,均在边上,顶点,分别在边,上为了满足居民需求,计划在矩形活动场所中种植草坪,在公园内其他区域种植花卉已知花卉每平方米元,草坪每平方米元,则绿化改造所需费用至少为多少元?结果保留整数,参考数据
答案解析部分
1.【答案】C
【知识点】相似三角形的判定
2.【答案】C
【知识点】相似三角形的判定
3.【答案】A
【知识点】相似多边形;相似三角形的判定
4.【答案】C
【知识点】相似三角形的判定
5.【答案】D
【知识点】相似三角形的判定
6.【答案】A
【知识点】三角形的面积;相似三角形的判定;三角形全等的判定-SAS
7.【答案】D
【知识点】相似三角形的判定
8.【答案】D
【知识点】平行四边形的性质;相似三角形的判定
9.【答案】D
【知识点】相似三角形的判定
10.【答案】A
【知识点】三角形全等及其性质;正方形的判定与性质;三角形全等的判定-SAS;相似三角形的判定-AA;相似三角形的性质-对应边
11.【答案】∠C=∠ABP(答案不唯一)
【知识点】相似三角形的判定
12.【答案】(答案不唯一)
【知识点】相似三角形的判定
13.【答案】或或(其中任何一个条件即可)
【知识点】相似三角形的判定
14.【答案】∠B=∠D
【知识点】相似三角形的判定
15.【答案】1;
【知识点】勾股定理;矩形的性质;翻折变换(折叠问题);相似三角形的判定;相似三角形的性质-对应边
16.【答案】
【知识点】矩形的性质;翻折变换(折叠问题);相似三角形的判定-AA;相似三角形的性质-对应边
17.【答案】(1)证明:∵四边形是菱形,
∴,
∴,
∵,,
∴,
∴;
(2)解:∵四边形是菱形,,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴的长是.
【知识点】菱形的性质;相似三角形的判定-AA;相似三角形的性质-对应边
18.【答案】解:∵
∴
∴
∴
∴
∴
∴AE的长为5.
【知识点】相似三角形的判定-AA;相似三角形的性质-对应边
19.【答案】解:相似,
∵,,,
即,
∴这两个三角形相似.
【知识点】相似三角形的判定
20.【答案】(1)解:由∠DAB=∠EAC,得∠DAE=∠BAC.
∵∠ADE=∠ABC,
∴△ADE∽△ABC.
(2)解:∵△ADE∽△ABC,
∴,即
∵∠DAB=∠EAC,
∴△ADB∽△AEC.
【知识点】相似三角形的判定
21.【答案】(1);
(2)解:如图所示:
四边形是矩形,
,,
,
≌(AAS),
,,
设,则,
,
,
,
,
当点与点重合时,则,
,
要使绿化改造所需费用最少,则需满足矩形的面积最大,
当时,矩形的面积最大,最大值为,如图,
,
过点作于点,
,
,
,
,
,
四边形的面积为,
种植花卉的面积为,
所需费用最少为元;
答:绿化改造所需费用至少为元.
【知识点】三角形的面积;三角形全等及其性质;勾股定理;正方形的性质;相似三角形的判定
21世纪教育网(www.21cnjy.com)
2 / 10
5 相似三角形判定定理的证明
一、单选题
1.(2024九上·杭州月考)如图,下列条件不能判定的是( )
A. B.
C. D.
2.(2024九上·荔城期末)如图,在中,为上一点,若,则( )
A.~ B.~
C.~ D.无法判断
3.(2021九上·滨海月考)下列命题中,错误的是( )
A.所有的正多边形都相似
B.有一对锐角相等的两个直角三角形相似
C.全等的三角形一定相似
D.所有的等边三角形都相似
4.(2023九上·东昌府月考)如图,在中,点D、E分别在边上,与边不平行,那么下列条件中,能判定是( )
A. B.
C. D.
5.(2024九下·浦北月考)如图,下列条件不能判定的是( )
A. B. C. D.
6.(2024·呼和浩特)如图,在△ABD中,∠ABD=30°,∠A=105°,将△ABD沿BD翻折180°得到△CBD,将线段DC绕点D顺时针旋转30°得到线段DF,点E为AB的中点,连接EF,ED.若EF=1,则△BED的面积是( )
A. B. C. D.
7.(2019九上·南关期中)如图,在 中, ,将 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B.
C. D.
8.(2016九上·蓬江期末)如图,点P是 ABCD边AB上的一点,射线CP交DA的延长线于点E,则图中相似的三角形有( )
A.0对 B.1对 C.2对 D.3对
9.如图,△ABC中,∠C=90°,CD⊥AB,DE⊥AC,则图中与△ABC相似的三角形有( )
A.1个 B.2个 C.3个 D.4个
10.(2024九下·温州模拟)如图,正方形ABCD和正方形CGFE的顶点C,D,E在同一条直线上,顶点B,C,G在同一条直线上.O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接FH交EG于点M,连接OH.以下四个结论:①GH⊥BE;②△EHM∽△GHF;③﹣1;④=2﹣,其中正确的结论是( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题
11.(2023·金华模拟)如图,点P在△ABC的边AC上,请添加一个条件 ,使△ABP∽△ACB,
12.(2024九上·杭州期中)如图,、交于点,连接、,若要使,可以添加条件 .(只需写出一个条件即可)
13.(2023九上·鄞州月考)如图,已知,请添加一个条件 (只需填写一个即可),使得.
14.(2016九上·北京期中)如图,∠DAB=∠CAE,要使△ABC∽△ADE,则补充的一个条件可以是 (注:只需写出一个正确答案即可).
15.如图,在矩形ABCD中,AB= 4,AD= 8,点E,F分别在边AD,BC上,且AE= 3,按以下步骤操作:
第一步,沿直线EF翻折,点A的对应点A' 恰好落在对角线AC上,点B的对应点为B' ,则线段BF的长为 ;
第二步,分别在EF,AB' '上取点M,N,沿直线MN继续翻折,使点F与点E重合,则线段MN的长为 .
16.(2025九下·江海模拟)如图是一张矩形纸片,点是中点,点在上,把该纸片沿折叠,点的对应点分别为,的延长线经过点,与相交于点.若,且点平分,则的长为 .
三、计算题
17.(2024九上·苏州期末)如图,在菱形中,过D作交的延长线于点E,过E作交于点F.
(1)求证;
(2)若,求的长.
四、解答题
18.(2024九上·定州期末)如图,在△ABC中,AB=10,AC=8,点D,E分别是边AB、AC上的点,且AD=4,∠BDE+∠C=180°,求AE的长.
19.已知一个三角形三边的长分别为6cm,9cm,7.5cm,另一个三角形三边的长分别为8cm,10cm,12cm.试判断这两个三角形是否相似,并说明理由.
20.已知:如图,∠DAB=∠EAC,∠ADE=∠ABC.求证:
(1)△ADE∽△ABC.
(2)△ADB∽△AEC.
21.(2025九下·南山期中)问题提出
(1)如图,在中,,的面积为在内作一个正方形,使正方形一边落在边上,另外两个顶点,分别落在边,上,该正方形的面积大小为 ▲ .
问题解决
(2)某市进行绿化改造,美化生态环境如图,现有一块四边形的空地计划改造成公园,经测量,,,,且按设计要求,要在四边形公园内建造一个矩形活动场所,顶点,均在边上,顶点,分别在边,上为了满足居民需求,计划在矩形活动场所中种植草坪,在公园内其他区域种植花卉已知花卉每平方米元,草坪每平方米元,则绿化改造所需费用至少为多少元?结果保留整数,参考数据
答案解析部分
1.【答案】C
【知识点】相似三角形的判定
2.【答案】C
【知识点】相似三角形的判定
3.【答案】A
【知识点】相似多边形;相似三角形的判定
4.【答案】C
【知识点】相似三角形的判定
5.【答案】D
【知识点】相似三角形的判定
6.【答案】A
【知识点】三角形的面积;相似三角形的判定;三角形全等的判定-SAS
7.【答案】D
【知识点】相似三角形的判定
8.【答案】D
【知识点】平行四边形的性质;相似三角形的判定
9.【答案】D
【知识点】相似三角形的判定
10.【答案】A
【知识点】三角形全等及其性质;正方形的判定与性质;三角形全等的判定-SAS;相似三角形的判定-AA;相似三角形的性质-对应边
11.【答案】∠C=∠ABP(答案不唯一)
【知识点】相似三角形的判定
12.【答案】(答案不唯一)
【知识点】相似三角形的判定
13.【答案】或或(其中任何一个条件即可)
【知识点】相似三角形的判定
14.【答案】∠B=∠D
【知识点】相似三角形的判定
15.【答案】1;
【知识点】勾股定理;矩形的性质;翻折变换(折叠问题);相似三角形的判定;相似三角形的性质-对应边
16.【答案】
【知识点】矩形的性质;翻折变换(折叠问题);相似三角形的判定-AA;相似三角形的性质-对应边
17.【答案】(1)证明:∵四边形是菱形,
∴,
∴,
∵,,
∴,
∴;
(2)解:∵四边形是菱形,,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴的长是.
【知识点】菱形的性质;相似三角形的判定-AA;相似三角形的性质-对应边
18.【答案】解:∵
∴
∴
∴
∴
∴
∴AE的长为5.
【知识点】相似三角形的判定-AA;相似三角形的性质-对应边
19.【答案】解:相似,
∵,,,
即,
∴这两个三角形相似.
【知识点】相似三角形的判定
20.【答案】(1)解:由∠DAB=∠EAC,得∠DAE=∠BAC.
∵∠ADE=∠ABC,
∴△ADE∽△ABC.
(2)解:∵△ADE∽△ABC,
∴,即
∵∠DAB=∠EAC,
∴△ADB∽△AEC.
【知识点】相似三角形的判定
21.【答案】(1);
(2)解:如图所示:
四边形是矩形,
,,
,
≌(AAS),
,,
设,则,
,
,
,
,
当点与点重合时,则,
,
要使绿化改造所需费用最少,则需满足矩形的面积最大,
当时,矩形的面积最大,最大值为,如图,
,
过点作于点,
,
,
,
,
,
四边形的面积为,
种植花卉的面积为,
所需费用最少为元;
答:绿化改造所需费用至少为元.
【知识点】三角形的面积;三角形全等及其性质;勾股定理;正方形的性质;相似三角形的判定
21世纪教育网(www.21cnjy.com)
2 / 10
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
