6.3 反比例函数的应用 同步练习(含答案)
文档属性
| 名称 | 6.3 反比例函数的应用 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 634.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-09 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
3 反比例函数的应用
一、单选题
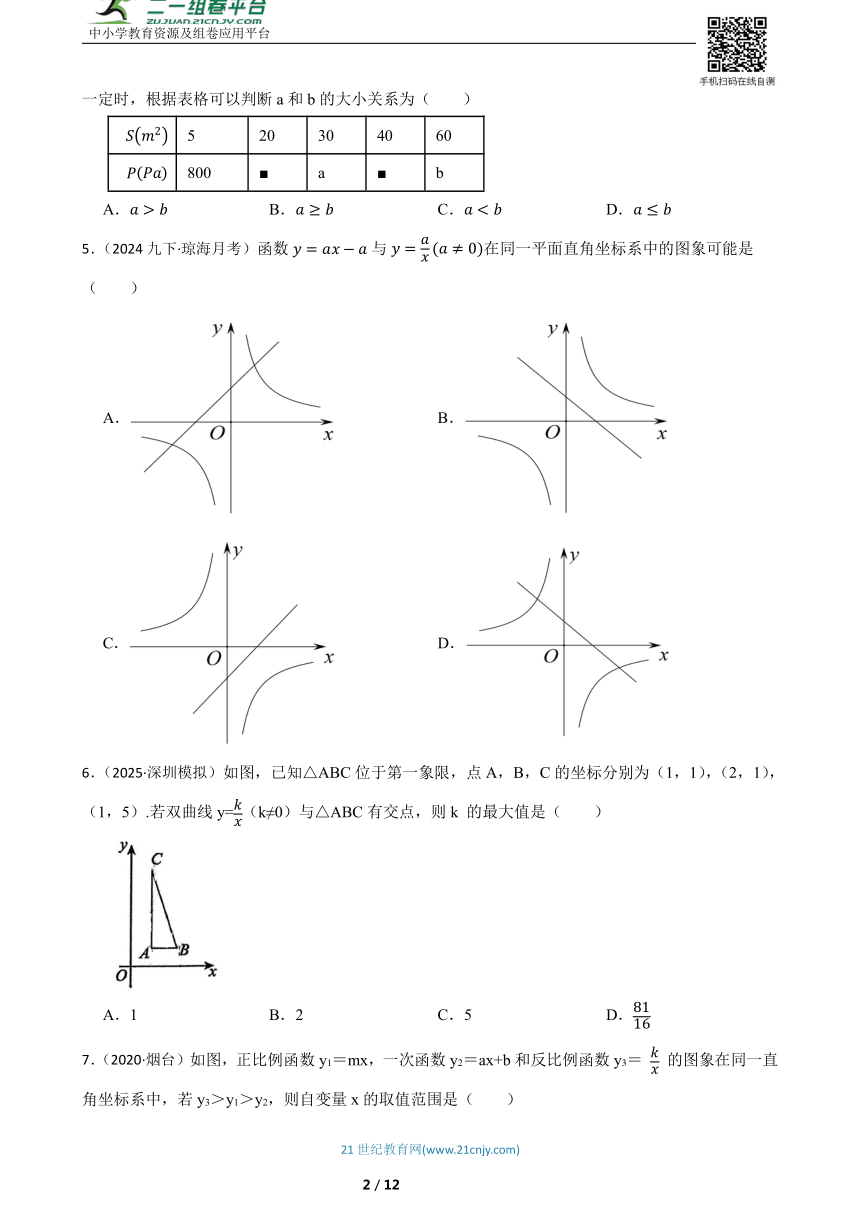
1.(2022九上·龙胜各族期中)矩形的面积一定,此矩形的长与宽的函数关系图象是( )
A. B.
C. D.
2.一辆汽车匀速通过某段公路, 所需时间 与行驶速度 满足函数关系 ,其图象为如图所示的一段曲线, 且端点为 和 . 若行驶速度不得超过 , 则汽车通过该段公路最少需要( )
A. B. C. D.
3.(2024九上·溆浦期中)已知关于x的函数和,它们在同一坐标系中的大致图象是( )
A. B.
C. D.
4.(2024·霍邱模拟)力F作用于物体,产生的压强p与物体受力面积S之间满足关系式,当F一定时,根据表格可以判断a和b的大小关系为( )
5 20 30 40 60
800 ■ a ■ b
A. B. C. D.
5.(2024九下·琼海月考)函数与在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
6.(2025·深圳模拟)如图,已知△ABC位于第一象限,点A,B,C的坐标分别为(1,1),(2,1),(1,5).若双曲线y=(k≠0)与△ABC有交点,则k 的最大值是( )
A.1 B.2 C.5 D.
7.(2020·烟台)如图,正比例函数y1=mx,一次函数y2=ax+b和反比例函数y3= 的图象在同一直角坐标系中,若y3>y1>y2,则自变量x的取值范围是( )
A.x<﹣1 B.﹣0.5<x<0或x>1
C.0<x<1 D.x<﹣1或0<x<1
8.若函数y= 与y=x+1的图象交于点A(a,b),则 的值为( )
A.- B. C.-3 D.3
9.已知广州市的土地总面积约为7434 km2,人均占有的土地面积S(单位:km2/人)随全市人口n(单位:人)的变化而变化,则S与n的函数关系式为( )
A.S=7434n B.S= C.n=7434S D.S=
10.(2025·凉州模拟)如图,直线与反比例函数相交于点,与轴交于点,将射线绕点逆时针旋转,交反比例函数图象于点,则点构成的三角形面积为( )
A. B. C. D.
二、填空题
11.(2024九上·常德期末)已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.若蓄电池电流为3A时,电阻为 Ω.
12.(2023九上·朝阳期中)近视眼镜的度数y(度)与镜片焦距x(m)成反比例(即),已知200度近视眼镜的镜片焦距为0.5m,则y与x之间的函数关系式是 .
13.(2025·桂阳模拟)中国古人用十二根长短不同的竹子做成律管,用它们分别吹出十二个标准音,称为十二律.十二律的音高由低到高排列依次是:黄钟、大吕、太簇、夹钟、姑洗、中吕、蕤宾、林钟、夷则、南吕、无射、应钟.律管越长,音高越低,古人采用“隔八相生法”、“三分损益法”确定每根律管长度:黄钟律管长九寸,减去三分之一,得到隔八音的林钟律管长六寸;林钟律管长减去三分之一,得到隔八音的清太簇律管长四寸,将长度翻倍,得到降八度对应的太簇律管长八寸,其余以此类推,可以得出每根律管长.这也对应了五音“宫生微、微生商、商生羽、羽生角”的相生关系.律管频率与律管长成反比关系,若黄钟律管频率为,则姑洗律管频率为 .
14.(2024九下·河北模拟)在平面直角坐标系中,直线,经过点,且与坐标轴围成的三角形的面积是9,与曲线的图象G交于A,B两点.
(1)则直线的表达式为 ;
(2)横、纵坐标都是整数的点叫作整点.记图象G在点A、B之间的部分与线段AB围成的区域(不含边界)为W.则区域W内的整点的坐标是 .
15.(2020·龙沙模拟)如图,直线 与双曲线 交于 两点, 轴, 轴与 交于点 ,则 的面积的最小值是 .
16.(2021·福田模拟)如图,函数y=x与y= (k>0)的图象相交于A,B两点,P是反比例函数图象上任一点(不与A,B重合),连接PA,PB.对于△ABP,有如下性质:|∠PBA﹣∠PAB|恒为定值且等于90°.根据上述性质完成:若在图中,tan∠PAB= ,△PAB的面积S△PAB=12,则k= .
三、计算题
17.(2023九上·南县月考)如图,直线与双曲线相交于、两点.
(1)求直线和双曲线的解析式;
(2)观察图像,请直接写出不等式的解集.
18.(2024九下·济宁模拟)如图,一次函数的图像与反比例函数的图像交于点和点.
(1)求反比例函数的解析式;
(2)若,根据图像直接写出当时的取值范围;
(3)点在线段上,过点作轴的垂线,交函数的图像于点,若的面积为1,求点的坐标.
19.(2024九上·济南期末)如图,一次函数的图象与x轴交于点,与y轴交于点B,与反比例函数的图象交于点C,D.若,.
(1)求一次函数和反比例函数的表达式;
(2)求的面积.
四、解答题
20.(2024·广州模拟)如图,反比例函数和一次函数的图象相交于点和点,且点的横坐标为,点的纵坐标为.过点作轴于点,的面积为.
(1)求反比例函数和一次函数的表达式;
(2)直接写出不等式的解集.
21.(2024九下·天河模拟)一艘载满货物的轮船到达南沙港码头后开始卸货.平均卸货速度y(单位:吨/天)与卸货天数t是反比例函数关系,它的图象如图所示.
(1)求y与t之间的函数解析式;
(2)南沙港码头收到气象部门的紧急通知,在某海域形成新的台风,预计7天后影响码头卸货,因此要求船上的货物不超过5天卸载完毕,那么平均每天至少要卸载多少吨?
22.(2024九上·沅江期中)如图,在平面直角坐标系中,一次函数与反比例函数的图象交于点,两点.
(1)求反比例函数和一次函数的表达式;
(2)如果点P是y轴上一点,且的面积是5,求的长;
(3)当时,请直接写出x的取值范围.
23.(2024九上·上海市月考)如图,函数的图象过点和点B,过点A作轴,(C在A的下方),过点C作轴,与函数的图象交于点D,过点B作于点E,连接.
(1)求的面积;
(2)延长交于点F,当时,求的长;
(3)连接,取中点Q,以线段为较长直角边且Q为直角顶点作,使得与相似,求出点P的坐标.
答案解析部分
1.【答案】B
【知识点】反比例函数的实际应用
2.【答案】B
【知识点】反比例函数的实际应用
3.【答案】A
【知识点】反比例函数与一次函数的交点问题
4.【答案】A
【知识点】反比例函数的实际应用
5.【答案】D
【知识点】反比例函数与一次函数的交点问题
6.【答案】D
【知识点】待定系数法求一次函数解析式;反比例函数与一次函数的交点问题
7.【答案】D
【知识点】一次函数的图象;反比例函数与一次函数的交点问题;比较一次函数值的大小
8.【答案】A
【知识点】反比例函数与一次函数的交点问题
9.【答案】B
【知识点】列反比例函数关系式
10.【答案】D
【知识点】因式分解法解一元二次方程;反比例函数与一次函数的交点问题;三角形的面积;三角形全等的判定-AAS;等腰三角形的概念
11.【答案】12
【知识点】反比例函数的实际应用
12.【答案】
【知识点】反比例函数的实际应用
13.【答案】324
【知识点】反比例函数的实际应用
14.【答案】;
【知识点】待定系数法求一次函数解析式;反比例函数与一次函数的交点问题;一次函数图象与坐标轴交点问题
15.【答案】12
【知识点】一元二次方程的根与系数的关系(韦达定理);反比例函数与一次函数的交点问题
16.【答案】
【知识点】反比例函数与一次函数的交点问题;三角形的面积
17.【答案】(1),.
(2)或.
【知识点】反比例函数与一次函数的交点问题
18.【答案】(1)
(2)
(3)点的坐标为或
【知识点】因式分解法解一元二次方程;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题
19.【答案】(1)解:,
,
又,
,
.
,B两点在直线上,
,
解得,
一次函数的表达式为.
如图,过点C作于点E,
,
,
易知,
,
,
,,
,
,
点C在反比例函数的图象上,
,
反比例函数的表达式为.
(2)解:由(1)建立方程组,
解得或,
,
如图,过点D作轴于点F,则,
.
【知识点】待定系数法求一次函数解析式;反比例函数与一次函数的交点问题;相似三角形的判定;相似三角形的性质-对应边
20.【答案】(1)反比例函数解析式为:,一次函数解析式为:
(2)或
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题
21.【答案】(1)
(2)平均每天至少要卸载48吨.
【知识点】待定系数法求反比例函数解析式;反比例函数的实际应用
22.【答案】(1);
(2)或
(3)或
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题;一次函数的实际应用-几何问题
23.【答案】(1)
(2)
(3)或
【知识点】反比例函数与一次函数的交点问题;勾股定理;相似三角形的性质
21世纪教育网(www.21cnjy.com)
1 / 12
3 反比例函数的应用
一、单选题
1.(2022九上·龙胜各族期中)矩形的面积一定,此矩形的长与宽的函数关系图象是( )
A. B.
C. D.
2.一辆汽车匀速通过某段公路, 所需时间 与行驶速度 满足函数关系 ,其图象为如图所示的一段曲线, 且端点为 和 . 若行驶速度不得超过 , 则汽车通过该段公路最少需要( )
A. B. C. D.
3.(2024九上·溆浦期中)已知关于x的函数和,它们在同一坐标系中的大致图象是( )
A. B.
C. D.
4.(2024·霍邱模拟)力F作用于物体,产生的压强p与物体受力面积S之间满足关系式,当F一定时,根据表格可以判断a和b的大小关系为( )
5 20 30 40 60
800 ■ a ■ b
A. B. C. D.
5.(2024九下·琼海月考)函数与在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
6.(2025·深圳模拟)如图,已知△ABC位于第一象限,点A,B,C的坐标分别为(1,1),(2,1),(1,5).若双曲线y=(k≠0)与△ABC有交点,则k 的最大值是( )
A.1 B.2 C.5 D.
7.(2020·烟台)如图,正比例函数y1=mx,一次函数y2=ax+b和反比例函数y3= 的图象在同一直角坐标系中,若y3>y1>y2,则自变量x的取值范围是( )
A.x<﹣1 B.﹣0.5<x<0或x>1
C.0<x<1 D.x<﹣1或0<x<1
8.若函数y= 与y=x+1的图象交于点A(a,b),则 的值为( )
A.- B. C.-3 D.3
9.已知广州市的土地总面积约为7434 km2,人均占有的土地面积S(单位:km2/人)随全市人口n(单位:人)的变化而变化,则S与n的函数关系式为( )
A.S=7434n B.S= C.n=7434S D.S=
10.(2025·凉州模拟)如图,直线与反比例函数相交于点,与轴交于点,将射线绕点逆时针旋转,交反比例函数图象于点,则点构成的三角形面积为( )
A. B. C. D.
二、填空题
11.(2024九上·常德期末)已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.若蓄电池电流为3A时,电阻为 Ω.
12.(2023九上·朝阳期中)近视眼镜的度数y(度)与镜片焦距x(m)成反比例(即),已知200度近视眼镜的镜片焦距为0.5m,则y与x之间的函数关系式是 .
13.(2025·桂阳模拟)中国古人用十二根长短不同的竹子做成律管,用它们分别吹出十二个标准音,称为十二律.十二律的音高由低到高排列依次是:黄钟、大吕、太簇、夹钟、姑洗、中吕、蕤宾、林钟、夷则、南吕、无射、应钟.律管越长,音高越低,古人采用“隔八相生法”、“三分损益法”确定每根律管长度:黄钟律管长九寸,减去三分之一,得到隔八音的林钟律管长六寸;林钟律管长减去三分之一,得到隔八音的清太簇律管长四寸,将长度翻倍,得到降八度对应的太簇律管长八寸,其余以此类推,可以得出每根律管长.这也对应了五音“宫生微、微生商、商生羽、羽生角”的相生关系.律管频率与律管长成反比关系,若黄钟律管频率为,则姑洗律管频率为 .
14.(2024九下·河北模拟)在平面直角坐标系中,直线,经过点,且与坐标轴围成的三角形的面积是9,与曲线的图象G交于A,B两点.
(1)则直线的表达式为 ;
(2)横、纵坐标都是整数的点叫作整点.记图象G在点A、B之间的部分与线段AB围成的区域(不含边界)为W.则区域W内的整点的坐标是 .
15.(2020·龙沙模拟)如图,直线 与双曲线 交于 两点, 轴, 轴与 交于点 ,则 的面积的最小值是 .
16.(2021·福田模拟)如图,函数y=x与y= (k>0)的图象相交于A,B两点,P是反比例函数图象上任一点(不与A,B重合),连接PA,PB.对于△ABP,有如下性质:|∠PBA﹣∠PAB|恒为定值且等于90°.根据上述性质完成:若在图中,tan∠PAB= ,△PAB的面积S△PAB=12,则k= .
三、计算题
17.(2023九上·南县月考)如图,直线与双曲线相交于、两点.
(1)求直线和双曲线的解析式;
(2)观察图像,请直接写出不等式的解集.
18.(2024九下·济宁模拟)如图,一次函数的图像与反比例函数的图像交于点和点.
(1)求反比例函数的解析式;
(2)若,根据图像直接写出当时的取值范围;
(3)点在线段上,过点作轴的垂线,交函数的图像于点,若的面积为1,求点的坐标.
19.(2024九上·济南期末)如图,一次函数的图象与x轴交于点,与y轴交于点B,与反比例函数的图象交于点C,D.若,.
(1)求一次函数和反比例函数的表达式;
(2)求的面积.
四、解答题
20.(2024·广州模拟)如图,反比例函数和一次函数的图象相交于点和点,且点的横坐标为,点的纵坐标为.过点作轴于点,的面积为.
(1)求反比例函数和一次函数的表达式;
(2)直接写出不等式的解集.
21.(2024九下·天河模拟)一艘载满货物的轮船到达南沙港码头后开始卸货.平均卸货速度y(单位:吨/天)与卸货天数t是反比例函数关系,它的图象如图所示.
(1)求y与t之间的函数解析式;
(2)南沙港码头收到气象部门的紧急通知,在某海域形成新的台风,预计7天后影响码头卸货,因此要求船上的货物不超过5天卸载完毕,那么平均每天至少要卸载多少吨?
22.(2024九上·沅江期中)如图,在平面直角坐标系中,一次函数与反比例函数的图象交于点,两点.
(1)求反比例函数和一次函数的表达式;
(2)如果点P是y轴上一点,且的面积是5,求的长;
(3)当时,请直接写出x的取值范围.
23.(2024九上·上海市月考)如图,函数的图象过点和点B,过点A作轴,(C在A的下方),过点C作轴,与函数的图象交于点D,过点B作于点E,连接.
(1)求的面积;
(2)延长交于点F,当时,求的长;
(3)连接,取中点Q,以线段为较长直角边且Q为直角顶点作,使得与相似,求出点P的坐标.
答案解析部分
1.【答案】B
【知识点】反比例函数的实际应用
2.【答案】B
【知识点】反比例函数的实际应用
3.【答案】A
【知识点】反比例函数与一次函数的交点问题
4.【答案】A
【知识点】反比例函数的实际应用
5.【答案】D
【知识点】反比例函数与一次函数的交点问题
6.【答案】D
【知识点】待定系数法求一次函数解析式;反比例函数与一次函数的交点问题
7.【答案】D
【知识点】一次函数的图象;反比例函数与一次函数的交点问题;比较一次函数值的大小
8.【答案】A
【知识点】反比例函数与一次函数的交点问题
9.【答案】B
【知识点】列反比例函数关系式
10.【答案】D
【知识点】因式分解法解一元二次方程;反比例函数与一次函数的交点问题;三角形的面积;三角形全等的判定-AAS;等腰三角形的概念
11.【答案】12
【知识点】反比例函数的实际应用
12.【答案】
【知识点】反比例函数的实际应用
13.【答案】324
【知识点】反比例函数的实际应用
14.【答案】;
【知识点】待定系数法求一次函数解析式;反比例函数与一次函数的交点问题;一次函数图象与坐标轴交点问题
15.【答案】12
【知识点】一元二次方程的根与系数的关系(韦达定理);反比例函数与一次函数的交点问题
16.【答案】
【知识点】反比例函数与一次函数的交点问题;三角形的面积
17.【答案】(1),.
(2)或.
【知识点】反比例函数与一次函数的交点问题
18.【答案】(1)
(2)
(3)点的坐标为或
【知识点】因式分解法解一元二次方程;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题
19.【答案】(1)解:,
,
又,
,
.
,B两点在直线上,
,
解得,
一次函数的表达式为.
如图,过点C作于点E,
,
,
易知,
,
,
,,
,
,
点C在反比例函数的图象上,
,
反比例函数的表达式为.
(2)解:由(1)建立方程组,
解得或,
,
如图,过点D作轴于点F,则,
.
【知识点】待定系数法求一次函数解析式;反比例函数与一次函数的交点问题;相似三角形的判定;相似三角形的性质-对应边
20.【答案】(1)反比例函数解析式为:,一次函数解析式为:
(2)或
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题
21.【答案】(1)
(2)平均每天至少要卸载48吨.
【知识点】待定系数法求反比例函数解析式;反比例函数的实际应用
22.【答案】(1);
(2)或
(3)或
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题;一次函数的实际应用-几何问题
23.【答案】(1)
(2)
(3)或
【知识点】反比例函数与一次函数的交点问题;勾股定理;相似三角形的性质
21世纪教育网(www.21cnjy.com)
1 / 12
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
