【期末押题卷】广东省深圳市2025-2026学年五年级上学期期末模拟数学预测卷北师大版(含解析)
文档属性
| 名称 | 【期末押题卷】广东省深圳市2025-2026学年五年级上学期期末模拟数学预测卷北师大版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 539.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
广东省深圳市2025-2026学年五年级上学期期末模拟数学预测卷
一.选择题(共7小题,满分14分,每小题2分)
1.80.1÷7.9的商在图中的大致位置是( )
A.A B.B C.C D.D
2.一个盒子里有6颗红球、8颗白球、15颗黑球和4颗黄球,且大小相同,从盒中摸一个球,摸出( )的可能性最大。
A.红球 B.白球 C.黑球 D.黄球
3.(2分)有404盒牛奶,选哪种箱子能正好装完?( )
A.4盒/箱 B.6盒/箱 C.8盒/箱 D.10盒/箱
4.(2分)“洗洗手,擦干手,消毒之后举举手,健康握在我手中。”为了防止病从“手”入,妈妈准备买1瓶抑菌洗手液、3包卫生湿巾和2瓶免洗洗手液。她认为带60元就够了。她是这样估算的:17+6×3+12×2=59(元)。她的算法( )
抑菌洗手液:16.8元/瓶 卫生温巾:5.7元/包 免洗洗手液:11.9元/瓶
A.合理 B.不合理 C.不确定
5.(2分)如图是某种药说明书的一部分,这瓶药最多够患者服用( )天。
[规格]每粒0.5克 [用法用量]口服,一次2粒,一日3次 [包装]固体药用塑料瓶装,100粒
A.16 B.33 C.50
6.(2分)淘气和笑笑玩转盘游戏,你认为选( )转盘对双方都公平。
A. B. C.
7.(2分)如图所示,梯形的面积是26,甲的面积是丙的,甲的面积是5,丁的面积是( )
A.6 B.3 C.12 D.无法确定
二.填空题(共8小题,满分24分,每小题3分)
8.(3分)9.05公顷= 平方米
9.(3分)在下面的横线上填上“>”“<”或“=”符号。
1
0.32
6.3千米 千米
10.(3分)20220201031是实验小学一位同学的学籍号,编号时设定尾数用“1”表示男生,“2”表示女生。其中“2022”表示入学时间,“02”表示学校编码,“01”表示一班,“03”表示学号。那么学籍号是20190403272的同学的学号是 ,性别是 (填“男”或“女”)。
11.(3分)里面有 个;7个是 ;1里面有 个。
12.(3分)笑笑清理储钱罐时,发现里面只有1元和5角的硬币,一共36枚,共26元,1元的硬币有 枚,5角的硬币有 枚。
13.(3分)一张纸条长36厘米,从左起先每隔3厘米点一个点,再从左起每隔4厘米点一个点,纸条的两端都不点,最后纸条上一共有 个点。
14.(3分)一支笔的售价是4.9元,王老师买198支笔,他带1000元 。(够或不够)
15.(3分)……按这样的规律摆下去,摆9个正六边形需要 根小棒。
三.计算题(共2小题,满分17分)
16.(12分)用简便方法计算。
0.72×99
10.5×28.3+10.5×71.7
29.6÷0.4÷2.5
17.(5分)计算如图中阴影部分的面积。(单位:米)
四.操作题(共1小题,满分6分)
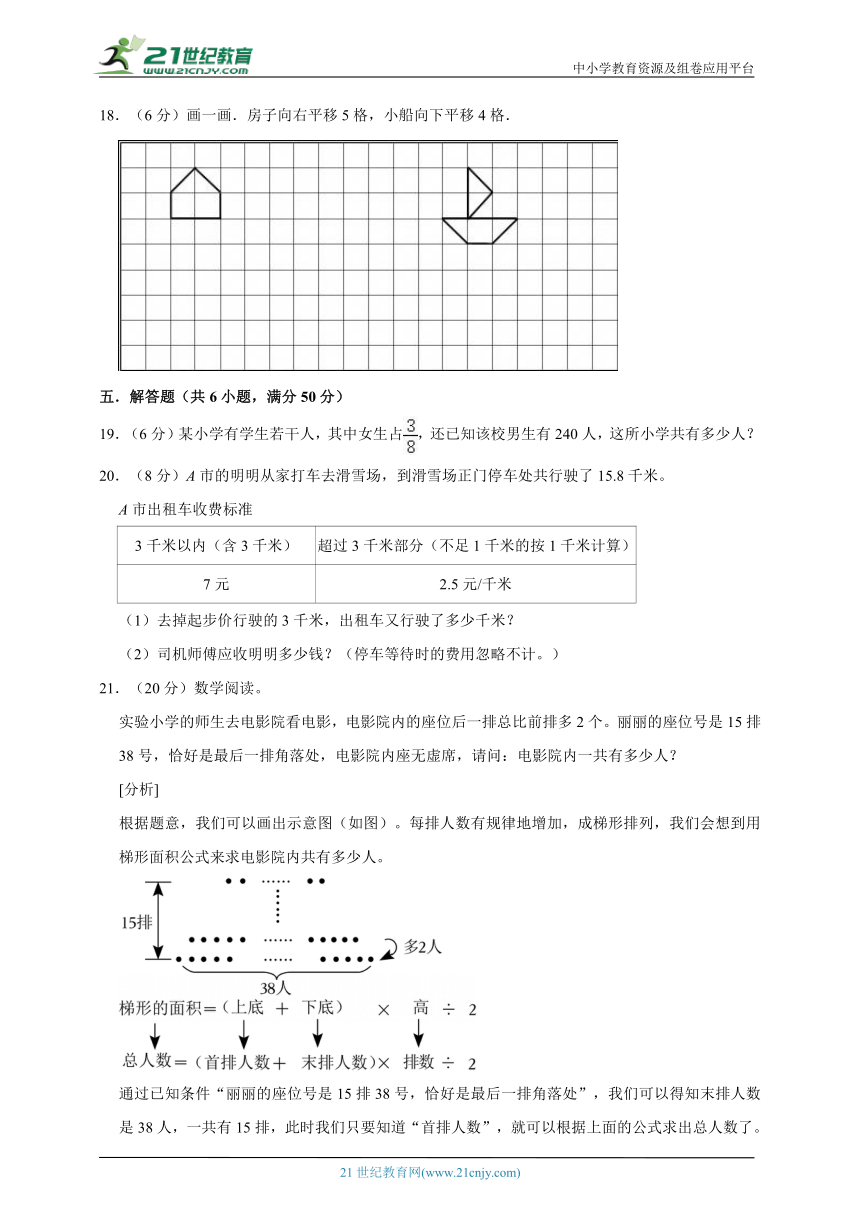
18.(6分)画一画.房子向右平移5格,小船向下平移4格.
五.解答题(共6小题,满分50分)
19.(6分)某小学有学生若干人,其中女生占,还已知该校男生有240人,这所小学共有多少人?
20.(8分)A市的明明从家打车去滑雪场,到滑雪场正门停车处共行驶了15.8千米。
A市出租车收费标准
3千米以内(含3千米) 超过3千米部分(不足1千米的按1千米计算)
7元 2.5元/千米
(1)去掉起步价行驶的3千米,出租车又行驶了多少千米?
(2)司机师傅应收明明多少钱?(停车等待时的费用忽略不计。)
21.(20分)数学阅读。
实验小学的师生去电影院看电影,电影院内的座位后一排总比前排多2个。丽丽的座位号是15排38号,恰好是最后一排角落处,电影院内座无虚席,请问:电影院内一共有多少人?
[分析]
根据题意,我们可以画出示意图(如图)。每排人数有规律地增加,成梯形排列,我们会想到用梯形面积公式来求电影院内共有多少人。
通过已知条件“丽丽的座位号是15排38号,恰好是最后一排角落处”,我们可以得知末排人数是38人,一共有15排,此时我们只要知道“首排人数”,就可以根据上面的公式求出总人数了。
(1)根据“后一排总比前一排多2个座位”和“第15排是38人”,可求出首排人数,我们可以这样解答:
(2)此时,我们已经知道首排人数、末排人数、排数,然后根据梯形的面积公式求出总人数,我们可以这样解答:
22.(5分)如图1,销售人员:我要推销一种新品单车,每购买一辆就能参加一次抽奖活动,并设立一、二、三等奖,人人有奖!请帮我设计一个方案吧!
小明:假设有10辆单车,应该设立一、二、三等奖各多少名才比较合理?
小美:奖品的总价不能超过10辆单车的盈利总额,才能保证让商家不亏本。
小刚:我想到可以使用“转盘”“翻扑克牌”“摸彩球”等很多方法来抽奖。
小丽:不管选择什么道具,都需要根据各奖项的人数,合理设计抽奖规则。
我的方案
(1)奖项设计。
奖项 奖项数量/个 奖品单价/元 奖品总价/元
一等奖
二等奖
三等奖
(2)抽奖设计。
道具介绍:转盘□扑克牌□彩球□(用打“√”的方式选择)
抽奖规则:(若选择“转盘”道具,可使用如图2表示规则)
广东省深圳市2025-2026学年五年级上学期期末模拟数学预测卷
参考答案与试题解析
一.选择题(共5小题,满分14分,每小题2分)
1.80.1÷7.9的商在图中的大致位置是( )
A.A B.B C.C D.D
【考点】小数除法;小数除法的近似数;数的估算.
【专题】整数的认识;数据分析观念.
【答案】B
【分析】把算式中的小数看作与它相近的整数,据此计算找出商所在的位置即可。
【解答】解:80.1÷7.9
≈80÷8
=10
因为把80.1估小了,7.9估大了,所以商比10大一些,A表示比10小,B表示比10大一些,C表示比10大很多,B点合适。
故选:B。
【点评】本题考查了小数除法的估算方法。
2.一个盒子里有6颗红球、8颗白球、15颗黑球和4颗黄球,且大小相同,从盒中摸一个球,摸出( )的可能性最大。
A.红球 B.白球 C.黑球 D.黄球
【考点】可能性的大小.
【专题】可能性;应用意识.
【答案】C
【分析】根据不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。据此解答即可。
【解答】解:15>8>6>4
所以从盒中摸一个球,摸出黑球的可能性最大。
故选:C。
【点评】解答此题的关键:应明确可能性的计算方法,并能根据实际情况进行灵活运用。
3.(2分)有404盒牛奶,选哪种箱子能正好装完?( )
A.4盒/箱 B.6盒/箱 C.8盒/箱 D.10盒/箱
【考点】整除的性质及应用.
【专题】数的整除;运算能力;应用意识.
【答案】A
【分析】根据整除的性质,404能被下面哪个数整除就选择哪一个。据此解答。
【解答】解:404÷4=101
406÷6=67…2
404÷8=50…4
404÷10=40…4
因为404是4的倍数,所以每箱4盒能正好装完。
故选:A。
【点评】此题考查的目的是理解掌握整除的性质及应用。
4.(2分)“洗洗手,擦干手,消毒之后举举手,健康握在我手中。”为了防止病从“手”入,妈妈准备买1瓶抑菌洗手液、3包卫生湿巾和2瓶免洗洗手液。她认为带60元就够了。她是这样估算的:17+6×3+12×2=59(元)。她的算法( )
抑菌洗手液:16.8元/瓶 卫生温巾:5.7元/包 免洗洗手液:11.9元/瓶
A.合理 B.不合理 C.不确定
【考点】整数、小数复合应用题.
【专题】应用题;应用意识.
【答案】A
【分析】根据题意,抑菌洗手液:16.8元/瓶,卫生温巾:5.7元/包,免洗洗手液:11.9元/瓶,所以求出几种产品大约的单价,然后乘数量,求出买这几种物品大约需要多少钱,再与带的钱比较,据此解答。
【解答】解:16.8≈17,5.7≈6,11.9≈12,
买1瓶抑菌洗手液、3包卫生湿巾和2瓶免洗洗手液大约花费:
17×1+3×6+12×2
=17+18+24
=59(元)
59元<60元
答:她的算法正确。
故选:A。
【点评】本题考查了整数、小数的复合应用题,解决本题的关键是求出每件产品价钱的约数。
5.(2分)如图是某种药说明书的一部分,这瓶药最多够患者服用( )天。
[规格]每粒0.5克 [用法用量]口服,一次2粒,一日3次 [包装]固体药用塑料瓶装,100粒
A.16 B.33 C.50
【考点】整数、小数复合应用题.
【专题】应用题;应用意识.
【答案】A
【分析】用一次口服的粒数乘一日吃的次数,求出一天需要吃的粒数,用总粒数除以一天吃的粒数,即可求出这瓶药够患者服用多少天。
【解答】解:2×3=6(粒)
100÷6=16(天)......4(粒)
答:这瓶药最多够患者服用16天。
故选:A。
【点评】本题考查一位数除两位数的计算及应用。理解题意,找出数量关系,列式计算即可。
6.(2分)淘气和笑笑玩转盘游戏,你认为选( )转盘对双方都公平。
A. B. C.
【考点】游戏规则的公平性.
【专题】综合判断题;推理能力.
【答案】B
【分析】指针停在黑色区域和白色区域的可能性相同,则游戏公平,据此选择。
【解答】解:游戏规则的公平性体现在参与游戏的任何一方的获胜可能性大小一致,即指针停下后停在黑色区域和白色区域的可能性一样,所以要求转盘中黑色和白色区域在转盘中的面积大小一样,只有B选项符合题意。
故选:B。
【点评】此题考查可能性的大小,根据日常生活经验判断。
7.(2分)如图所示,梯形的面积是26,甲的面积是丙的,甲的面积是5,丁的面积是( )
A.6 B.3 C.12 D.无法确定
【考点】梯形的面积.
【专题】几何直观;推理能力;应用意识.
【答案】A
【分析】首先把丙的面积看作单位“1”,甲的面积是丙的,那么丙的面积是甲面积的2倍,据此可以求出丙的面积,因为甲的面积+丁的面积=乙的面积+丁的面积,所以甲的面积等于乙的面积,然后根据减法的意义,用梯形的面积减去甲、乙、丙的面积就是丁的面积。
【解答】解:26﹣5﹣5﹣5÷
=16﹣10
=6
答:丁的面积是6。
故选:A。
【点评】此题考查的目的是理解掌握等底等底高的三角形的面积,掌握整数乘法减法的计算法则及应用。
二.填空题(共8小题,满分24分,每小题3分)
8.(3分)9.05公顷= 90500 平方米
【考点】大面积单位间的进率及单位换算.
【专题】长度、面积、体积单位;数感.
【答案】90500。
【分析】高级单位公顷化低级单位平方米乘进率10000。
【解答】解:9.05公顷=90500平方米
故答案为:90500。
【点评】本题是考查面积的单位换算。单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率。
9.(3分)在下面的横线上填上“>”“<”或“=”符号。
> 1
= 0.32
6.3千米 < 千米
【考点】分数大小的比较.
【专题】数感;运算能力.
【答案】>;=;<。
【分析】分数和小数比较:可以将分数化为小数,再按照小数比较大小的方法进行比较;整数和假分数比较:先把假分数化为带分数,再进行比较。据此解答。
【解答】解:因为=
>1
所以>1;
=0.32;
因为=6.33333……
所以6.3千米<千米。
故答案为:>;=;<。
【点评】本题主要考查了分数、小数大小比较的方法,要熟练掌握。
10.(3分)20220201031是实验小学一位同学的学籍号,编号时设定尾数用“1”表示男生,“2”表示女生。其中“2022”表示入学时间,“02”表示学校编码,“01”表示一班,“03”表示学号。那么学籍号是20190403272的同学的学号是 27 ,性别是 女 (填“男”或“女”)。
【考点】数字编码.
【专题】推理能力.
【答案】27,女。
【分析】根据题意,编号时设定尾数用“1”表示男生,“2”表示女生。其中“2022”表示入学时间,“02”表示学校编码,“01”表示一班,“03”表示学号,据此分析学籍号是20190403272的同学的学号和性别即可。
【解答】解:学籍号是20190403272的同学的学号是27,性别是女。
故答案为:27,女。
【点评】这类问题先根据给出编码找出每位上数字代表的含义,再根据这个含义编号码,解答即可。
11.(3分)里面有 3 个;7个是 ;1里面有 7 个。
【考点】分数的意义和读写.
【专题】综合填空题;数据分析观念.
【答案】见试题解答内容
【分析】分数单位是把单位“1”平均分成若干份,表示其中的一份的数;看看分数里面有多少个分数单位,据此解答。
【解答】解:里面有3个;7个是;1里面有7个。
故答案为:3;;7。
【点评】此题考查了分数的意义,要求学生掌握。
12.(3分)笑笑清理储钱罐时,发现里面只有1元和5角的硬币,一共36枚,共26元,1元的硬币有 16 枚,5角的硬币有 20 枚。
【考点】鸡兔同笼.
【专题】压轴题;应用意识.
【答案】16;20。
【分析】假设36枚硬币全是1元的,则一共有36元,这比已知的26元多了36﹣26=10(元),因为一枚1元的比一枚5角的多0.5元,所以5角的一共有10÷0.5=20(枚),然后进一步解答即可。
【解答】解:5角=0.5元
(1×36﹣26)÷(1﹣0.5)
=10÷0.5
=20(枚)
36﹣20=16(枚)
答:1元硬币有16枚、5角硬币有20枚。
故答案为:16;20。
【点评】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
13.(3分)一张纸条长36厘米,从左起先每隔3厘米点一个点,再从左起每隔4厘米点一个点,纸条的两端都不点,最后纸条上一共有 17 个点。
【考点】公因数和公倍数应用题.
【专题】约数倍数应用题;应用意识.
【答案】17。
【分析】每隔3厘米点一个点,一共可点:36÷3=12(个)
每隔4厘米点一个点,一共可点:36÷4=9(个)
因为3和4在36以内的公倍数为:12,24,36,所以在纸条上12cm和24cm处的点重合了,那么只能算一个,因为纸条的两端都不点,在36cm处的两个点都要去掉;根据植树问题模型,把总点数减去这些重合和不能算的点即可。
【解答】解:由分析可知:
36÷3=12(个)
36÷4=9(个)
12+9﹣1﹣1﹣2
=21﹣4
=17(个)
答:最后纸条上一共有17个点。
故答案为:17。
【点评】本题考查植树问题模型和公倍数的灵活运用,学生需熟练掌握如何找两个数的公倍数。
14.(3分)一支笔的售价是4.9元,王老师买198支笔,他带1000元 够 。(够或不够)
【考点】整数、小数复合应用题.
【专题】运算能力;应用意识.
【答案】够。
【分析】根据题意,用4.9乘198,求出买198支笔的钱数,然后再与1000元进行比较解答。
【解答】解:4.9×198=970.2(元)
970.2<1000
答:他带1000元够。
故答案为:够。
【点评】本题关键是根据整数乘法的意义,求出买198支笔的钱数,然后再比较解答。
15.(3分)……按这样的规律摆下去,摆9个正六边形需要 46 根小棒。
【考点】数与形结合的规律.
【专题】综合填空题;推理能力.
【答案】46。
【分析】观察图形发现:第一个图形需要6根小棒,多一个六边形,多用5根小棒,则第n个图形中,需要火柴6+5(n﹣1)=5n+1,据此计算。
【解答】解:观察图形发现:第一个图形需要6根小棒,多一个六边形,多用5根小棒,则第n个图形中,需要火柴6+5(n﹣1)=5n+1。
当n=9时,5n+1=5×9+1=46(根)
答:摆9个正六边形需要46根小棒。
故答案为:46。
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
三.计算题(共2小题,满分17分)
16.(12分)用简便方法计算。
0.72×99
10.5×28.3+10.5×71.7
29.6÷0.4÷2.5
【考点】运算定律与简便运算;小数乘法(推广整数乘法运算定律).
【专题】运算能力.
【答案】71.28;1050;29.6。
【分析】0.72×99,将99拆成(100﹣1),利用乘法分配律进行简算;
10.5×28.3+10.5×71.7,利用乘法分配律进行简算;
29.6÷0.4÷2.5,根据除法的性质,将后两个数先乘起来再计算。
【解答】解:0.72×99
=0.72×(100﹣1)
=0.72×100﹣0.72
=72﹣0.72
=71.28
10.5×28.3+10.5×71.7
=10.5×(28.3+71.7)
=10.5×100
=1050
29.6÷0.4÷2.5
=29.6÷(0.4×2.5)
=29.6÷1
=29.6
【点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
17.(5分)计算如图中阴影部分的面积。(单位:米)
【考点】组合图形的面积.
【专题】应用意识.
【答案】37平方米。
【分析】图中意义部分的面积等于边长为8米的正方形与边长为5米的正方形的面积和减去底为(8+5)米、高为8米的三角形的面积,根据“正方形的面积=边长×边长”“三角形的面积=底×高÷2”解答即可。
【解答】解:8×8+5×5﹣(8+5)×8÷2
=64+25﹣13×4
=89﹣52
=37(平方米)
【点评】把求阴影部分的面积转化为正方形的面积和与三角形的面积差是解题的关键。
四.操作题
18.(6分)画一画.房子向右平移5格,小船向下平移4格.
【考点】作平移后的图形.
【专题】作图题.
【答案】见试题解答内容
【分析】根据平移图形的特征,把小房子的各顶点分别向右平移5格,再依次连接各点即可得到房子向右平移5格后的图形;同理,把小船的各顶点分别向下平移4格,再依次连接各点即可得到小船向下平移4格后的图形.
【解答】解:画一画.房子向右平移5格,小船向下平移4格.
【点评】平移作图要注意:①方向;②距离.整个平移作图,就是把整个图案的每一个特征点按一定方向和一定的距离平行移动.
五.解答题(共6小题,满分50分)
19.(6分)某小学有学生若干人,其中女生占,还已知该校男生有240人,这所小学共有多少人?
【考点】分数除法应用题.
【专题】应用题;分数百分数应用题;应用意识.
【答案】见试题解答内容
【分析】把全校的总人数看成单位“1”,其中女生占,则男生人数占全校的1﹣,已知男生有240人,根据分数除法的意义即可解答.
【解答】解:240÷(1﹣)
=240÷
=384(人)
答:这所小学共有384人.
【点评】本题先找出单位“1”,已知一个数的几分之几是多少,求这个数用除法求解.
20.(8分)A市的明明从家打车去滑雪场,到滑雪场正门停车处共行驶了15.8千米。
A市出租车收费标准
3千米以内(含3千米) 超过3千米部分(不足1千米的按1千米计算)
7元 2.5元/千米
(1)去掉起步价行驶的3千米,出租车又行驶了多少千米?
(2)司机师傅应收明明多少钱?(停车等待时的费用忽略不计。)
【考点】整数、小数复合应用题.
【专题】简单应用题和一般复合应用题;应用意识.
【答案】(1)12.8千米;(2)39.5元。
【分析】(1)用车子行驶的总路程减去起步价行驶的路程即可求出出租车又行驶的路程。
(2)首先求出超过3千米的路程需要的钱数,再加上起步价即可解答。
【解答】解:(1)15.8﹣3=12.8(千米)
答:出租车又行驶了12.8千米。
(2)15.8千米看作16千米。
(16﹣3)×2.5+7
=13×2.5+7
=32.5+7
=39.5(元)
答:司机师傅应收明明39.5元。
【点评】本题考查小数复合应用题。解答时要弄清楚每段的临界点和每段的收费标准,再根据单价、数量、总价之间的关系列式计算。
21.(20分)数学阅读。
实验小学的师生去电影院看电影,电影院内的座位后一排总比前排多2个。丽丽的座位号是15排38号,恰好是最后一排角落处,电影院内座无虚席,请问:电影院内一共有多少人?
[分析]
根据题意,我们可以画出示意图(如图)。每排人数有规律地增加,成梯形排列,我们会想到用梯形面积公式来求电影院内共有多少人。
通过已知条件“丽丽的座位号是15排38号,恰好是最后一排角落处”,我们可以得知末排人数是38人,一共有15排,此时我们只要知道“首排人数”,就可以根据上面的公式求出总人数了。
(1)根据“后一排总比前一排多2个座位”和“第15排是38人”,可求出首排人数,我们可以这样解答:
(2)此时,我们已经知道首排人数、末排人数、排数,然后根据梯形的面积公式求出总人数,我们可以这样解答:
【考点】梯形的面积;数与形结合的规律.
【专题】空间观念;应用意识.
【答案】(1)10人;
(2)360人。
【分析】(1)第15排是38人,后一排总比前一排多2个座位,则第15排和首排的人数相差(15﹣1)×2人,则首排人数是38﹣(15﹣1)×2人。
(2)根据总人数=(用首排人数+末尾人数)×排数÷2,代入数据计算即可。
【解答】解:(1)38﹣(15﹣1)×2
=38﹣14×2
=38﹣28
=10(人)
答:首排人数是10人。
(2)(10+38)×15÷2
=48×15÷2
=720÷2
=360(人)
答:总人数是360人。
【点评】解决本题时应仔细读题,找出有用信息,根据题目给出的解题思路列式解答,关键是正确理解“后一排总比前一排多2个座位”,求出首排人数。
21.(5分)如图1,销售人员:我要推销一种新品单车,每购买一辆就能参加一次抽奖活动,并设立一、二、三等奖,人人有奖!请帮我设计一个方案吧!
小明:假设有10辆单车,应该设立一、二、三等奖各多少名才比较合理?
小美:奖品的总价不能超过10辆单车的盈利总额,才能保证让商家不亏本。
小刚:我想到可以使用“转盘”“翻扑克牌”“摸彩球”等很多方法来抽奖。
小丽:不管选择什么道具,都需要根据各奖项的人数,合理设计抽奖规则。
我的方案
(1)奖项设计。
奖项 奖项数量/个 奖品单价/元 奖品总价/元
一等奖
二等奖
三等奖
(2)抽奖设计。
道具介绍:转盘□扑克牌□彩球□(用打“√”的方式选择)
抽奖规则:(若选择“转盘”道具,可使用如图2表示规则)
【考点】游戏规则的公平性.
【专题】综合题;应用意识.
【答案】
奖项 奖项数量/个 奖品单价/元 奖品总价/元
一等奖 1 300 850
二等奖 2 100
三等奖 7 50
抽奖规则:盒子里面有3种颜色的10个彩球,其中红球1个,蓝球2个,绿球7个,摸到红球中一等奖,摸到蓝球中二等奖,摸到绿球中三等奖。
【分析】(1)根据利润=售卖价﹣进货价计算出10辆单车的盈利总额;然后设计合理的抽奖方案,既能让销售人员留有部分盈利金额还能带动消费;
(2)选择摸彩球的方式:盒子里面有3种颜色的10个彩球,其中红球1个,蓝球2个,绿球7个,摸到红球中一等奖,摸到蓝球中二等奖,摸到绿球中三等奖。据此设计即可。
【解答】解:(1)10×(780﹣650)=1300(元)
可以设计一等奖1个,奖品单价300元,二等奖2个,奖品单价100元,三等奖7个,奖品单价50元,则奖品总价为:
1×300+2×100+7×50
=300+200+350
=850(元)
850<1300,既能让销售人员留有部分盈利金额还能带动消费。
奖项设计如下:
奖项 奖项数量/个 奖品单价/元 奖品总价/元
一等奖 1 300 850
二等奖 2 100
三等奖 7 50
(2)选择摸彩球的方式:
抽奖规则:盒子里面有3种颜色的10个彩球,其中红球1个,蓝球2个,绿球7个,摸到红球中一等奖,摸到蓝球中二等奖,摸到绿球中三等奖。
故答案为:1;300;850;2;100;7;50。
【点评】本题考查了可能性大小及游戏规则的公平性的应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
广东省深圳市2025-2026学年五年级上学期期末模拟数学预测卷
一.选择题(共7小题,满分14分,每小题2分)
1.80.1÷7.9的商在图中的大致位置是( )
A.A B.B C.C D.D
2.一个盒子里有6颗红球、8颗白球、15颗黑球和4颗黄球,且大小相同,从盒中摸一个球,摸出( )的可能性最大。
A.红球 B.白球 C.黑球 D.黄球
3.(2分)有404盒牛奶,选哪种箱子能正好装完?( )
A.4盒/箱 B.6盒/箱 C.8盒/箱 D.10盒/箱
4.(2分)“洗洗手,擦干手,消毒之后举举手,健康握在我手中。”为了防止病从“手”入,妈妈准备买1瓶抑菌洗手液、3包卫生湿巾和2瓶免洗洗手液。她认为带60元就够了。她是这样估算的:17+6×3+12×2=59(元)。她的算法( )
抑菌洗手液:16.8元/瓶 卫生温巾:5.7元/包 免洗洗手液:11.9元/瓶
A.合理 B.不合理 C.不确定
5.(2分)如图是某种药说明书的一部分,这瓶药最多够患者服用( )天。
[规格]每粒0.5克 [用法用量]口服,一次2粒,一日3次 [包装]固体药用塑料瓶装,100粒
A.16 B.33 C.50
6.(2分)淘气和笑笑玩转盘游戏,你认为选( )转盘对双方都公平。
A. B. C.
7.(2分)如图所示,梯形的面积是26,甲的面积是丙的,甲的面积是5,丁的面积是( )
A.6 B.3 C.12 D.无法确定
二.填空题(共8小题,满分24分,每小题3分)
8.(3分)9.05公顷= 平方米
9.(3分)在下面的横线上填上“>”“<”或“=”符号。
1
0.32
6.3千米 千米
10.(3分)20220201031是实验小学一位同学的学籍号,编号时设定尾数用“1”表示男生,“2”表示女生。其中“2022”表示入学时间,“02”表示学校编码,“01”表示一班,“03”表示学号。那么学籍号是20190403272的同学的学号是 ,性别是 (填“男”或“女”)。
11.(3分)里面有 个;7个是 ;1里面有 个。
12.(3分)笑笑清理储钱罐时,发现里面只有1元和5角的硬币,一共36枚,共26元,1元的硬币有 枚,5角的硬币有 枚。
13.(3分)一张纸条长36厘米,从左起先每隔3厘米点一个点,再从左起每隔4厘米点一个点,纸条的两端都不点,最后纸条上一共有 个点。
14.(3分)一支笔的售价是4.9元,王老师买198支笔,他带1000元 。(够或不够)
15.(3分)……按这样的规律摆下去,摆9个正六边形需要 根小棒。
三.计算题(共2小题,满分17分)
16.(12分)用简便方法计算。
0.72×99
10.5×28.3+10.5×71.7
29.6÷0.4÷2.5
17.(5分)计算如图中阴影部分的面积。(单位:米)
四.操作题(共1小题,满分6分)
18.(6分)画一画.房子向右平移5格,小船向下平移4格.
五.解答题(共6小题,满分50分)
19.(6分)某小学有学生若干人,其中女生占,还已知该校男生有240人,这所小学共有多少人?
20.(8分)A市的明明从家打车去滑雪场,到滑雪场正门停车处共行驶了15.8千米。
A市出租车收费标准
3千米以内(含3千米) 超过3千米部分(不足1千米的按1千米计算)
7元 2.5元/千米
(1)去掉起步价行驶的3千米,出租车又行驶了多少千米?
(2)司机师傅应收明明多少钱?(停车等待时的费用忽略不计。)
21.(20分)数学阅读。
实验小学的师生去电影院看电影,电影院内的座位后一排总比前排多2个。丽丽的座位号是15排38号,恰好是最后一排角落处,电影院内座无虚席,请问:电影院内一共有多少人?
[分析]
根据题意,我们可以画出示意图(如图)。每排人数有规律地增加,成梯形排列,我们会想到用梯形面积公式来求电影院内共有多少人。
通过已知条件“丽丽的座位号是15排38号,恰好是最后一排角落处”,我们可以得知末排人数是38人,一共有15排,此时我们只要知道“首排人数”,就可以根据上面的公式求出总人数了。
(1)根据“后一排总比前一排多2个座位”和“第15排是38人”,可求出首排人数,我们可以这样解答:
(2)此时,我们已经知道首排人数、末排人数、排数,然后根据梯形的面积公式求出总人数,我们可以这样解答:
22.(5分)如图1,销售人员:我要推销一种新品单车,每购买一辆就能参加一次抽奖活动,并设立一、二、三等奖,人人有奖!请帮我设计一个方案吧!
小明:假设有10辆单车,应该设立一、二、三等奖各多少名才比较合理?
小美:奖品的总价不能超过10辆单车的盈利总额,才能保证让商家不亏本。
小刚:我想到可以使用“转盘”“翻扑克牌”“摸彩球”等很多方法来抽奖。
小丽:不管选择什么道具,都需要根据各奖项的人数,合理设计抽奖规则。
我的方案
(1)奖项设计。
奖项 奖项数量/个 奖品单价/元 奖品总价/元
一等奖
二等奖
三等奖
(2)抽奖设计。
道具介绍:转盘□扑克牌□彩球□(用打“√”的方式选择)
抽奖规则:(若选择“转盘”道具,可使用如图2表示规则)
广东省深圳市2025-2026学年五年级上学期期末模拟数学预测卷
参考答案与试题解析
一.选择题(共5小题,满分14分,每小题2分)
1.80.1÷7.9的商在图中的大致位置是( )
A.A B.B C.C D.D
【考点】小数除法;小数除法的近似数;数的估算.
【专题】整数的认识;数据分析观念.
【答案】B
【分析】把算式中的小数看作与它相近的整数,据此计算找出商所在的位置即可。
【解答】解:80.1÷7.9
≈80÷8
=10
因为把80.1估小了,7.9估大了,所以商比10大一些,A表示比10小,B表示比10大一些,C表示比10大很多,B点合适。
故选:B。
【点评】本题考查了小数除法的估算方法。
2.一个盒子里有6颗红球、8颗白球、15颗黑球和4颗黄球,且大小相同,从盒中摸一个球,摸出( )的可能性最大。
A.红球 B.白球 C.黑球 D.黄球
【考点】可能性的大小.
【专题】可能性;应用意识.
【答案】C
【分析】根据不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。据此解答即可。
【解答】解:15>8>6>4
所以从盒中摸一个球,摸出黑球的可能性最大。
故选:C。
【点评】解答此题的关键:应明确可能性的计算方法,并能根据实际情况进行灵活运用。
3.(2分)有404盒牛奶,选哪种箱子能正好装完?( )
A.4盒/箱 B.6盒/箱 C.8盒/箱 D.10盒/箱
【考点】整除的性质及应用.
【专题】数的整除;运算能力;应用意识.
【答案】A
【分析】根据整除的性质,404能被下面哪个数整除就选择哪一个。据此解答。
【解答】解:404÷4=101
406÷6=67…2
404÷8=50…4
404÷10=40…4
因为404是4的倍数,所以每箱4盒能正好装完。
故选:A。
【点评】此题考查的目的是理解掌握整除的性质及应用。
4.(2分)“洗洗手,擦干手,消毒之后举举手,健康握在我手中。”为了防止病从“手”入,妈妈准备买1瓶抑菌洗手液、3包卫生湿巾和2瓶免洗洗手液。她认为带60元就够了。她是这样估算的:17+6×3+12×2=59(元)。她的算法( )
抑菌洗手液:16.8元/瓶 卫生温巾:5.7元/包 免洗洗手液:11.9元/瓶
A.合理 B.不合理 C.不确定
【考点】整数、小数复合应用题.
【专题】应用题;应用意识.
【答案】A
【分析】根据题意,抑菌洗手液:16.8元/瓶,卫生温巾:5.7元/包,免洗洗手液:11.9元/瓶,所以求出几种产品大约的单价,然后乘数量,求出买这几种物品大约需要多少钱,再与带的钱比较,据此解答。
【解答】解:16.8≈17,5.7≈6,11.9≈12,
买1瓶抑菌洗手液、3包卫生湿巾和2瓶免洗洗手液大约花费:
17×1+3×6+12×2
=17+18+24
=59(元)
59元<60元
答:她的算法正确。
故选:A。
【点评】本题考查了整数、小数的复合应用题,解决本题的关键是求出每件产品价钱的约数。
5.(2分)如图是某种药说明书的一部分,这瓶药最多够患者服用( )天。
[规格]每粒0.5克 [用法用量]口服,一次2粒,一日3次 [包装]固体药用塑料瓶装,100粒
A.16 B.33 C.50
【考点】整数、小数复合应用题.
【专题】应用题;应用意识.
【答案】A
【分析】用一次口服的粒数乘一日吃的次数,求出一天需要吃的粒数,用总粒数除以一天吃的粒数,即可求出这瓶药够患者服用多少天。
【解答】解:2×3=6(粒)
100÷6=16(天)......4(粒)
答:这瓶药最多够患者服用16天。
故选:A。
【点评】本题考查一位数除两位数的计算及应用。理解题意,找出数量关系,列式计算即可。
6.(2分)淘气和笑笑玩转盘游戏,你认为选( )转盘对双方都公平。
A. B. C.
【考点】游戏规则的公平性.
【专题】综合判断题;推理能力.
【答案】B
【分析】指针停在黑色区域和白色区域的可能性相同,则游戏公平,据此选择。
【解答】解:游戏规则的公平性体现在参与游戏的任何一方的获胜可能性大小一致,即指针停下后停在黑色区域和白色区域的可能性一样,所以要求转盘中黑色和白色区域在转盘中的面积大小一样,只有B选项符合题意。
故选:B。
【点评】此题考查可能性的大小,根据日常生活经验判断。
7.(2分)如图所示,梯形的面积是26,甲的面积是丙的,甲的面积是5,丁的面积是( )
A.6 B.3 C.12 D.无法确定
【考点】梯形的面积.
【专题】几何直观;推理能力;应用意识.
【答案】A
【分析】首先把丙的面积看作单位“1”,甲的面积是丙的,那么丙的面积是甲面积的2倍,据此可以求出丙的面积,因为甲的面积+丁的面积=乙的面积+丁的面积,所以甲的面积等于乙的面积,然后根据减法的意义,用梯形的面积减去甲、乙、丙的面积就是丁的面积。
【解答】解:26﹣5﹣5﹣5÷
=16﹣10
=6
答:丁的面积是6。
故选:A。
【点评】此题考查的目的是理解掌握等底等底高的三角形的面积,掌握整数乘法减法的计算法则及应用。
二.填空题(共8小题,满分24分,每小题3分)
8.(3分)9.05公顷= 90500 平方米
【考点】大面积单位间的进率及单位换算.
【专题】长度、面积、体积单位;数感.
【答案】90500。
【分析】高级单位公顷化低级单位平方米乘进率10000。
【解答】解:9.05公顷=90500平方米
故答案为:90500。
【点评】本题是考查面积的单位换算。单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率。
9.(3分)在下面的横线上填上“>”“<”或“=”符号。
> 1
= 0.32
6.3千米 < 千米
【考点】分数大小的比较.
【专题】数感;运算能力.
【答案】>;=;<。
【分析】分数和小数比较:可以将分数化为小数,再按照小数比较大小的方法进行比较;整数和假分数比较:先把假分数化为带分数,再进行比较。据此解答。
【解答】解:因为=
>1
所以>1;
=0.32;
因为=6.33333……
所以6.3千米<千米。
故答案为:>;=;<。
【点评】本题主要考查了分数、小数大小比较的方法,要熟练掌握。
10.(3分)20220201031是实验小学一位同学的学籍号,编号时设定尾数用“1”表示男生,“2”表示女生。其中“2022”表示入学时间,“02”表示学校编码,“01”表示一班,“03”表示学号。那么学籍号是20190403272的同学的学号是 27 ,性别是 女 (填“男”或“女”)。
【考点】数字编码.
【专题】推理能力.
【答案】27,女。
【分析】根据题意,编号时设定尾数用“1”表示男生,“2”表示女生。其中“2022”表示入学时间,“02”表示学校编码,“01”表示一班,“03”表示学号,据此分析学籍号是20190403272的同学的学号和性别即可。
【解答】解:学籍号是20190403272的同学的学号是27,性别是女。
故答案为:27,女。
【点评】这类问题先根据给出编码找出每位上数字代表的含义,再根据这个含义编号码,解答即可。
11.(3分)里面有 3 个;7个是 ;1里面有 7 个。
【考点】分数的意义和读写.
【专题】综合填空题;数据分析观念.
【答案】见试题解答内容
【分析】分数单位是把单位“1”平均分成若干份,表示其中的一份的数;看看分数里面有多少个分数单位,据此解答。
【解答】解:里面有3个;7个是;1里面有7个。
故答案为:3;;7。
【点评】此题考查了分数的意义,要求学生掌握。
12.(3分)笑笑清理储钱罐时,发现里面只有1元和5角的硬币,一共36枚,共26元,1元的硬币有 16 枚,5角的硬币有 20 枚。
【考点】鸡兔同笼.
【专题】压轴题;应用意识.
【答案】16;20。
【分析】假设36枚硬币全是1元的,则一共有36元,这比已知的26元多了36﹣26=10(元),因为一枚1元的比一枚5角的多0.5元,所以5角的一共有10÷0.5=20(枚),然后进一步解答即可。
【解答】解:5角=0.5元
(1×36﹣26)÷(1﹣0.5)
=10÷0.5
=20(枚)
36﹣20=16(枚)
答:1元硬币有16枚、5角硬币有20枚。
故答案为:16;20。
【点评】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
13.(3分)一张纸条长36厘米,从左起先每隔3厘米点一个点,再从左起每隔4厘米点一个点,纸条的两端都不点,最后纸条上一共有 17 个点。
【考点】公因数和公倍数应用题.
【专题】约数倍数应用题;应用意识.
【答案】17。
【分析】每隔3厘米点一个点,一共可点:36÷3=12(个)
每隔4厘米点一个点,一共可点:36÷4=9(个)
因为3和4在36以内的公倍数为:12,24,36,所以在纸条上12cm和24cm处的点重合了,那么只能算一个,因为纸条的两端都不点,在36cm处的两个点都要去掉;根据植树问题模型,把总点数减去这些重合和不能算的点即可。
【解答】解:由分析可知:
36÷3=12(个)
36÷4=9(个)
12+9﹣1﹣1﹣2
=21﹣4
=17(个)
答:最后纸条上一共有17个点。
故答案为:17。
【点评】本题考查植树问题模型和公倍数的灵活运用,学生需熟练掌握如何找两个数的公倍数。
14.(3分)一支笔的售价是4.9元,王老师买198支笔,他带1000元 够 。(够或不够)
【考点】整数、小数复合应用题.
【专题】运算能力;应用意识.
【答案】够。
【分析】根据题意,用4.9乘198,求出买198支笔的钱数,然后再与1000元进行比较解答。
【解答】解:4.9×198=970.2(元)
970.2<1000
答:他带1000元够。
故答案为:够。
【点评】本题关键是根据整数乘法的意义,求出买198支笔的钱数,然后再比较解答。
15.(3分)……按这样的规律摆下去,摆9个正六边形需要 46 根小棒。
【考点】数与形结合的规律.
【专题】综合填空题;推理能力.
【答案】46。
【分析】观察图形发现:第一个图形需要6根小棒,多一个六边形,多用5根小棒,则第n个图形中,需要火柴6+5(n﹣1)=5n+1,据此计算。
【解答】解:观察图形发现:第一个图形需要6根小棒,多一个六边形,多用5根小棒,则第n个图形中,需要火柴6+5(n﹣1)=5n+1。
当n=9时,5n+1=5×9+1=46(根)
答:摆9个正六边形需要46根小棒。
故答案为:46。
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
三.计算题(共2小题,满分17分)
16.(12分)用简便方法计算。
0.72×99
10.5×28.3+10.5×71.7
29.6÷0.4÷2.5
【考点】运算定律与简便运算;小数乘法(推广整数乘法运算定律).
【专题】运算能力.
【答案】71.28;1050;29.6。
【分析】0.72×99,将99拆成(100﹣1),利用乘法分配律进行简算;
10.5×28.3+10.5×71.7,利用乘法分配律进行简算;
29.6÷0.4÷2.5,根据除法的性质,将后两个数先乘起来再计算。
【解答】解:0.72×99
=0.72×(100﹣1)
=0.72×100﹣0.72
=72﹣0.72
=71.28
10.5×28.3+10.5×71.7
=10.5×(28.3+71.7)
=10.5×100
=1050
29.6÷0.4÷2.5
=29.6÷(0.4×2.5)
=29.6÷1
=29.6
【点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
17.(5分)计算如图中阴影部分的面积。(单位:米)
【考点】组合图形的面积.
【专题】应用意识.
【答案】37平方米。
【分析】图中意义部分的面积等于边长为8米的正方形与边长为5米的正方形的面积和减去底为(8+5)米、高为8米的三角形的面积,根据“正方形的面积=边长×边长”“三角形的面积=底×高÷2”解答即可。
【解答】解:8×8+5×5﹣(8+5)×8÷2
=64+25﹣13×4
=89﹣52
=37(平方米)
【点评】把求阴影部分的面积转化为正方形的面积和与三角形的面积差是解题的关键。
四.操作题
18.(6分)画一画.房子向右平移5格,小船向下平移4格.
【考点】作平移后的图形.
【专题】作图题.
【答案】见试题解答内容
【分析】根据平移图形的特征,把小房子的各顶点分别向右平移5格,再依次连接各点即可得到房子向右平移5格后的图形;同理,把小船的各顶点分别向下平移4格,再依次连接各点即可得到小船向下平移4格后的图形.
【解答】解:画一画.房子向右平移5格,小船向下平移4格.
【点评】平移作图要注意:①方向;②距离.整个平移作图,就是把整个图案的每一个特征点按一定方向和一定的距离平行移动.
五.解答题(共6小题,满分50分)
19.(6分)某小学有学生若干人,其中女生占,还已知该校男生有240人,这所小学共有多少人?
【考点】分数除法应用题.
【专题】应用题;分数百分数应用题;应用意识.
【答案】见试题解答内容
【分析】把全校的总人数看成单位“1”,其中女生占,则男生人数占全校的1﹣,已知男生有240人,根据分数除法的意义即可解答.
【解答】解:240÷(1﹣)
=240÷
=384(人)
答:这所小学共有384人.
【点评】本题先找出单位“1”,已知一个数的几分之几是多少,求这个数用除法求解.
20.(8分)A市的明明从家打车去滑雪场,到滑雪场正门停车处共行驶了15.8千米。
A市出租车收费标准
3千米以内(含3千米) 超过3千米部分(不足1千米的按1千米计算)
7元 2.5元/千米
(1)去掉起步价行驶的3千米,出租车又行驶了多少千米?
(2)司机师傅应收明明多少钱?(停车等待时的费用忽略不计。)
【考点】整数、小数复合应用题.
【专题】简单应用题和一般复合应用题;应用意识.
【答案】(1)12.8千米;(2)39.5元。
【分析】(1)用车子行驶的总路程减去起步价行驶的路程即可求出出租车又行驶的路程。
(2)首先求出超过3千米的路程需要的钱数,再加上起步价即可解答。
【解答】解:(1)15.8﹣3=12.8(千米)
答:出租车又行驶了12.8千米。
(2)15.8千米看作16千米。
(16﹣3)×2.5+7
=13×2.5+7
=32.5+7
=39.5(元)
答:司机师傅应收明明39.5元。
【点评】本题考查小数复合应用题。解答时要弄清楚每段的临界点和每段的收费标准,再根据单价、数量、总价之间的关系列式计算。
21.(20分)数学阅读。
实验小学的师生去电影院看电影,电影院内的座位后一排总比前排多2个。丽丽的座位号是15排38号,恰好是最后一排角落处,电影院内座无虚席,请问:电影院内一共有多少人?
[分析]
根据题意,我们可以画出示意图(如图)。每排人数有规律地增加,成梯形排列,我们会想到用梯形面积公式来求电影院内共有多少人。
通过已知条件“丽丽的座位号是15排38号,恰好是最后一排角落处”,我们可以得知末排人数是38人,一共有15排,此时我们只要知道“首排人数”,就可以根据上面的公式求出总人数了。
(1)根据“后一排总比前一排多2个座位”和“第15排是38人”,可求出首排人数,我们可以这样解答:
(2)此时,我们已经知道首排人数、末排人数、排数,然后根据梯形的面积公式求出总人数,我们可以这样解答:
【考点】梯形的面积;数与形结合的规律.
【专题】空间观念;应用意识.
【答案】(1)10人;
(2)360人。
【分析】(1)第15排是38人,后一排总比前一排多2个座位,则第15排和首排的人数相差(15﹣1)×2人,则首排人数是38﹣(15﹣1)×2人。
(2)根据总人数=(用首排人数+末尾人数)×排数÷2,代入数据计算即可。
【解答】解:(1)38﹣(15﹣1)×2
=38﹣14×2
=38﹣28
=10(人)
答:首排人数是10人。
(2)(10+38)×15÷2
=48×15÷2
=720÷2
=360(人)
答:总人数是360人。
【点评】解决本题时应仔细读题,找出有用信息,根据题目给出的解题思路列式解答,关键是正确理解“后一排总比前一排多2个座位”,求出首排人数。
21.(5分)如图1,销售人员:我要推销一种新品单车,每购买一辆就能参加一次抽奖活动,并设立一、二、三等奖,人人有奖!请帮我设计一个方案吧!
小明:假设有10辆单车,应该设立一、二、三等奖各多少名才比较合理?
小美:奖品的总价不能超过10辆单车的盈利总额,才能保证让商家不亏本。
小刚:我想到可以使用“转盘”“翻扑克牌”“摸彩球”等很多方法来抽奖。
小丽:不管选择什么道具,都需要根据各奖项的人数,合理设计抽奖规则。
我的方案
(1)奖项设计。
奖项 奖项数量/个 奖品单价/元 奖品总价/元
一等奖
二等奖
三等奖
(2)抽奖设计。
道具介绍:转盘□扑克牌□彩球□(用打“√”的方式选择)
抽奖规则:(若选择“转盘”道具,可使用如图2表示规则)
【考点】游戏规则的公平性.
【专题】综合题;应用意识.
【答案】
奖项 奖项数量/个 奖品单价/元 奖品总价/元
一等奖 1 300 850
二等奖 2 100
三等奖 7 50
抽奖规则:盒子里面有3种颜色的10个彩球,其中红球1个,蓝球2个,绿球7个,摸到红球中一等奖,摸到蓝球中二等奖,摸到绿球中三等奖。
【分析】(1)根据利润=售卖价﹣进货价计算出10辆单车的盈利总额;然后设计合理的抽奖方案,既能让销售人员留有部分盈利金额还能带动消费;
(2)选择摸彩球的方式:盒子里面有3种颜色的10个彩球,其中红球1个,蓝球2个,绿球7个,摸到红球中一等奖,摸到蓝球中二等奖,摸到绿球中三等奖。据此设计即可。
【解答】解:(1)10×(780﹣650)=1300(元)
可以设计一等奖1个,奖品单价300元,二等奖2个,奖品单价100元,三等奖7个,奖品单价50元,则奖品总价为:
1×300+2×100+7×50
=300+200+350
=850(元)
850<1300,既能让销售人员留有部分盈利金额还能带动消费。
奖项设计如下:
奖项 奖项数量/个 奖品单价/元 奖品总价/元
一等奖 1 300 850
二等奖 2 100
三等奖 7 50
(2)选择摸彩球的方式:
抽奖规则:盒子里面有3种颜色的10个彩球,其中红球1个,蓝球2个,绿球7个,摸到红球中一等奖,摸到蓝球中二等奖,摸到绿球中三等奖。
故答案为:1;300;850;2;100;7;50。
【点评】本题考查了可能性大小及游戏规则的公平性的应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
