1.5.2 有理数的除法 课件(共31张PPT)
文档属性
| 名称 | 1.5.2 有理数的除法 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 06:03:39 | ||
图片预览









文档简介
(共31张PPT)
1.5.2 有理数的除法
第1章 有理数
【2024新教材】湘教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
1.5.2 有理数的除法教案
一、教学目标
(一)知识与技能目标
学生能准确理解有理数除法的意义,熟练掌握有理数除法法则,包括将除法转化为乘法的方法,即除以一个不等于\(0\)的数,等于乘这个数的倒数。
能够正确、熟练地运用有理数除法法则进行有理数的除法运算,以及有理数的乘除混合运算,准确处理运算中的符号和数值计算,提高运算能力。
(二)过程与方法目标
通过类比有理数乘法的学习过程,引导学生经历有理数除法法则的探究过程,培养学生的类比推理能力和知识迁移能力,提升数学思维的灵活性。
在解决有理数除法相关问题的过程中,培养学生分析问题、解决问题的能力,强化学生对数学转化思想的理解与应用。
(三)情感态度与价值观目标
让学生感受数学知识之间的内在联系和系统性,体会数学的逻辑性和严谨性,激发学生学习数学的兴趣和热情。
通过自主探索与合作交流,培养学生的团队合作精神和勇于挑战、敢于创新的精神,增强学生学习数学的自信心和成就感。
二、教学重难点
(一)教学重点
深入理解有理数除法法则,熟练掌握有理数除法运算转化为乘法运算的方法。
能够准确运用有理数除法法则进行有理数的除法及乘除混合运算,正确处理运算中的符号问题。
(二)教学难点
理解有理数除法法则的合理性,特别是负数参与除法运算时结果符号的确定。
在有理数乘除混合运算中,正确把握运算顺序,灵活运用运算律进行简便运算。
三、教学方法
讲授法、类比法、探究法、练习法相结合
四、教学过程
(一)复习回顾,情境导入(5 分钟)
知识回顾:同学们,之前我们学习了有理数的乘法及乘法运算律。谁能说一说有理数乘法法则?(两数相乘,同号得正,异号得负,并把绝对值相乘;任何数与\(0\)相乘,都得\(0\))乘法交换律、结合律、分配律的表达式分别是什么?(交换律\(a b = b a\),结合律\((a b) c = a (b c)\),分配律\(a (b + c)=a b + a c\))快速计算\(( - 3) 4\),\(( - 2) ( - 5)\) 。(学生计算后,教师点评并核对答案)
情境导入:老师这里有一个问题,小明有\(-12\)元钱,他想平均分给\(3\)个同学,每个同学能得到多少钱呢?这个问题就需要用到有理数的除法运算,今天我们就一起来学习有理数的除法。(板书课题:1.5.2 有理数的除法)
(二)新课讲授(20 分钟)
有理数除法的意义
回顾整数除法意义:在小学我们学过整数除法,它是乘法的逆运算,比如\(6 ·3 = 2\),是因为\(2 3 = 6\)。在有理数范围内,除法同样是乘法的逆运算。
结合实例理解:以刚才小明分钱的例子来说,\(( - 12) ·3\),我们要找一个数乘以\(3\)等于\(-12\),因为\(( - 4) 3 = - 12\),所以\(( - 12) ·3 = - 4\) 。这表明有理数除法是已知两个因数的积与其中一个因数,求另一个因数的运算。
有理数除法法则的推导
探究正数与负数相除:计算\(8 ·( - 4)\),思考哪个数乘以\(-4\)等于\(8\),因为\(( - 2) ( - 4)=8\),所以\(8 ·( - 4)= - 2\) 。
探究负数与正数相除:计算\(( - 8) ·4\),由于\(( - 2) 4 = - 8\),所以\(( - 8) ·4 = - 2\) 。
探究负数与负数相除:计算\(( - 8) ·( - 4)\),因为\(2 ( - 4)= - 8\),所以\(( - 8) ·( - 4)=2\) 。
探究\(0\)参与的除法:\(0 ·5 = 0\),因为\(0 5 = 0\);而\(5 ·0\)没有意义,因为找不到一个数乘以\(0\)等于\(5\),同样\(0 ·0\)也没有意义。
归纳法则:引导学生观察以上各种情况,小组讨论并归纳有理数除法法则:两数相除,同号得正,异号得负,并把绝对值相除。\(0\)除以任何一个不等于\(0\)的数,都得\(0\) 。同时,我们还可以将除法转化为乘法,除以一个不等于\(0\)的数,等于乘这个数的倒数,用式子表示为\(a ·b = a \frac{1}{b}(b 0)\) 。
有理数除法法则的应用
讲解例题:计算(1)\(( - 15) ·( - 3)\);(2)\(( - 12) ·\frac{1}{3}\);(3)\(0 ·( - 7)\) 。
解:(1)根据有理数除法法则,两数相除,同号得正,并把绝对值相除,\(( - 15) ·( - 3)=+(15 ·3)=5\);
(2)将除法转化为乘法,\(( - 12) ·\frac{1}{3}=( - 12) 3 = - 36\);
(3)\(0\)除以任何一个不等于\(0\)的数,都得\(0\),所以\(0 ·( - 7)=0\) 。
强调要点:在计算过程中,要先确定商的符号,再进行绝对值的运算;运用除法转化为乘法的方法时,要准确找到除数的倒数,同时注意符号问题。
(三)例题讲解(10 分钟)
例 1:计算\(( - \frac{3}{4}) ·( - \frac{9}{8})\)
解:将除法转化为乘法,\(( - \frac{3}{4}) ·( - \frac{9}{8})=( - \frac{3}{4}) ( - \frac{8}{9})\),根据有理数乘法法则,同号得正,并把绝对值相乘,\(( - \frac{3}{4}) ( - \frac{8}{9})=\frac{3 8}{4 9}=\frac{2}{3}\) 。
例 2:计算\(( - 24) ·( - 2) ·( - \frac{3}{4})\)
解:按照从左到右的顺序进行计算,先算\(( - 24) ·( - 2)=12\),再算\(12 ·( - \frac{3}{4})=12 ( - \frac{4}{3}) = - 16\) 。
通过这两个例题,详细展示有理数除法及乘除混合运算的步骤和方法,强调运算顺序和符号处理,规范解题格式,培养学生运用知识解决问题的能力。
(四)课堂练习(10 分钟)
计算下列各题
(1)\(24 ·( - 6)\);(2)\(( - 0.75) ·0.25\);(3)\(( - \frac{5}{6}) ·( - \frac{10}{3})\);(4)\(0 ·( - 100)\) 。
计算\(( - 18) ·( - 3) ( - \frac{1}{3})\),\(( - \frac{1}{2}) ·( - \frac{2}{3}) ·\frac{3}{4}\) 。
教师巡视学生练习情况,及时发现学生存在的问题,如符号错误、法则运用不熟练、运算顺序错误等,进行个别指导和集中讲解,帮助学生掌握有理数除法运算。
(五)课堂小结(5 分钟)
与学生一起回顾本节课所学内容
有理数除法的意义:除法是乘法的逆运算。
有理数除法法则:两数相除,同号得正,异号得负,并把绝对值相除;\(0\)除以任何一个不等于\(0\)的数,都得\(0\);除以一个不等于\(0\)的数,等于乘这个数的倒数。
有理数除法运算步骤:先确定商的符号,再进行绝对值运算,可将除法转化为乘法进行计算。
强调重点知识和易错点,如符号判断、倒数的计算、乘除混合运算的顺序等,帮助学生加深理解和记忆。
(六)作业布置(5 分钟)
书面作业:课本相关习题 [具体页码和题号],要求学生认真书写,规范解题步骤,准确运用有理数除法法则进行计算。
实践作业:观察生活中涉及有理数除法的实际问题,如平均分物品的价值计算等,记录下来并尝试用所学知识解决,下节课进行分享。
五、教学反思
在教学过程中,关注学生对有理数除法法则的理解和运用情况,分析学生在计算中出现错误的原因,如符号混淆、倒数计算错误、运算顺序混乱等。思考在后续教学中如何通过更多实例、针对性练习和有效辅导,帮助学生更好地掌握有理数除法运算,提高学生的运算能力和数学应用能力。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
情境导入
你能很快说出下列算式的结果吗?
乘法 除法
2×3=6 6÷2=
6÷3=
0×3=0 0÷3=
3
2
0
在小学,我们就知道除法是乘法的逆运算,
即 a÷b=a× (b≠0 )
那它在有理数的运算中也满足吗?
探索新知
我们知道 2 × 3 = 6, 因此
6 ÷ 3 = 2. ①
那么如何计算(-6)÷ 3,6 ÷(-3),(-6)÷(-3)呢?
探 究
在有理数中,除法也是乘法的逆运算.
有理数的除法法则1
由于 (-2)×3 = -6 ,
因此, (-6)÷3 = -2 . ②
类似地,由于(-2)×(-3)= 6 ,
由于 2 ×(-3) = -6 ,
因此, 6÷(- 3)= -2 , ③
因此, (-6)÷(-3)= 2 . ④
对于两个有理数a,b,其中 b不为0,如果有一个有理数c,使得 c b = a,那么规定 a ÷ b = c,且把 c 叫作 a 除以 b 的商.
抽 象
(-6)÷(-3)= 2 . ④
6 ÷ 3 = 2. ①
同号两数相除得正数,并把它们绝对值相除
(-6)÷3 = -2 . ②
6÷(- 3)= -2 , ③
异号两数相除得负数,并把它们绝对值相除
0÷(- 3)= 0.
0除以任何不等于0的数都得0
同号两数相除得正数,异号两数相除得负数,并把它们的绝对值相除;
0除以任何一个不等于0的数都得0.
(+)÷(+)→(+)
(-)÷(-)→(+)
(-)÷(+)→(-)
(+)÷(-)→(-)
计算:
(1)(-24)÷4 ; (2)(-18)÷(-9);
(3) 10 ÷(-5); (4) 0 ÷(-10).
(1)(-24)÷4 = -(24÷4) = -6 .
(2)(-18)÷(-9)= 18÷9= 2 .
(3) 10 ÷(-5)= -(10÷5)= -2 .
解
(4) 0÷(-10)= 0 .
先定符号;
再计算绝对值.
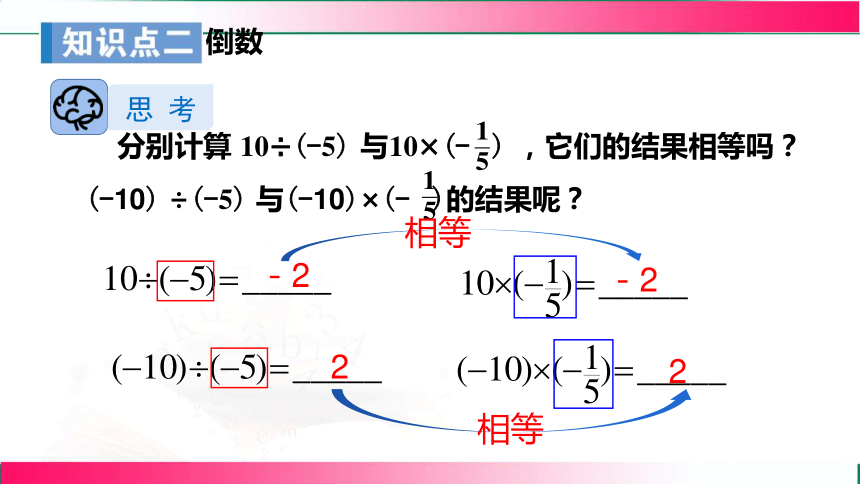
思 考
分别计算 10÷(-5) 与10×(- ) ,它们的结果相等吗?
(-10) ÷(-5) 与(-10)×(- )的结果呢?
-2
-2
2
2
相等
相等
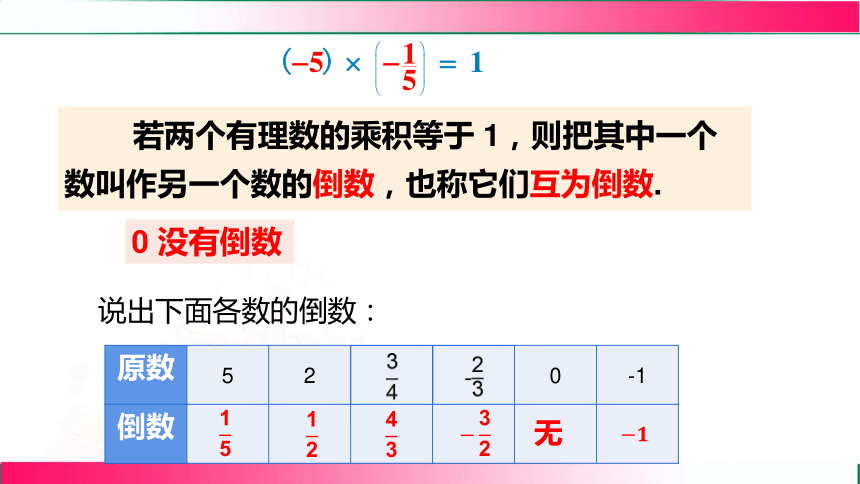
倒数
若两个有理数的乘积等于 1,则把其中一个数叫作另一个数的倒数,也称它们互为倒数.
0 没有倒数
原数 5 2 0 -1
倒数
说出下面各数的倒数:
无
有理数的除法法则2
⑤式表明,10 除以-5 等于10 乘-5 的倒数;
⑤
⑥
⑥式表明,-10 除以-5 等于-10 乘-5 的倒数.
填空:
1的倒数为________; -1的倒数为________;
的倒数为________; 的倒数为________;
0.25的倒数为________; 0的倒数________;
的倒数为________.
1
-1
3
4
不存在
注意:
1.求小数的倒数,先化成分数,再求倒数;
2.求带分数的倒数,先化成假分数,再求倒数;
3. 0没有倒数. 倒数是本身的数有±1.
一般地,有
除以一个不等于0的数等于乘这个数的倒数.
也可以表示为
除法变乘法
互为倒数
计算:
(1) ; (2) ;
(3) .
解
课堂练习
【课本P38 练习 第1题】
1. 计算:
(1)14÷(-7); (2)(-36)÷(-3);
(3)0÷(-0.618); (4)(-48)÷12.
(4) (-48)÷ 12 = -(48÷12)= -4 .
(3) 0÷(-0.618)= 0 .
(1) 14÷(-7)= -(14÷7) = -2 .
(2)(-36)÷(-3)= 36÷3= 12 .
解
2.填空:
(1)因为 × = 1,所以 的倒数是 ;
(2) 的倒数是 ;-3 的倒数是 .
-6
-6
【课本P38 练习 第2题】
3. 计算:
(1) (-36)÷(-0.6) ; (2) ;
(3) ; (4) .
【课本P38 练习 第3题】
(1) (-36)÷(-0.6)=36÷0.6= 60
解:
4. 已知 a,b,c 是有理数,当 a+b+c=0 ,abc<0 时,
的值为( )
A. 1 或 -3
B. 1 或 -1 或 -3
C. -1 或 3
D. 1 或 -1 或 3 或 -3
A
5.已知 a 与 b互为相反数,c与 d 互为倒数,m 的绝对值为6,求 的值.
解:由题意,得
因为a + b=0 ,cd =1 ,|m|=6
方法总结:解答此题的关键是先根据题意得出
a+b=0,cd=1及|m|=6,再代入所求代数式进行计算.
1. 下列各组数中,互为倒数的是( )
C
A. 0.5和5 B. 和
C. 5和 D. 和10
2. [2025永州期末] 的倒数的相反数是( )
D
A. B. C. D.
返回
3. 下列计算不正确的是( )
D
A. B.
C. D.
4. 下列化简:;; ;
; .其中正确的有( )
C
A. 1个 B. 2个 C. 3个 D. 4个
返回
5. 如图,要使的运算结果最小,则“ ”内应填入的运算
符号为( )
B
A. B. - C. × D.
【点拨】由数轴可知, ,
所以, ,
, .
因为 ,
所以“ ”内应填入的运算符号为“-”.
返回
6.点,表示的两个数在数轴上互为相反数,且点 向左平移
8个单位长度到达点,,表示的数互为倒数,则,, 三个
点所表示的数分别是___,____和____.
4
7.已知,,且,则 ____.
【点拨】因为,,且 ,
所以,或,,所以 .
返回
8.计算:
(1) ;
【解】
.
(2) .
.
返回
9.小溪在计算时,除号变乘号时,忘记把 改成它
的倒数,结果是54,则 的正确结果是__.
【点拨】由题意得,所以 ,所以
.
返回
10.小安和小何玩猜数的游戏,小安心里想好了一个数并描述
说:“这个数的绝对值等于它的相反数.”小何说:“我猜不到.”
小安继续说:“它的倒数等于它本身.”小何说“我知道了!”,
小安心里想的这个数是____.
11.规定,例如: ,则
的值为_ ___.
【点拨】由题意,得 ,
,故原式 .
返回
12.观察数列:1,2,4,8, 发现,从第二项起,每一项
与它前面的一项的比都是2.一般地,如果一列数从第二项起,
每一项与它前面的一项的比都等于同一个常数,我们就把这
样的一列数叫作等比数列.
(1)等比数列3,,27, 的第四项为_____;
(2)一个等比数列的第二项是5,第三项是 ,它的第一
项是____,第五项是_____.
返回
课堂小结
有理数的除法
法则一
法则二
同号两数相除得正数,异号两数相除得负数,并把它们的绝对值相除.
除以一个数等于乘这个数的倒数.
0除以任何一个不等于0的数都得0.
谢谢观看!
1.5.2 有理数的除法
第1章 有理数
【2024新教材】湘教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
1.5.2 有理数的除法教案
一、教学目标
(一)知识与技能目标
学生能准确理解有理数除法的意义,熟练掌握有理数除法法则,包括将除法转化为乘法的方法,即除以一个不等于\(0\)的数,等于乘这个数的倒数。
能够正确、熟练地运用有理数除法法则进行有理数的除法运算,以及有理数的乘除混合运算,准确处理运算中的符号和数值计算,提高运算能力。
(二)过程与方法目标
通过类比有理数乘法的学习过程,引导学生经历有理数除法法则的探究过程,培养学生的类比推理能力和知识迁移能力,提升数学思维的灵活性。
在解决有理数除法相关问题的过程中,培养学生分析问题、解决问题的能力,强化学生对数学转化思想的理解与应用。
(三)情感态度与价值观目标
让学生感受数学知识之间的内在联系和系统性,体会数学的逻辑性和严谨性,激发学生学习数学的兴趣和热情。
通过自主探索与合作交流,培养学生的团队合作精神和勇于挑战、敢于创新的精神,增强学生学习数学的自信心和成就感。
二、教学重难点
(一)教学重点
深入理解有理数除法法则,熟练掌握有理数除法运算转化为乘法运算的方法。
能够准确运用有理数除法法则进行有理数的除法及乘除混合运算,正确处理运算中的符号问题。
(二)教学难点
理解有理数除法法则的合理性,特别是负数参与除法运算时结果符号的确定。
在有理数乘除混合运算中,正确把握运算顺序,灵活运用运算律进行简便运算。
三、教学方法
讲授法、类比法、探究法、练习法相结合
四、教学过程
(一)复习回顾,情境导入(5 分钟)
知识回顾:同学们,之前我们学习了有理数的乘法及乘法运算律。谁能说一说有理数乘法法则?(两数相乘,同号得正,异号得负,并把绝对值相乘;任何数与\(0\)相乘,都得\(0\))乘法交换律、结合律、分配律的表达式分别是什么?(交换律\(a b = b a\),结合律\((a b) c = a (b c)\),分配律\(a (b + c)=a b + a c\))快速计算\(( - 3) 4\),\(( - 2) ( - 5)\) 。(学生计算后,教师点评并核对答案)
情境导入:老师这里有一个问题,小明有\(-12\)元钱,他想平均分给\(3\)个同学,每个同学能得到多少钱呢?这个问题就需要用到有理数的除法运算,今天我们就一起来学习有理数的除法。(板书课题:1.5.2 有理数的除法)
(二)新课讲授(20 分钟)
有理数除法的意义
回顾整数除法意义:在小学我们学过整数除法,它是乘法的逆运算,比如\(6 ·3 = 2\),是因为\(2 3 = 6\)。在有理数范围内,除法同样是乘法的逆运算。
结合实例理解:以刚才小明分钱的例子来说,\(( - 12) ·3\),我们要找一个数乘以\(3\)等于\(-12\),因为\(( - 4) 3 = - 12\),所以\(( - 12) ·3 = - 4\) 。这表明有理数除法是已知两个因数的积与其中一个因数,求另一个因数的运算。
有理数除法法则的推导
探究正数与负数相除:计算\(8 ·( - 4)\),思考哪个数乘以\(-4\)等于\(8\),因为\(( - 2) ( - 4)=8\),所以\(8 ·( - 4)= - 2\) 。
探究负数与正数相除:计算\(( - 8) ·4\),由于\(( - 2) 4 = - 8\),所以\(( - 8) ·4 = - 2\) 。
探究负数与负数相除:计算\(( - 8) ·( - 4)\),因为\(2 ( - 4)= - 8\),所以\(( - 8) ·( - 4)=2\) 。
探究\(0\)参与的除法:\(0 ·5 = 0\),因为\(0 5 = 0\);而\(5 ·0\)没有意义,因为找不到一个数乘以\(0\)等于\(5\),同样\(0 ·0\)也没有意义。
归纳法则:引导学生观察以上各种情况,小组讨论并归纳有理数除法法则:两数相除,同号得正,异号得负,并把绝对值相除。\(0\)除以任何一个不等于\(0\)的数,都得\(0\) 。同时,我们还可以将除法转化为乘法,除以一个不等于\(0\)的数,等于乘这个数的倒数,用式子表示为\(a ·b = a \frac{1}{b}(b 0)\) 。
有理数除法法则的应用
讲解例题:计算(1)\(( - 15) ·( - 3)\);(2)\(( - 12) ·\frac{1}{3}\);(3)\(0 ·( - 7)\) 。
解:(1)根据有理数除法法则,两数相除,同号得正,并把绝对值相除,\(( - 15) ·( - 3)=+(15 ·3)=5\);
(2)将除法转化为乘法,\(( - 12) ·\frac{1}{3}=( - 12) 3 = - 36\);
(3)\(0\)除以任何一个不等于\(0\)的数,都得\(0\),所以\(0 ·( - 7)=0\) 。
强调要点:在计算过程中,要先确定商的符号,再进行绝对值的运算;运用除法转化为乘法的方法时,要准确找到除数的倒数,同时注意符号问题。
(三)例题讲解(10 分钟)
例 1:计算\(( - \frac{3}{4}) ·( - \frac{9}{8})\)
解:将除法转化为乘法,\(( - \frac{3}{4}) ·( - \frac{9}{8})=( - \frac{3}{4}) ( - \frac{8}{9})\),根据有理数乘法法则,同号得正,并把绝对值相乘,\(( - \frac{3}{4}) ( - \frac{8}{9})=\frac{3 8}{4 9}=\frac{2}{3}\) 。
例 2:计算\(( - 24) ·( - 2) ·( - \frac{3}{4})\)
解:按照从左到右的顺序进行计算,先算\(( - 24) ·( - 2)=12\),再算\(12 ·( - \frac{3}{4})=12 ( - \frac{4}{3}) = - 16\) 。
通过这两个例题,详细展示有理数除法及乘除混合运算的步骤和方法,强调运算顺序和符号处理,规范解题格式,培养学生运用知识解决问题的能力。
(四)课堂练习(10 分钟)
计算下列各题
(1)\(24 ·( - 6)\);(2)\(( - 0.75) ·0.25\);(3)\(( - \frac{5}{6}) ·( - \frac{10}{3})\);(4)\(0 ·( - 100)\) 。
计算\(( - 18) ·( - 3) ( - \frac{1}{3})\),\(( - \frac{1}{2}) ·( - \frac{2}{3}) ·\frac{3}{4}\) 。
教师巡视学生练习情况,及时发现学生存在的问题,如符号错误、法则运用不熟练、运算顺序错误等,进行个别指导和集中讲解,帮助学生掌握有理数除法运算。
(五)课堂小结(5 分钟)
与学生一起回顾本节课所学内容
有理数除法的意义:除法是乘法的逆运算。
有理数除法法则:两数相除,同号得正,异号得负,并把绝对值相除;\(0\)除以任何一个不等于\(0\)的数,都得\(0\);除以一个不等于\(0\)的数,等于乘这个数的倒数。
有理数除法运算步骤:先确定商的符号,再进行绝对值运算,可将除法转化为乘法进行计算。
强调重点知识和易错点,如符号判断、倒数的计算、乘除混合运算的顺序等,帮助学生加深理解和记忆。
(六)作业布置(5 分钟)
书面作业:课本相关习题 [具体页码和题号],要求学生认真书写,规范解题步骤,准确运用有理数除法法则进行计算。
实践作业:观察生活中涉及有理数除法的实际问题,如平均分物品的价值计算等,记录下来并尝试用所学知识解决,下节课进行分享。
五、教学反思
在教学过程中,关注学生对有理数除法法则的理解和运用情况,分析学生在计算中出现错误的原因,如符号混淆、倒数计算错误、运算顺序混乱等。思考在后续教学中如何通过更多实例、针对性练习和有效辅导,帮助学生更好地掌握有理数除法运算,提高学生的运算能力和数学应用能力。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
情境导入
你能很快说出下列算式的结果吗?
乘法 除法
2×3=6 6÷2=
6÷3=
0×3=0 0÷3=
3
2
0
在小学,我们就知道除法是乘法的逆运算,
即 a÷b=a× (b≠0 )
那它在有理数的运算中也满足吗?
探索新知
我们知道 2 × 3 = 6, 因此
6 ÷ 3 = 2. ①
那么如何计算(-6)÷ 3,6 ÷(-3),(-6)÷(-3)呢?
探 究
在有理数中,除法也是乘法的逆运算.
有理数的除法法则1
由于 (-2)×3 = -6 ,
因此, (-6)÷3 = -2 . ②
类似地,由于(-2)×(-3)= 6 ,
由于 2 ×(-3) = -6 ,
因此, 6÷(- 3)= -2 , ③
因此, (-6)÷(-3)= 2 . ④
对于两个有理数a,b,其中 b不为0,如果有一个有理数c,使得 c b = a,那么规定 a ÷ b = c,且把 c 叫作 a 除以 b 的商.
抽 象
(-6)÷(-3)= 2 . ④
6 ÷ 3 = 2. ①
同号两数相除得正数,并把它们绝对值相除
(-6)÷3 = -2 . ②
6÷(- 3)= -2 , ③
异号两数相除得负数,并把它们绝对值相除
0÷(- 3)= 0.
0除以任何不等于0的数都得0
同号两数相除得正数,异号两数相除得负数,并把它们的绝对值相除;
0除以任何一个不等于0的数都得0.
(+)÷(+)→(+)
(-)÷(-)→(+)
(-)÷(+)→(-)
(+)÷(-)→(-)
计算:
(1)(-24)÷4 ; (2)(-18)÷(-9);
(3) 10 ÷(-5); (4) 0 ÷(-10).
(1)(-24)÷4 = -(24÷4) = -6 .
(2)(-18)÷(-9)= 18÷9= 2 .
(3) 10 ÷(-5)= -(10÷5)= -2 .
解
(4) 0÷(-10)= 0 .
先定符号;
再计算绝对值.
思 考
分别计算 10÷(-5) 与10×(- ) ,它们的结果相等吗?
(-10) ÷(-5) 与(-10)×(- )的结果呢?
-2
-2
2
2
相等
相等
倒数
若两个有理数的乘积等于 1,则把其中一个数叫作另一个数的倒数,也称它们互为倒数.
0 没有倒数
原数 5 2 0 -1
倒数
说出下面各数的倒数:
无
有理数的除法法则2
⑤式表明,10 除以-5 等于10 乘-5 的倒数;
⑤
⑥
⑥式表明,-10 除以-5 等于-10 乘-5 的倒数.
填空:
1的倒数为________; -1的倒数为________;
的倒数为________; 的倒数为________;
0.25的倒数为________; 0的倒数________;
的倒数为________.
1
-1
3
4
不存在
注意:
1.求小数的倒数,先化成分数,再求倒数;
2.求带分数的倒数,先化成假分数,再求倒数;
3. 0没有倒数. 倒数是本身的数有±1.
一般地,有
除以一个不等于0的数等于乘这个数的倒数.
也可以表示为
除法变乘法
互为倒数
计算:
(1) ; (2) ;
(3) .
解
课堂练习
【课本P38 练习 第1题】
1. 计算:
(1)14÷(-7); (2)(-36)÷(-3);
(3)0÷(-0.618); (4)(-48)÷12.
(4) (-48)÷ 12 = -(48÷12)= -4 .
(3) 0÷(-0.618)= 0 .
(1) 14÷(-7)= -(14÷7) = -2 .
(2)(-36)÷(-3)= 36÷3= 12 .
解
2.填空:
(1)因为 × = 1,所以 的倒数是 ;
(2) 的倒数是 ;-3 的倒数是 .
-6
-6
【课本P38 练习 第2题】
3. 计算:
(1) (-36)÷(-0.6) ; (2) ;
(3) ; (4) .
【课本P38 练习 第3题】
(1) (-36)÷(-0.6)=36÷0.6= 60
解:
4. 已知 a,b,c 是有理数,当 a+b+c=0 ,abc<0 时,
的值为( )
A. 1 或 -3
B. 1 或 -1 或 -3
C. -1 或 3
D. 1 或 -1 或 3 或 -3
A
5.已知 a 与 b互为相反数,c与 d 互为倒数,m 的绝对值为6,求 的值.
解:由题意,得
因为a + b=0 ,cd =1 ,|m|=6
方法总结:解答此题的关键是先根据题意得出
a+b=0,cd=1及|m|=6,再代入所求代数式进行计算.
1. 下列各组数中,互为倒数的是( )
C
A. 0.5和5 B. 和
C. 5和 D. 和10
2. [2025永州期末] 的倒数的相反数是( )
D
A. B. C. D.
返回
3. 下列计算不正确的是( )
D
A. B.
C. D.
4. 下列化简:;; ;
; .其中正确的有( )
C
A. 1个 B. 2个 C. 3个 D. 4个
返回
5. 如图,要使的运算结果最小,则“ ”内应填入的运算
符号为( )
B
A. B. - C. × D.
【点拨】由数轴可知, ,
所以, ,
, .
因为 ,
所以“ ”内应填入的运算符号为“-”.
返回
6.点,表示的两个数在数轴上互为相反数,且点 向左平移
8个单位长度到达点,,表示的数互为倒数,则,, 三个
点所表示的数分别是___,____和____.
4
7.已知,,且,则 ____.
【点拨】因为,,且 ,
所以,或,,所以 .
返回
8.计算:
(1) ;
【解】
.
(2) .
.
返回
9.小溪在计算时,除号变乘号时,忘记把 改成它
的倒数,结果是54,则 的正确结果是__.
【点拨】由题意得,所以 ,所以
.
返回
10.小安和小何玩猜数的游戏,小安心里想好了一个数并描述
说:“这个数的绝对值等于它的相反数.”小何说:“我猜不到.”
小安继续说:“它的倒数等于它本身.”小何说“我知道了!”,
小安心里想的这个数是____.
11.规定,例如: ,则
的值为_ ___.
【点拨】由题意,得 ,
,故原式 .
返回
12.观察数列:1,2,4,8, 发现,从第二项起,每一项
与它前面的一项的比都是2.一般地,如果一列数从第二项起,
每一项与它前面的一项的比都等于同一个常数,我们就把这
样的一列数叫作等比数列.
(1)等比数列3,,27, 的第四项为_____;
(2)一个等比数列的第二项是5,第三项是 ,它的第一
项是____,第五项是_____.
返回
课堂小结
有理数的除法
法则一
法则二
同号两数相除得正数,异号两数相除得负数,并把它们的绝对值相除.
除以一个数等于乘这个数的倒数.
0除以任何一个不等于0的数都得0.
谢谢观看!
同课章节目录
