2.4.2整式的加法与减法 课件(共38张PPT)
文档属性
| 名称 | 2.4.2整式的加法与减法 课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 06:41:12 | ||
图片预览











文档简介
(共38张PPT)
2.4.2整式的加法与减法
第2章 代数式
【2024新教材】湘教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
2.4.2 整式的加法与减法
一、知识回顾
在学习整式的加法与减法之前,我们需要先回顾两个重要的知识点:同类项和去括号法则。
(一)同类项
同类项是指所含字母相同,并且相同字母的指数也相同的项 。例如,\(3x^2y\)与\( - 5x^2y\),它们都含有字母\(x\)和\(y\),且\(x\)的指数都是\(2\),\(y\)的指数都是\(1\),所以是同类项;所有的常数项也是同类项,像\(5\)和\( - 3\) 。同类项的概念是整式加减法的重要基础,在运算过程中,我们常常需要找出同类项进行合并。
(二)去括号法则
当括号前是 “\(+\)” 号时,把括号和它前面的 “\(+\)” 号去掉后,原括号里各项的符号都不改变 。例如,\(a + (b + c)=a + b + c\) 。
当括号前是 “\(-\)” 号时,把括号和它前面的 “\(-\)” 号去掉后,原括号里各项的符号都要改变 。例如,\(a - (b - c)=a - b + c\) 。
当括号前是数字因数时,应利用乘法分配律先将数字因数与括号内的各项分别相乘,再去括号 。例如,\(3(2x - 1)=3 2x - 3 1 = 6x - 3\) 。去括号法则在整式加减法中用于化简式子,使运算能够顺利进行。
二、整式的加法与减法的概念
整式的加法与减法运算,实际上就是对整式中的同类项进行合并,在有括号的情况下,先去括号,再合并同类项 。整式的加减法可以帮助我们简化复杂的整式表达式,更清晰地呈现式子的结构和数量关系,在解决实际问题和进一步学习代数知识中都有着广泛的应用。
三、整式的加法与减法的运算步骤
(一)去括号
如果整式中含有括号,根据括号前的符号,运用去括号法则去掉括号 。例如对于式子\((2x^2 - 3x + 1) - (x^2 + 2x - 5)\),根据去括号法则,去掉括号后变为\(2x^2 - 3x + 1 - x^2 - 2x + 5\) 。
(二)找出同类项
仔细观察去括号后的式子,根据同类项的定义,找出其中的同类项 。在\(2x^2 - 3x + 1 - x^2 - 2x + 5\)中,\(2x^2\)与\(-x^2\)是同类项,\(-3x\)与\(-2x\)是同类项,\(1\)与\(5\)是同类项 。
(三)合并同类项
把同类项的系数相加,字母和字母的指数不变,将同类项合并成一项 。对于上述式子,合并同类项可得:\((2x^2 - x^2)+(-3x - 2x)+(1 + 5)=x^2 - 5x + 6\) 。
四、典型例题讲解
(一)简单整式的加减法
例 1:计算\((3x + 2y)+(4x - 3y)\)
解析:
去括号:式子中括号前都是 “\(+\)” 号,根据去括号法则,去括号后各项符号不变,得到\(3x + 2y + 4x - 3y\) 。
找出同类项:\(3x\)与\(4x\)是同类项,\(2y\)与\(-3y\)是同类项 。
合并同类项:\((3x + 4x)+(2y - 3y)=7x - y\) 。
(二)复杂整式的加减法
例 2:计算\(3(2a^2 - b^2) - 2(3a^2 + 2b^2)\)
解析:
去括号:根据括号前是数字因数的去括号法则,利用乘法分配律去括号,\(3(2a^2 - b^2)=3 2a^2 - 3 b^2 = 6a^2 - 3b^2\),\(-2(3a^2 + 2b^2)= - 2 3a^2 - 2 2b^2 = - 6a^2 - 4b^2\),原式变为\(6a^2 - 3b^2 - 6a^2 - 4b^2\) 。
找出同类项:\(6a^2\)与\(-6a^2\)是同类项,\(-3b^2\)与\(-4b^2\)是同类项 。
合并同类项:\((6a^2 - 6a^2)+(-3b^2 - 4b^2)= - 7b^2\) 。
(三)整式加减法在实际问题中的应用
例 3:一个长方形的长为\((3x + 2y)\)厘米,宽比长少\((x - y)\)厘米,求这个长方形的周长。
解析:
先求出长方形的宽:宽为\((3x + 2y) - (x - y)\),去括号得\(3x + 2y - x + y\),合并同类项得\(2x + 3y\)厘米 。
再根据长方形周长公式计算周长:周长\(C = 2[(3x + 2y)+(2x + 3y)]\),去括号得\(2(3x + 2y + 2x + 3y)\),合并同类项得\(2(5x + 5y)\),再利用乘法分配律得\(10x + 10y\)厘米 。
所以,这个长方形的周长是\((10x + 10y)\)厘米 。
五、易错点分析
去括号时符号错误:当括号前是 “\(-\)” 号,容易忘记改变原括号里各项的符号;当括号前是数字因数时,可能出现乘法分配律使用错误,没有将数字因数与括号内的每一项都相乘 。例如在计算\(2 - (3x - 1)\)时,错误地得到\(2 - 3x - 1\),正确的应该是\(2 - 3x + 1\);计算\(2(3x + 2)\)时,错误写成\(6x + 2\),正确结果是\(6x + 4\) 。
合并同类项错误:找错同类项或者在合并同类项时,错误地对字母或字母的指数进行了运算 。比如把\(3x^2\)与\(3x\)当作同类项合并,或者在合并\(2x^2 + 3x^2\)时,错误地得到\(5x^4\) 。
运算顺序错误:在整式加减法中,有括号的要先去括号,再合并同类项。如果没有按照正确的顺序进行运算,就会得到错误的结果 。例如对于式子\((2x + 3) - (x - 1) + 2x\),如果先计算\(2x + 3 - x\),就会出现错误,应该先去括号得到\(2x + 3 - x + 1 + 2x\),再合并同类项 。
通过以上对整式的加法与减法的学习,我们了解了其运算的基础、概念、步骤、应用以及易错点。在实际运算过程中,要认真仔细,准确运用去括号法则和合并同类项的方法,提高运算的准确性。如果还有任何疑问,欢迎随时探讨。
这份内容围绕整式加减法展开,从基础到应用逐步深入。若你觉得某些部分讲解不够详细,或想增加特定类型例题,欢迎提出,我们一起优化。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
复习导入
合并同类项:系数相加,字母及其指数不变.
去括号:括号前是“+”号,去括号后括号里各项不变号.
去括号:括号前是“-”号,去括号后括号里各项都变号.
5x+2x-4x= _________= _________ .
x+(a-b) = _________.
x- (a-b) = _________.
(5+2-4)x
3x
x+a-b
x-a+b
去括号依据:乘法分配律:a (b+c) = ab+ac
选择题
1.下列去括号,正确的是 ( )
A. a-(b+c)=a-b-c B. a+(b-c)=a+b+c
C. a-(b+c)=a-b+c D. a-(b+c)=a+b-c
2.在 -( )=-x2+3x-2 的括号里应填上的代数式是 ( )
A. x2-3x-2 B. x2+3x-2
C. x2-3x+2 D. x2+3x+2
3.下列各式中与多项式 2x-3y+4z 相等的是 ( )
A.2x+(3y-4z) B. 2x-(3y-4z)
C. 2x+(3y+4z) D. 2x-(3y+4z)
A
C
B
探索新知
思 考
计算:3(xy-2y)-5(x-2y+1)=____________.
规定:整式的加法满足乘法对加法的分配律.
3(xy-2y)-5(x-2y+1)
= (3xy-6y)-(5x-10y+5)
= 3xy__6y__5x__10y__5
= 3xy-5x+4y-5 .
3xy-5x+4y-5
乘法对加法的分配律
去括号
合并同类项
-
-
+
-
结果为整式
例3
计算:(3x2y3-xy2)-2(x2y3+6xy2)+(-4x2y3+ 2xy2).
(3x2y3-xy2)-2(x2y3+6xy2)+(-4x2y3+ 2xy2)
解
=3x2y3-xy2-(2x2y3+12xy2)-4x2y3+ 2xy2
=3x2y3-xy2-2x2y3-12xy2-4x2y3+2xy2
=[3+(-2) +(-4)]x2y3 +[(-1)+(-12) +2]xy2
=-3x2y3-11xy2 .
去括号和合并同类项是整式的加减运算的基础.
“整式的加减”的一般步骤为:
①有括号,根据去括号法则去括号;
②找同类项,按照合并同类项法则合并同类项.
整式的加减运算的结果仍为整式.
注意:整式的加减运算的结果要求最简,
也就是运算结果中不能再有同类项.
练一练
1.计算:
(1) 3(x+y)-5(x+y)+(x+y);
(2) 5(3x2-2y)-4(2x+3y2)+(3x2-2y)-3(2x+3y2).
(1) 3(x+y)-5(x+y)+(x+y)
= (3x+3y)-(5x+5y)+(x+y)
= 3x+3y -5x- 5y+x+y
= (3-5+1)x +(3-5+1)y
= -x -y
(1) 3(x+y)-5(x+y)+(x+y)
= (3-5+1)(x+y)
= -x -y
= -(x+y)
方法2:
练一练
1.计算:
(1) 3(x+y)-5(x+y)+(x+y);
(2) 5(3x2-2y)-4(2x+3y2)+(3x2-2y)-3(2x+3y2).
(2) 5(3x2-2y)-4(2x+3y2)+(3x2-2y)-3(2x+3y2)
= (15x2-10y)-(8x+12y2)+3x2-2y- (6x+9y2)
= 15x2-10y-8x-12y2+3x2-2y-6x-9y2
= (15+3)x2+[(-8)+(-6)]x+[(-12)+(-9)]y2+[(-10)+(-2)]y
= 18x2-14x-21y2-12y .
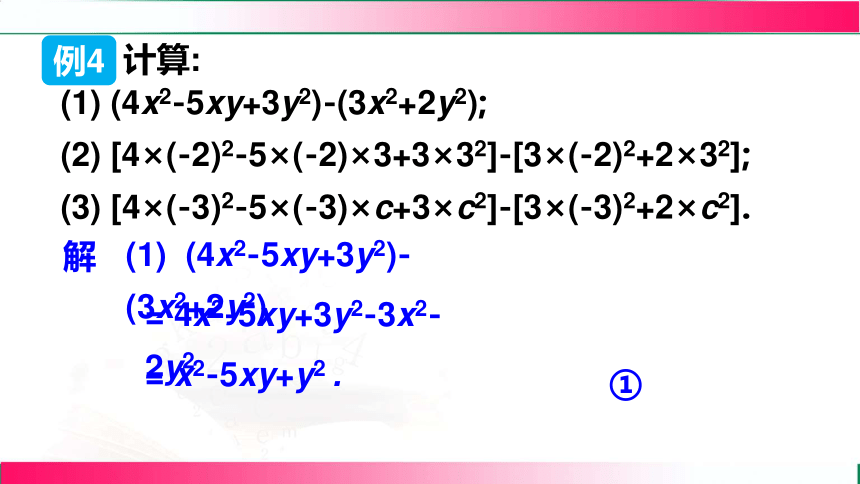
例4
计算:
(1) (4x2-5xy+3y2)-(3x2+2y2);
(2) [4×(-2)2-5×(-2)×3+3×32]-[3×(-2)2+2×32];
(3) [4×(-3)2-5×(-3)×c+3×c2]-[3×(-3)2+2×c2].
分析:将(2)与(1)进行比较,可以发现:将(1)中的字母 x,y 分别用-2,3代入即可得(2),于是只需将(1)的结果中的字母 x,y 分别用-2,3代入,即可得(2)的结果,这样能大大减少运算量.类似地,可以求得(3)的计算结果.
例4
计算:
解
(1) (4x2-5xy+3y2)-(3x2+2y2)
= 4x2-5xy+3y2-3x2-2y2
= x2-5xy+y2 .
①
(1) (4x2-5xy+3y2)-(3x2+2y2);
(2) [4×(-2)2-5×(-2)×3+3×32]-[3×(-2)2+2×32];
(3) [4×(-3)2-5×(-3)×c+3×c2]-[3×(-3)2+2×c2].
例4
计算:
(2) 将等式①中的x 用-2,y用3代入,则
= x2-5xy+y2 .
[4×(-2)2-5×(-2)×3+3×32]-[3×(-2)2+2×32]
= (-2)2-5×(-2)×3+32
= 4+30+9
= 43 .
(1) (4x2-5xy+3y2)-(3x2+2y2);
(2) [4×(-2)2-5×(-2)×3+3×32]-[3×(-2)2+2×32];
(3) [4×(-3)2-5×(-3)×c+3×c2]-[3×(-3)2+2×c2].
例4
计算:
(3) 将等式①中的 x 用-3,y用 c 代入,则
= x2-5xy+y2 .
[4×(-3)2-5×(-3)×c+3×c2]-[3×(-3)2+2×c2]
= (-3)2-5×(-3)×c+c2
= 9+15c+c2
(1) (4x2-5xy+3y2)-(3x2+2y2);
(2) [4×(-2)2-5×(-2)×3+3×32]-[3×(-2)2+2×32];
(3) [4×(-3)2-5×(-3)×c+3×c2]-[3×(-3)2+2×c2].
练一练
1.先计算 2(x3y2-5xy3+x)+(3xy3-2x)-3(x3y2-xy3+7x),
再利用所得结果计算:2×[(-1)3×(-2)2-5×(-1)×(-2)3+(-1)] +[3 ×(-1) ×(-2)3-2 ×(-1)]-3× [(-1) 3×(-2)2- (-1)×(-2)3+7 ×(-1)] .
2(x3y2-5xy3+x)+(3xy3-2x)-3(x3y2-xy3+7x)
=(2x3y2-10xy3+2x)+3xy3-2x- (3x3y2-3xy3+21x)
=2x3y2-10xy3+2x+3xy3-2x- 3x3y2+3xy3-21x
=-x3y2-4xy3-21x
将x=-1,y=-2代入上式结果得,
- (-1)3×(-2)2-4×(-1) ×(-2)3-21×(-1)=-7 .
解:
【课本P86 习题2.4第4题】
课堂练习
1.一个多项式加上 -2+x-x2 得到 x2-1 ,则这个多项式是_________.
2.多项式x2-3kxy-3y2+xy-8 化简后不含 xy 项 ,则k 为_________.
2x2-x+1
3.计算:
(1) (-3x2y2+5xy-y3)+3(7x2y2-xy+4y3);
(2) (x3+5x-1)-3(2x3-3x2)+(4x2-5x+6);
(3) 4(-2x3+4x)+(x3-5x2+1)-2(-x3+x);
(4) (x3y-3x2y2-x)+4(2x3y-x2y2)-3(-x3y+6x2y2) .
解:
(1) 18x2y2+2xy+11y3;
(2) -5x3+10x2+5;
(3) -5x3-5x2+14x+1;
(4) 12x3y-25x2y2-x .
【课本P85 练习题】
4.小王认为:代数式 x2+x(x+y)-2x2-xy 的值与x,y的取值无关,你认为呢?试说明理由.
解:无关.
x2+x(x+y)-2x2-xy
=x2+x2+xy-2x2-xy
=(1+1-2)x2+(1-1)xy
=0
1. 与 的和为( )
A
A. B.
C. D.
返回
2. 某同学在完成化简:
的过程中,具体步骤如下:
解:原式
.③
以上解题过程中,出现错误的步骤是( )
C
A. ① B. ② C. ③ D. ①②③
返回
3. [2025邵阳月考]下面是小芳做的一道多项式的加减运算
题,但她不小心把一滴墨水滴在了上面:
,阴影部分即为被墨水弄污的部分,那么阴影部
分应是( )
D
A. B. C. D.
返回
4.某客车上原有 人,中途有一半人下车,又上来若
干人,这时车上共有乘客 人,则上车乘客是_____
_________人.
返回
5. 已知,, 三个有理数在数轴上的位置
如图所示.化简: _______.
【点拨】因为,所以, ,
,所以 .
返回
6.化简:
(1) ;
【解】原式 .
(2) .
原式
.
返回
7.先化简,再求值:
,其中 ,
.
【解】原式
,
当, 时,
原式 .
返回
8. 一个三位数的百位数字为,十位数字为,个位数字为 ,
若把它的百位数字与个位数字对调得到一个新数.计算原数与
新数的差,则下列各数一定能整除这个差的是( )
A
A. 11 B. 7 C. 5 D. 2
【点拨】原数-新数 ,故选A.
返回
9. 某果园引入了 个采摘机器人,这些机器人被分为两组,
每组的工作效率不同.第一组有 个机器人,每个机器人平均8
秒采摘一个苹果;第二组包含剩余的机器人,每个机器人平
均6秒采摘一个苹果.同时,果园内还有10名熟练的采摘工人,
他们每个人平均5秒采摘一个苹果.机器人与工人同时工作1小
时,则这 个机器人比这10名工人多采摘的苹果个数是
( )
B
A. B.
C. D.
返回
10. 若,,则 可以表示
为( )
C
A. B. C. D.
【点拨】因为,所以 .
返回
11. 如图,在一个长方形中放入三个正
方形,边长分别为,, ,若要求出
右上角阴影部分周长与左下角阴影部分
周长的差,则只需知道,, 中哪个
量( )
C
A. B.
C. D. ,, 中任意一个
【点拨】设重叠部分的小长方形的长为 ,宽为
,则右上角阴影部
,所以右上角阴影部分周长为 ,左下角阴影部分周长为
分周长与左下角阴影部分周长的差可表示为.所以只需知道,,中的 即可.
返回
12. 在数学中,为了书写简便,18世纪数学家
欧拉就引进了求和符号“ ”.如
,
,
.若
,则常数, 的值分别
是_________.
,54
【点拨】因为
,所以易知 ,所以
,所以
,即 ,所以
, .
返回
13. 定义新运算: .例如:
.
(1)计算: ,并写出其结果的次数和
项数;
【解】原式
.
的次数为2,项数为3.
(2)若与 互为相反数,求(1)中结果
的值.
因为与 互为相反数,
所以 ,
所以, ,
所以, ,
所以(1)中原式
.
返回
课堂小结
整式的加减
步骤
应用
去括号
合并同类项
谢谢观看!
2.4.2整式的加法与减法
第2章 代数式
【2024新教材】湘教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
2.4.2 整式的加法与减法
一、知识回顾
在学习整式的加法与减法之前,我们需要先回顾两个重要的知识点:同类项和去括号法则。
(一)同类项
同类项是指所含字母相同,并且相同字母的指数也相同的项 。例如,\(3x^2y\)与\( - 5x^2y\),它们都含有字母\(x\)和\(y\),且\(x\)的指数都是\(2\),\(y\)的指数都是\(1\),所以是同类项;所有的常数项也是同类项,像\(5\)和\( - 3\) 。同类项的概念是整式加减法的重要基础,在运算过程中,我们常常需要找出同类项进行合并。
(二)去括号法则
当括号前是 “\(+\)” 号时,把括号和它前面的 “\(+\)” 号去掉后,原括号里各项的符号都不改变 。例如,\(a + (b + c)=a + b + c\) 。
当括号前是 “\(-\)” 号时,把括号和它前面的 “\(-\)” 号去掉后,原括号里各项的符号都要改变 。例如,\(a - (b - c)=a - b + c\) 。
当括号前是数字因数时,应利用乘法分配律先将数字因数与括号内的各项分别相乘,再去括号 。例如,\(3(2x - 1)=3 2x - 3 1 = 6x - 3\) 。去括号法则在整式加减法中用于化简式子,使运算能够顺利进行。
二、整式的加法与减法的概念
整式的加法与减法运算,实际上就是对整式中的同类项进行合并,在有括号的情况下,先去括号,再合并同类项 。整式的加减法可以帮助我们简化复杂的整式表达式,更清晰地呈现式子的结构和数量关系,在解决实际问题和进一步学习代数知识中都有着广泛的应用。
三、整式的加法与减法的运算步骤
(一)去括号
如果整式中含有括号,根据括号前的符号,运用去括号法则去掉括号 。例如对于式子\((2x^2 - 3x + 1) - (x^2 + 2x - 5)\),根据去括号法则,去掉括号后变为\(2x^2 - 3x + 1 - x^2 - 2x + 5\) 。
(二)找出同类项
仔细观察去括号后的式子,根据同类项的定义,找出其中的同类项 。在\(2x^2 - 3x + 1 - x^2 - 2x + 5\)中,\(2x^2\)与\(-x^2\)是同类项,\(-3x\)与\(-2x\)是同类项,\(1\)与\(5\)是同类项 。
(三)合并同类项
把同类项的系数相加,字母和字母的指数不变,将同类项合并成一项 。对于上述式子,合并同类项可得:\((2x^2 - x^2)+(-3x - 2x)+(1 + 5)=x^2 - 5x + 6\) 。
四、典型例题讲解
(一)简单整式的加减法
例 1:计算\((3x + 2y)+(4x - 3y)\)
解析:
去括号:式子中括号前都是 “\(+\)” 号,根据去括号法则,去括号后各项符号不变,得到\(3x + 2y + 4x - 3y\) 。
找出同类项:\(3x\)与\(4x\)是同类项,\(2y\)与\(-3y\)是同类项 。
合并同类项:\((3x + 4x)+(2y - 3y)=7x - y\) 。
(二)复杂整式的加减法
例 2:计算\(3(2a^2 - b^2) - 2(3a^2 + 2b^2)\)
解析:
去括号:根据括号前是数字因数的去括号法则,利用乘法分配律去括号,\(3(2a^2 - b^2)=3 2a^2 - 3 b^2 = 6a^2 - 3b^2\),\(-2(3a^2 + 2b^2)= - 2 3a^2 - 2 2b^2 = - 6a^2 - 4b^2\),原式变为\(6a^2 - 3b^2 - 6a^2 - 4b^2\) 。
找出同类项:\(6a^2\)与\(-6a^2\)是同类项,\(-3b^2\)与\(-4b^2\)是同类项 。
合并同类项:\((6a^2 - 6a^2)+(-3b^2 - 4b^2)= - 7b^2\) 。
(三)整式加减法在实际问题中的应用
例 3:一个长方形的长为\((3x + 2y)\)厘米,宽比长少\((x - y)\)厘米,求这个长方形的周长。
解析:
先求出长方形的宽:宽为\((3x + 2y) - (x - y)\),去括号得\(3x + 2y - x + y\),合并同类项得\(2x + 3y\)厘米 。
再根据长方形周长公式计算周长:周长\(C = 2[(3x + 2y)+(2x + 3y)]\),去括号得\(2(3x + 2y + 2x + 3y)\),合并同类项得\(2(5x + 5y)\),再利用乘法分配律得\(10x + 10y\)厘米 。
所以,这个长方形的周长是\((10x + 10y)\)厘米 。
五、易错点分析
去括号时符号错误:当括号前是 “\(-\)” 号,容易忘记改变原括号里各项的符号;当括号前是数字因数时,可能出现乘法分配律使用错误,没有将数字因数与括号内的每一项都相乘 。例如在计算\(2 - (3x - 1)\)时,错误地得到\(2 - 3x - 1\),正确的应该是\(2 - 3x + 1\);计算\(2(3x + 2)\)时,错误写成\(6x + 2\),正确结果是\(6x + 4\) 。
合并同类项错误:找错同类项或者在合并同类项时,错误地对字母或字母的指数进行了运算 。比如把\(3x^2\)与\(3x\)当作同类项合并,或者在合并\(2x^2 + 3x^2\)时,错误地得到\(5x^4\) 。
运算顺序错误:在整式加减法中,有括号的要先去括号,再合并同类项。如果没有按照正确的顺序进行运算,就会得到错误的结果 。例如对于式子\((2x + 3) - (x - 1) + 2x\),如果先计算\(2x + 3 - x\),就会出现错误,应该先去括号得到\(2x + 3 - x + 1 + 2x\),再合并同类项 。
通过以上对整式的加法与减法的学习,我们了解了其运算的基础、概念、步骤、应用以及易错点。在实际运算过程中,要认真仔细,准确运用去括号法则和合并同类项的方法,提高运算的准确性。如果还有任何疑问,欢迎随时探讨。
这份内容围绕整式加减法展开,从基础到应用逐步深入。若你觉得某些部分讲解不够详细,或想增加特定类型例题,欢迎提出,我们一起优化。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
复习导入
合并同类项:系数相加,字母及其指数不变.
去括号:括号前是“+”号,去括号后括号里各项不变号.
去括号:括号前是“-”号,去括号后括号里各项都变号.
5x+2x-4x= _________= _________ .
x+(a-b) = _________.
x- (a-b) = _________.
(5+2-4)x
3x
x+a-b
x-a+b
去括号依据:乘法分配律:a (b+c) = ab+ac
选择题
1.下列去括号,正确的是 ( )
A. a-(b+c)=a-b-c B. a+(b-c)=a+b+c
C. a-(b+c)=a-b+c D. a-(b+c)=a+b-c
2.在 -( )=-x2+3x-2 的括号里应填上的代数式是 ( )
A. x2-3x-2 B. x2+3x-2
C. x2-3x+2 D. x2+3x+2
3.下列各式中与多项式 2x-3y+4z 相等的是 ( )
A.2x+(3y-4z) B. 2x-(3y-4z)
C. 2x+(3y+4z) D. 2x-(3y+4z)
A
C
B
探索新知
思 考
计算:3(xy-2y)-5(x-2y+1)=____________.
规定:整式的加法满足乘法对加法的分配律.
3(xy-2y)-5(x-2y+1)
= (3xy-6y)-(5x-10y+5)
= 3xy__6y__5x__10y__5
= 3xy-5x+4y-5 .
3xy-5x+4y-5
乘法对加法的分配律
去括号
合并同类项
-
-
+
-
结果为整式
例3
计算:(3x2y3-xy2)-2(x2y3+6xy2)+(-4x2y3+ 2xy2).
(3x2y3-xy2)-2(x2y3+6xy2)+(-4x2y3+ 2xy2)
解
=3x2y3-xy2-(2x2y3+12xy2)-4x2y3+ 2xy2
=3x2y3-xy2-2x2y3-12xy2-4x2y3+2xy2
=[3+(-2) +(-4)]x2y3 +[(-1)+(-12) +2]xy2
=-3x2y3-11xy2 .
去括号和合并同类项是整式的加减运算的基础.
“整式的加减”的一般步骤为:
①有括号,根据去括号法则去括号;
②找同类项,按照合并同类项法则合并同类项.
整式的加减运算的结果仍为整式.
注意:整式的加减运算的结果要求最简,
也就是运算结果中不能再有同类项.
练一练
1.计算:
(1) 3(x+y)-5(x+y)+(x+y);
(2) 5(3x2-2y)-4(2x+3y2)+(3x2-2y)-3(2x+3y2).
(1) 3(x+y)-5(x+y)+(x+y)
= (3x+3y)-(5x+5y)+(x+y)
= 3x+3y -5x- 5y+x+y
= (3-5+1)x +(3-5+1)y
= -x -y
(1) 3(x+y)-5(x+y)+(x+y)
= (3-5+1)(x+y)
= -x -y
= -(x+y)
方法2:
练一练
1.计算:
(1) 3(x+y)-5(x+y)+(x+y);
(2) 5(3x2-2y)-4(2x+3y2)+(3x2-2y)-3(2x+3y2).
(2) 5(3x2-2y)-4(2x+3y2)+(3x2-2y)-3(2x+3y2)
= (15x2-10y)-(8x+12y2)+3x2-2y- (6x+9y2)
= 15x2-10y-8x-12y2+3x2-2y-6x-9y2
= (15+3)x2+[(-8)+(-6)]x+[(-12)+(-9)]y2+[(-10)+(-2)]y
= 18x2-14x-21y2-12y .
例4
计算:
(1) (4x2-5xy+3y2)-(3x2+2y2);
(2) [4×(-2)2-5×(-2)×3+3×32]-[3×(-2)2+2×32];
(3) [4×(-3)2-5×(-3)×c+3×c2]-[3×(-3)2+2×c2].
分析:将(2)与(1)进行比较,可以发现:将(1)中的字母 x,y 分别用-2,3代入即可得(2),于是只需将(1)的结果中的字母 x,y 分别用-2,3代入,即可得(2)的结果,这样能大大减少运算量.类似地,可以求得(3)的计算结果.
例4
计算:
解
(1) (4x2-5xy+3y2)-(3x2+2y2)
= 4x2-5xy+3y2-3x2-2y2
= x2-5xy+y2 .
①
(1) (4x2-5xy+3y2)-(3x2+2y2);
(2) [4×(-2)2-5×(-2)×3+3×32]-[3×(-2)2+2×32];
(3) [4×(-3)2-5×(-3)×c+3×c2]-[3×(-3)2+2×c2].
例4
计算:
(2) 将等式①中的x 用-2,y用3代入,则
= x2-5xy+y2 .
[4×(-2)2-5×(-2)×3+3×32]-[3×(-2)2+2×32]
= (-2)2-5×(-2)×3+32
= 4+30+9
= 43 .
(1) (4x2-5xy+3y2)-(3x2+2y2);
(2) [4×(-2)2-5×(-2)×3+3×32]-[3×(-2)2+2×32];
(3) [4×(-3)2-5×(-3)×c+3×c2]-[3×(-3)2+2×c2].
例4
计算:
(3) 将等式①中的 x 用-3,y用 c 代入,则
= x2-5xy+y2 .
[4×(-3)2-5×(-3)×c+3×c2]-[3×(-3)2+2×c2]
= (-3)2-5×(-3)×c+c2
= 9+15c+c2
(1) (4x2-5xy+3y2)-(3x2+2y2);
(2) [4×(-2)2-5×(-2)×3+3×32]-[3×(-2)2+2×32];
(3) [4×(-3)2-5×(-3)×c+3×c2]-[3×(-3)2+2×c2].
练一练
1.先计算 2(x3y2-5xy3+x)+(3xy3-2x)-3(x3y2-xy3+7x),
再利用所得结果计算:2×[(-1)3×(-2)2-5×(-1)×(-2)3+(-1)] +[3 ×(-1) ×(-2)3-2 ×(-1)]-3× [(-1) 3×(-2)2- (-1)×(-2)3+7 ×(-1)] .
2(x3y2-5xy3+x)+(3xy3-2x)-3(x3y2-xy3+7x)
=(2x3y2-10xy3+2x)+3xy3-2x- (3x3y2-3xy3+21x)
=2x3y2-10xy3+2x+3xy3-2x- 3x3y2+3xy3-21x
=-x3y2-4xy3-21x
将x=-1,y=-2代入上式结果得,
- (-1)3×(-2)2-4×(-1) ×(-2)3-21×(-1)=-7 .
解:
【课本P86 习题2.4第4题】
课堂练习
1.一个多项式加上 -2+x-x2 得到 x2-1 ,则这个多项式是_________.
2.多项式x2-3kxy-3y2+xy-8 化简后不含 xy 项 ,则k 为_________.
2x2-x+1
3.计算:
(1) (-3x2y2+5xy-y3)+3(7x2y2-xy+4y3);
(2) (x3+5x-1)-3(2x3-3x2)+(4x2-5x+6);
(3) 4(-2x3+4x)+(x3-5x2+1)-2(-x3+x);
(4) (x3y-3x2y2-x)+4(2x3y-x2y2)-3(-x3y+6x2y2) .
解:
(1) 18x2y2+2xy+11y3;
(2) -5x3+10x2+5;
(3) -5x3-5x2+14x+1;
(4) 12x3y-25x2y2-x .
【课本P85 练习题】
4.小王认为:代数式 x2+x(x+y)-2x2-xy 的值与x,y的取值无关,你认为呢?试说明理由.
解:无关.
x2+x(x+y)-2x2-xy
=x2+x2+xy-2x2-xy
=(1+1-2)x2+(1-1)xy
=0
1. 与 的和为( )
A
A. B.
C. D.
返回
2. 某同学在完成化简:
的过程中,具体步骤如下:
解:原式
.③
以上解题过程中,出现错误的步骤是( )
C
A. ① B. ② C. ③ D. ①②③
返回
3. [2025邵阳月考]下面是小芳做的一道多项式的加减运算
题,但她不小心把一滴墨水滴在了上面:
,阴影部分即为被墨水弄污的部分,那么阴影部
分应是( )
D
A. B. C. D.
返回
4.某客车上原有 人,中途有一半人下车,又上来若
干人,这时车上共有乘客 人,则上车乘客是_____
_________人.
返回
5. 已知,, 三个有理数在数轴上的位置
如图所示.化简: _______.
【点拨】因为,所以, ,
,所以 .
返回
6.化简:
(1) ;
【解】原式 .
(2) .
原式
.
返回
7.先化简,再求值:
,其中 ,
.
【解】原式
,
当, 时,
原式 .
返回
8. 一个三位数的百位数字为,十位数字为,个位数字为 ,
若把它的百位数字与个位数字对调得到一个新数.计算原数与
新数的差,则下列各数一定能整除这个差的是( )
A
A. 11 B. 7 C. 5 D. 2
【点拨】原数-新数 ,故选A.
返回
9. 某果园引入了 个采摘机器人,这些机器人被分为两组,
每组的工作效率不同.第一组有 个机器人,每个机器人平均8
秒采摘一个苹果;第二组包含剩余的机器人,每个机器人平
均6秒采摘一个苹果.同时,果园内还有10名熟练的采摘工人,
他们每个人平均5秒采摘一个苹果.机器人与工人同时工作1小
时,则这 个机器人比这10名工人多采摘的苹果个数是
( )
B
A. B.
C. D.
返回
10. 若,,则 可以表示
为( )
C
A. B. C. D.
【点拨】因为,所以 .
返回
11. 如图,在一个长方形中放入三个正
方形,边长分别为,, ,若要求出
右上角阴影部分周长与左下角阴影部分
周长的差,则只需知道,, 中哪个
量( )
C
A. B.
C. D. ,, 中任意一个
【点拨】设重叠部分的小长方形的长为 ,宽为
,则右上角阴影部
,所以右上角阴影部分周长为 ,左下角阴影部分周长为
分周长与左下角阴影部分周长的差可表示为.所以只需知道,,中的 即可.
返回
12. 在数学中,为了书写简便,18世纪数学家
欧拉就引进了求和符号“ ”.如
,
,
.若
,则常数, 的值分别
是_________.
,54
【点拨】因为
,所以易知 ,所以
,所以
,即 ,所以
, .
返回
13. 定义新运算: .例如:
.
(1)计算: ,并写出其结果的次数和
项数;
【解】原式
.
的次数为2,项数为3.
(2)若与 互为相反数,求(1)中结果
的值.
因为与 互为相反数,
所以 ,
所以, ,
所以, ,
所以(1)中原式
.
返回
课堂小结
整式的加减
步骤
应用
去括号
合并同类项
谢谢观看!
同课章节目录
