3.4.2一元一次方程的应用(二) 课件(共39张PPT)
文档属性
| 名称 | 3.4.2一元一次方程的应用(二) 课件(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 06:57:41 | ||
图片预览











文档简介
(共39张PPT)
3.4.2一元一次方程的应用(二)
第3章 一次方程(组)
【2024新教材】湘教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
一元一次方程的应用(二)
在《一元一次方程的应用(一)》中,我们学习了和差倍分、行程、工程等常见问题的在实际生活与数学学习里,还有许多复杂且具有代表性的问题也能借助一元一次方程解决。接下来,我们继续探索更多类型的实际问题,进一步提升运用一元一次方程解决问题的能力。
一、销售利润问题
(一)基本概念与公式
成本:商家购进商品所花费的费用 。
售价:商家出售商品时的价格 。
利润:利润 = 售价 - 成本 。
利润率:利润率 = \(\frac{利润}{成本}×100\%\),由此可推导出利润 = 成本 × 利润率,售价 = 成本 ×(1 + 利润率) 。
(二)解题关键
理清成本、售价、利润、利润率之间的关系,找到题目中的等量关系,通常可根据利润或售价的不同表述来列方程 。
(三)示例讲解
例 1:某商店将某种服装按进价提高\(40\%\)后标价,又以八折优惠卖出,结果每件仍获利\(15\)元,这种服装每件的进价是多少元?
分析:设这种服装每件的进价是\(x\)元。进价提高\(40\%\)后的标价为\((1 + 40\%)x\)元,八折优惠后的售价为\((1 + 40\%)x 0.8\)元,利润为\(15\)元。根据 “售价 - 进价 = 利润” 这一等量关系列方程。
列方程:\((1 + 40\%)x 0.8 - x = 15\) 。
解方程:\(
\begin{align*}
1.4x 0.8 - x &= 15\\
1.12x - x &= 15\\
0.12x &= 15\\
x &= 15 ·0.12\\
x &= 125
\end{align*}
\)
检验与作答:将\(x = 125\)代入原方程,左边\(=(1 + 40\%) 125 0.8 - 125 = 1.4 125 0.8 - 125 = 140 - 125 = 15\),右边\(= 15\),左边等于右边,所以\(x = 125\)是原方程的解,即这种服装每件的进价是\(125\)元。
二、储蓄利息问题
(一)基本概念与公式
本金:存入银行的钱 。
利息:取款时银行多支付的钱 。利息 = 本金 × 利率 × 存期 。
本息和:本金与利息的总和,本息和 = 本金 + 利息 = 本金 ×(1 + 利率 × 存期) 。
(二)解题关键
明确本金、利息、利率、存期、本息和之间的数量关系,依据题目条件找出合适的等量关系列方程 。
(三)示例讲解
例 2:小明将\(2000\)元存入银行,定期一年,到期后取出本金和利息共\(2036\)元,求该存款的年利率是多少?
分析:设该存款的年利率是\(x\)。本金是\(2000\)元,存期\(1\)年,根据利息公式,利息为\(2000x 1\)元,本息和为\(2036\)元。根据 “本息和 = 本金 + 利息” 列方程。
列方程:\(2000 + 2000x 1 = 2036\) 。
解方程:\(
\begin{align*}
2000 + 2000x &= 2036\\
2000x &= 2036 - 2000\\
2000x &= 36\\
x &= 36 ·2000\\
x &= 0.018\\
x &= 1.8\%
\end{align*}
\)
检验与作答:将\(x = 1.8\%\)代入原方程,左边\(= 2000 + 2000 1.8\% 1 = 2000 + 36 = 2036\),右边\(= 2036\),左边等于右边,所以\(x = 1.8\%\)是原方程的解,即该存款的年利率是\(1.8\%\)。
三、配套生产问题
(一)问题特点
这类问题通常涉及两种或多种零件的生产,且零件之间存在一定的配套比例关系 。例如,一个桌子需要\(1\)个桌面和\(4\)条桌腿配套,生产时就要考虑桌面和桌腿数量的匹配。
(二)解题关键
根据配套比例关系,找出生产不同零件数量之间的等量关系,设未知数时可设生产其中一种零件的数量为\(x\),再根据比例表示出其他零件的数量,进而列出方程 。
(三)示例讲解
例 3:某车间有\(28\)名工人,生产一种螺栓和螺母,每人每天平均能生产螺栓\(12\)个或螺母\(18\)个,一个螺栓要配两个螺母。为了使每天生产的螺栓和螺母刚好配套,应安排多少名工人生产螺栓,多少名工人生产螺母?
分析:设应安排\(x\)名工人生产螺栓,则有\((28 - x)\)名工人生产螺母。每天生产螺栓的数量为\(12x\)个,生产螺母的数量为\(18 (28 - x)\)个。因为一个螺栓配两个螺母,所以螺母数量是螺栓数量的\(2\)倍,根据这一等量关系列方程。
列方程:\(2 12x = 18 (28 - x)\) 。
解方程:\(
\begin{align*}
24x &= 18 28 - 18x\\
24x + 18x &= 18 28\\
42x &= 504\\
x &= 504 ·42\\
x &= 12
\end{align*}
\)
求出答案:生产螺栓的工人有\(12\)名,生产螺母的工人有\(28 - 12 = 16\)名。
检验:生产螺栓的数量为\(12 12 = 144\)个,生产螺母的数量为\(18 16 = 288\)个,\(288 ·144 = 2\),螺母数量是螺栓数量的\(2\)倍,符合配套要求,所以答案正确。
通过对销售利润、储蓄利息、配套生产等问题的学习,我们进一步拓宽了一元一次方程的应用领域。在面对实际问题时,要深入分析问题本质,准确找到等量关系,灵活运用所学知识列出方程求解。后续还会有更多有趣且具有挑战性的应用问题等待我们去探索和解决。
以上内容介绍了新类型的一元一次方程应用问题。若你希望增加更多例题,或对某些问题的讲解方式有新想法,比如增加图表辅助理解,欢迎随时和我说。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
情境导入
甲、乙两车分别从A、B两地同时出发,相向而行,甲速度为20 km/h,乙速度为30 km/h,出发 x小时后,两人相遇.
那么甲车行了______km,乙车行了______km
A、B两地相距_________km.若A、B两站间的路程为500km,可得方程______________,求得x=____.
20x
30x
20x+30x
20x+30x=500
10
为进一步感悟雷锋胸怀祖国、服务人民的爱国精神,星期日早晨,小楠和小华分别骑自行车从家里同时出发去参观雷锋纪念馆.
探索新知
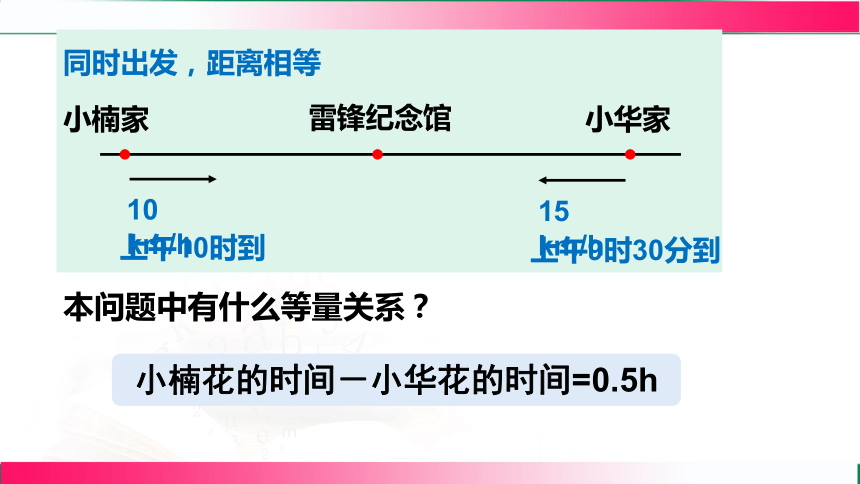
已知他俩的家到雷锋纪念馆的路程相等,并且小楠每小时骑10km,他在上午10时到达,小华每小时骑15km,他在上午9时30分到达. 他俩的家到雷锋纪念馆的路程是多少?
思 考
小楠家
小华家
雷锋纪念馆
同时出发,距离相等
10 km/h
上午10时到
15 km/h
上午9时30分到
本问题中有什么等量关系?
小楠花的时间-小华花的时间=0.5h
若设他俩的家到雷锋纪念馆的路程为 x km,
则根据等量关系,得
解得 x=15 .
因此,他俩的家到雷锋纪念馆的路程为15 km.
时间=路程÷速度
路程=时间×速度
小楠花的时间-小华花的时间=0.5h
应用一元一次方程解决问题的步骤:
1. 审:审题,分析题目中的数量关系;
2. 设:设适当的未知数,并表示未知量;
3. 列:根据题目中的数量关系列方程;
4. 解:解这个方程;
5. 答:检验并作答.
某人骑自行车去工厂上班,若每小时骑10 km,可早到6 min ;若每小时骑 8 km,就迟到6 min,则他家到工厂的路程是_______.
练一练
8 km
某校七年级甲班有45人,乙班有39人. 现要从甲、乙两班各抽调一些同学去参加“歌唱祖国”歌咏比赛,已知从甲班抽调的人比乙班多1人,此时甲班剩余人数恰好是乙班剩余人数的2倍. 请问:从甲、乙两班各抽调了多少人参加歌咏比赛?
分析:本题中的等量关系:
(1)甲班抽调的人数-乙班抽调的人数=1;
(2)抽调后甲班剩余人数=乙班剩余人数×2 .
例3
解:设从甲班抽调了x人,那么从乙班抽调了(x-1)人.
根据题意,得 45-x=2[39-(x-1)].
解得 x=35 .
于是,x-1=35-1=34 .
答:从甲班抽调了35人,从乙班抽调了34人参加歌咏比赛.
某校七年级甲班有45人,乙班有39人. 现要从甲、乙两班各抽调一些同学去参加“歌唱祖国”歌咏比赛,已知从甲班抽调的人比乙班多1人,此时甲班剩余人数恰好是乙班剩余人数的2倍. 请问:从甲、乙两班各抽调了多少人参加歌咏比赛?
例3
某班部分同学周日到公园游玩,休息时发现路边有若干条长凳,如果每3个同学坐一条长凳,则刚好还剩下一条长凳无人坐;如果每2个同学坐一条长凳,则还剩3个同学没有凳子坐. 路边共有多少条长凳
解:设路边共有x条长凳. 根据题意,得
3(x-1)=2x+3 ,
解得 x=6 .
答:路边共有6条长凳.
练一练
例4
现有树苗若干棵,计划栽在一段公路的一侧,
公路的两端各栽1棵,并且相邻两棵树的间隔相等.
方案一:如果每隔5m栽1棵,则树苗缺21棵;
方案二:如果每隔5.5m栽1棵,则树苗正好用完.
根据以上方案,请算出原有树苗的棵数和这段路的长度.
观察下面植树示意图,想一想:
相邻两树的间隔长、应植树棵数与路长有怎样的数量关系?
路长=相邻两树的间隔×(种植的树苗数-1)
设原有树苗x棵,由题意可得下表:
方案 间隔/m 种植的树苗数 路长/m
一 5
二 5.5
x+21
5(x+21-1)
x
5.5(x-1)
方案一和方案二的路长相等吗?
设原有树苗x棵,由题意可得下表:
方案 间隔/m 种植的树苗数 路长/m
一 5 x+21 5(x+21-1)
二 5.5 x 5.5(x-1)
解:设原有树苗x棵,根据题意,得
5(x+21-1)=5.5(x-1) .
解得 x = 211.
因此,原有树苗211棵,这段公路长为
5×(211+21-1)=5×231=1155(m) .
答:原有树苗211棵,这段公路长1155m.
相等
练一练
1.在一个圆形花坛的外围种植长春花,若每隔0.5 m种植1株,最后还剩3株;若每隔0.4 m种植1株,还需要购置12株,则原有长春花_____株.
63
2.绿化环境,美化生活. 现有树苗若干棵,计划栽在一段公路的一侧,要求路的两端各栽1棵.若每隔2m栽1棵,则树苗缺150棵;若每隔3m栽1棵,则树苗多出50棵. 求这段公路的长.
解:设这段公路的长为x m. 根据题意,得
解得 x=1 200.
答:这段公路的长为1200 m.
课堂练习
1.一队学生步行去参加社会公益活动,每小时走4km,学生甲因故推迟30 min 出发,为赶上队伍,甲以6 km/h的速度追赶,试问:甲用多长时间就可追上队伍
解:设甲用t h就可追上队伍,根据等量关系,得
4(0.5+t)=6t
解得 t=1
答:甲用1 h就可追上队伍.
【课本P115 练习 第1题】
2. 某村一条道路一侧装有路灯56盏(两端都有),且相邻两盏灯的距离为30m. 为进一步建设美丽乡村,该村计划将该道路的路灯全部更换为亮度更强的节能灯,且相邻两盏灯的距离变为25m,则需要安装节能灯多少盏?
路长=相邻两灯的间隔×(路灯的数量-1)
本问题中有什么等量关系?
【课本P115 练习 第2题】
解:设需要安装节能灯x盏,根据等量关系,得
25×(x-1)=30×(56-1)
解得 x=67
答:需要安装节能灯67盏.
路长=相邻两灯的间隔×(路灯的数量-1)
3.甲、乙两列火车从相距480 km的A,B两地同时出发,相向而行,甲火车每小时行驶120 km,乙火车每小时行驶100 km,经过多长时间两列火车相距40 km?
应用1 行程问题
1. 我国古代数学著作《九章算术》中有这样
一个问题:今有凫起南海,七日至北海.雁起北海,九日至南
海.今凫雁俱起.问:何日相逢?其大意为:野鸭从南海飞到
北海用7天,大雁从北海飞到南海用9天.它们从两地同时起飞,
几天后相遇?设 天后相遇,根据题意可列方程为_________
____.
返回
2. 如图,已知正方形 的边长为4,甲、
乙两动点分别从正方形的顶点,
同时出发,沿正方形的边开始移动,甲以
顺时针方向环行移动,乙以逆时针方向环
行移动,若乙的速度是甲的速度的3倍,
则它们第2 028次相遇时所在的边是( )
A
A. B. C. D.
返回
3.一列火车匀速行驶,经过一条长的隧道需要 的时
间.隧道的顶上有一盏灯,垂直向下发光,灯光照在火车上的
时间是.设火车长 ,解答下列问题.
(1)从车头经过灯下到车尾经过灯下,火车所走的路程是___
,这段时间内火车的速度是___.(用含 的代数式表示)
(2)从车头进入隧道到车尾离开隧道,火车所走的路程是
__________,这段时间内火车的速度是______ .
(用含 的代数式表示)
(3)求这列火车的长度.
【解】根据题意,得 ,
解得 .
答:这列火车的长度是 .
返回
4. 随着人们生活水平的提高,人工智能扫
地机器人成为上班族或现代家庭的常用家电.为了测试两款扫
地机器人的清扫速度,现安排甲、乙两个不同的扫地机器人
从, 两地同时出发,沿同一条路线相向匀速行驶清扫
(路途中没有障碍物阻挡),已知出发后经3分钟两个扫地
机器人相遇,相遇后再经2分钟乙到达地,, 两地相距
45米.
(1)甲、乙两个扫地机器人的速度分别是多少?
【解】根据题意,得乙扫地机器人的速度为
(米/分).
设甲扫地机器人的速度为米/分,则 ,解得
.
答:甲扫地机器人的速度为6米/分,乙扫地机器人的速度为9
米/分.
(2)从, 两地同时出发后,经过多长时间后两个扫地机
器人相距6米?
【解】设经过 分钟后两个扫地机器人相距6米.
当两个扫地机器人相遇前相距6米时,则 ,
解得 ;
当两个扫地机器人相遇后相距6米时,则 ,
解得 .
综上,经过或 分钟后两个扫地机器人相距6米.
返回
5.台州西站到永康南站现有一条设计时速为 的单轨普
速铁路.客车以 的平均速度行驶,从“铁路12306”可
查得它在各站点的到达时间和驶出时间如下表:
到达站点 临海南 仙居南 磐安南 壶镇 永康南
到达时间 11:03 11:25 11:53 12:04 12:23
驶出时间 11:05 11:27 11:55 12:07
(1)求临海南、仙居南、磐安南、壶镇相邻两站之间的铁
路长度.
【解】客车的行驶速度为 .
易知临海南到仙居南的铁路长度: ,
仙居南到磐安南的铁路长度: ,
磐安南到壶镇的铁路长度: .
(2)一列货车以 的速度匀速行驶开往永康南站,
在10:55通过临海南站.
货车的速度为 .
①若货车中途不停靠站点进行避让,它在到达永康南站前与
客车有追尾危险吗?如果有追尾危险,请确定在它驶离临海
南站多少千米时会追尾.
【解】首先判断到终点永康南站前,客车是否与货车有追尾
危险.由题意可得,以临海南站为起点,客车比货车晚
出发,壶镇到永康南的铁路长度为 ,所以
临海南至永康南的铁路总长度为
货车行驶时间为 ;
客车行驶时间为 ,易知三站停车总时
长为 .
因为 ,所以客车比货车
早到永康南,但时间很接近,所以两车有追尾危险,猜测两
车在壶镇至永康南段有追尾危险.
验证:假设两车在壶镇至永康南段追尾,设此时货车的行驶
时间为.根据题意可知 ,解
得,所以在货车驶离临海南站 时会
追尾.
②为确保列车运行安全,货车需要在客车追上前进入火车站,
停靠在货车等待轨道等待客车通过.则该货车应该停靠在
________站等待客车通过能使等待的时间最少.且停靠等待的
时间为___.精确到 .
磐安南
3
【点拨】若货车不等待客车先通过,两车在壶镇至永康南段
将会追尾.为避免两车追尾,货车可以停靠在仙居南站、磐安
南站或壶镇站等待客车先通过.
停仙居南站: ,货车等待时间为
,所以货车停仙居南站等待客车通过
要 .
停磐安南站: ,
,所以货车停磐安南站等待客车
通过约要 .
停壶镇站: ,
,所以货车停壶镇站等待客车
通过约要 .
综上所述,货车停靠在磐安南站等待的时间最少,最少为
.
返回
课堂小结
应用一元一次方程解决问题的步骤:
1. 审:审题,分析题目中的数量关系;
2. 设:设适当的未知数,并表示未知量;
3. 列:根据题目中的数量关系列方程;
4. 解:解这个方程;
5. 答:检验并作答.
谢谢观看!
3.4.2一元一次方程的应用(二)
第3章 一次方程(组)
【2024新教材】湘教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
一元一次方程的应用(二)
在《一元一次方程的应用(一)》中,我们学习了和差倍分、行程、工程等常见问题的在实际生活与数学学习里,还有许多复杂且具有代表性的问题也能借助一元一次方程解决。接下来,我们继续探索更多类型的实际问题,进一步提升运用一元一次方程解决问题的能力。
一、销售利润问题
(一)基本概念与公式
成本:商家购进商品所花费的费用 。
售价:商家出售商品时的价格 。
利润:利润 = 售价 - 成本 。
利润率:利润率 = \(\frac{利润}{成本}×100\%\),由此可推导出利润 = 成本 × 利润率,售价 = 成本 ×(1 + 利润率) 。
(二)解题关键
理清成本、售价、利润、利润率之间的关系,找到题目中的等量关系,通常可根据利润或售价的不同表述来列方程 。
(三)示例讲解
例 1:某商店将某种服装按进价提高\(40\%\)后标价,又以八折优惠卖出,结果每件仍获利\(15\)元,这种服装每件的进价是多少元?
分析:设这种服装每件的进价是\(x\)元。进价提高\(40\%\)后的标价为\((1 + 40\%)x\)元,八折优惠后的售价为\((1 + 40\%)x 0.8\)元,利润为\(15\)元。根据 “售价 - 进价 = 利润” 这一等量关系列方程。
列方程:\((1 + 40\%)x 0.8 - x = 15\) 。
解方程:\(
\begin{align*}
1.4x 0.8 - x &= 15\\
1.12x - x &= 15\\
0.12x &= 15\\
x &= 15 ·0.12\\
x &= 125
\end{align*}
\)
检验与作答:将\(x = 125\)代入原方程,左边\(=(1 + 40\%) 125 0.8 - 125 = 1.4 125 0.8 - 125 = 140 - 125 = 15\),右边\(= 15\),左边等于右边,所以\(x = 125\)是原方程的解,即这种服装每件的进价是\(125\)元。
二、储蓄利息问题
(一)基本概念与公式
本金:存入银行的钱 。
利息:取款时银行多支付的钱 。利息 = 本金 × 利率 × 存期 。
本息和:本金与利息的总和,本息和 = 本金 + 利息 = 本金 ×(1 + 利率 × 存期) 。
(二)解题关键
明确本金、利息、利率、存期、本息和之间的数量关系,依据题目条件找出合适的等量关系列方程 。
(三)示例讲解
例 2:小明将\(2000\)元存入银行,定期一年,到期后取出本金和利息共\(2036\)元,求该存款的年利率是多少?
分析:设该存款的年利率是\(x\)。本金是\(2000\)元,存期\(1\)年,根据利息公式,利息为\(2000x 1\)元,本息和为\(2036\)元。根据 “本息和 = 本金 + 利息” 列方程。
列方程:\(2000 + 2000x 1 = 2036\) 。
解方程:\(
\begin{align*}
2000 + 2000x &= 2036\\
2000x &= 2036 - 2000\\
2000x &= 36\\
x &= 36 ·2000\\
x &= 0.018\\
x &= 1.8\%
\end{align*}
\)
检验与作答:将\(x = 1.8\%\)代入原方程,左边\(= 2000 + 2000 1.8\% 1 = 2000 + 36 = 2036\),右边\(= 2036\),左边等于右边,所以\(x = 1.8\%\)是原方程的解,即该存款的年利率是\(1.8\%\)。
三、配套生产问题
(一)问题特点
这类问题通常涉及两种或多种零件的生产,且零件之间存在一定的配套比例关系 。例如,一个桌子需要\(1\)个桌面和\(4\)条桌腿配套,生产时就要考虑桌面和桌腿数量的匹配。
(二)解题关键
根据配套比例关系,找出生产不同零件数量之间的等量关系,设未知数时可设生产其中一种零件的数量为\(x\),再根据比例表示出其他零件的数量,进而列出方程 。
(三)示例讲解
例 3:某车间有\(28\)名工人,生产一种螺栓和螺母,每人每天平均能生产螺栓\(12\)个或螺母\(18\)个,一个螺栓要配两个螺母。为了使每天生产的螺栓和螺母刚好配套,应安排多少名工人生产螺栓,多少名工人生产螺母?
分析:设应安排\(x\)名工人生产螺栓,则有\((28 - x)\)名工人生产螺母。每天生产螺栓的数量为\(12x\)个,生产螺母的数量为\(18 (28 - x)\)个。因为一个螺栓配两个螺母,所以螺母数量是螺栓数量的\(2\)倍,根据这一等量关系列方程。
列方程:\(2 12x = 18 (28 - x)\) 。
解方程:\(
\begin{align*}
24x &= 18 28 - 18x\\
24x + 18x &= 18 28\\
42x &= 504\\
x &= 504 ·42\\
x &= 12
\end{align*}
\)
求出答案:生产螺栓的工人有\(12\)名,生产螺母的工人有\(28 - 12 = 16\)名。
检验:生产螺栓的数量为\(12 12 = 144\)个,生产螺母的数量为\(18 16 = 288\)个,\(288 ·144 = 2\),螺母数量是螺栓数量的\(2\)倍,符合配套要求,所以答案正确。
通过对销售利润、储蓄利息、配套生产等问题的学习,我们进一步拓宽了一元一次方程的应用领域。在面对实际问题时,要深入分析问题本质,准确找到等量关系,灵活运用所学知识列出方程求解。后续还会有更多有趣且具有挑战性的应用问题等待我们去探索和解决。
以上内容介绍了新类型的一元一次方程应用问题。若你希望增加更多例题,或对某些问题的讲解方式有新想法,比如增加图表辅助理解,欢迎随时和我说。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
情境导入
甲、乙两车分别从A、B两地同时出发,相向而行,甲速度为20 km/h,乙速度为30 km/h,出发 x小时后,两人相遇.
那么甲车行了______km,乙车行了______km
A、B两地相距_________km.若A、B两站间的路程为500km,可得方程______________,求得x=____.
20x
30x
20x+30x
20x+30x=500
10
为进一步感悟雷锋胸怀祖国、服务人民的爱国精神,星期日早晨,小楠和小华分别骑自行车从家里同时出发去参观雷锋纪念馆.
探索新知
已知他俩的家到雷锋纪念馆的路程相等,并且小楠每小时骑10km,他在上午10时到达,小华每小时骑15km,他在上午9时30分到达. 他俩的家到雷锋纪念馆的路程是多少?
思 考
小楠家
小华家
雷锋纪念馆
同时出发,距离相等
10 km/h
上午10时到
15 km/h
上午9时30分到
本问题中有什么等量关系?
小楠花的时间-小华花的时间=0.5h
若设他俩的家到雷锋纪念馆的路程为 x km,
则根据等量关系,得
解得 x=15 .
因此,他俩的家到雷锋纪念馆的路程为15 km.
时间=路程÷速度
路程=时间×速度
小楠花的时间-小华花的时间=0.5h
应用一元一次方程解决问题的步骤:
1. 审:审题,分析题目中的数量关系;
2. 设:设适当的未知数,并表示未知量;
3. 列:根据题目中的数量关系列方程;
4. 解:解这个方程;
5. 答:检验并作答.
某人骑自行车去工厂上班,若每小时骑10 km,可早到6 min ;若每小时骑 8 km,就迟到6 min,则他家到工厂的路程是_______.
练一练
8 km
某校七年级甲班有45人,乙班有39人. 现要从甲、乙两班各抽调一些同学去参加“歌唱祖国”歌咏比赛,已知从甲班抽调的人比乙班多1人,此时甲班剩余人数恰好是乙班剩余人数的2倍. 请问:从甲、乙两班各抽调了多少人参加歌咏比赛?
分析:本题中的等量关系:
(1)甲班抽调的人数-乙班抽调的人数=1;
(2)抽调后甲班剩余人数=乙班剩余人数×2 .
例3
解:设从甲班抽调了x人,那么从乙班抽调了(x-1)人.
根据题意,得 45-x=2[39-(x-1)].
解得 x=35 .
于是,x-1=35-1=34 .
答:从甲班抽调了35人,从乙班抽调了34人参加歌咏比赛.
某校七年级甲班有45人,乙班有39人. 现要从甲、乙两班各抽调一些同学去参加“歌唱祖国”歌咏比赛,已知从甲班抽调的人比乙班多1人,此时甲班剩余人数恰好是乙班剩余人数的2倍. 请问:从甲、乙两班各抽调了多少人参加歌咏比赛?
例3
某班部分同学周日到公园游玩,休息时发现路边有若干条长凳,如果每3个同学坐一条长凳,则刚好还剩下一条长凳无人坐;如果每2个同学坐一条长凳,则还剩3个同学没有凳子坐. 路边共有多少条长凳
解:设路边共有x条长凳. 根据题意,得
3(x-1)=2x+3 ,
解得 x=6 .
答:路边共有6条长凳.
练一练
例4
现有树苗若干棵,计划栽在一段公路的一侧,
公路的两端各栽1棵,并且相邻两棵树的间隔相等.
方案一:如果每隔5m栽1棵,则树苗缺21棵;
方案二:如果每隔5.5m栽1棵,则树苗正好用完.
根据以上方案,请算出原有树苗的棵数和这段路的长度.
观察下面植树示意图,想一想:
相邻两树的间隔长、应植树棵数与路长有怎样的数量关系?
路长=相邻两树的间隔×(种植的树苗数-1)
设原有树苗x棵,由题意可得下表:
方案 间隔/m 种植的树苗数 路长/m
一 5
二 5.5
x+21
5(x+21-1)
x
5.5(x-1)
方案一和方案二的路长相等吗?
设原有树苗x棵,由题意可得下表:
方案 间隔/m 种植的树苗数 路长/m
一 5 x+21 5(x+21-1)
二 5.5 x 5.5(x-1)
解:设原有树苗x棵,根据题意,得
5(x+21-1)=5.5(x-1) .
解得 x = 211.
因此,原有树苗211棵,这段公路长为
5×(211+21-1)=5×231=1155(m) .
答:原有树苗211棵,这段公路长1155m.
相等
练一练
1.在一个圆形花坛的外围种植长春花,若每隔0.5 m种植1株,最后还剩3株;若每隔0.4 m种植1株,还需要购置12株,则原有长春花_____株.
63
2.绿化环境,美化生活. 现有树苗若干棵,计划栽在一段公路的一侧,要求路的两端各栽1棵.若每隔2m栽1棵,则树苗缺150棵;若每隔3m栽1棵,则树苗多出50棵. 求这段公路的长.
解:设这段公路的长为x m. 根据题意,得
解得 x=1 200.
答:这段公路的长为1200 m.
课堂练习
1.一队学生步行去参加社会公益活动,每小时走4km,学生甲因故推迟30 min 出发,为赶上队伍,甲以6 km/h的速度追赶,试问:甲用多长时间就可追上队伍
解:设甲用t h就可追上队伍,根据等量关系,得
4(0.5+t)=6t
解得 t=1
答:甲用1 h就可追上队伍.
【课本P115 练习 第1题】
2. 某村一条道路一侧装有路灯56盏(两端都有),且相邻两盏灯的距离为30m. 为进一步建设美丽乡村,该村计划将该道路的路灯全部更换为亮度更强的节能灯,且相邻两盏灯的距离变为25m,则需要安装节能灯多少盏?
路长=相邻两灯的间隔×(路灯的数量-1)
本问题中有什么等量关系?
【课本P115 练习 第2题】
解:设需要安装节能灯x盏,根据等量关系,得
25×(x-1)=30×(56-1)
解得 x=67
答:需要安装节能灯67盏.
路长=相邻两灯的间隔×(路灯的数量-1)
3.甲、乙两列火车从相距480 km的A,B两地同时出发,相向而行,甲火车每小时行驶120 km,乙火车每小时行驶100 km,经过多长时间两列火车相距40 km?
应用1 行程问题
1. 我国古代数学著作《九章算术》中有这样
一个问题:今有凫起南海,七日至北海.雁起北海,九日至南
海.今凫雁俱起.问:何日相逢?其大意为:野鸭从南海飞到
北海用7天,大雁从北海飞到南海用9天.它们从两地同时起飞,
几天后相遇?设 天后相遇,根据题意可列方程为_________
____.
返回
2. 如图,已知正方形 的边长为4,甲、
乙两动点分别从正方形的顶点,
同时出发,沿正方形的边开始移动,甲以
顺时针方向环行移动,乙以逆时针方向环
行移动,若乙的速度是甲的速度的3倍,
则它们第2 028次相遇时所在的边是( )
A
A. B. C. D.
返回
3.一列火车匀速行驶,经过一条长的隧道需要 的时
间.隧道的顶上有一盏灯,垂直向下发光,灯光照在火车上的
时间是.设火车长 ,解答下列问题.
(1)从车头经过灯下到车尾经过灯下,火车所走的路程是___
,这段时间内火车的速度是___.(用含 的代数式表示)
(2)从车头进入隧道到车尾离开隧道,火车所走的路程是
__________,这段时间内火车的速度是______ .
(用含 的代数式表示)
(3)求这列火车的长度.
【解】根据题意,得 ,
解得 .
答:这列火车的长度是 .
返回
4. 随着人们生活水平的提高,人工智能扫
地机器人成为上班族或现代家庭的常用家电.为了测试两款扫
地机器人的清扫速度,现安排甲、乙两个不同的扫地机器人
从, 两地同时出发,沿同一条路线相向匀速行驶清扫
(路途中没有障碍物阻挡),已知出发后经3分钟两个扫地
机器人相遇,相遇后再经2分钟乙到达地,, 两地相距
45米.
(1)甲、乙两个扫地机器人的速度分别是多少?
【解】根据题意,得乙扫地机器人的速度为
(米/分).
设甲扫地机器人的速度为米/分,则 ,解得
.
答:甲扫地机器人的速度为6米/分,乙扫地机器人的速度为9
米/分.
(2)从, 两地同时出发后,经过多长时间后两个扫地机
器人相距6米?
【解】设经过 分钟后两个扫地机器人相距6米.
当两个扫地机器人相遇前相距6米时,则 ,
解得 ;
当两个扫地机器人相遇后相距6米时,则 ,
解得 .
综上,经过或 分钟后两个扫地机器人相距6米.
返回
5.台州西站到永康南站现有一条设计时速为 的单轨普
速铁路.客车以 的平均速度行驶,从“铁路12306”可
查得它在各站点的到达时间和驶出时间如下表:
到达站点 临海南 仙居南 磐安南 壶镇 永康南
到达时间 11:03 11:25 11:53 12:04 12:23
驶出时间 11:05 11:27 11:55 12:07
(1)求临海南、仙居南、磐安南、壶镇相邻两站之间的铁
路长度.
【解】客车的行驶速度为 .
易知临海南到仙居南的铁路长度: ,
仙居南到磐安南的铁路长度: ,
磐安南到壶镇的铁路长度: .
(2)一列货车以 的速度匀速行驶开往永康南站,
在10:55通过临海南站.
货车的速度为 .
①若货车中途不停靠站点进行避让,它在到达永康南站前与
客车有追尾危险吗?如果有追尾危险,请确定在它驶离临海
南站多少千米时会追尾.
【解】首先判断到终点永康南站前,客车是否与货车有追尾
危险.由题意可得,以临海南站为起点,客车比货车晚
出发,壶镇到永康南的铁路长度为 ,所以
临海南至永康南的铁路总长度为
货车行驶时间为 ;
客车行驶时间为 ,易知三站停车总时
长为 .
因为 ,所以客车比货车
早到永康南,但时间很接近,所以两车有追尾危险,猜测两
车在壶镇至永康南段有追尾危险.
验证:假设两车在壶镇至永康南段追尾,设此时货车的行驶
时间为.根据题意可知 ,解
得,所以在货车驶离临海南站 时会
追尾.
②为确保列车运行安全,货车需要在客车追上前进入火车站,
停靠在货车等待轨道等待客车通过.则该货车应该停靠在
________站等待客车通过能使等待的时间最少.且停靠等待的
时间为___.精确到 .
磐安南
3
【点拨】若货车不等待客车先通过,两车在壶镇至永康南段
将会追尾.为避免两车追尾,货车可以停靠在仙居南站、磐安
南站或壶镇站等待客车先通过.
停仙居南站: ,货车等待时间为
,所以货车停仙居南站等待客车通过
要 .
停磐安南站: ,
,所以货车停磐安南站等待客车
通过约要 .
停壶镇站: ,
,所以货车停壶镇站等待客车
通过约要 .
综上所述,货车停靠在磐安南站等待的时间最少,最少为
.
返回
课堂小结
应用一元一次方程解决问题的步骤:
1. 审:审题,分析题目中的数量关系;
2. 设:设适当的未知数,并表示未知量;
3. 列:根据题目中的数量关系列方程;
4. 解:解这个方程;
5. 答:检验并作答.
谢谢观看!
同课章节目录
