4.3.2.1角的度量与计算 课件(共42张PPT)
文档属性
| 名称 | 4.3.2.1角的度量与计算 课件(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 32.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 07:58:23 | ||
图片预览







文档简介
(共42张PPT)
4.3.2.1角的度量与计算
第4章 图形的认识
【2024新教材】湘教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
角的度量与计算
在学习了角与角的大小比较后,我们进一步深入探究角的度量与计算。角的度量是量化角的大小的重要手段,而角的计算则能帮助我们解决更多复杂的几何问题,无论是在数学课堂上,还是在建筑、机械制造等实际领域,这部分知识都有着举足轻重的地位。
一、角的度量单位及换算
(一)基本度量单位
角的度量单位主要有度、分、秒,分别用符号 “\(^{\circ}\)”“\('\)”“\(''\)” 表示 。把一个周角\(360^{\circ}\)平均分成\(360\)等份,每一份就是\(1\)度的角,记作\(1^{\circ}\);把\(1^{\circ}\)的角平均分成\(60\)等份,每一份叫做\(1\)分的角,记作\(1'\);把\(1'\)的角再平均分成\(60\)等份,每一份叫做\(1\)秒的角,记作\(1''\) 。
(二)单位换算关系
度、分、秒之间的换算为六十进制,即\(1^{\circ}=60'\),\(1' = 60''\),由此可推导出\(1^{\circ}=3600''\) 。
从度换算到分或秒时,乘以相应的进率,例如将\(3.5^{\circ}\)换算成分,\(3.5^{\circ} = 3.5 60' = 210'\);将\(2^{\circ}\)换算成秒,\(2^{\circ}=2 3600'' = 7200''\) 。
从分或秒换算到度时,除以相应的进率,比如将\(180'\)换算成度,\(180' ·60 = 3^{\circ}\);将\(3600''\)换算成度,\(3600'' ·3600 = 1^{\circ}\) 。
二、量角器的使用
(一)认识量角器
量角器是度量角的大小的工具,它一般为半圆形,外圈刻度从\(0^{\circ}\)到\(180^{\circ}\)顺时针方向标注,内圈刻度从\(0^{\circ}\)到\(180^{\circ}\)逆时针方向标注,量角器的中心有一个小圆点 。
(二)使用步骤
点重合:把量角器的中心与角的顶点重合 。
线重合:将量角器的\(0^{\circ}\)刻度线与角的一条边重合 。这里要注意,如果角的一条边与外圈\(0^{\circ}\)刻度线重合,就读外圈刻度;若与内圈\(0^{\circ}\)刻度线重合,就读内圈刻度 。
读度数:角的另一条边所对的量角器上的刻度,就是这个角的度数 。例如,测量\(\angle ABC\),当顶点\(B\)与量角器中心重合,一条边\(BA\)与内圈\(0^{\circ}\)刻度线重合,另一条边\(BC\)指向内圈\(50^{\circ}\)刻度线,那么\(\angle ABC = 50^{\circ}\) 。
三、角的计算
(一)角度的加减计算
计算规则:度与度、分与分、秒与秒分别相加减 。如果分或秒的计算结果满\(60\),则要向上一级单位进\(1\);如果在减法运算中,分或秒不够减,需要从上一级单位借\(1\)当\(60\) 。
示例:
计算\(45^{\circ}30' + 30^{\circ}20'\):
度相加:\(45^{\circ} + 30^{\circ} = 75^{\circ}\);
分相加:\(30' + 20' = 50'\);
所以结果为\(75^{\circ}50'\) 。
计算\(60^{\circ} - 25^{\circ}40'\):
因为\(0' < 40'\),从\(60^{\circ}\)借\(1^{\circ}\),\(1^{\circ}=60'\),则\(60^{\circ}=59^{\circ}60'\);
度相减:\(59^{\circ} - 25^{\circ} = 34^{\circ}\);
分相减:\(60' - 40' = 20'\);
所以结果为\(34^{\circ}20'\) 。
(二)角度的乘法计算
计算规则:度、分、秒分别与乘数相乘,然后按照六十进制进行进位 。
示例:计算\(3 25^{\circ}15'\):
度相乘:\(3 25^{\circ} = 75^{\circ}\);
分相乘:\(3 15' = 45'\);
所以结果为\(75^{\circ}45'\) 。
(三)角度在几何图形中的计算
在几何图形中,常常需要根据已知角的度数,结合图形的性质来计算未知角的度数 。例如,在一个三角形中,已知两个内角分别为\(30^{\circ}\)和\(60^{\circ}\),根据三角形内角和为\(180^{\circ}\),可计算出第三个角的度数为\(180^{\circ} - 30^{\circ} - 60^{\circ} = 90^{\circ}\) 。再如,已知一个角的余角比它的补角的\(\frac{1}{3}\)还少\(20^{\circ}\),设这个角为\(x^{\circ}\),它的余角为\((90 - x)^{\circ}\),补角为\((180 - x)^{\circ}\),可列方程\(90 - x = \frac{1}{3}(180 - x) - 20\),求解方程就能得出这个角的度数 。
通过对 “角的度量与计算” 的学习,我们掌握了角的度量单位换算、量角器使用以及角度计算的方法。在学习过程中,要多做练习,尤其是涉及角度计算的实际问题和几何图形问题,加深对知识的理解和运用。如果在学习中有任何疑问,欢迎随时交流探讨,我们一起攻克学习难关。
上述内容全面介绍了角的度量与计算知识。若你觉得示例数量、讲解深度等方面需要调整,或者想补充特定类型的题目,欢迎随时和我说。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
问题导入
下面两个钟面上,时针与分针间的夹角谁大谁小呢
具体大多少?
如何去度量?
探索新知
把一个周角(即它的旋转量)分为 360 等份,每一等份叫作 1 度,记作 1°.
1度的概念
如何衡量一个角的大小
用量角器可以量出角的度数,那么、“1度”到底是多大呢
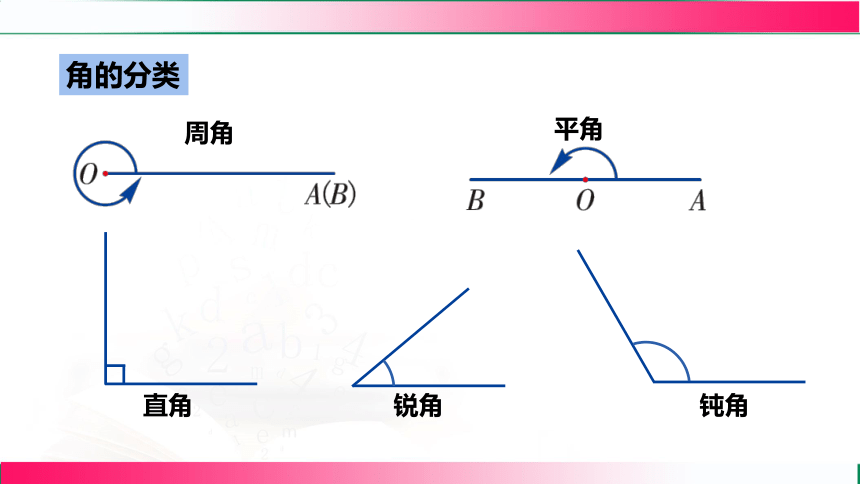
角的分类
周角
平角
直角
锐角
钝角
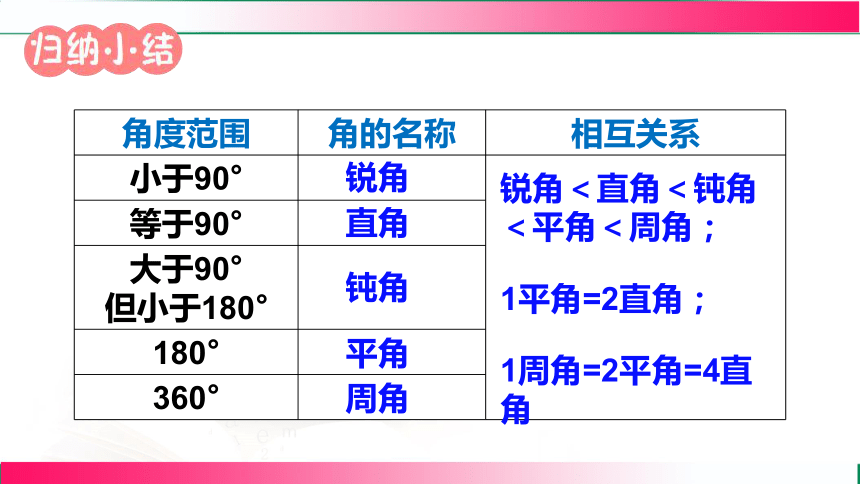
角度范围 角的名称 相互关系
小于90°
等于90° 大于90° 但小于180° 180° 360° 锐角
直角
钝角
平角
周角
锐角<直角<钝角<平角<周角;
1平角=2直角;
1周角=2平角=4直角
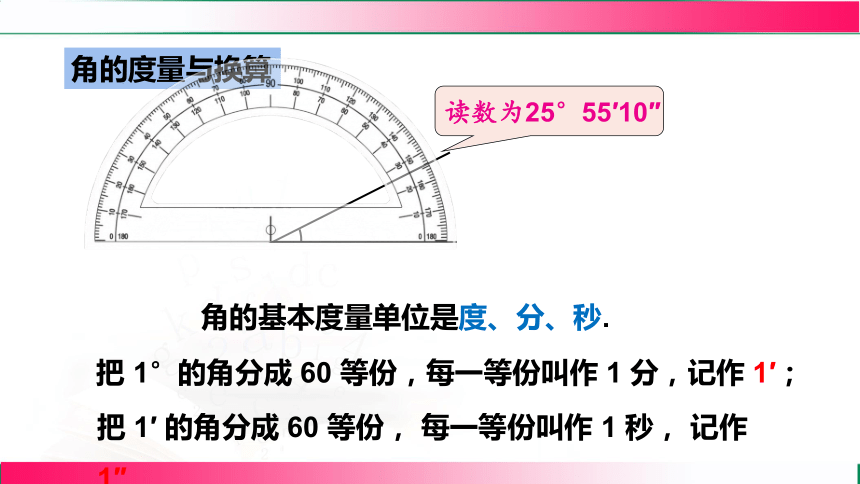
角的度量与换算
角的基本度量单位是度、分、秒.
把 1°的角分成 60 等份,每一等份叫作 1 分,记作 1′;
把 1′ 的角分成 60 等份, 每一等份叫作 1 秒, 记作 1″.
读数为25°55′10″
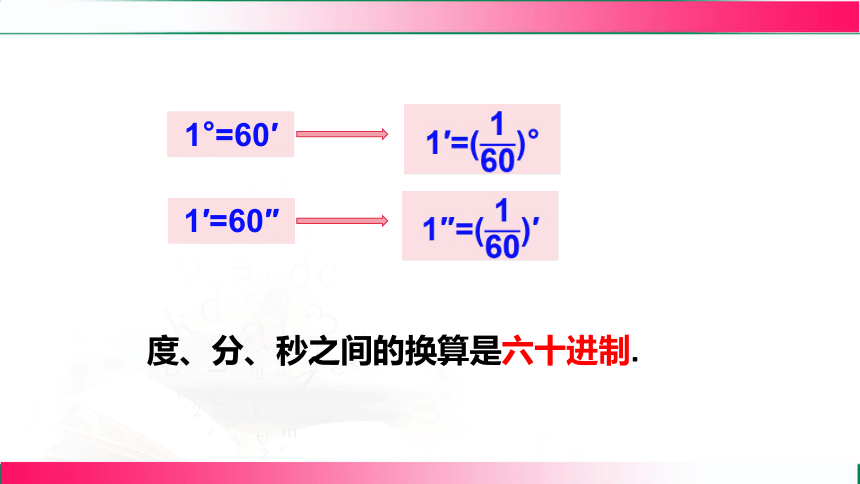
1°=60′
1′=60″
1′=()°
1″=()′
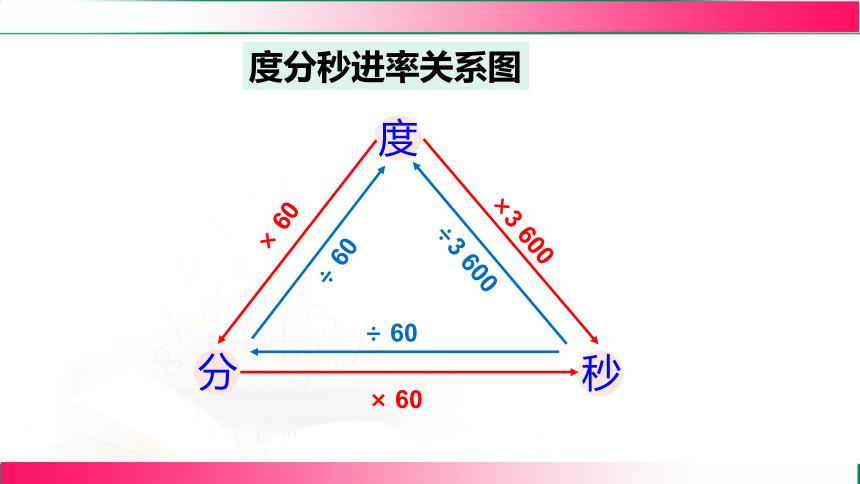
度、分、秒之间的换算是六十进制.
度
分
秒
× 60
×3 600
× 60
÷3 600
÷ 60
÷ 60
度分秒进率关系图
用度、分、秒表示 54.26°.
解 54.26°= 54°+ 0.26°.
又 0.26°= 0.26× 60′
= 15.6′ = 15′ + 0.6′,
而 0.6′ = 0.6 × 60″ = 36″,
因此,54.26°= 54°15′36″.
按1°=60′,1′=60″先把度化成分,再把分化成秒.
(小数化整数)
用度表示 48°25′48″.
解
因此,48°25′48″ = 48.43°.
按1″=(1/60)′,1′= (1/60)°,先把秒化成分,再把分化成度.
(整数化小数)
25′48″ = 25′+48″= 25′+ 0.8′= 25.8′,
计算:
(1) 把25.72°用度、分、秒的形式表示;
(2) 把45°12′30″化成度.
解: (1) ∵0.72°= 0.72× 60′=43.2′,
0.2× 60″=12″,
∴25.72°=25°43′12″
(2) ∵30″= 30× ()′=0.5′,
12.5× ()°≈0. 21°,
∴45°12′30″≈45. 21°
除不尽可以四舍五入取近似值
计算:
(1) 37°28′ + 24°35′; (2) 83°20′- 45°38′20″
解 (1) 37°28′+ 24°35′ = 61°63′ = 62°3′;
(2) 83°20′ - 45°38′20″
= 82°79′60″ - 45°38′20″
= 37°41′40″.
逢“60”进 “1”
不够减,向前一位借“1”
计算:
(1) 20°26′ + 30°54′; (2) 90°- 43°18′.
解 (1) 20°26′+ 35°54′
= 55°80′
= 56°20′;
(2) 90° -43°18′
= 89°60′- 43°18′
= 46°42′.
(1) 把度换算成度、分、秒:从左往右依次进行. 整数度保持不变,把不满 1 度的小数度化为分,再把不满 1 分的小数分化为秒,最后把度、分、秒合写在一起.
(2) 把度、分、秒换算成度:从右往左进行. 先把秒化为分,再把分化为度,最后把原来的度与由分和秒转化成的度相加.
角度单位之间的换算方法:
课堂练习
1. 下列算式正确的是( )
①33.33°=33°3′3″;
②33.33°=33°19′48″;
③50°40′33″=50.43°;
④50°40′30″=50.675°.
A. ①和②
B. ①和③
C. ②和③
D. ②和④
D
【教材P164页 练习第1题】
2. 填空:
(1) 0.65°= ′;
(2) 32.43°= ° ′ ″;
(3) 120°36′54″= °;
(4) 108°42′36″ = °.
39
32
25
48
120.615
108.71
4. 若∠C = 90°,∠A = 25°30′,则 ∠C-∠A 的结果是( )
A. 75°30′ B. 74°30′
C. 65°30′ D. 64°30′
D
3. 比较大小:74.45°_______ 74°45′
<
5. 计算:
(1) 72°12′ + 50°40′30″;
(2) 113°50′40″ - 57°48′42″.
122°52′30″
56°1′58″
【教材P164页 练习第2题】
6. 10 时整,钟表的时针与分针之间所成的角的度数是多少?15 时整呢?
答:10 时整,钟表的时针与分针之间所成的角度数为 60 度,15时整所成的角是 90 度.
【教材P164页 练习第3题】
7. 小红早晨8:30出发,中午12:30到家,则小红出发时时针和分针的夹角为_______,到家时时针和分针的夹角为_______.
75°
165°
解析:与12点整相比,8:30时,
时针转过了 (8+ )×30°=255°,
分针转过了 30×6°=180°,
所以夹角为255°-180°=75°.
同理12:30时,时针和分针的夹角为165°.
1. 若, ,
,则( )
A
A. B.
C. D.
返回
(第2题)
2. [2024广东]如图,一把直尺、
两个含 的三角尺拼接在一起,
则 的度数为( )
C
A. B.
C. D.
返回
3. 将与两个角的关系记为 ,下列探索
的大小与两个角的类型之间的关系中正确的是( )
A
A. 当时,若为锐角,则 为锐角
B. 当时,若为钝角,则 为钝角
C. 当时,若为锐角,则 为锐角
D. 当时,若为锐角,则 为钝角
返回
4. 当分针指向12,时针恰好与分针成
角时是( )
D
A. 9点钟 B. 8点钟
C. 4点钟 D. 8点钟或4点钟
【点拨】当分针指向12,与时
针的夹角为 时,有如图
两种情况,此时是8点钟或4点
钟,故选D.
返回
5. 用一副三角板可以画出一些角.在 , , ,
, , , , , , ,
的角中,能画出的角有( )
A
A. 11个 B. 10个
C. 9个 D. 8个
返回
6.将量角器按如图方式放置,其中角度为 的角是_______
________.
和
(第6题)
返回
7.计算:
(1) ;
【解】 .
(2) ;
.
(3) ;
.
(4) .
.
返回
8. 将一副三角尺按如图方式摆放,使三角尺的一个顶点重
合, , ,和分别是 和
的平分线.若 ,下列结论错误的是( )
D
A.
B.
C.
D.
【点拨】因为 ,
,和 分别是
和 的平分线,所以
,
.因为 ,所以
,
,
, .
返回
9.[2025长沙望城区模拟]如图,是直线上一点, 平
分,平分 .
(1)求出 的度数,你能得出什么结论?
【解】由角平分线的定义可知
, .
再由题图中角的关系得
,
所以 .
结论:的度数恒为 ,和射线 的位置无关.
(2)如果,求 的度数.
由(1)可得 ,所以 .
返回
课堂小结
角的度量与计算
角的分类
角的单位换算
借位
进位
角的和、差计算
大单位化成小单位
小单位化成大单位
谢谢观看!
4.3.2.1角的度量与计算
第4章 图形的认识
【2024新教材】湘教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
角的度量与计算
在学习了角与角的大小比较后,我们进一步深入探究角的度量与计算。角的度量是量化角的大小的重要手段,而角的计算则能帮助我们解决更多复杂的几何问题,无论是在数学课堂上,还是在建筑、机械制造等实际领域,这部分知识都有着举足轻重的地位。
一、角的度量单位及换算
(一)基本度量单位
角的度量单位主要有度、分、秒,分别用符号 “\(^{\circ}\)”“\('\)”“\(''\)” 表示 。把一个周角\(360^{\circ}\)平均分成\(360\)等份,每一份就是\(1\)度的角,记作\(1^{\circ}\);把\(1^{\circ}\)的角平均分成\(60\)等份,每一份叫做\(1\)分的角,记作\(1'\);把\(1'\)的角再平均分成\(60\)等份,每一份叫做\(1\)秒的角,记作\(1''\) 。
(二)单位换算关系
度、分、秒之间的换算为六十进制,即\(1^{\circ}=60'\),\(1' = 60''\),由此可推导出\(1^{\circ}=3600''\) 。
从度换算到分或秒时,乘以相应的进率,例如将\(3.5^{\circ}\)换算成分,\(3.5^{\circ} = 3.5 60' = 210'\);将\(2^{\circ}\)换算成秒,\(2^{\circ}=2 3600'' = 7200''\) 。
从分或秒换算到度时,除以相应的进率,比如将\(180'\)换算成度,\(180' ·60 = 3^{\circ}\);将\(3600''\)换算成度,\(3600'' ·3600 = 1^{\circ}\) 。
二、量角器的使用
(一)认识量角器
量角器是度量角的大小的工具,它一般为半圆形,外圈刻度从\(0^{\circ}\)到\(180^{\circ}\)顺时针方向标注,内圈刻度从\(0^{\circ}\)到\(180^{\circ}\)逆时针方向标注,量角器的中心有一个小圆点 。
(二)使用步骤
点重合:把量角器的中心与角的顶点重合 。
线重合:将量角器的\(0^{\circ}\)刻度线与角的一条边重合 。这里要注意,如果角的一条边与外圈\(0^{\circ}\)刻度线重合,就读外圈刻度;若与内圈\(0^{\circ}\)刻度线重合,就读内圈刻度 。
读度数:角的另一条边所对的量角器上的刻度,就是这个角的度数 。例如,测量\(\angle ABC\),当顶点\(B\)与量角器中心重合,一条边\(BA\)与内圈\(0^{\circ}\)刻度线重合,另一条边\(BC\)指向内圈\(50^{\circ}\)刻度线,那么\(\angle ABC = 50^{\circ}\) 。
三、角的计算
(一)角度的加减计算
计算规则:度与度、分与分、秒与秒分别相加减 。如果分或秒的计算结果满\(60\),则要向上一级单位进\(1\);如果在减法运算中,分或秒不够减,需要从上一级单位借\(1\)当\(60\) 。
示例:
计算\(45^{\circ}30' + 30^{\circ}20'\):
度相加:\(45^{\circ} + 30^{\circ} = 75^{\circ}\);
分相加:\(30' + 20' = 50'\);
所以结果为\(75^{\circ}50'\) 。
计算\(60^{\circ} - 25^{\circ}40'\):
因为\(0' < 40'\),从\(60^{\circ}\)借\(1^{\circ}\),\(1^{\circ}=60'\),则\(60^{\circ}=59^{\circ}60'\);
度相减:\(59^{\circ} - 25^{\circ} = 34^{\circ}\);
分相减:\(60' - 40' = 20'\);
所以结果为\(34^{\circ}20'\) 。
(二)角度的乘法计算
计算规则:度、分、秒分别与乘数相乘,然后按照六十进制进行进位 。
示例:计算\(3 25^{\circ}15'\):
度相乘:\(3 25^{\circ} = 75^{\circ}\);
分相乘:\(3 15' = 45'\);
所以结果为\(75^{\circ}45'\) 。
(三)角度在几何图形中的计算
在几何图形中,常常需要根据已知角的度数,结合图形的性质来计算未知角的度数 。例如,在一个三角形中,已知两个内角分别为\(30^{\circ}\)和\(60^{\circ}\),根据三角形内角和为\(180^{\circ}\),可计算出第三个角的度数为\(180^{\circ} - 30^{\circ} - 60^{\circ} = 90^{\circ}\) 。再如,已知一个角的余角比它的补角的\(\frac{1}{3}\)还少\(20^{\circ}\),设这个角为\(x^{\circ}\),它的余角为\((90 - x)^{\circ}\),补角为\((180 - x)^{\circ}\),可列方程\(90 - x = \frac{1}{3}(180 - x) - 20\),求解方程就能得出这个角的度数 。
通过对 “角的度量与计算” 的学习,我们掌握了角的度量单位换算、量角器使用以及角度计算的方法。在学习过程中,要多做练习,尤其是涉及角度计算的实际问题和几何图形问题,加深对知识的理解和运用。如果在学习中有任何疑问,欢迎随时交流探讨,我们一起攻克学习难关。
上述内容全面介绍了角的度量与计算知识。若你觉得示例数量、讲解深度等方面需要调整,或者想补充特定类型的题目,欢迎随时和我说。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
问题导入
下面两个钟面上,时针与分针间的夹角谁大谁小呢
具体大多少?
如何去度量?
探索新知
把一个周角(即它的旋转量)分为 360 等份,每一等份叫作 1 度,记作 1°.
1度的概念
如何衡量一个角的大小
用量角器可以量出角的度数,那么、“1度”到底是多大呢
角的分类
周角
平角
直角
锐角
钝角
角度范围 角的名称 相互关系
小于90°
等于90° 大于90° 但小于180° 180° 360° 锐角
直角
钝角
平角
周角
锐角<直角<钝角<平角<周角;
1平角=2直角;
1周角=2平角=4直角
角的度量与换算
角的基本度量单位是度、分、秒.
把 1°的角分成 60 等份,每一等份叫作 1 分,记作 1′;
把 1′ 的角分成 60 等份, 每一等份叫作 1 秒, 记作 1″.
读数为25°55′10″
1°=60′
1′=60″
1′=()°
1″=()′
度、分、秒之间的换算是六十进制.
度
分
秒
× 60
×3 600
× 60
÷3 600
÷ 60
÷ 60
度分秒进率关系图
用度、分、秒表示 54.26°.
解 54.26°= 54°+ 0.26°.
又 0.26°= 0.26× 60′
= 15.6′ = 15′ + 0.6′,
而 0.6′ = 0.6 × 60″ = 36″,
因此,54.26°= 54°15′36″.
按1°=60′,1′=60″先把度化成分,再把分化成秒.
(小数化整数)
用度表示 48°25′48″.
解
因此,48°25′48″ = 48.43°.
按1″=(1/60)′,1′= (1/60)°,先把秒化成分,再把分化成度.
(整数化小数)
25′48″ = 25′+48″= 25′+ 0.8′= 25.8′,
计算:
(1) 把25.72°用度、分、秒的形式表示;
(2) 把45°12′30″化成度.
解: (1) ∵0.72°= 0.72× 60′=43.2′,
0.2× 60″=12″,
∴25.72°=25°43′12″
(2) ∵30″= 30× ()′=0.5′,
12.5× ()°≈0. 21°,
∴45°12′30″≈45. 21°
除不尽可以四舍五入取近似值
计算:
(1) 37°28′ + 24°35′; (2) 83°20′- 45°38′20″
解 (1) 37°28′+ 24°35′ = 61°63′ = 62°3′;
(2) 83°20′ - 45°38′20″
= 82°79′60″ - 45°38′20″
= 37°41′40″.
逢“60”进 “1”
不够减,向前一位借“1”
计算:
(1) 20°26′ + 30°54′; (2) 90°- 43°18′.
解 (1) 20°26′+ 35°54′
= 55°80′
= 56°20′;
(2) 90° -43°18′
= 89°60′- 43°18′
= 46°42′.
(1) 把度换算成度、分、秒:从左往右依次进行. 整数度保持不变,把不满 1 度的小数度化为分,再把不满 1 分的小数分化为秒,最后把度、分、秒合写在一起.
(2) 把度、分、秒换算成度:从右往左进行. 先把秒化为分,再把分化为度,最后把原来的度与由分和秒转化成的度相加.
角度单位之间的换算方法:
课堂练习
1. 下列算式正确的是( )
①33.33°=33°3′3″;
②33.33°=33°19′48″;
③50°40′33″=50.43°;
④50°40′30″=50.675°.
A. ①和②
B. ①和③
C. ②和③
D. ②和④
D
【教材P164页 练习第1题】
2. 填空:
(1) 0.65°= ′;
(2) 32.43°= ° ′ ″;
(3) 120°36′54″= °;
(4) 108°42′36″ = °.
39
32
25
48
120.615
108.71
4. 若∠C = 90°,∠A = 25°30′,则 ∠C-∠A 的结果是( )
A. 75°30′ B. 74°30′
C. 65°30′ D. 64°30′
D
3. 比较大小:74.45°_______ 74°45′
<
5. 计算:
(1) 72°12′ + 50°40′30″;
(2) 113°50′40″ - 57°48′42″.
122°52′30″
56°1′58″
【教材P164页 练习第2题】
6. 10 时整,钟表的时针与分针之间所成的角的度数是多少?15 时整呢?
答:10 时整,钟表的时针与分针之间所成的角度数为 60 度,15时整所成的角是 90 度.
【教材P164页 练习第3题】
7. 小红早晨8:30出发,中午12:30到家,则小红出发时时针和分针的夹角为_______,到家时时针和分针的夹角为_______.
75°
165°
解析:与12点整相比,8:30时,
时针转过了 (8+ )×30°=255°,
分针转过了 30×6°=180°,
所以夹角为255°-180°=75°.
同理12:30时,时针和分针的夹角为165°.
1. 若, ,
,则( )
A
A. B.
C. D.
返回
(第2题)
2. [2024广东]如图,一把直尺、
两个含 的三角尺拼接在一起,
则 的度数为( )
C
A. B.
C. D.
返回
3. 将与两个角的关系记为 ,下列探索
的大小与两个角的类型之间的关系中正确的是( )
A
A. 当时,若为锐角,则 为锐角
B. 当时,若为钝角,则 为钝角
C. 当时,若为锐角,则 为锐角
D. 当时,若为锐角,则 为钝角
返回
4. 当分针指向12,时针恰好与分针成
角时是( )
D
A. 9点钟 B. 8点钟
C. 4点钟 D. 8点钟或4点钟
【点拨】当分针指向12,与时
针的夹角为 时,有如图
两种情况,此时是8点钟或4点
钟,故选D.
返回
5. 用一副三角板可以画出一些角.在 , , ,
, , , , , , ,
的角中,能画出的角有( )
A
A. 11个 B. 10个
C. 9个 D. 8个
返回
6.将量角器按如图方式放置,其中角度为 的角是_______
________.
和
(第6题)
返回
7.计算:
(1) ;
【解】 .
(2) ;
.
(3) ;
.
(4) .
.
返回
8. 将一副三角尺按如图方式摆放,使三角尺的一个顶点重
合, , ,和分别是 和
的平分线.若 ,下列结论错误的是( )
D
A.
B.
C.
D.
【点拨】因为 ,
,和 分别是
和 的平分线,所以
,
.因为 ,所以
,
,
, .
返回
9.[2025长沙望城区模拟]如图,是直线上一点, 平
分,平分 .
(1)求出 的度数,你能得出什么结论?
【解】由角平分线的定义可知
, .
再由题图中角的关系得
,
所以 .
结论:的度数恒为 ,和射线 的位置无关.
(2)如果,求 的度数.
由(1)可得 ,所以 .
返回
课堂小结
角的度量与计算
角的分类
角的单位换算
借位
进位
角的和、差计算
大单位化成小单位
小单位化成大单位
谢谢观看!
同课章节目录
