4.3.2.2余角和补角 课件(共36张PPT)
文档属性
| 名称 | 4.3.2.2余角和补角 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 12.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 07:58:50 | ||
图片预览






文档简介
(共36张PPT)
4.3.2.2余角和补角
第4章 图形的认识
【2024新教材】湘教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
余角和补角
在深入学习角的度量与计算后,我们将进一步探索两个重要的角的关系概念 —— 余角和补角。理解余角和补角的定义、性质及其应用,能帮助我们更灵活地解决与角相关的数学问题,同时也为后续学习三角形内角关系、几何图形中的角度计算等知识奠定基础。
一、余角和补角的定义
(一)余角的定义
如果两个角的和等于\(90^{\circ}\)(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角 。例如,\(30^{\circ}\)的角与\(60^{\circ}\)的角,因为\(30^{\circ} + 60^{\circ} = 90^{\circ}\),所以\(30^{\circ}\)角是\(60^{\circ}\)角的余角,同时\(60^{\circ}\)角也是\(30^{\circ}\)角的余角 。一般地,若\(\angle\alpha\)与\(\angle\beta\)互为余角,则可表示为\(\angle\alpha + \angle\beta = 90^{\circ}\),也可以写成\(\angle\beta = 90^{\circ} - \angle\alpha\),\(\angle\alpha = 90^{\circ} - \angle\beta\) 。
(二)补角的定义
如果两个角的和等于\(180^{\circ}\)(平角),就说这两个角互为补角,即其中每一个角是另一个角的补角 。比如,\(100^{\circ}\)的角和\(80^{\circ}\)的角,由于\(100^{\circ} + 80^{\circ} = 180^{\circ}\),所以\(100^{\circ}\)角是\(80^{\circ}\)角的补角,\(80^{\circ}\)角也是\(100^{\circ}\)角的补角 。通常,若\(\angle\theta\)与\(\angle\varphi\)互为补角,可表示为\(\angle\theta + \angle\varphi = 180^{\circ}\),也能写成\(\angle\varphi = 180^{\circ} - \angle\theta\),\(\angle\theta = 180^{\circ} - \angle\varphi\) 。
二、余角和补角的性质
(一)余角的性质
同角的余角相等:若\(\angle A + \angle B = 90^{\circ}\),\(\angle A + \angle C = 90^{\circ}\),那么\(\angle B = \angle C\) 。因为\(\angle B = 90^{\circ} - \angle A\),\(\angle C = 90^{\circ} - \angle A\),所以\(\angle B\)和\(\angle C\)都等于\(90^{\circ}\)减去同一个角\(\angle A\),故\(\angle B = \angle C\) 。
等角的余角相等:若\(\angle A + \angle B = 90^{\circ}\),\(\angle D + \angle C = 90^{\circ}\),且\(\angle A = \angle D\),那么\(\angle B = \angle C\) 。因为\(\angle B = 90^{\circ} - \angle A\),\(\angle C = 90^{\circ} - \angle D\),又因为\(\angle A = \angle D\),所以\(90^{\circ} - \angle A = 90^{\circ} - \angle D\),即\(\angle B = \angle C\) 。
(二)补角的性质
同角的补角相等:若\(\angle M + \angle N = 180^{\circ}\),\(\angle M + \angle P = 180^{\circ}\),则\(\angle N = \angle P\) 。原因是\(\angle N = 180^{\circ} - \angle M\),\(\angle P = 180^{\circ} - \angle M\),所以\(\angle N\)和\(\angle P\)都等于\(180^{\circ}\)减去同一个角\(\angle M\),因此\(\angle N = \angle P\) 。
等角的补角相等:若\(\angle Q + \angle R = 180^{\circ}\),\(\angle S + \angle T = 180^{\circ}\),且\(\angle Q = \angle S\),那么\(\angle R = \angle T\) 。由于\(\angle R = 180^{\circ} - \angle Q\),\(\angle T = 180^{\circ} - \angle S\),再结合\(\angle Q = \angle S\),可得\(180^{\circ} - \angle Q = 180^{\circ} - \angle S\),即\(\angle R = \angle T\) 。
三、余角和补角的应用
(一)在几何图形中的应用
在几何图形中,余角和补角的概念经常用于计算角的度数。例如,在直角三角形中,除直角外的两个锐角互为余角 。已知一个锐角为\(35^{\circ}\),根据余角的定义,另一个锐角的度数为\(90^{\circ} - 35^{\circ} = 55^{\circ}\) 。又如,在一条直线上有三个角\(\angle 1\)、\(\angle 2\)、\(\angle 3\),且\(\angle 1 + \angle 2 + \angle 3 = 180^{\circ}\),如果\(\angle 1\)与\(\angle 2\)互为补角,\(\angle 1 = 120^{\circ}\),那么\(\angle 2 = 180^{\circ} - 120^{\circ} = 60^{\circ}\),进而可求出\(\angle 3 = 180^{\circ} - 120^{\circ} - 60^{\circ} = 0^{\circ}\)(这种情况在实际图形中较少出现,但从数学计算角度成立) 。
(二)在实际生活中的应用
在实际生活中,余角和补角的知识也有广泛应用。比如,在建筑设计中,设计师需要计算不同构件之间的角度,利用余角和补角的关系可以更准确地确定角度,确保建筑物的结构稳定 。在测量工作中,测量人员通过测量一些已知角度,利用余角和补角的性质计算出其他未知角度,从而完成地形测绘等工作 。
四、余角和补角学习中的易错点
概念混淆:容易将余角和补角的定义混淆,错误地认为和为\(180^{\circ}\)的两个角是余角,和为\(90^{\circ}\)的两个角是补角 。可以通过制作口诀 “余角九十要记牢,补角一百八十跑” 来加强记忆。
性质应用错误:在使用同角或等角的余角、补角相等的性质时,容易找错对应角。例如,在复杂的几何图形中,没有准确判断出哪些角是同角或等角的余角、补角,从而错误应用性质 。解决这类问题时,需要仔细分析图形,明确角之间的关系。
计算错误:在计算余角或补角的度数时,可能会出现计算失误。比如在计算\(180^{\circ} - 37^{\circ}25'\)时,度、分的换算错误,正确的计算应为\(180^{\circ} = 179^{\circ}60'\),则\(180^{\circ} - 37^{\circ}25' = 179^{\circ}60' - 37^{\circ}25' = 142^{\circ}35'\) 。
通过对余角和补角的学习,我们掌握了它们的定义、性质以及在不同场景下的应用,同时也了解了学习过程中的易错点。在后续的学习中,要多结合实际问题和几何图形进行练习,熟练运用余角和补角的知识解决问题。如果还有疑问,欢迎随时交流探讨,我们一起深入理解这部分重要的几何知识。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
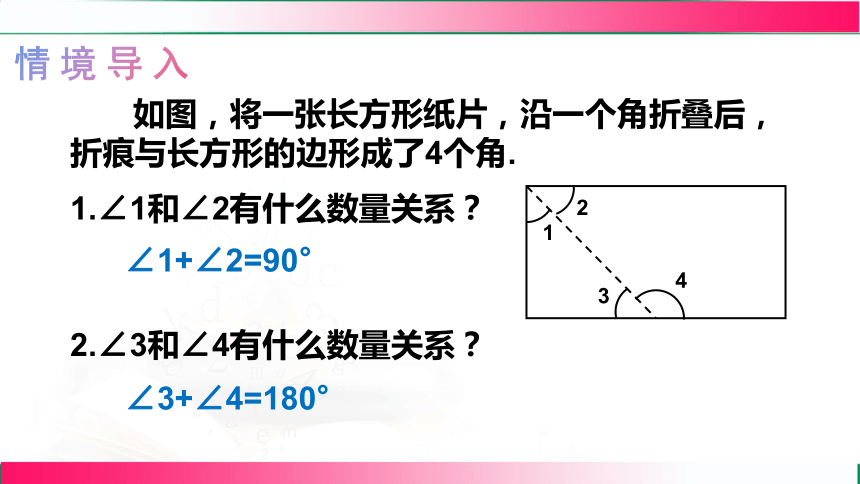
情境导入
如图,将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角.
1
2
3
4
1.∠1和∠2有什么数量关系?
2.∠3和∠4有什么数量关系?
∠1+∠2=90°
∠3+∠4=180°
探索新知
余角和补角的定义
如果两个角的和等于一个直角(90°),那么就说这两个角互为余角(简称互余),也说其中一个角是另一个角的余角.
若∠1+∠2= 90°,则∠1 与∠2 互为余角,其中∠1 是∠2 的余角, ∠2 也是∠1的余角.
1
2
几何语言:
∵∠1+∠2=90°,
∴∠1与∠2互为余角.
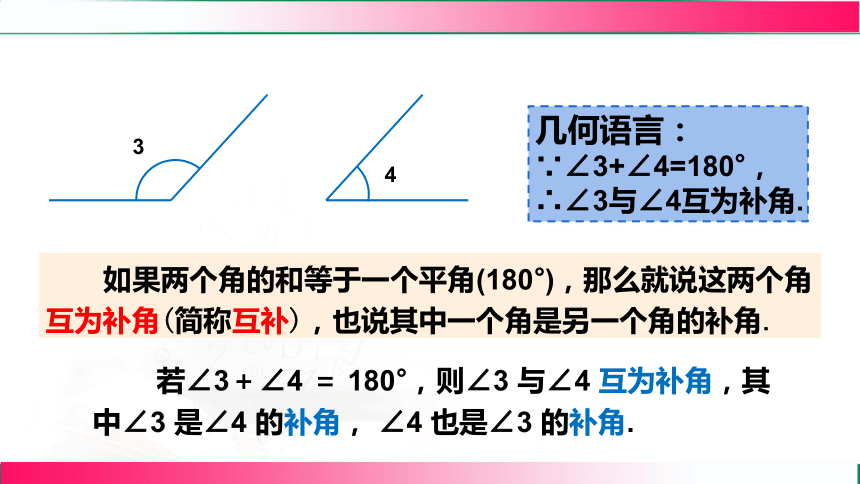
如果两个角的和等于一个平角(180°),那么就说这两个角互为补角(简称互补),也说其中一个角是另一个角的补角.
若∠3+∠4 = 180°,则∠3 与∠4 互为补角,其中∠3 是∠4 的补角, ∠4 也是∠3 的补角.
几何语言:
∵∠3+∠4=180°,
∴∠3与∠4互为补角.
3
4
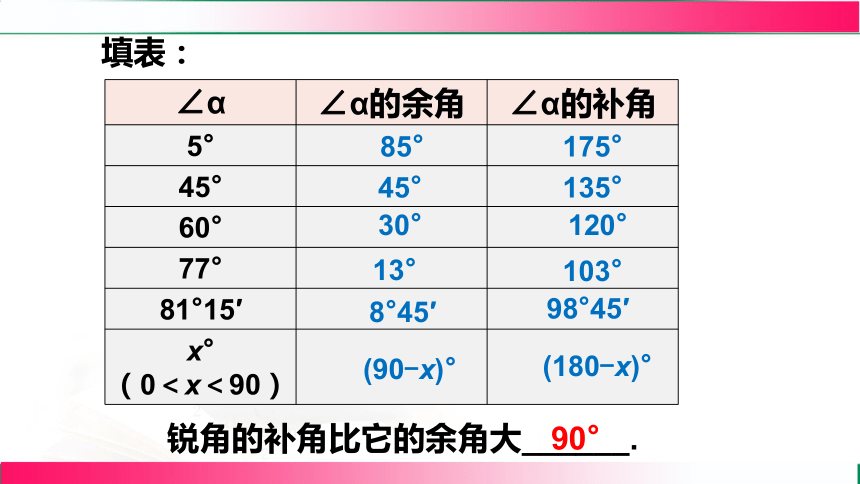
∠α ∠α的余角 ∠α的补角
5°
45°
60°
77°
81°15′
x° (0<x<90)
85°
175°
45°
135°
30°
120°
13°
103°
8°45′
98°45′
(90-x)°
(180-x)°
锐角的补角比它的余角大______.
90°
填表:
判断:
(1) 一个角的余角必为锐角.
(2) 一个角的补角必为钝角.
(3) 同一个锐角的补角比它的余角大90°.
(4) 互余的两个角一定都是锐角,两个锐角一定互余.
(5) 如果∠1=30°,∠2=25°,∠3=35°,那么∠ 1、 ∠ 2、∠3这三个角互为余角.
( )
( )
( )
( )
( )
√
×
√
×
×
练一练
余角和补角的性质
思 考
∠1 ∠2 ∠3
30° 150° 150°
90° 90° 90°
150° 30° 30°
观察下表,你有什么发现?
∠1 与∠2 互补,∠1 与∠3 互补,
∠2与∠3大小相等.
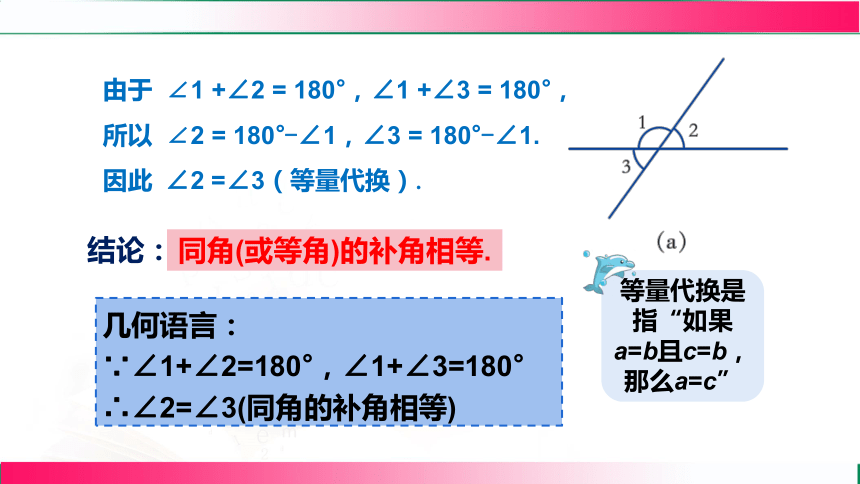
由于 ∠1 +∠2 = 180°,∠1 +∠3 = 180°,
所以 ∠2 = 180°-∠1,∠3 = 180°-∠1.
因此 ∠2 =∠3(等量代换).
结论:
同角(或等角)的补角相等.
几何语言:
∵∠1+∠2=180°,∠1+∠3=180°
∴∠2=∠3(同角的补角相等)
等量代换是指“如果a=b且c=b,那么a=c”
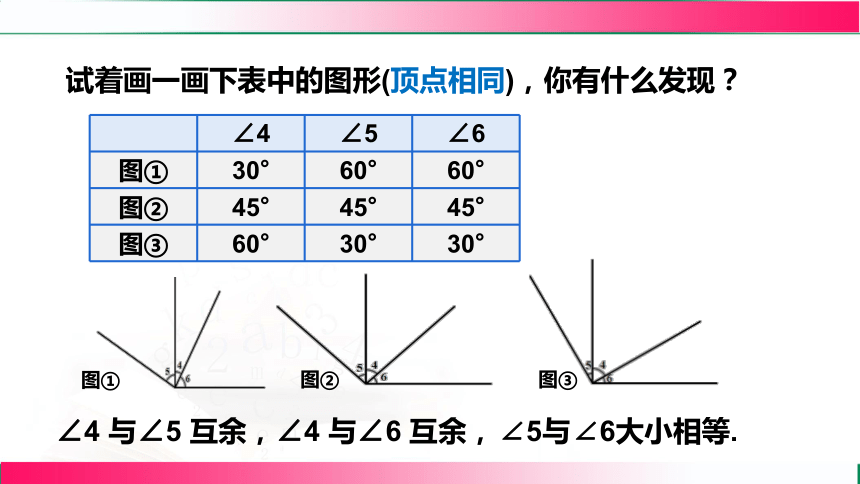
试着画一画下表中的图形(顶点相同),你有什么发现?
∠4 ∠5 ∠6
图① 30° 60° 60°
图② 45° 45° 45°
图③ 60° 30° 30°
∠4 与∠5 互余,∠4 与∠6 互余,
∠5与∠6大小相等.
图①
图②
图③
由于 ∠4 +∠5= 90°,∠4 +∠6 = 90°,
所以 ∠5 = 90°-∠4,∠6 = 90°-∠4.
因此 ∠5 =∠6(等量代换).
结论:
同角(或等角)的余角相等.
几何语言:
∵∠1+∠2=90°,∠1+∠3=90°
∴∠2=∠3(同角的余角相等)
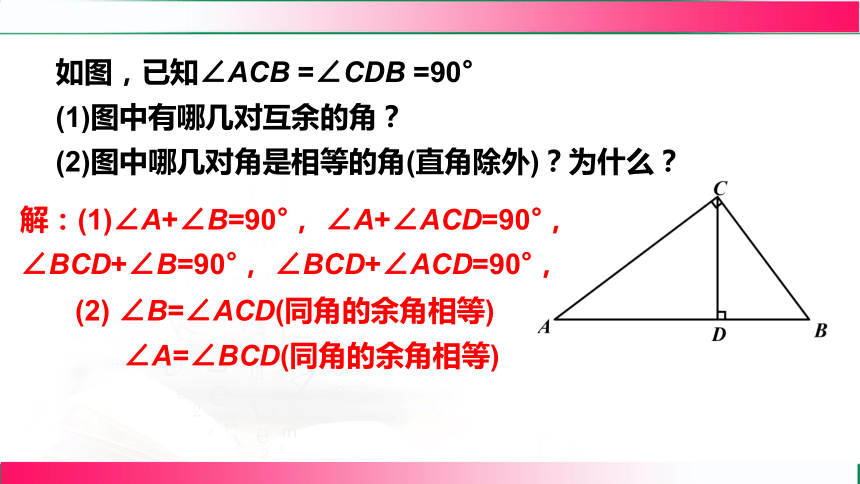
如图,已知∠ACB =∠CDB =90°
(1)图中有哪几对互余的角?
(2)图中哪几对角是相等的角(直角除外)?为什么?
解:(1)∠A+∠B=90°, ∠A+∠ACD=90°,
∠BCD+∠B=90°, ∠BCD+∠ACD=90°,
(2) ∠B=∠ACD(同角的余角相等)
∠A=∠BCD(同角的余角相等)
如图,∠AOB 与∠BOD 互为余角,OC 是
∠BOD 的平分线,∠AOB = 29.66°,求∠COD 的度数.
解 因为∠AOB 与∠BOD 互为余角,
所以∠BOD = 90°-∠AOB
= 90°-29.66°= 60.34°.
又因为 OC 是∠BOD 的平分线,
因此,∠COD 的度数为 30.17°.
所以
已知一个角的余角是这个角的补角的 ,
求这个角的度数.
解 :设这个角为 x°,则这个角的余角为(90-x)°,
补角为(180-x)°.
根据题意,得
解得 x = 45 .
因此,这个角为 45°.
方法总结:涉及到角度的计算时,除常规的和差倍分计算外,通常还需运用方程思想解决问题.
课堂练习
1. 填空:
(1) 105°26′的补角等于 ;
(2) 28°25′32″的余角等于 .
74°34′
61°34′28″
若一个角的补角是这个角的余角的 4 倍,
则这个角的度数为( )
A.30° B.45° C.60° D.65°
C
2.
【课本P166 练习 第1题】
答:∠AOB 的度数为 56°.
如图,∠BOD = 118°,∠COD 是直角, OC 平分∠AOB, 求∠AOB 的度数.
3.
【课本P166 练习 第2题】
4.已知∠A 与∠B 互余,且∠A 的度数比∠B度数的 3 倍还多30°.求∠B的度数.
解 :设∠B的度数为 x°,则∠A的度数为(3x+30)°.
根据题意,得
解得 x = 15 .
故∠B为 15°.
5. 如图,OC 是∠AOD 的平分线,OE 是∠BOD 的平分线. 若∠BOC = 3∠AOD,∠EOD-∠COD = 30°,求 ∠BOE 的度数.
解: 设∠EOD =x°,则∠COD =(x-30)°.
因为 OE 是 ∠BOD 的平分线,
所以 ∠BOE =∠EOD = x°.
因为 OC 是∠AOD 的平分线,
所以∠AOC =∠COD = (x-30)°.
所以∠AOD = 2 (x-30)°,
∠BOC = 2 ∠EOD +∠COD = (2x)°+(x-30)°.
由∠BOC = 3∠AOD,得 2x+x-30= 3×2(x-30),
解得 x = 50. 所以∠BOE = 50°.
1. 若 的余角为,则 的补角的度数是( )
C
A. B.
C. D.
2. [2025长沙望城区期末]一个角的补角比这个角的余角的
3倍少 ,这个角是( )
B
A. B. C. D.
返回
3. [2025汕头月考]如图,, ,
,下列判断:①射线是 的
角平分线;是的补角;;
的余角有和 .其中正确的是( )
C
A. ①③④ B. ①②③
C. ①②③④ D. ②③④
【点拨】因为,所以射线
是 的角平分线,故①正确;因为
,且的补角是 ,所以
是的补角,故②正确;因为 ,
所以 ,所以
.因为 ,所以
,故③正确;因为
,所以
是的余角,是 的余角.因为
,所以的余角有和 ,
故④正确.综上分析可知,正确的有①②③④.
返回
4.如图,将一副三角尺按不同位置摆放.
与 互补的摆法是____;
与 相等的摆法是______.(填序号)
④
①②
返回
5.一位同学利用如图所示的量角器,采用如图①所示的方法
测量锐角 的度数,其中量角器有两条刻度线分别在射
线,上,则 的度数为____.另外一位同学用同样的
方法,测量的余角 的度数,如图②所示,已知射
线所指示的度数为 ,则射线 所指示的度数为_____
_____.
或
返回
6.如图,点在直线 上,
, .
(1)求 的度数.
【解】因为点在直线 上,所以
.
因为 ,
所以 .
又因为 ,
所以 .
所以 .
(2)图中有哪几对角互为余角?
与,与,与, 与
,这4对角互为余角.
(3)图中有哪几对角互为补角?
与,与,与, 与
,与,与,与 ,这7
对角互为补角.
返回
7. 若与互为余角,与 互为补角,则下列结论错误
的是( )
D
A. B.
C. D.
【点拨】因为与互为余角,所以 .因为
与互为补角,所以 ,得
,故A正确,D错误; ,得
,故B正确; ,得
,故C正确.
返回
8.[2025北京海淀区期末]已知 在正方形网格中的位置
如图所示.设的余角为 ,则___ .(填“ ” “
”或“ ”)
【点拨】如图,取格点,,连接 ,
,, ,由网格特征可知:
, ,四
边形 是正方形,所以
,
.因为的余角为 ,所以
.因为 ,
,所以 .
返回
课堂小结
互余 互补
两角间的 数量关系
对应的图形
性质
∠1+∠2=90°
(90°-∠1=∠2)
∠3+∠4=180°
(180°-∠3=∠4)
同角(或等角)的余角相等
同角(或等角)的补角相等
谢谢观看!
4.3.2.2余角和补角
第4章 图形的认识
【2024新教材】湘教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
余角和补角
在深入学习角的度量与计算后,我们将进一步探索两个重要的角的关系概念 —— 余角和补角。理解余角和补角的定义、性质及其应用,能帮助我们更灵活地解决与角相关的数学问题,同时也为后续学习三角形内角关系、几何图形中的角度计算等知识奠定基础。
一、余角和补角的定义
(一)余角的定义
如果两个角的和等于\(90^{\circ}\)(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角 。例如,\(30^{\circ}\)的角与\(60^{\circ}\)的角,因为\(30^{\circ} + 60^{\circ} = 90^{\circ}\),所以\(30^{\circ}\)角是\(60^{\circ}\)角的余角,同时\(60^{\circ}\)角也是\(30^{\circ}\)角的余角 。一般地,若\(\angle\alpha\)与\(\angle\beta\)互为余角,则可表示为\(\angle\alpha + \angle\beta = 90^{\circ}\),也可以写成\(\angle\beta = 90^{\circ} - \angle\alpha\),\(\angle\alpha = 90^{\circ} - \angle\beta\) 。
(二)补角的定义
如果两个角的和等于\(180^{\circ}\)(平角),就说这两个角互为补角,即其中每一个角是另一个角的补角 。比如,\(100^{\circ}\)的角和\(80^{\circ}\)的角,由于\(100^{\circ} + 80^{\circ} = 180^{\circ}\),所以\(100^{\circ}\)角是\(80^{\circ}\)角的补角,\(80^{\circ}\)角也是\(100^{\circ}\)角的补角 。通常,若\(\angle\theta\)与\(\angle\varphi\)互为补角,可表示为\(\angle\theta + \angle\varphi = 180^{\circ}\),也能写成\(\angle\varphi = 180^{\circ} - \angle\theta\),\(\angle\theta = 180^{\circ} - \angle\varphi\) 。
二、余角和补角的性质
(一)余角的性质
同角的余角相等:若\(\angle A + \angle B = 90^{\circ}\),\(\angle A + \angle C = 90^{\circ}\),那么\(\angle B = \angle C\) 。因为\(\angle B = 90^{\circ} - \angle A\),\(\angle C = 90^{\circ} - \angle A\),所以\(\angle B\)和\(\angle C\)都等于\(90^{\circ}\)减去同一个角\(\angle A\),故\(\angle B = \angle C\) 。
等角的余角相等:若\(\angle A + \angle B = 90^{\circ}\),\(\angle D + \angle C = 90^{\circ}\),且\(\angle A = \angle D\),那么\(\angle B = \angle C\) 。因为\(\angle B = 90^{\circ} - \angle A\),\(\angle C = 90^{\circ} - \angle D\),又因为\(\angle A = \angle D\),所以\(90^{\circ} - \angle A = 90^{\circ} - \angle D\),即\(\angle B = \angle C\) 。
(二)补角的性质
同角的补角相等:若\(\angle M + \angle N = 180^{\circ}\),\(\angle M + \angle P = 180^{\circ}\),则\(\angle N = \angle P\) 。原因是\(\angle N = 180^{\circ} - \angle M\),\(\angle P = 180^{\circ} - \angle M\),所以\(\angle N\)和\(\angle P\)都等于\(180^{\circ}\)减去同一个角\(\angle M\),因此\(\angle N = \angle P\) 。
等角的补角相等:若\(\angle Q + \angle R = 180^{\circ}\),\(\angle S + \angle T = 180^{\circ}\),且\(\angle Q = \angle S\),那么\(\angle R = \angle T\) 。由于\(\angle R = 180^{\circ} - \angle Q\),\(\angle T = 180^{\circ} - \angle S\),再结合\(\angle Q = \angle S\),可得\(180^{\circ} - \angle Q = 180^{\circ} - \angle S\),即\(\angle R = \angle T\) 。
三、余角和补角的应用
(一)在几何图形中的应用
在几何图形中,余角和补角的概念经常用于计算角的度数。例如,在直角三角形中,除直角外的两个锐角互为余角 。已知一个锐角为\(35^{\circ}\),根据余角的定义,另一个锐角的度数为\(90^{\circ} - 35^{\circ} = 55^{\circ}\) 。又如,在一条直线上有三个角\(\angle 1\)、\(\angle 2\)、\(\angle 3\),且\(\angle 1 + \angle 2 + \angle 3 = 180^{\circ}\),如果\(\angle 1\)与\(\angle 2\)互为补角,\(\angle 1 = 120^{\circ}\),那么\(\angle 2 = 180^{\circ} - 120^{\circ} = 60^{\circ}\),进而可求出\(\angle 3 = 180^{\circ} - 120^{\circ} - 60^{\circ} = 0^{\circ}\)(这种情况在实际图形中较少出现,但从数学计算角度成立) 。
(二)在实际生活中的应用
在实际生活中,余角和补角的知识也有广泛应用。比如,在建筑设计中,设计师需要计算不同构件之间的角度,利用余角和补角的关系可以更准确地确定角度,确保建筑物的结构稳定 。在测量工作中,测量人员通过测量一些已知角度,利用余角和补角的性质计算出其他未知角度,从而完成地形测绘等工作 。
四、余角和补角学习中的易错点
概念混淆:容易将余角和补角的定义混淆,错误地认为和为\(180^{\circ}\)的两个角是余角,和为\(90^{\circ}\)的两个角是补角 。可以通过制作口诀 “余角九十要记牢,补角一百八十跑” 来加强记忆。
性质应用错误:在使用同角或等角的余角、补角相等的性质时,容易找错对应角。例如,在复杂的几何图形中,没有准确判断出哪些角是同角或等角的余角、补角,从而错误应用性质 。解决这类问题时,需要仔细分析图形,明确角之间的关系。
计算错误:在计算余角或补角的度数时,可能会出现计算失误。比如在计算\(180^{\circ} - 37^{\circ}25'\)时,度、分的换算错误,正确的计算应为\(180^{\circ} = 179^{\circ}60'\),则\(180^{\circ} - 37^{\circ}25' = 179^{\circ}60' - 37^{\circ}25' = 142^{\circ}35'\) 。
通过对余角和补角的学习,我们掌握了它们的定义、性质以及在不同场景下的应用,同时也了解了学习过程中的易错点。在后续的学习中,要多结合实际问题和几何图形进行练习,熟练运用余角和补角的知识解决问题。如果还有疑问,欢迎随时交流探讨,我们一起深入理解这部分重要的几何知识。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
情境导入
如图,将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角.
1
2
3
4
1.∠1和∠2有什么数量关系?
2.∠3和∠4有什么数量关系?
∠1+∠2=90°
∠3+∠4=180°
探索新知
余角和补角的定义
如果两个角的和等于一个直角(90°),那么就说这两个角互为余角(简称互余),也说其中一个角是另一个角的余角.
若∠1+∠2= 90°,则∠1 与∠2 互为余角,其中∠1 是∠2 的余角, ∠2 也是∠1的余角.
1
2
几何语言:
∵∠1+∠2=90°,
∴∠1与∠2互为余角.
如果两个角的和等于一个平角(180°),那么就说这两个角互为补角(简称互补),也说其中一个角是另一个角的补角.
若∠3+∠4 = 180°,则∠3 与∠4 互为补角,其中∠3 是∠4 的补角, ∠4 也是∠3 的补角.
几何语言:
∵∠3+∠4=180°,
∴∠3与∠4互为补角.
3
4
∠α ∠α的余角 ∠α的补角
5°
45°
60°
77°
81°15′
x° (0<x<90)
85°
175°
45°
135°
30°
120°
13°
103°
8°45′
98°45′
(90-x)°
(180-x)°
锐角的补角比它的余角大______.
90°
填表:
判断:
(1) 一个角的余角必为锐角.
(2) 一个角的补角必为钝角.
(3) 同一个锐角的补角比它的余角大90°.
(4) 互余的两个角一定都是锐角,两个锐角一定互余.
(5) 如果∠1=30°,∠2=25°,∠3=35°,那么∠ 1、 ∠ 2、∠3这三个角互为余角.
( )
( )
( )
( )
( )
√
×
√
×
×
练一练
余角和补角的性质
思 考
∠1 ∠2 ∠3
30° 150° 150°
90° 90° 90°
150° 30° 30°
观察下表,你有什么发现?
∠1 与∠2 互补,∠1 与∠3 互补,
∠2与∠3大小相等.
由于 ∠1 +∠2 = 180°,∠1 +∠3 = 180°,
所以 ∠2 = 180°-∠1,∠3 = 180°-∠1.
因此 ∠2 =∠3(等量代换).
结论:
同角(或等角)的补角相等.
几何语言:
∵∠1+∠2=180°,∠1+∠3=180°
∴∠2=∠3(同角的补角相等)
等量代换是指“如果a=b且c=b,那么a=c”
试着画一画下表中的图形(顶点相同),你有什么发现?
∠4 ∠5 ∠6
图① 30° 60° 60°
图② 45° 45° 45°
图③ 60° 30° 30°
∠4 与∠5 互余,∠4 与∠6 互余,
∠5与∠6大小相等.
图①
图②
图③
由于 ∠4 +∠5= 90°,∠4 +∠6 = 90°,
所以 ∠5 = 90°-∠4,∠6 = 90°-∠4.
因此 ∠5 =∠6(等量代换).
结论:
同角(或等角)的余角相等.
几何语言:
∵∠1+∠2=90°,∠1+∠3=90°
∴∠2=∠3(同角的余角相等)
如图,已知∠ACB =∠CDB =90°
(1)图中有哪几对互余的角?
(2)图中哪几对角是相等的角(直角除外)?为什么?
解:(1)∠A+∠B=90°, ∠A+∠ACD=90°,
∠BCD+∠B=90°, ∠BCD+∠ACD=90°,
(2) ∠B=∠ACD(同角的余角相等)
∠A=∠BCD(同角的余角相等)
如图,∠AOB 与∠BOD 互为余角,OC 是
∠BOD 的平分线,∠AOB = 29.66°,求∠COD 的度数.
解 因为∠AOB 与∠BOD 互为余角,
所以∠BOD = 90°-∠AOB
= 90°-29.66°= 60.34°.
又因为 OC 是∠BOD 的平分线,
因此,∠COD 的度数为 30.17°.
所以
已知一个角的余角是这个角的补角的 ,
求这个角的度数.
解 :设这个角为 x°,则这个角的余角为(90-x)°,
补角为(180-x)°.
根据题意,得
解得 x = 45 .
因此,这个角为 45°.
方法总结:涉及到角度的计算时,除常规的和差倍分计算外,通常还需运用方程思想解决问题.
课堂练习
1. 填空:
(1) 105°26′的补角等于 ;
(2) 28°25′32″的余角等于 .
74°34′
61°34′28″
若一个角的补角是这个角的余角的 4 倍,
则这个角的度数为( )
A.30° B.45° C.60° D.65°
C
2.
【课本P166 练习 第1题】
答:∠AOB 的度数为 56°.
如图,∠BOD = 118°,∠COD 是直角, OC 平分∠AOB, 求∠AOB 的度数.
3.
【课本P166 练习 第2题】
4.已知∠A 与∠B 互余,且∠A 的度数比∠B度数的 3 倍还多30°.求∠B的度数.
解 :设∠B的度数为 x°,则∠A的度数为(3x+30)°.
根据题意,得
解得 x = 15 .
故∠B为 15°.
5. 如图,OC 是∠AOD 的平分线,OE 是∠BOD 的平分线. 若∠BOC = 3∠AOD,∠EOD-∠COD = 30°,求 ∠BOE 的度数.
解: 设∠EOD =x°,则∠COD =(x-30)°.
因为 OE 是 ∠BOD 的平分线,
所以 ∠BOE =∠EOD = x°.
因为 OC 是∠AOD 的平分线,
所以∠AOC =∠COD = (x-30)°.
所以∠AOD = 2 (x-30)°,
∠BOC = 2 ∠EOD +∠COD = (2x)°+(x-30)°.
由∠BOC = 3∠AOD,得 2x+x-30= 3×2(x-30),
解得 x = 50. 所以∠BOE = 50°.
1. 若 的余角为,则 的补角的度数是( )
C
A. B.
C. D.
2. [2025长沙望城区期末]一个角的补角比这个角的余角的
3倍少 ,这个角是( )
B
A. B. C. D.
返回
3. [2025汕头月考]如图,, ,
,下列判断:①射线是 的
角平分线;是的补角;;
的余角有和 .其中正确的是( )
C
A. ①③④ B. ①②③
C. ①②③④ D. ②③④
【点拨】因为,所以射线
是 的角平分线,故①正确;因为
,且的补角是 ,所以
是的补角,故②正确;因为 ,
所以 ,所以
.因为 ,所以
,故③正确;因为
,所以
是的余角,是 的余角.因为
,所以的余角有和 ,
故④正确.综上分析可知,正确的有①②③④.
返回
4.如图,将一副三角尺按不同位置摆放.
与 互补的摆法是____;
与 相等的摆法是______.(填序号)
④
①②
返回
5.一位同学利用如图所示的量角器,采用如图①所示的方法
测量锐角 的度数,其中量角器有两条刻度线分别在射
线,上,则 的度数为____.另外一位同学用同样的
方法,测量的余角 的度数,如图②所示,已知射
线所指示的度数为 ,则射线 所指示的度数为_____
_____.
或
返回
6.如图,点在直线 上,
, .
(1)求 的度数.
【解】因为点在直线 上,所以
.
因为 ,
所以 .
又因为 ,
所以 .
所以 .
(2)图中有哪几对角互为余角?
与,与,与, 与
,这4对角互为余角.
(3)图中有哪几对角互为补角?
与,与,与, 与
,与,与,与 ,这7
对角互为补角.
返回
7. 若与互为余角,与 互为补角,则下列结论错误
的是( )
D
A. B.
C. D.
【点拨】因为与互为余角,所以 .因为
与互为补角,所以 ,得
,故A正确,D错误; ,得
,故B正确; ,得
,故C正确.
返回
8.[2025北京海淀区期末]已知 在正方形网格中的位置
如图所示.设的余角为 ,则___ .(填“ ” “
”或“ ”)
【点拨】如图,取格点,,连接 ,
,, ,由网格特征可知:
, ,四
边形 是正方形,所以
,
.因为的余角为 ,所以
.因为 ,
,所以 .
返回
课堂小结
互余 互补
两角间的 数量关系
对应的图形
性质
∠1+∠2=90°
(90°-∠1=∠2)
∠3+∠4=180°
(180°-∠3=∠4)
同角(或等角)的余角相等
同角(或等角)的补角相等
谢谢观看!
同课章节目录
