第2章 代数式【章末复习】 课件(共45张PPT)
文档属性
| 名称 | 第2章 代数式【章末复习】 课件(共45张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 00:00:00 | ||
图片预览











文档简介
(共45张PPT)
章末复习
第2章 代数式
【2024新教材】湘教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第 2 章 代数式章末复习
一、知识框架梳理
(一)代数式的概念
定义:用运算符号(加、减、乘、除、乘方等)把数或表示数的字母连接而成的式子叫做代数式。单独的一个数或者一个字母也叫做代数式 。例如\(5\)、\(a\)、\(3x + 2y\)、\(\frac{m}{n}\)(\(n\neq0\))等都是代数式。需注意,等式(如\(x + 1 = 3\))和不等式(如\(2x > 5\))不属于代数式。
分类:代数式可分为整式和分式。整式包括单项式和多项式;分式是指分母中含有字母的式子,如\(\frac{1}{x}\) 。
(二)整式相关知识
单项式
概念:由数与字母的积组成的代数式叫做单项式,单独的一个数或一个字母也叫做单项式 。例如\( - 2xy\)、\(7\)、\(a\)等。
系数和次数:单项式中的数字因数叫做系数;一个单项式中,所有字母的指数的和叫做次数 。如\( - 3x^2y\)的系数是\( - 3\),次数是\(2 + 1 = 3\) 。
多项式
概念:几个单项式的和叫做多项式 。例如\(x^2 - 3x + 2\)。
项和次数:在多项式中,每个单项式叫做多项式的项,不含字母的项叫做常数项;多项式里,次数最高项的次数,就是这个多项式的次数 。对于\(2x^3 - x^2 + 5x - 1\),有四项,常数项是\( - 1\),次数是\(3\) 。
整式的加减
运算基础:依据同类项的概念和去括号法则。同类项是指所含字母相同,并且相同字母的指数也相同的项 ;去括号法则为:括号前是 “\(+\)”,去括号后各项符号不变;括号前是 “\(-\)”,去括号后各项符号改变;括号前是数字因数,利用乘法分配律去括号 。
运算步骤:先去括号,再合并同类项 。例如计算\((2x^2 - 3x + 1) - (x^2 + 2x - 3)=2x^2 - 3x + 1 - x^2 - 2x + 3=x^2 - 5x + 4\) 。
(三)代数式的值
用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果,叫做代数式的值 。例如,对于代数式\(2x - 1\),当\(x = 3\)时,代入计算\(2 3 - 1 = 5\),\(5\)就是该代数式在\(x = 3\)时的值 。
(四)列代数式
根据实际问题中的数量关系,用数、字母和运算符号列出代数式 。例如,某商品原价为\(a\)元,打八折后的价格可列代数式为\(0.8a\)元 ;一个长方形的长为\(x\),宽比长少\(2\),其面积可表示为\(x(x - 2)\) 。
二、典型例题讲解
(一)代数式概念辨析
例 1:下列式子中,属于代数式的是( )
A. \(x = 1\) B. \(2x - 1 > 0\) C. \(a^2 + b\) D. \(a + b = c\)
解析:A 选项\(x = 1\)是等式,B 选项\(2x - 1 > 0\)是不等式,D 选项\(a + b = c\)是等式,均不属于代数式;C 选项\(a^2 + b\)是用运算符号把数和字母连接而成的式子,属于代数式。答案选 C。
(二)整式相关计算
例 2:指出单项式\(-\frac{2}{3}xy^2\)的系数和次数。
解析:根据单项式系数和次数的定义,该单项式的系数是\(-\frac{2}{3}\),\(x\)的指数是\(1\),\(y\)的指数是\(2\),次数为\(1 + 2 = 3\) 。
例 3:计算\((3x^2 - 2x + 1) - (2x^2 + 3x - 5)\)
解析:
去括号:根据去括号法则,原式变为\(3x^2 - 2x + 1 - 2x^2 - 3x + 5\) 。
合并同类项:\((3x^2 - 2x^2)+(-2x - 3x)+(1 + 5)=x^2 - 5x + 6\) 。
(三)求代数式的值
例 4:已知\(x = - 2\),求代数式\(3x^2 - 2x + 1\)的值。
解析:将\(x = - 2\)代入代数式,\(3 (-2)^2 - 2 (-2) + 1 = 3 4 + 4 + 1 = 12 + 4 + 1 = 17\) 。
(四)列代数式应用
例 5:某工厂原计划每月生产\(a\)个零件,实际每月增产\(20\%\),则实际每月生产多少个零件?
解析:实际每月生产的零件数是在原计划生产数量的基础上增加\(20\%\),即\(a + 20\%a = 1.2a\)个 。
三、巩固练习
(一)选择题
下列式子中不是代数式的是( )
A. \(\frac{1}{x}\) B. \(0\) C. \(x = 1\) D. \(2x + 3y\)
单项式\(-5x^2y\)的系数和次数分别是( )
A. \(-5\),\(2\) B. \(-5\),\(3\) C. \(5\),\(2\) D. \(5\),\(3\)
化简\((2x - 3y) - (5x - 4y)\)的结果是( )
A. \(-3x - y\) B. \(-3x + y\) C. \(3x - y\) D. \(3x + y\)
(二)填空题
多项式\(3x^2 - 2x + 1\)的次数是______,常数项是______。
当\(x = 3\)时,代数式\(2x^2 - 4x + 5\)的值为______。
某本书的单价是\(a\)元,购买\(n\)本需要______元。
(三)解答题
化简:\(3(2a^2 - b^2) - 2(3a^2 + 2b^2)\)
已知\(a = - 1\),\(b = 2\),求代数式\(a^2b - 2ab + 3\)的值 。
一个梯形的上底为\(a\),下底比上底长\(b\),高为\(h\),用代数式表示该梯形的面积,并求当\(a = 3\),\(b = 2\),\(h = 4\)时梯形的面积 。
通过对本章知识的系统复习,希望同学们能够查漏补缺,熟练掌握代数式相关的概念、运算及应用。在练习过程中,认真分析错题,总结解题方法和技巧,进一步提升数学学习能力。若还有疑问,随时交流探讨。
这份复习资料全面覆盖代数式章节要点。你可以说说对内容深度、例题难度等方面的看法,若想增减某些知识点,也能随时沟通调整。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
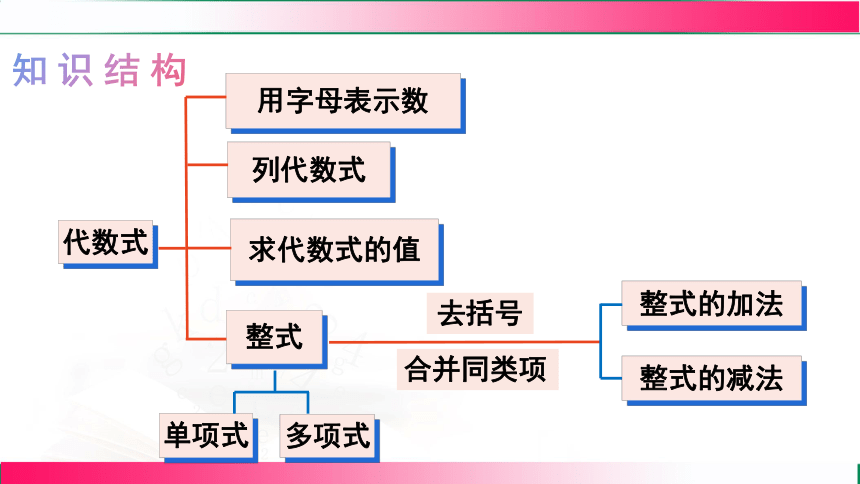
知识结构
用字母表示数
列代数式
整式
整式的加法
代数式
求代数式的值
单项式
多项式
合并同类项
去括号
整式的减法
思考回顾
1.什么叫作代数式?列代数式时,一般怎样规范书写?
数与表示数的字母用运算符号连接而成的式子叫作代数式.
单独一个字母或一个数也是代数式.
列代数式注意事项
数与字母相乘,乘号通常省略,数字写在字母前面
字母与字母相乘,乘号通常省略不写或写成“·”
相同字母相乘时,应写成乘方的形式.
后面带单位的相加或相减的式子要用括号括起来
式子中出现除法运算时,一般按分数形式来写
做一做
1用代数式填空:
(1) 正方形的边长为a,那么它的周长是_______,面积是
_______;
(2)某地区去年的人均收入为b万元,今后一段时期每年
将以9%的增长率增加,则经过三年增长,该地区人
均收入为___________万元.
4a
a2
(1+9%)3b
2.列代数式:
(1) x 的立方减去 y 的4倍;
(2) a 的相反数与 b(b不为0)的倒数的和;
(3) a 减去 b 的差的平方,再加上a与b的和的平方.
x2-4y
-a +
(a-b)2+(a+b)2
2. 举例说明如何求代数式的值?
将b用一个数代入
得出一个结果
代数式
372.6+4.07b
代入数值时,应该把省略的乘号还原.
代入负数时,根据实际情况添上括号.
乘方运算代入分数时,也必须添上括号.
计算时必须按照代数式指定的运算顺序进行计算.
注意事项:
做一做
1.已知代数式,当x=5,y=3时,求这个代数式的值.
解:当x=5,y=3时,
= = .
3.什么叫作单项式、多项式?单独一个数或字母是单项式吗?单项式的次数、多项式的次数分别是如何确定的?
(1)单项式:
①定义:____________________________的代数式叫做单项式.
②系数:单项式中的_______叫做这个单项式的系数.
③次数:单项式中,所有字母的指数______叫做这个
单项式的次数.
④单独的一个数或字母是单项式.
的和
数字
由数与字母及其幂的乘积组成
(2)多项式:
①定义:几个单项式的__________叫做多项式.
②多项式的项:多项式里,每个__________叫做多项式
的项(包含前面符号).
常数项:不含______的项叫做常数项(包含前面符号);
③多项式的次数:多项式中,次数最高的项的________,
叫作这个多项式的次数.
和
单项式
字母
次数
做一做
(1) 单项式23x2y的系数是 _____,次数是_____.
(2) 多项式x3y2-2x2y+5xy2-6的次数是_____,
项有____________________,常数项是______,
是____次____项式,并按字母____的____幂排序.
8
3
5
x3y2,
-2x2y,
5xy2,
-6
-6
五
四
降
x
4.什么叫作同类项?怎样合并同类项?
把所含字母相同并且相同字母的指数也相同的单项式称为同类项.
一般地,在多项式中,要把同类项的系数相加合并成一项,这叫作合并同类项.
同类项的特征:
两相同
所含______相同.
相同字母的______分别相同.
两无关
两者缺一不可
与__________无关.
与__________无关.
字母
系数大小
字母顺序
所有的常数项都是同类项
指数
“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用
不同的标记标出;
二移,利用加法的交换律,将不同类的同类项集
中到一起;
三合,将同一括号内的同类项相加即可.
系数相加,字母和字母的指数不变.
做一做
1、下列各组是不是同类项:
(1)4abc 与 4ab
(2)–5 m2 n3 与 2n3 m2
(3)–0.3 x2 y 与 y x2
不是
是
是
2、合并下列同类项:
(1)3xy – 4 xy – xy = ( )
(2)– a – a – 2a=( )
(3)0.8ab3 – a3 b+0.2ab3 =( )
–2xy
–4a
ab3–a3b
5.举例说明如何进行整式的加减运算.
去括号法则:
括号前是“+”,可以直接去掉括号,原括号里各项符号都不变;
括号前是“- ”,去掉括号和它前面的“-”时,原括号里各项符号均要改变.
考点1 代数式
1. [2025长沙望城区期末]下列各式:; ;
;;; 中,是代数式的有
( )
B
A. 3个 B. 4个 C. 5个 D. 6个
【点拨】由代数式的定义可知,是代数式的有 ;
;; ,共4个.
返回
考点2 列代数式
2.如图,有一块长为18米,宽为10米的
长方形土地,现将三面留出宽都是
米的小路,余下的部分是
菜地,用含 的式子表示:
(1)菜地的长为__________米,宽为_________米;
(2)菜地的面积为_________________平方米.
返回
考点3 求代数式的值
3. 如果代数式 的值是7,那么代数
式 的值等于( )
D
A. 2 B. 3 C. D. 15
【点拨】因为 ,所以
.
返回
考点4 整式的相关概念
4.下列各式:,,,,,
,, 中,是整式的有______________,
是单项式的有________,是多项式的有________.(填序号)
①②③④⑥⑦
①②⑥
③④⑦
5.已知,均为有理数,
是关于的二次三项式,则 ___.
0
返回
6.若关于,的单项式与 的系数、次数均相同,
求, 的值.
【解】因为关于,的单项式与 的系数、次数
均相同,
所以,,解得, .
返回
考点5 同类项及合并同类项
7. [2025深圳月考]若单项式与 是同类项,
则 的值是( )
A
A. B. 0 C. 1 D. 2 025
【点拨】由题意,得,,所以 ,所以
.
返回
8. 下列化简正确的是( )
D
A. B.
C. D.
返回
考点6 整式的加减
9.[2025北京师大附中月考]先化简,再求值:
,其中, .
【解】
.
当, 时,原式
.
返回
10. 已知 ,小明同
学错将“”看成“ ”,算得的结果为
.
(1)求 ;
【解】因为 ,
,
所以
.
(2)求 .
.
返回
考点7 整式加减的应用
11. 一粥一饭,当思来之不易;半丝半缕,恒念
物力维艰.为了让同学们养成良好的节约习惯,学生会倡导的
勤工俭学活动效果显著,每个班级把本班的废弃试卷、书本
进行分类整理,每周把废品统一卖出,钱款用于班级日常开
支,上周七年级一班收入 元,二班收入比一班收入的2倍少
80元,三班收入比二班收入的一半多100元.
(1)用含 的式子表示三个班的上周总收入;
【解】三个班的上周总收入是
(元).
(2)当 时,求三个班的上周总收入.
当 时,
三个班的上周总收入是 (元).
返回
12.如图是2025年12月的日历.
(1)带阴影的十字框中的5个数之和
与十字框中心的数有什么关系?
【解】带阴影的十字框中的5个数之和
是十字框中心的数的5倍.
(2)不改变十字框的大小,如果将带阴影的十字框移至其
他几个位置,你能得出什么结论?你知道为什么吗?
带阴影的十字框中的5个数之和是十字
框中心的数的5倍,理由如下:设十字
框中心的数为 ,则其余4个数分别为
,,, ,所以带阴影的
十字框中的5个数之和为
所以带阴影的十字框中的5个数之和是十字框中心的数的5倍.
,
(3)这个结论对于任何一个月的日历都成立吗?
这个结论对于任何一个月的日历都成立.
返回
考点8 规律探究
13. 莫高窟坐落于河西
走廊西部的尽头——敦煌,是我国古
29
代文明的璀璨艺术宝库.莫高窟保存壁画4.5万多平方米,具
有独特的形式美感和艺术魅力.小明发现,壁画纹样中还蕴藏
着数学知识,如图,第①个图案中有5个花朵图案,第②个图
案中有8个花朵图案,第③个图案中有11个花朵图案, ,
按此规律排列下去,则第⑨个图案中花朵图案的个数为____.
【点拨】由题知,第①个图案
中有 (个)花朵
图案,第②个图案中有 (个)花朵图案,第③
个图案中有(个)花朵图案, ,依此规律,
第 个图案中有 (个)花朵图案,
所以第⑨个图案中花朵图案的个数为 .
返回
思想1 分类讨论思想
14.已知与的和是单项式,是常数,求,
的值或取值范围.
【解】由题意分以下两种情况讨论:
(1)当时, 可取任意数;
(2)当 时,由已知可得两个单项式为同类项,则
,解得 .
综上所述,,取任意数或, .
返回
思想2 整体思想
15. 已知, ,则
的值是( )
D
A. 18 B. 19 C. 20 D. 21
返回
思想3 数形结合思想
16. 有理数,,, 在数轴上对应点的位置如图所示,
若 ,则
的值是( )
B
A. 77 B. 78 C. D.
【点拨】由数轴可得 ,
所以,, .
所以
.
所以 .
所以
.
返回
谢谢观看!
章末复习
第2章 代数式
【2024新教材】湘教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第 2 章 代数式章末复习
一、知识框架梳理
(一)代数式的概念
定义:用运算符号(加、减、乘、除、乘方等)把数或表示数的字母连接而成的式子叫做代数式。单独的一个数或者一个字母也叫做代数式 。例如\(5\)、\(a\)、\(3x + 2y\)、\(\frac{m}{n}\)(\(n\neq0\))等都是代数式。需注意,等式(如\(x + 1 = 3\))和不等式(如\(2x > 5\))不属于代数式。
分类:代数式可分为整式和分式。整式包括单项式和多项式;分式是指分母中含有字母的式子,如\(\frac{1}{x}\) 。
(二)整式相关知识
单项式
概念:由数与字母的积组成的代数式叫做单项式,单独的一个数或一个字母也叫做单项式 。例如\( - 2xy\)、\(7\)、\(a\)等。
系数和次数:单项式中的数字因数叫做系数;一个单项式中,所有字母的指数的和叫做次数 。如\( - 3x^2y\)的系数是\( - 3\),次数是\(2 + 1 = 3\) 。
多项式
概念:几个单项式的和叫做多项式 。例如\(x^2 - 3x + 2\)。
项和次数:在多项式中,每个单项式叫做多项式的项,不含字母的项叫做常数项;多项式里,次数最高项的次数,就是这个多项式的次数 。对于\(2x^3 - x^2 + 5x - 1\),有四项,常数项是\( - 1\),次数是\(3\) 。
整式的加减
运算基础:依据同类项的概念和去括号法则。同类项是指所含字母相同,并且相同字母的指数也相同的项 ;去括号法则为:括号前是 “\(+\)”,去括号后各项符号不变;括号前是 “\(-\)”,去括号后各项符号改变;括号前是数字因数,利用乘法分配律去括号 。
运算步骤:先去括号,再合并同类项 。例如计算\((2x^2 - 3x + 1) - (x^2 + 2x - 3)=2x^2 - 3x + 1 - x^2 - 2x + 3=x^2 - 5x + 4\) 。
(三)代数式的值
用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果,叫做代数式的值 。例如,对于代数式\(2x - 1\),当\(x = 3\)时,代入计算\(2 3 - 1 = 5\),\(5\)就是该代数式在\(x = 3\)时的值 。
(四)列代数式
根据实际问题中的数量关系,用数、字母和运算符号列出代数式 。例如,某商品原价为\(a\)元,打八折后的价格可列代数式为\(0.8a\)元 ;一个长方形的长为\(x\),宽比长少\(2\),其面积可表示为\(x(x - 2)\) 。
二、典型例题讲解
(一)代数式概念辨析
例 1:下列式子中,属于代数式的是( )
A. \(x = 1\) B. \(2x - 1 > 0\) C. \(a^2 + b\) D. \(a + b = c\)
解析:A 选项\(x = 1\)是等式,B 选项\(2x - 1 > 0\)是不等式,D 选项\(a + b = c\)是等式,均不属于代数式;C 选项\(a^2 + b\)是用运算符号把数和字母连接而成的式子,属于代数式。答案选 C。
(二)整式相关计算
例 2:指出单项式\(-\frac{2}{3}xy^2\)的系数和次数。
解析:根据单项式系数和次数的定义,该单项式的系数是\(-\frac{2}{3}\),\(x\)的指数是\(1\),\(y\)的指数是\(2\),次数为\(1 + 2 = 3\) 。
例 3:计算\((3x^2 - 2x + 1) - (2x^2 + 3x - 5)\)
解析:
去括号:根据去括号法则,原式变为\(3x^2 - 2x + 1 - 2x^2 - 3x + 5\) 。
合并同类项:\((3x^2 - 2x^2)+(-2x - 3x)+(1 + 5)=x^2 - 5x + 6\) 。
(三)求代数式的值
例 4:已知\(x = - 2\),求代数式\(3x^2 - 2x + 1\)的值。
解析:将\(x = - 2\)代入代数式,\(3 (-2)^2 - 2 (-2) + 1 = 3 4 + 4 + 1 = 12 + 4 + 1 = 17\) 。
(四)列代数式应用
例 5:某工厂原计划每月生产\(a\)个零件,实际每月增产\(20\%\),则实际每月生产多少个零件?
解析:实际每月生产的零件数是在原计划生产数量的基础上增加\(20\%\),即\(a + 20\%a = 1.2a\)个 。
三、巩固练习
(一)选择题
下列式子中不是代数式的是( )
A. \(\frac{1}{x}\) B. \(0\) C. \(x = 1\) D. \(2x + 3y\)
单项式\(-5x^2y\)的系数和次数分别是( )
A. \(-5\),\(2\) B. \(-5\),\(3\) C. \(5\),\(2\) D. \(5\),\(3\)
化简\((2x - 3y) - (5x - 4y)\)的结果是( )
A. \(-3x - y\) B. \(-3x + y\) C. \(3x - y\) D. \(3x + y\)
(二)填空题
多项式\(3x^2 - 2x + 1\)的次数是______,常数项是______。
当\(x = 3\)时,代数式\(2x^2 - 4x + 5\)的值为______。
某本书的单价是\(a\)元,购买\(n\)本需要______元。
(三)解答题
化简:\(3(2a^2 - b^2) - 2(3a^2 + 2b^2)\)
已知\(a = - 1\),\(b = 2\),求代数式\(a^2b - 2ab + 3\)的值 。
一个梯形的上底为\(a\),下底比上底长\(b\),高为\(h\),用代数式表示该梯形的面积,并求当\(a = 3\),\(b = 2\),\(h = 4\)时梯形的面积 。
通过对本章知识的系统复习,希望同学们能够查漏补缺,熟练掌握代数式相关的概念、运算及应用。在练习过程中,认真分析错题,总结解题方法和技巧,进一步提升数学学习能力。若还有疑问,随时交流探讨。
这份复习资料全面覆盖代数式章节要点。你可以说说对内容深度、例题难度等方面的看法,若想增减某些知识点,也能随时沟通调整。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识结构
用字母表示数
列代数式
整式
整式的加法
代数式
求代数式的值
单项式
多项式
合并同类项
去括号
整式的减法
思考回顾
1.什么叫作代数式?列代数式时,一般怎样规范书写?
数与表示数的字母用运算符号连接而成的式子叫作代数式.
单独一个字母或一个数也是代数式.
列代数式注意事项
数与字母相乘,乘号通常省略,数字写在字母前面
字母与字母相乘,乘号通常省略不写或写成“·”
相同字母相乘时,应写成乘方的形式.
后面带单位的相加或相减的式子要用括号括起来
式子中出现除法运算时,一般按分数形式来写
做一做
1用代数式填空:
(1) 正方形的边长为a,那么它的周长是_______,面积是
_______;
(2)某地区去年的人均收入为b万元,今后一段时期每年
将以9%的增长率增加,则经过三年增长,该地区人
均收入为___________万元.
4a
a2
(1+9%)3b
2.列代数式:
(1) x 的立方减去 y 的4倍;
(2) a 的相反数与 b(b不为0)的倒数的和;
(3) a 减去 b 的差的平方,再加上a与b的和的平方.
x2-4y
-a +
(a-b)2+(a+b)2
2. 举例说明如何求代数式的值?
将b用一个数代入
得出一个结果
代数式
372.6+4.07b
代入数值时,应该把省略的乘号还原.
代入负数时,根据实际情况添上括号.
乘方运算代入分数时,也必须添上括号.
计算时必须按照代数式指定的运算顺序进行计算.
注意事项:
做一做
1.已知代数式,当x=5,y=3时,求这个代数式的值.
解:当x=5,y=3时,
= = .
3.什么叫作单项式、多项式?单独一个数或字母是单项式吗?单项式的次数、多项式的次数分别是如何确定的?
(1)单项式:
①定义:____________________________的代数式叫做单项式.
②系数:单项式中的_______叫做这个单项式的系数.
③次数:单项式中,所有字母的指数______叫做这个
单项式的次数.
④单独的一个数或字母是单项式.
的和
数字
由数与字母及其幂的乘积组成
(2)多项式:
①定义:几个单项式的__________叫做多项式.
②多项式的项:多项式里,每个__________叫做多项式
的项(包含前面符号).
常数项:不含______的项叫做常数项(包含前面符号);
③多项式的次数:多项式中,次数最高的项的________,
叫作这个多项式的次数.
和
单项式
字母
次数
做一做
(1) 单项式23x2y的系数是 _____,次数是_____.
(2) 多项式x3y2-2x2y+5xy2-6的次数是_____,
项有____________________,常数项是______,
是____次____项式,并按字母____的____幂排序.
8
3
5
x3y2,
-2x2y,
5xy2,
-6
-6
五
四
降
x
4.什么叫作同类项?怎样合并同类项?
把所含字母相同并且相同字母的指数也相同的单项式称为同类项.
一般地,在多项式中,要把同类项的系数相加合并成一项,这叫作合并同类项.
同类项的特征:
两相同
所含______相同.
相同字母的______分别相同.
两无关
两者缺一不可
与__________无关.
与__________无关.
字母
系数大小
字母顺序
所有的常数项都是同类项
指数
“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用
不同的标记标出;
二移,利用加法的交换律,将不同类的同类项集
中到一起;
三合,将同一括号内的同类项相加即可.
系数相加,字母和字母的指数不变.
做一做
1、下列各组是不是同类项:
(1)4abc 与 4ab
(2)–5 m2 n3 与 2n3 m2
(3)–0.3 x2 y 与 y x2
不是
是
是
2、合并下列同类项:
(1)3xy – 4 xy – xy = ( )
(2)– a – a – 2a=( )
(3)0.8ab3 – a3 b+0.2ab3 =( )
–2xy
–4a
ab3–a3b
5.举例说明如何进行整式的加减运算.
去括号法则:
括号前是“+”,可以直接去掉括号,原括号里各项符号都不变;
括号前是“- ”,去掉括号和它前面的“-”时,原括号里各项符号均要改变.
考点1 代数式
1. [2025长沙望城区期末]下列各式:; ;
;;; 中,是代数式的有
( )
B
A. 3个 B. 4个 C. 5个 D. 6个
【点拨】由代数式的定义可知,是代数式的有 ;
;; ,共4个.
返回
考点2 列代数式
2.如图,有一块长为18米,宽为10米的
长方形土地,现将三面留出宽都是
米的小路,余下的部分是
菜地,用含 的式子表示:
(1)菜地的长为__________米,宽为_________米;
(2)菜地的面积为_________________平方米.
返回
考点3 求代数式的值
3. 如果代数式 的值是7,那么代数
式 的值等于( )
D
A. 2 B. 3 C. D. 15
【点拨】因为 ,所以
.
返回
考点4 整式的相关概念
4.下列各式:,,,,,
,, 中,是整式的有______________,
是单项式的有________,是多项式的有________.(填序号)
①②③④⑥⑦
①②⑥
③④⑦
5.已知,均为有理数,
是关于的二次三项式,则 ___.
0
返回
6.若关于,的单项式与 的系数、次数均相同,
求, 的值.
【解】因为关于,的单项式与 的系数、次数
均相同,
所以,,解得, .
返回
考点5 同类项及合并同类项
7. [2025深圳月考]若单项式与 是同类项,
则 的值是( )
A
A. B. 0 C. 1 D. 2 025
【点拨】由题意,得,,所以 ,所以
.
返回
8. 下列化简正确的是( )
D
A. B.
C. D.
返回
考点6 整式的加减
9.[2025北京师大附中月考]先化简,再求值:
,其中, .
【解】
.
当, 时,原式
.
返回
10. 已知 ,小明同
学错将“”看成“ ”,算得的结果为
.
(1)求 ;
【解】因为 ,
,
所以
.
(2)求 .
.
返回
考点7 整式加减的应用
11. 一粥一饭,当思来之不易;半丝半缕,恒念
物力维艰.为了让同学们养成良好的节约习惯,学生会倡导的
勤工俭学活动效果显著,每个班级把本班的废弃试卷、书本
进行分类整理,每周把废品统一卖出,钱款用于班级日常开
支,上周七年级一班收入 元,二班收入比一班收入的2倍少
80元,三班收入比二班收入的一半多100元.
(1)用含 的式子表示三个班的上周总收入;
【解】三个班的上周总收入是
(元).
(2)当 时,求三个班的上周总收入.
当 时,
三个班的上周总收入是 (元).
返回
12.如图是2025年12月的日历.
(1)带阴影的十字框中的5个数之和
与十字框中心的数有什么关系?
【解】带阴影的十字框中的5个数之和
是十字框中心的数的5倍.
(2)不改变十字框的大小,如果将带阴影的十字框移至其
他几个位置,你能得出什么结论?你知道为什么吗?
带阴影的十字框中的5个数之和是十字
框中心的数的5倍,理由如下:设十字
框中心的数为 ,则其余4个数分别为
,,, ,所以带阴影的
十字框中的5个数之和为
所以带阴影的十字框中的5个数之和是十字框中心的数的5倍.
,
(3)这个结论对于任何一个月的日历都成立吗?
这个结论对于任何一个月的日历都成立.
返回
考点8 规律探究
13. 莫高窟坐落于河西
走廊西部的尽头——敦煌,是我国古
29
代文明的璀璨艺术宝库.莫高窟保存壁画4.5万多平方米,具
有独特的形式美感和艺术魅力.小明发现,壁画纹样中还蕴藏
着数学知识,如图,第①个图案中有5个花朵图案,第②个图
案中有8个花朵图案,第③个图案中有11个花朵图案, ,
按此规律排列下去,则第⑨个图案中花朵图案的个数为____.
【点拨】由题知,第①个图案
中有 (个)花朵
图案,第②个图案中有 (个)花朵图案,第③
个图案中有(个)花朵图案, ,依此规律,
第 个图案中有 (个)花朵图案,
所以第⑨个图案中花朵图案的个数为 .
返回
思想1 分类讨论思想
14.已知与的和是单项式,是常数,求,
的值或取值范围.
【解】由题意分以下两种情况讨论:
(1)当时, 可取任意数;
(2)当 时,由已知可得两个单项式为同类项,则
,解得 .
综上所述,,取任意数或, .
返回
思想2 整体思想
15. 已知, ,则
的值是( )
D
A. 18 B. 19 C. 20 D. 21
返回
思想3 数形结合思想
16. 有理数,,, 在数轴上对应点的位置如图所示,
若 ,则
的值是( )
B
A. 77 B. 78 C. D.
【点拨】由数轴可得 ,
所以,, .
所以
.
所以 .
所以
.
返回
谢谢观看!
同课章节目录
