第4章 图形的认识【章末复习】 课件(共34张PPT)
文档属性
| 名称 | 第4章 图形的认识【章末复习】 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 08:01:06 | ||
图片预览






文档简介
(共34张PPT)
章末复习
第4章 图形的认识
【2024新教材】湘教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第 4 章 图形的认识章末复习
在第 4 章 “图形的认识” 的学习中,我们探索了丰富的图形世界,从立体图形到平面图形,从线段、射线、直线到角的相关知识,这些内容构成了几何学习的重要基础。接下来,我们对本章知识进行系统复习,加深理解与掌握,为后续学习做好准备。
一、知识框架梳理
(一)立体图形与平面图形
立体图形:各部分不都在同一平面内,具有长、宽、高三个维度,如长方体、正方体、圆柱、圆锥、球等 。长方体有 6 个面、12 条棱、8 个顶点;圆柱由两个底面(圆形)和一个侧面(曲面)组成;圆锥有一个底面(圆形)和一个侧面(展开为扇形) 。
平面图形:所有点都在同一平面内,只有长和宽两个维度,常见的有三角形、四边形(长方形、正方形、梯形等)、圆形等 。三角形按角分为锐角三角形、直角三角形、钝角三角形;按边分为等边三角形、等腰三角形、不等边三角形 。
两者联系:立体图形可通过视图、展开图等方式得到平面图形;一些平面图形经过折叠、旋转能形成立体图形 。
(二)线段、射线、直线
图形
端点个数
长度是否可测量
延伸性
表示方法示例
线段
2 个
可测量
无
线段 AB、线段 a
射线
1 个
不可测量
向一端无限延伸
射线 OA
直线
0 个
不可测量
向两端无限延伸
直线 AB、直线 l
(三)角相关知识
角的定义与表示:由两条具有公共端点的射线组成或一条射线绕端点旋转形成;表示方法有三个大写字母(如∠AOB)、一个大写字母(顶点处只有一个角时,如∠O)、数字或希腊字母(如∠1、∠α) 。
角的分类:锐角(大于 0° 小于 90°)、直角(等于 90°)、钝角(大于 90° 小于 180°)、平角(等于 180°)、周角(等于 360°) 。
角的度量与计算:度量单位有度、分、秒,1° = 60',1' = 60'';计算时度、分、秒分别进行加减乘运算,满 60 进 1,不够减借 1 当 60 。
余角和补角:两角和为 90° 互为余角,和为 180° 互为补角;同角或等角的余角、补角分别相等 。
二、重点知识回顾与典型例题
(一)立体图形的展开与折叠
例 1:一个正方体的表面展开图如图所示,在原正方体中,与 “祝” 字所在面相对的面上的字是( )
[此处可插入正方体展开图示例]
A. 考
B. 试
C. 顺
D. 利
解析:根据正方体展开图的 “相间、Z 端是对面” 规律,可判断出与 “祝” 字所在面相对的面上的字是 “利”。答案选 D。
(二)线段的计算
例 2:已知线段 AB = 8cm,点 C 在线段 AB 上,且 AC = 3cm,求 BC 的长度。
解析:因为 BC = AB - AC,已知 AB = 8cm,AC = 3cm,所以 BC = 8 - 3 = 5cm 。
(三)角的计算
例 3:已知∠α = 35°20',求∠α 的余角和补角的度数。
解析:∠α 的余角 = 90° - 35°20' = 89°60' - 35°20' = 54°40';∠α 的补角 = 180° - 35°20' = 179°60' - 35°20' = 144°40' 。
三、易错点剖析
立体图形展开图判断错误:对正方体等立体图形的多种展开图形式不熟悉,无法正确判断相对面 。复习时可多动手操作展开和折叠正方体模型,加深对展开图规律的理解 。
线段、射线、直线概念混淆:例如误认为射线可以测量长度,或者在表示时不注意端点位置和字母顺序 。要牢记三种图形的本质区别,多做概念辨析题 。
角的计算错误:在度、分、秒的换算和计算过程中出错,尤其是在涉及借位和进位时 。计算时要细心,可分步进行换算和计算,计算后进行检查 。
余角和补角性质应用不当:在复杂图形中,不能准确找出同角或等角的余角、补角,导致错误运用性质 。解题时要认真分析图形,标记出已知角和所求角,明确角之间的关系 。
通过本次复习,我们对第 4 章 “图形的认识” 的知识进行了全面回顾和巩固。希望同学们针对自己的薄弱环节,加强练习,熟练掌握这些知识,为后续学习更深入的几何内容打下坚实基础。如果在复习过程中还有疑问,欢迎随时交流探讨。
这份复习资料梳理了本章核心内容与要点。你若觉得某些部分的讲解深度不够,或想增加更多例题,欢迎随时提出,我们进一步完善。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
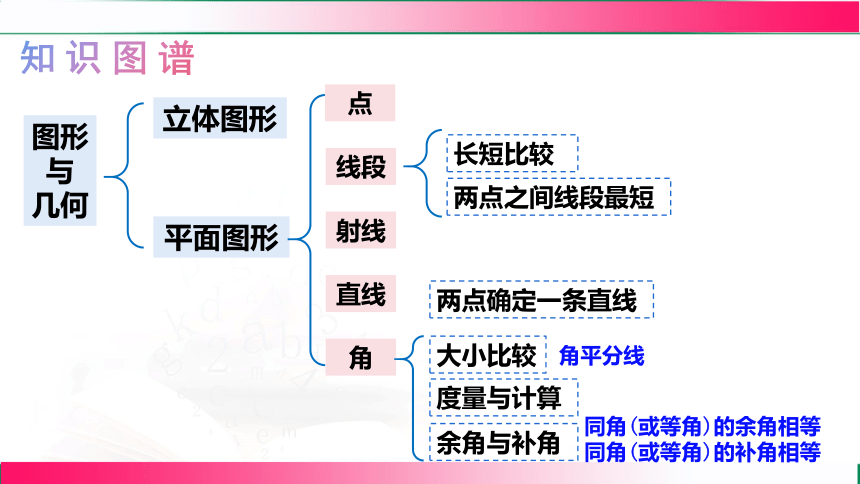
知识图谱
图形与
几何
立体图形
平面图形
直线
射线
角
线段
两点确定一条直线
长短比较
两点之间线段最短
度量与计算
大小比较
余角与补角
角平分线
同角(或等角)的余角相等
同角(或等角)的补角相等
点
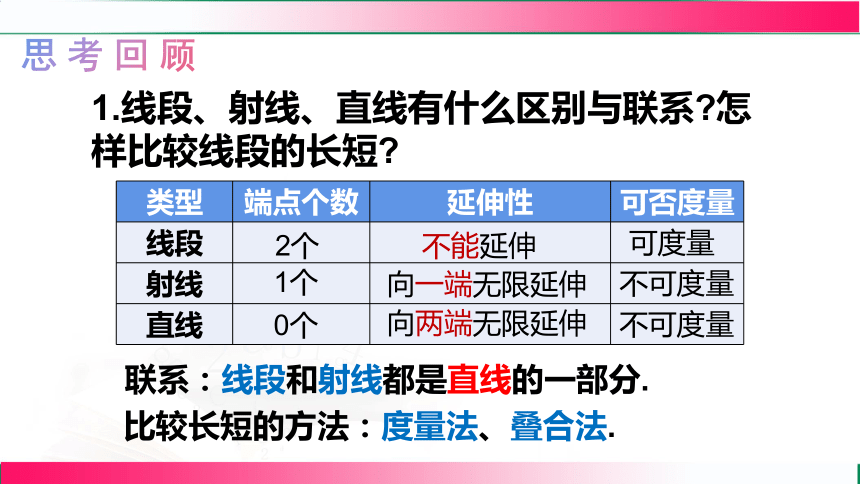
思考回顾
1.线段、射线、直线有什么区别与联系 怎样比较线段的长短
类型 端点个数 延伸性 可否度量
线段
射线
直线
2个
1个
0个
不能延伸
向一端无限延伸
向两端无限延伸
不可度量
不可度量
可度量
联系:线段和射线都是直线的一部分.
比较长短的方法:度量法、叠合法.
2.什么样的图形是角
把一条射线绕着它的端点从一个位置旋转到另一个位置时所成的图形叫作角.
有公共端点的两条射线组成的图形,叫作角.
动态定义:
静态定义:
3.角的大小用什么单位表示 怎样比较两个角的大小
比较角大小的方法:度量法、叠合法、尺规作图法.
度、分、秒.
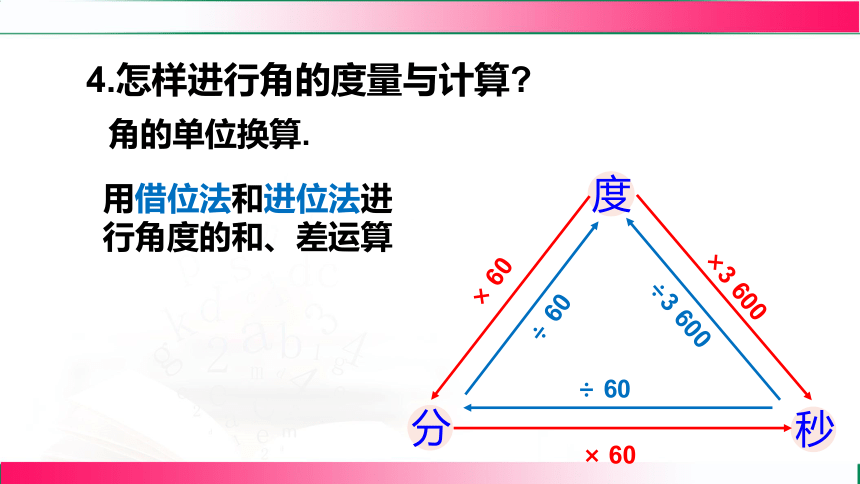
4.怎样进行角的度量与计算
用借位法和进位法进行角度的和、差运算
度
分
秒
× 60
×3 600
× 60
÷3 600
÷ 60
÷ 60
角的单位换算.
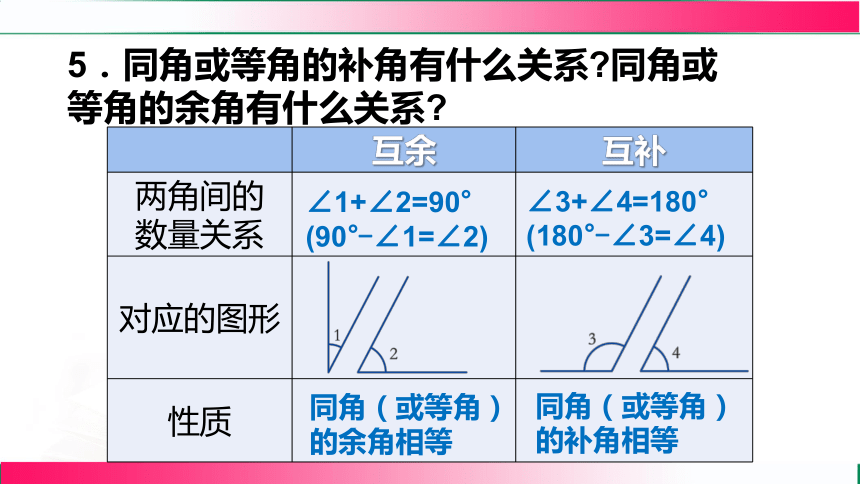
5.同角或等角的补角有什么关系 同角或等角的余角有什么关系
互余 互补
两角间的 数量关系
对应的图形
性质
∠1+∠2=90°
(90°-∠1=∠2)
∠3+∠4=180°
(180°-∠3=∠4)
同角(或等角)的余角相等
同角(或等角)的补角相等
为了区分有公共顶点的几个角,一般用三个大写字母表示角.
角的大小由始边绕顶点旋转到终边位置的旋转量确定,与所画角的边的长短无关(角的边是两条射线).
角的度、分、秒之间的换算是六十进制.
如果没有特别说明,本书中所讲的角只限于不大于平角的角.
注意事项
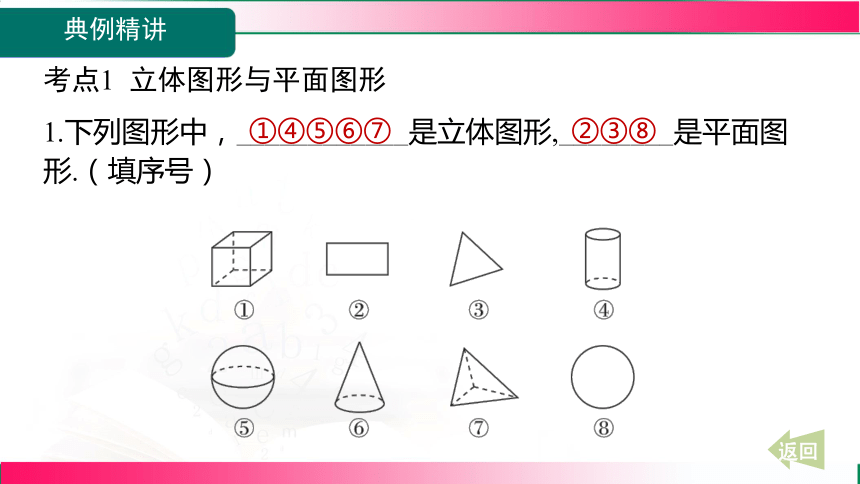
考点1 立体图形与平面图形
1.下列图形中,____________是立体图形,________是平面图
形.(填序号)
①④⑤⑥⑦
②③⑧
返回
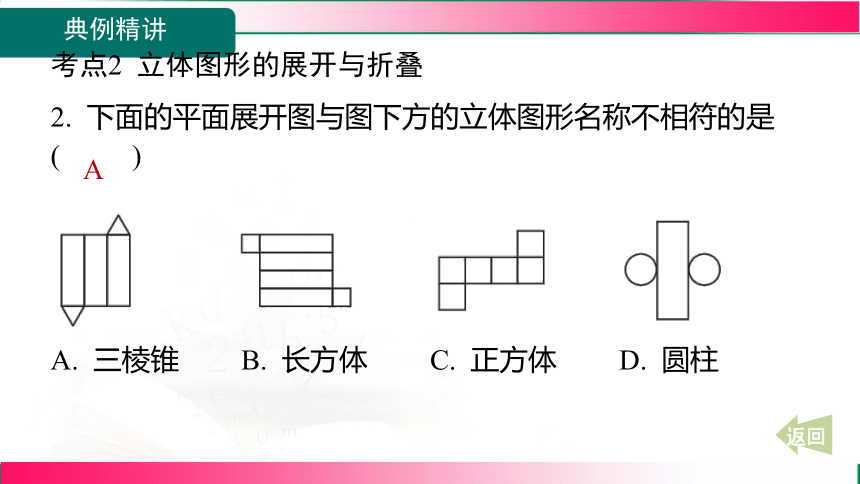
考点2 立体图形的展开与折叠
2. 下面的平面展开图与图下方的立体图形名称不相符的是
( )
A
A. 三棱锥
B. 长方体
C. 正方体
D. 圆柱
返回
(第3题)
3. 如图,正方体的表面展
开图上写有“我们热爱中国”六个字,还原成
正方体后“我”的对面的字是( )
B
A. 热 B. 爱 C. 中 D. 国
返回
(第4题)
4. [2024德阳]走马灯,又称仙音烛,据史料记
载,走马灯的历史起源于隋唐时期,盛行于宋代,
是中国特色工艺品,常见于除夕、元宵、中秋等节
日.在一次综合实践活动中,一同学用如图所示的
纸片,沿折痕折合成一个棱锥形的
A
A. 吉如意 B. 意吉如
C. 吉意如 D. 意如吉
“走马灯”,正方形做底,侧面有一个三角形面上写了“祥”字,当灯
旋转时,正好看到“吉祥如意”的字样,则在A,B,C处依次写上的字可
以是 ( )
返回
考点3 直线、射线、线段
5. 已知三点,,,画直线、画射线、连接 ,按
照上述语句画图正确的是( )
D
A. B. C. D.
返回
6. 岳麓山古镇,作为湖南的重
要景点,承载着丰富的历史文化,散发着古
韵质朴的气息,如同一幅见证时光变换的风
情画卷.为了游客的便利,某十字路口设有俯
两点之间线段最短
视示意图如图.若想走近路,在从位置到位置 的两条路径“
”和“ ”中,你会选择路径_______,选择的依
据是__________________.
返回
考点4 线段的计算
7.如图,已知和 的公共部
,
分,线段,的中点分别为, ,
,则, 的长分别为______________.
【点拨】因为 ,所以
.因为是 的中点,所以
.因为是 的中点,所以
,所以 . 所以
,所以
,所以 .
返回
8.如图,已知线段,延长到点,使得 ,点
为的中点,为的中点,若,求线段 的长度.
【解】因为, ,
所以 .
因为点为的中点,为 的中点,
所以, .
所以 .
返回
考点5 角的计算
9. 2025年4月24日17时17分神舟二十号载
人飞船在酒泉卫星发射中心发射成功.此时分针与时针夹角的
度数是______.
返回
10.[2025淮北期末]如图,已知直线与相交于点 ,
,分别是, 的平分线.
(1) 的补角是______________;
或
(2)若 ,求和 的度数.
【解】因为是 的平分线,
,
所以 ,
,
所以 .
因为是 的平分线,
所以
.
返回
思想1 方程思想
11.如图,点,,将线段分成的四部分, ,
,,分别是线段,,,的中点,且 ,
求线段 的长度.
【解】由题意设,,, .
因为,分别是,的中点,所以 ,
.
所以 ,
整理得,解得 .
又因为,分别是, 的中点,
所以
返回
思想2 数形结合思想
12.如图,这是一个无盖长方体盒子的表面展
开图(重叠部分不计),求这个盒子的容积.
【解】由题图易知,长方体盒子的长、宽、高分别是3,2,
1, 所以这个盒子的容积为6.
返回
思想3 分类讨论思想
13. 已知
, 的余角为
,的补角为,平分 ,
平分 .
(1)如图,当 ,且射线在 的外部时,用直
尺、量角器画出射线, 的准确位置;
【解】作射线, 如图①②所示.
(2)求(1)中 的度数,要求写出计算过程;
因为 , 的余角为
,的补角为 ,
所以 ,
.
又因为平分,平分 ,
所以 ,
.
分两种情况:
①当位于 下方时,如图①,
.
②当位于 上方时,如图②,
.
综上,的度数为 或 .
(3)当射线在的内部时,用含 的式子表示
的度数(直接写出结果).
或 .
返回
谢谢观看!
章末复习
第4章 图形的认识
【2024新教材】湘教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第 4 章 图形的认识章末复习
在第 4 章 “图形的认识” 的学习中,我们探索了丰富的图形世界,从立体图形到平面图形,从线段、射线、直线到角的相关知识,这些内容构成了几何学习的重要基础。接下来,我们对本章知识进行系统复习,加深理解与掌握,为后续学习做好准备。
一、知识框架梳理
(一)立体图形与平面图形
立体图形:各部分不都在同一平面内,具有长、宽、高三个维度,如长方体、正方体、圆柱、圆锥、球等 。长方体有 6 个面、12 条棱、8 个顶点;圆柱由两个底面(圆形)和一个侧面(曲面)组成;圆锥有一个底面(圆形)和一个侧面(展开为扇形) 。
平面图形:所有点都在同一平面内,只有长和宽两个维度,常见的有三角形、四边形(长方形、正方形、梯形等)、圆形等 。三角形按角分为锐角三角形、直角三角形、钝角三角形;按边分为等边三角形、等腰三角形、不等边三角形 。
两者联系:立体图形可通过视图、展开图等方式得到平面图形;一些平面图形经过折叠、旋转能形成立体图形 。
(二)线段、射线、直线
图形
端点个数
长度是否可测量
延伸性
表示方法示例
线段
2 个
可测量
无
线段 AB、线段 a
射线
1 个
不可测量
向一端无限延伸
射线 OA
直线
0 个
不可测量
向两端无限延伸
直线 AB、直线 l
(三)角相关知识
角的定义与表示:由两条具有公共端点的射线组成或一条射线绕端点旋转形成;表示方法有三个大写字母(如∠AOB)、一个大写字母(顶点处只有一个角时,如∠O)、数字或希腊字母(如∠1、∠α) 。
角的分类:锐角(大于 0° 小于 90°)、直角(等于 90°)、钝角(大于 90° 小于 180°)、平角(等于 180°)、周角(等于 360°) 。
角的度量与计算:度量单位有度、分、秒,1° = 60',1' = 60'';计算时度、分、秒分别进行加减乘运算,满 60 进 1,不够减借 1 当 60 。
余角和补角:两角和为 90° 互为余角,和为 180° 互为补角;同角或等角的余角、补角分别相等 。
二、重点知识回顾与典型例题
(一)立体图形的展开与折叠
例 1:一个正方体的表面展开图如图所示,在原正方体中,与 “祝” 字所在面相对的面上的字是( )
[此处可插入正方体展开图示例]
A. 考
B. 试
C. 顺
D. 利
解析:根据正方体展开图的 “相间、Z 端是对面” 规律,可判断出与 “祝” 字所在面相对的面上的字是 “利”。答案选 D。
(二)线段的计算
例 2:已知线段 AB = 8cm,点 C 在线段 AB 上,且 AC = 3cm,求 BC 的长度。
解析:因为 BC = AB - AC,已知 AB = 8cm,AC = 3cm,所以 BC = 8 - 3 = 5cm 。
(三)角的计算
例 3:已知∠α = 35°20',求∠α 的余角和补角的度数。
解析:∠α 的余角 = 90° - 35°20' = 89°60' - 35°20' = 54°40';∠α 的补角 = 180° - 35°20' = 179°60' - 35°20' = 144°40' 。
三、易错点剖析
立体图形展开图判断错误:对正方体等立体图形的多种展开图形式不熟悉,无法正确判断相对面 。复习时可多动手操作展开和折叠正方体模型,加深对展开图规律的理解 。
线段、射线、直线概念混淆:例如误认为射线可以测量长度,或者在表示时不注意端点位置和字母顺序 。要牢记三种图形的本质区别,多做概念辨析题 。
角的计算错误:在度、分、秒的换算和计算过程中出错,尤其是在涉及借位和进位时 。计算时要细心,可分步进行换算和计算,计算后进行检查 。
余角和补角性质应用不当:在复杂图形中,不能准确找出同角或等角的余角、补角,导致错误运用性质 。解题时要认真分析图形,标记出已知角和所求角,明确角之间的关系 。
通过本次复习,我们对第 4 章 “图形的认识” 的知识进行了全面回顾和巩固。希望同学们针对自己的薄弱环节,加强练习,熟练掌握这些知识,为后续学习更深入的几何内容打下坚实基础。如果在复习过程中还有疑问,欢迎随时交流探讨。
这份复习资料梳理了本章核心内容与要点。你若觉得某些部分的讲解深度不够,或想增加更多例题,欢迎随时提出,我们进一步完善。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识图谱
图形与
几何
立体图形
平面图形
直线
射线
角
线段
两点确定一条直线
长短比较
两点之间线段最短
度量与计算
大小比较
余角与补角
角平分线
同角(或等角)的余角相等
同角(或等角)的补角相等
点
思考回顾
1.线段、射线、直线有什么区别与联系 怎样比较线段的长短
类型 端点个数 延伸性 可否度量
线段
射线
直线
2个
1个
0个
不能延伸
向一端无限延伸
向两端无限延伸
不可度量
不可度量
可度量
联系:线段和射线都是直线的一部分.
比较长短的方法:度量法、叠合法.
2.什么样的图形是角
把一条射线绕着它的端点从一个位置旋转到另一个位置时所成的图形叫作角.
有公共端点的两条射线组成的图形,叫作角.
动态定义:
静态定义:
3.角的大小用什么单位表示 怎样比较两个角的大小
比较角大小的方法:度量法、叠合法、尺规作图法.
度、分、秒.
4.怎样进行角的度量与计算
用借位法和进位法进行角度的和、差运算
度
分
秒
× 60
×3 600
× 60
÷3 600
÷ 60
÷ 60
角的单位换算.
5.同角或等角的补角有什么关系 同角或等角的余角有什么关系
互余 互补
两角间的 数量关系
对应的图形
性质
∠1+∠2=90°
(90°-∠1=∠2)
∠3+∠4=180°
(180°-∠3=∠4)
同角(或等角)的余角相等
同角(或等角)的补角相等
为了区分有公共顶点的几个角,一般用三个大写字母表示角.
角的大小由始边绕顶点旋转到终边位置的旋转量确定,与所画角的边的长短无关(角的边是两条射线).
角的度、分、秒之间的换算是六十进制.
如果没有特别说明,本书中所讲的角只限于不大于平角的角.
注意事项
考点1 立体图形与平面图形
1.下列图形中,____________是立体图形,________是平面图
形.(填序号)
①④⑤⑥⑦
②③⑧
返回
考点2 立体图形的展开与折叠
2. 下面的平面展开图与图下方的立体图形名称不相符的是
( )
A
A. 三棱锥
B. 长方体
C. 正方体
D. 圆柱
返回
(第3题)
3. 如图,正方体的表面展
开图上写有“我们热爱中国”六个字,还原成
正方体后“我”的对面的字是( )
B
A. 热 B. 爱 C. 中 D. 国
返回
(第4题)
4. [2024德阳]走马灯,又称仙音烛,据史料记
载,走马灯的历史起源于隋唐时期,盛行于宋代,
是中国特色工艺品,常见于除夕、元宵、中秋等节
日.在一次综合实践活动中,一同学用如图所示的
纸片,沿折痕折合成一个棱锥形的
A
A. 吉如意 B. 意吉如
C. 吉意如 D. 意如吉
“走马灯”,正方形做底,侧面有一个三角形面上写了“祥”字,当灯
旋转时,正好看到“吉祥如意”的字样,则在A,B,C处依次写上的字可
以是 ( )
返回
考点3 直线、射线、线段
5. 已知三点,,,画直线、画射线、连接 ,按
照上述语句画图正确的是( )
D
A. B. C. D.
返回
6. 岳麓山古镇,作为湖南的重
要景点,承载着丰富的历史文化,散发着古
韵质朴的气息,如同一幅见证时光变换的风
情画卷.为了游客的便利,某十字路口设有俯
两点之间线段最短
视示意图如图.若想走近路,在从位置到位置 的两条路径“
”和“ ”中,你会选择路径_______,选择的依
据是__________________.
返回
考点4 线段的计算
7.如图,已知和 的公共部
,
分,线段,的中点分别为, ,
,则, 的长分别为______________.
【点拨】因为 ,所以
.因为是 的中点,所以
.因为是 的中点,所以
,所以 . 所以
,所以
,所以 .
返回
8.如图,已知线段,延长到点,使得 ,点
为的中点,为的中点,若,求线段 的长度.
【解】因为, ,
所以 .
因为点为的中点,为 的中点,
所以, .
所以 .
返回
考点5 角的计算
9. 2025年4月24日17时17分神舟二十号载
人飞船在酒泉卫星发射中心发射成功.此时分针与时针夹角的
度数是______.
返回
10.[2025淮北期末]如图,已知直线与相交于点 ,
,分别是, 的平分线.
(1) 的补角是______________;
或
(2)若 ,求和 的度数.
【解】因为是 的平分线,
,
所以 ,
,
所以 .
因为是 的平分线,
所以
.
返回
思想1 方程思想
11.如图,点,,将线段分成的四部分, ,
,,分别是线段,,,的中点,且 ,
求线段 的长度.
【解】由题意设,,, .
因为,分别是,的中点,所以 ,
.
所以 ,
整理得,解得 .
又因为,分别是, 的中点,
所以
返回
思想2 数形结合思想
12.如图,这是一个无盖长方体盒子的表面展
开图(重叠部分不计),求这个盒子的容积.
【解】由题图易知,长方体盒子的长、宽、高分别是3,2,
1, 所以这个盒子的容积为6.
返回
思想3 分类讨论思想
13. 已知
, 的余角为
,的补角为,平分 ,
平分 .
(1)如图,当 ,且射线在 的外部时,用直
尺、量角器画出射线, 的准确位置;
【解】作射线, 如图①②所示.
(2)求(1)中 的度数,要求写出计算过程;
因为 , 的余角为
,的补角为 ,
所以 ,
.
又因为平分,平分 ,
所以 ,
.
分两种情况:
①当位于 下方时,如图①,
.
②当位于 上方时,如图②,
.
综上,的度数为 或 .
(3)当射线在的内部时,用含 的式子表示
的度数(直接写出结果).
或 .
返回
谢谢观看!
同课章节目录
