14.2三角形全等的判定 同步练习 (含解析)2025-2026学年人教版数学八年级上册
文档属性
| 名称 | 14.2三角形全等的判定 同步练习 (含解析)2025-2026学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 929.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-08 22:14:33 | ||
图片预览


文档简介
14.2三角形全等的判定 同步练习 2025-2026学年人教版数学八年级上册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.[2025河南郑州外国语学校分校·期末]下列条件中,不能作出唯一三角形的是( )
A.,, B.,,
C.,, D.,,
2.[2025陕西高新一中·期末]如图,已知,,下列条件中,无法判定的是( )
A. B. C. D.
3.[2025河南郑州外国语学校分校·期末]如图,在方格纸中,以为一边作,使之与全等,在方格的格点中找出符合条件的P点(不与点A,B,C重合),则点P有( )
A.1个 B.2个 C.3个 D.4个
4.[2025吉林长春市第二实验中学·月考]一名工作人员不慎将一块三角形模具打碎成了三块,如图所示,他是否可以只带其中的一块碎片到商店去,就能买一块与原来一模一样的三角形模具呢?答案是肯定的,那么他该带哪款去?( ).
A.不能 B.带① C.带② D.带③
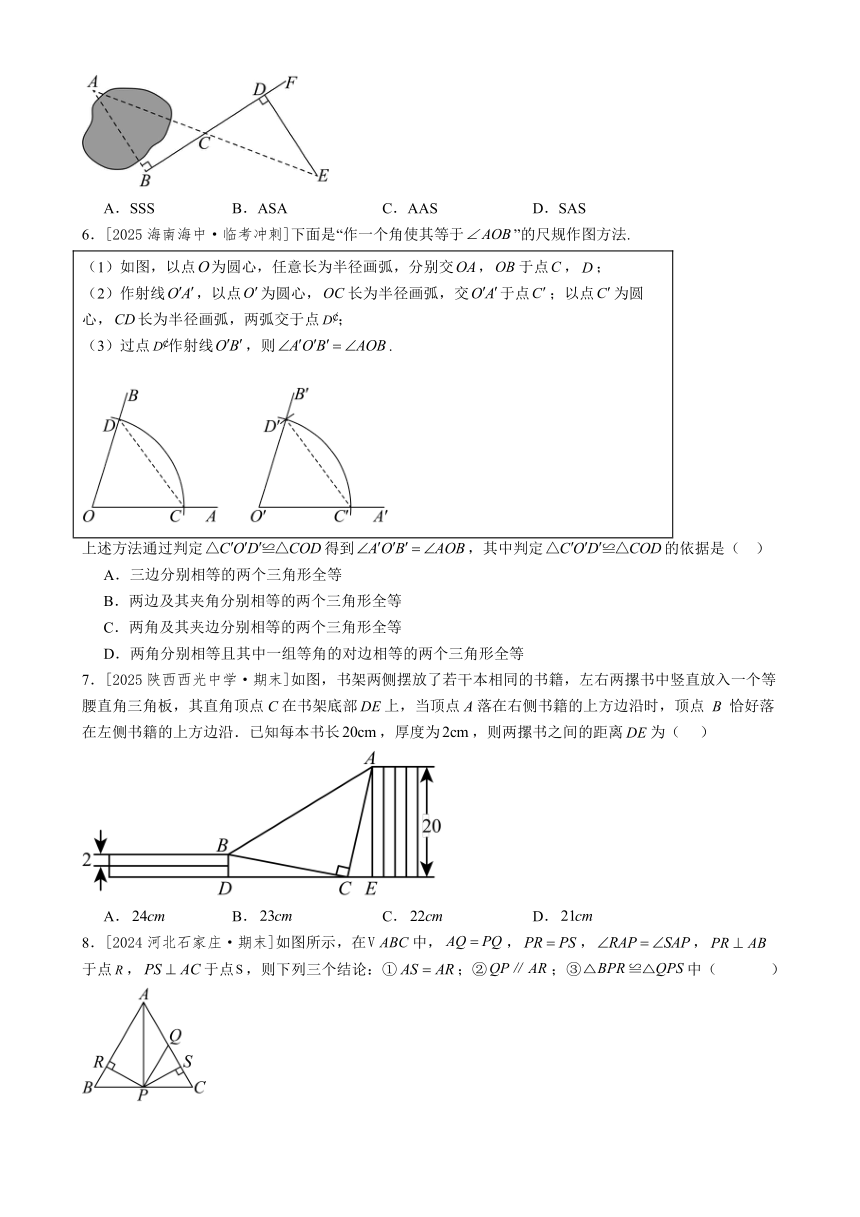
5.[2024宁夏银川·期末]如图,要测量池塘两岸相对的两点A,B的距离,小明在池塘外取的垂线上的点C,D,使,再画出的垂线,使E与A,C在一条直线上,这时测得的长就是的长,依据是( )
A.SSS B.ASA C.AAS D.SAS
6.[2025海南海中·临考冲刺]下面是“作一个角使其等于”的尺规作图方法.
(1)如图,以点为圆心,任意长为半径画弧,分别交,于点,; (2)作射线,以点为圆心,长为半径画弧,交于点;以点为圆心,长为半径画弧,两弧交于点; (3)过点作射线,则.
上述方法通过判定得到,其中判定的依据是( )
A.三边分别相等的两个三角形全等
B.两边及其夹角分别相等的两个三角形全等
C.两角及其夹边分别相等的两个三角形全等
D.两角分别相等且其中一组等角的对边相等的两个三角形全等
7.[2025陕西西光中学·期末]如图,书架两侧摆放了若干本相同的书籍,左右两摞书中竖直放入一个等腰直角三角板,其直角顶点C在书架底部上,当顶点A落在右侧书籍的上方边沿时,顶点 B 恰好落在左侧书籍的上方边沿.已知每本书长,厚度为,则两摞书之间的距离为( )
A. B. C. D.
8.[2024河北石家庄·期末]如图所示,在中,,,,于点,于点,则下列三个结论:①;②;③中( )
A.全部正确 B.仅①和②正确 C.仅①和正确 D.仅①和③正确
二、填空题
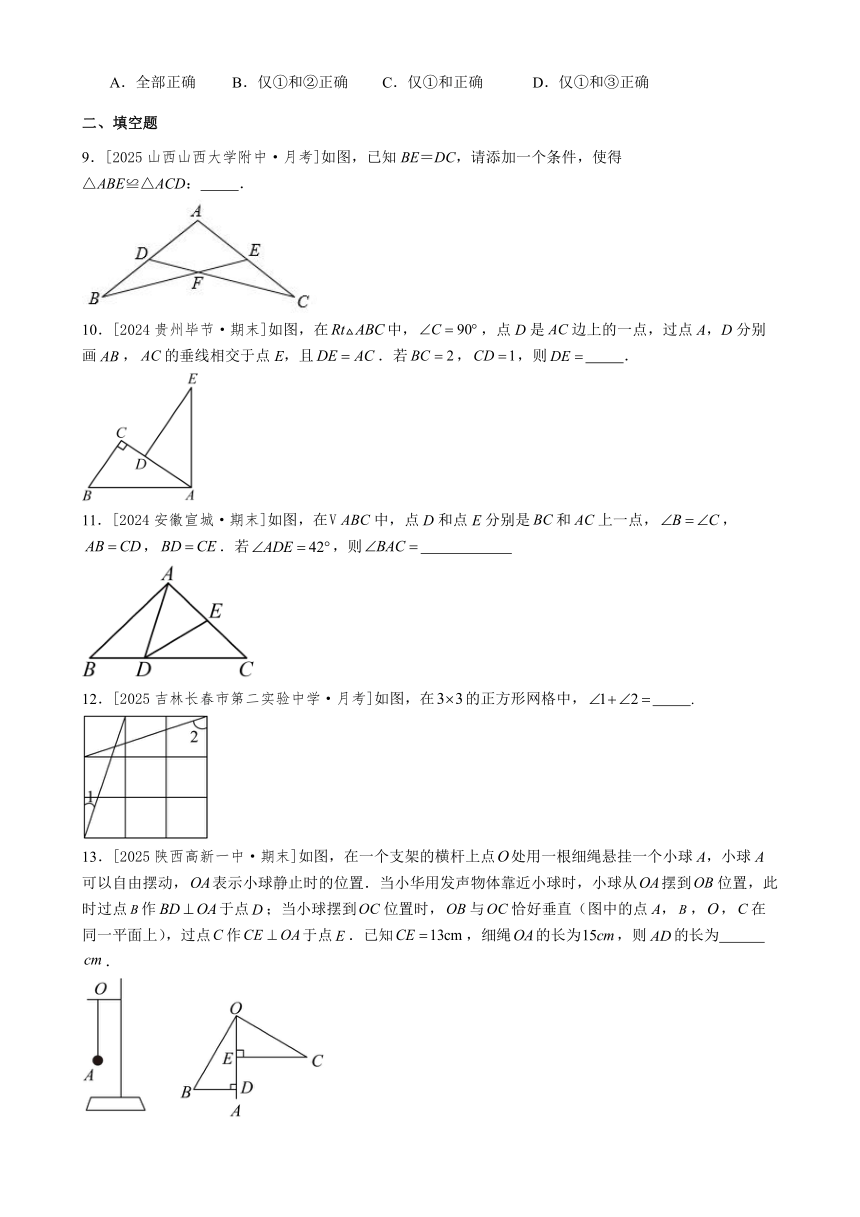
9.[2025山西山西大学附中·月考]如图,已知BE=DC,请添加一个条件,使得△ABE≌△ACD: .
10.[2024贵州毕节·期末]如图,在中,,点D是边上的一点,过点A,D分别画,的垂线相交于点E,且.若,,则 .
11.[2024安徽宣城·期末]如图,在中,点D和点E分别是和上一点,,,.若,则
12.[2025吉林长春市第二实验中学·月考]如图,在的正方形网格中, .
13.[2025陕西高新一中·期末]如图,在一个支架的横杆上点处用一根细绳悬挂一个小球A,小球A可以自由摆动,表示小球静止时的位置.当小华用发声物体靠近小球时,小球从摆到位置,此时过点作于点;当小球摆到位置时,与恰好垂直(图中的点A,,,在同一平面上),过点作于点.已知,细绳的长为,则的长为 .
14.[2025陕西西安市曲江第一中学·期中]如图,在中,,,过点作,且,则的面积为 .
三、解答题
15.[2025陕西西光中学·期中]已知:如图,,,,那么吗?请说明理由.
16.[2021湖北黄石·中考真题]如图,D是的边上一点,,交于点E,.
(1)求证:;
(2)若,,求的长.
17.[八年级·中考真题]已知:如图,在 和 中, , , , 在同一条直线上.下面四个条件: ; ; ; .
(1)请选择其中的三个条件,使得 (写出一种情况即可);
(2)在(1)的条件下,求证: .
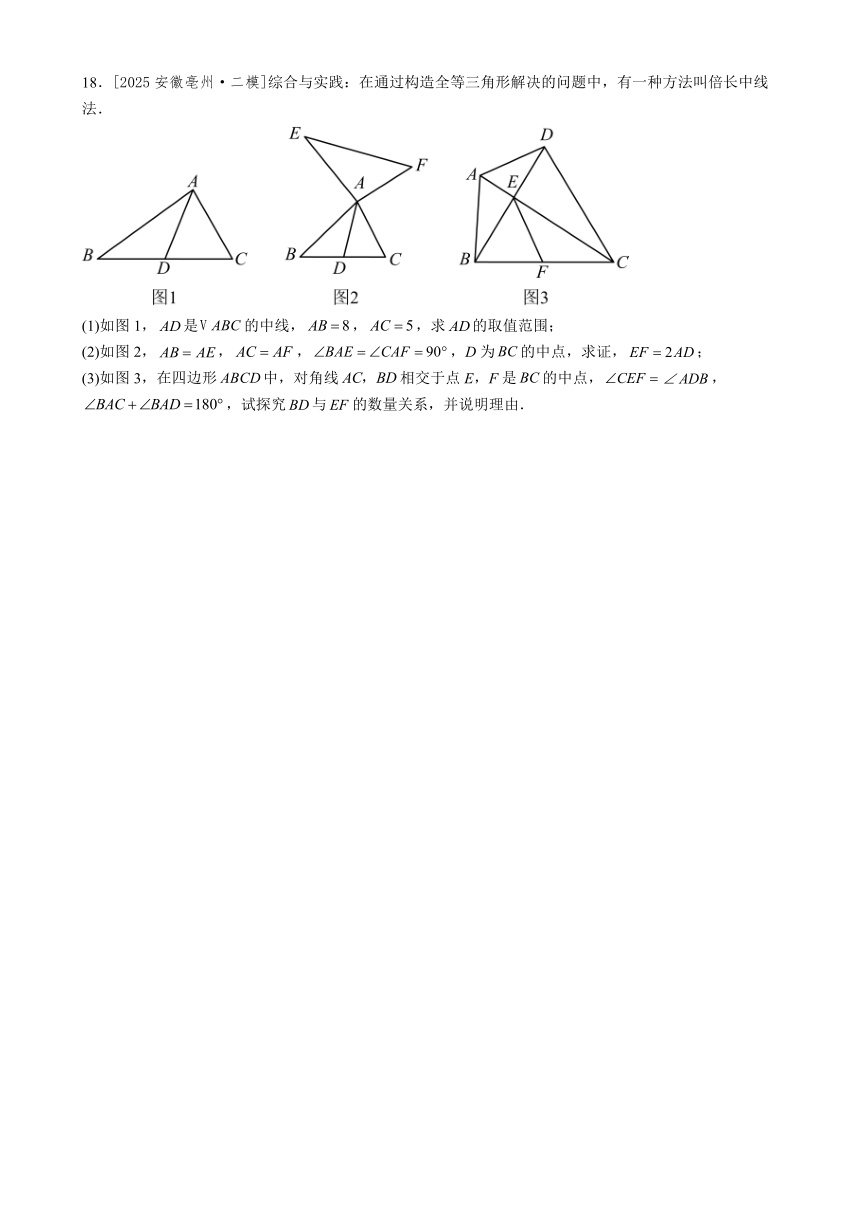
18.[2025安徽亳州·二模]综合与实践:在通过构造全等三角形解决的问题中,有一种方法叫倍长中线法.
(1)如图1,是的中线,,,求的取值范围;
(2)如图2,,,,D为的中点,求证,;
(3)如图3,在四边形中,对角线相交于点E,F是的中点,,,试探究与的数量关系,并说明理由.
参考答案
1.【答案】B
【分析】根据三角形全等判定定理逐项判断即可.
【详解】解:A.三边确定,则形状固定,所以可作唯一三角形,故该选项不符合题意;
B.并不是,的夹角,所以画出三角形不唯一,故该选项符合题意;
C.知两边长及其两边的夹角确定,可作唯一的三角形,故该选项不符合题意;
D.已知相邻两角以及相邻边,可作唯一三角形,故该选项不符合题意;
故选B.
2.【答案】D
【分析】由全等三角形的判定依次判断可求解.
【详解】A、添加,由“”可证,故选项A不符合题意;
B、添加,由“”可证,故选项B不符合题意;
C、添加,由“”可证,故选项C不符合题意;
D、添加,不能证明,故选项D符合题意;
故选D.
3.【答案】C
【分析】根据全等三角形的判定定理找出各个点即可.
【详解】解:如图所示:
与全等,共有,共3个.
故选C
4.【答案】D
【分析】根据全等三角形的判定方法结合图形判断出带③去.
【详解】由图形可知,③有完整的两角与夹边,根据“角边角”可以作出与原三角形全等的三角形,
所以,最省事的做法是带③去.
故选D.
5.【答案】B
【分析】全等三角形的判定定理有.
【详解】解:∵,
∴,
在和中,
,
∴,
∴,
∴依据是,
故选B.
6.【答案】A
【分析】根据基本作图中,判定三角形全等的依据是边边边,解答即可.
【详解】解:根据上述基本作图,可得,
故可得判定三角形全等的依据是边边边,
故选A.
7.【答案】A
【分析】根据题意得,,即可证明,则有,结合即可求得答案.
【详解】解:∵为等腰直角三角形,
∴,,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∵每本书长,厚度为,
∴,
∴.
故选A.
8.【答案】B
【分析】只要证明,推出,即可判断①;由,推出,以及,可得,即可判断②.根据在与中,只有,以及,即可判断③.
【详解】解:∵于点,于点
∴在和中,
,
∴,
∴,①正确;
∵,
∴,
∵,
∴,
∴,②正确,
在与中,只有,以及,
∴不能判断,故③错误;
故选B.
9.【答案】∠B=∠C
【分析】根据全等三角形的判定方法解答即可.
【详解】解:∵BE=DC,∠A=∠A,
∴根据AAS,可以添加∠B=∠C,使得△ABE≌△ACD.
10.【答案】3
【分析】利用等量代换可得,证明,可得,再利用求解即可.
【详解】解:∵,,
∴,,
∵在中,,
∴,
在和中,
,
∴,
∴,
∴.
11.【答案】/96度
【分析】先证出,根据全等三角形的性质可得,再根据三角形的外角性质可得,然后根据三角形的内角和定理求解即可得.
【详解】解:在和中,
,
∴,
∴,
又∵,,
∴,
∴,
∴.
12.【答案】
【分析】先证明,可得,即可得出答案.
【详解】解:如图所示,
∵,
∴,
∴.
∵,
∴.
13.【答案】2
【详解】解:∵,
,
又∵,,
,
,
∴,
在和中,
,
∴,
∴,
又∵,
∴.
14.【答案】
【详解】解:如图,过点作交延长线于点,
∵,,,
∴,,,
∴,
在和中,
,
∴
∴
15.【答案】相等,见解析
【分析】由,得,由,得,即可证,故.
【详解】解:相等,理由如下:
,
,即,
∵,
,
在和中,
,
,
.
16.【答案】(1)见详解
(2)1
【分析】(1)由平行线的性质可得,,再利用证明即可;
(2)由(1)可得,,即可得,即可求解.
【详解】(1)证明:∵,
∴,,
在和中,
,
∴;
(2)解:由(1)可得,,
∴,
∴.
17.【答案】
(1) 【解】根据题意,可以选择的条件为①②③或者①③④.
(2) 【证明】当选择的条件为①②③时, ,
,即 .在 和 中,
当选择的条件为①③④时, , ,即 .在 和 中, .
18.【答案】(1)
(2)见解析
(3),见解析
【分析】(1)根据可得,在中利用三角形的三边关系可求得,即可根据求解;
(2)延长至G,使,连接,先证明,得到,,再证明,即可得到;
(3)延长到G,使得,连接,延长到H,使得,连接,先证可得,,再证明,得到,,最后证明,得到.
【详解】(1)解:延长到点E.使,连接,
∵是的中线,
∴,又,
∴,
∴,
∵在中,,
∴,
∵,
∴,
∴,解得,
故答案为:;
(2)证明:延长至G,使,连接,则
∵点D为的中点,
∴,
在和中
,
∴,
∴,,
∵,
∴,
∵,
∴,
∴,
在和中
,
∴,
∴.
(3)证明:如图,延长到G,使得,连接,延长到H,使得,连接,
∵点F是边的中点,
∴,
∵,
∴,
∴,,
∴,
∴,
∵,
∴,
∵,
∴.
∴,,
∵,
∴,
∴,
∴.
第 page number 页,共 number of pages 页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.[2025河南郑州外国语学校分校·期末]下列条件中,不能作出唯一三角形的是( )
A.,, B.,,
C.,, D.,,
2.[2025陕西高新一中·期末]如图,已知,,下列条件中,无法判定的是( )
A. B. C. D.
3.[2025河南郑州外国语学校分校·期末]如图,在方格纸中,以为一边作,使之与全等,在方格的格点中找出符合条件的P点(不与点A,B,C重合),则点P有( )
A.1个 B.2个 C.3个 D.4个
4.[2025吉林长春市第二实验中学·月考]一名工作人员不慎将一块三角形模具打碎成了三块,如图所示,他是否可以只带其中的一块碎片到商店去,就能买一块与原来一模一样的三角形模具呢?答案是肯定的,那么他该带哪款去?( ).
A.不能 B.带① C.带② D.带③
5.[2024宁夏银川·期末]如图,要测量池塘两岸相对的两点A,B的距离,小明在池塘外取的垂线上的点C,D,使,再画出的垂线,使E与A,C在一条直线上,这时测得的长就是的长,依据是( )
A.SSS B.ASA C.AAS D.SAS
6.[2025海南海中·临考冲刺]下面是“作一个角使其等于”的尺规作图方法.
(1)如图,以点为圆心,任意长为半径画弧,分别交,于点,; (2)作射线,以点为圆心,长为半径画弧,交于点;以点为圆心,长为半径画弧,两弧交于点; (3)过点作射线,则.
上述方法通过判定得到,其中判定的依据是( )
A.三边分别相等的两个三角形全等
B.两边及其夹角分别相等的两个三角形全等
C.两角及其夹边分别相等的两个三角形全等
D.两角分别相等且其中一组等角的对边相等的两个三角形全等
7.[2025陕西西光中学·期末]如图,书架两侧摆放了若干本相同的书籍,左右两摞书中竖直放入一个等腰直角三角板,其直角顶点C在书架底部上,当顶点A落在右侧书籍的上方边沿时,顶点 B 恰好落在左侧书籍的上方边沿.已知每本书长,厚度为,则两摞书之间的距离为( )
A. B. C. D.
8.[2024河北石家庄·期末]如图所示,在中,,,,于点,于点,则下列三个结论:①;②;③中( )
A.全部正确 B.仅①和②正确 C.仅①和正确 D.仅①和③正确
二、填空题
9.[2025山西山西大学附中·月考]如图,已知BE=DC,请添加一个条件,使得△ABE≌△ACD: .
10.[2024贵州毕节·期末]如图,在中,,点D是边上的一点,过点A,D分别画,的垂线相交于点E,且.若,,则 .
11.[2024安徽宣城·期末]如图,在中,点D和点E分别是和上一点,,,.若,则
12.[2025吉林长春市第二实验中学·月考]如图,在的正方形网格中, .
13.[2025陕西高新一中·期末]如图,在一个支架的横杆上点处用一根细绳悬挂一个小球A,小球A可以自由摆动,表示小球静止时的位置.当小华用发声物体靠近小球时,小球从摆到位置,此时过点作于点;当小球摆到位置时,与恰好垂直(图中的点A,,,在同一平面上),过点作于点.已知,细绳的长为,则的长为 .
14.[2025陕西西安市曲江第一中学·期中]如图,在中,,,过点作,且,则的面积为 .
三、解答题
15.[2025陕西西光中学·期中]已知:如图,,,,那么吗?请说明理由.
16.[2021湖北黄石·中考真题]如图,D是的边上一点,,交于点E,.
(1)求证:;
(2)若,,求的长.
17.[八年级·中考真题]已知:如图,在 和 中, , , , 在同一条直线上.下面四个条件: ; ; ; .
(1)请选择其中的三个条件,使得 (写出一种情况即可);
(2)在(1)的条件下,求证: .
18.[2025安徽亳州·二模]综合与实践:在通过构造全等三角形解决的问题中,有一种方法叫倍长中线法.
(1)如图1,是的中线,,,求的取值范围;
(2)如图2,,,,D为的中点,求证,;
(3)如图3,在四边形中,对角线相交于点E,F是的中点,,,试探究与的数量关系,并说明理由.
参考答案
1.【答案】B
【分析】根据三角形全等判定定理逐项判断即可.
【详解】解:A.三边确定,则形状固定,所以可作唯一三角形,故该选项不符合题意;
B.并不是,的夹角,所以画出三角形不唯一,故该选项符合题意;
C.知两边长及其两边的夹角确定,可作唯一的三角形,故该选项不符合题意;
D.已知相邻两角以及相邻边,可作唯一三角形,故该选项不符合题意;
故选B.
2.【答案】D
【分析】由全等三角形的判定依次判断可求解.
【详解】A、添加,由“”可证,故选项A不符合题意;
B、添加,由“”可证,故选项B不符合题意;
C、添加,由“”可证,故选项C不符合题意;
D、添加,不能证明,故选项D符合题意;
故选D.
3.【答案】C
【分析】根据全等三角形的判定定理找出各个点即可.
【详解】解:如图所示:
与全等,共有,共3个.
故选C
4.【答案】D
【分析】根据全等三角形的判定方法结合图形判断出带③去.
【详解】由图形可知,③有完整的两角与夹边,根据“角边角”可以作出与原三角形全等的三角形,
所以,最省事的做法是带③去.
故选D.
5.【答案】B
【分析】全等三角形的判定定理有.
【详解】解:∵,
∴,
在和中,
,
∴,
∴,
∴依据是,
故选B.
6.【答案】A
【分析】根据基本作图中,判定三角形全等的依据是边边边,解答即可.
【详解】解:根据上述基本作图,可得,
故可得判定三角形全等的依据是边边边,
故选A.
7.【答案】A
【分析】根据题意得,,即可证明,则有,结合即可求得答案.
【详解】解:∵为等腰直角三角形,
∴,,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∵每本书长,厚度为,
∴,
∴.
故选A.
8.【答案】B
【分析】只要证明,推出,即可判断①;由,推出,以及,可得,即可判断②.根据在与中,只有,以及,即可判断③.
【详解】解:∵于点,于点
∴在和中,
,
∴,
∴,①正确;
∵,
∴,
∵,
∴,
∴,②正确,
在与中,只有,以及,
∴不能判断,故③错误;
故选B.
9.【答案】∠B=∠C
【分析】根据全等三角形的判定方法解答即可.
【详解】解:∵BE=DC,∠A=∠A,
∴根据AAS,可以添加∠B=∠C,使得△ABE≌△ACD.
10.【答案】3
【分析】利用等量代换可得,证明,可得,再利用求解即可.
【详解】解:∵,,
∴,,
∵在中,,
∴,
在和中,
,
∴,
∴,
∴.
11.【答案】/96度
【分析】先证出,根据全等三角形的性质可得,再根据三角形的外角性质可得,然后根据三角形的内角和定理求解即可得.
【详解】解:在和中,
,
∴,
∴,
又∵,,
∴,
∴,
∴.
12.【答案】
【分析】先证明,可得,即可得出答案.
【详解】解:如图所示,
∵,
∴,
∴.
∵,
∴.
13.【答案】2
【详解】解:∵,
,
又∵,,
,
,
∴,
在和中,
,
∴,
∴,
又∵,
∴.
14.【答案】
【详解】解:如图,过点作交延长线于点,
∵,,,
∴,,,
∴,
在和中,
,
∴
∴
15.【答案】相等,见解析
【分析】由,得,由,得,即可证,故.
【详解】解:相等,理由如下:
,
,即,
∵,
,
在和中,
,
,
.
16.【答案】(1)见详解
(2)1
【分析】(1)由平行线的性质可得,,再利用证明即可;
(2)由(1)可得,,即可得,即可求解.
【详解】(1)证明:∵,
∴,,
在和中,
,
∴;
(2)解:由(1)可得,,
∴,
∴.
17.【答案】
(1) 【解】根据题意,可以选择的条件为①②③或者①③④.
(2) 【证明】当选择的条件为①②③时, ,
,即 .在 和 中,
当选择的条件为①③④时, , ,即 .在 和 中, .
18.【答案】(1)
(2)见解析
(3),见解析
【分析】(1)根据可得,在中利用三角形的三边关系可求得,即可根据求解;
(2)延长至G,使,连接,先证明,得到,,再证明,即可得到;
(3)延长到G,使得,连接,延长到H,使得,连接,先证可得,,再证明,得到,,最后证明,得到.
【详解】(1)解:延长到点E.使,连接,
∵是的中线,
∴,又,
∴,
∴,
∵在中,,
∴,
∵,
∴,
∴,解得,
故答案为:;
(2)证明:延长至G,使,连接,则
∵点D为的中点,
∴,
在和中
,
∴,
∴,,
∵,
∴,
∵,
∴,
∴,
在和中
,
∴,
∴.
(3)证明:如图,延长到G,使得,连接,延长到H,使得,连接,
∵点F是边的中点,
∴,
∵,
∴,
∴,,
∴,
∴,
∵,
∴,
∵,
∴.
∴,,
∵,
∴,
∴,
∴.
第 page number 页,共 number of pages 页
同课章节目录
