【期末押题卷】湖北省武汉市2025-2026学年六年级上学期期末模拟数学预测卷人教版(含解析)
文档属性
| 名称 | 【期末押题卷】湖北省武汉市2025-2026学年六年级上学期期末模拟数学预测卷人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1005.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-08 10:23:13 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
湖北省武汉市2025-2026学年六年级上学期期末模拟数学预测卷
一.计算题(共3小题,满分28分)
1.(10分)直接写出得数。
1﹣1%=
7÷0.1%= 0.23= 24 0.125= 1
2.(8分)计算下面各题,能简算的要简算。
3.(10分)解方程。
70%x=5.6
二.填空题(共11小题,满分20分)
4.(4分)70: %= (填小数)
5.(1分)红花的枝数比黄花的枝数多,则红花是黄花的 .
6.(2分)0.625的倒数是 ,的是 。
7.(1分)栽一种树苗,成活率为94%到100%,为保证470棵树能成活,需要至少栽树苗 棵。
8.(4分)在横线里填上“>”“<”或“=”。
①3.5÷0.9 3.5 ②4.6÷0.02 4.6÷0.2 ③4.6 4.6×1.2
④3.6÷1.2 3.6 ⑤3.2÷0.1 3.2×10 ⑥83×0.87 83
9.(1分)加工一批零件,甲单独做需要8天完成,乙单独做需要6天完成,两人合作, 天能完成。
10.(1分)一个三角形的三个内角度数的比是1:3:1,这个三角形按角分是 三角形,按边分是 三角形。
11.(2分)花生油的出油率是36%,现在要榨900千克花生油,要花生 千克。
12.(2分)老师用圆规在黑板上画圆,圆规两脚之间的距离是3分米。所画的圆的直径是 分米,周长是 分米,面积是 平方分米。
13.(1分)把一个圆按如图切开,拼成近似的长方形,近似的长方形的周长比圆的周长长6厘米,圆的面积是 cm2。
14.(1分)根据如表所示中数的排列规律,算一算A= ,B= 。
2 3
5 21
3 4
7 40
4 5
9 65
5 6
A B
三.选择题(共10小题,满分20分,每小题2分)
15.(2分)小红原来每天22:00睡觉,6:00 起床。国家实行“双减”政策后,小红现在每天21:20睡觉,7:20 起床。现在的睡眠时间比原来增加了( )%。
A.5% B.10% C.20% D.25%
16.(2分)有两根绳子。如果第一根剪去,那么还剩米;如果第二根剪去米,那么还剩总长的。原来两根绳子相比较,( )
A.第一根长 B.第二根长
C.两根一样长 D.无法确定哪根长
17.(2分)某商店出售两种服装,售价都是600元,一件是时令服装,可赚20%,另一件是过时服装,要赔20%,就这两件服装而言,商店的收入情况是( )
A.赚了 B.赔了 C.不赚不赔 D.无法确定
18.(2分)3:7的前项加上6,要使比值不变,后项应( )
A.加6 B.乘3 C.乘2
19.(2分)用12米长的铁条做直径是5分米的圆形铁环,最多可做( )个。
A.8 B.7
C.一个都做不了
20.(2分)有四个三角形,各自的三个内角的度数之比如下。其中( )对应的三角形一定不是直角三角形。
A.2:3:5 B.1:2:3 C.1:1:2 D.1:3:5
21.(2分)钟面上分针长5厘米,分针尖端在60分钟内所走过的路程是( )厘米。
A.31.4 B.50.24 C.12.56
22.(2分)甲、乙两个圆直径的比是2:1,那么它们面积的比是( )
A.2:1 B.4:1 C.8:1
23.(2分)“一分钟仰卧起坐”是《国家学生体质健康标准》的测试项目之一。红星小学六年级1班和2班所有男生均进行了此项测试,两个班的男生人数一样多。如图是六年级1班和2班男生“一分钟仰卧起坐”的测试成绩统计图。
根据如图信息,1班学生认为自己班男生的成绩比2班好,以下三位同学的观点能说明1班男生成绩比2班好的是( )
淘气 笑笑 奇思
两个班男生人数一样多,1班男生只有1人不及格,而2班男生有2人不及格。 这次测试,1班男生的优秀率比2班男生的优秀率高。 这次测试,1班男生在及格、良好和优秀三个等级中的人数均比2班多。
A.只有淘气 B.只有笑笑
C.只有笑笑和奇思 D.只有淘气和笑笑
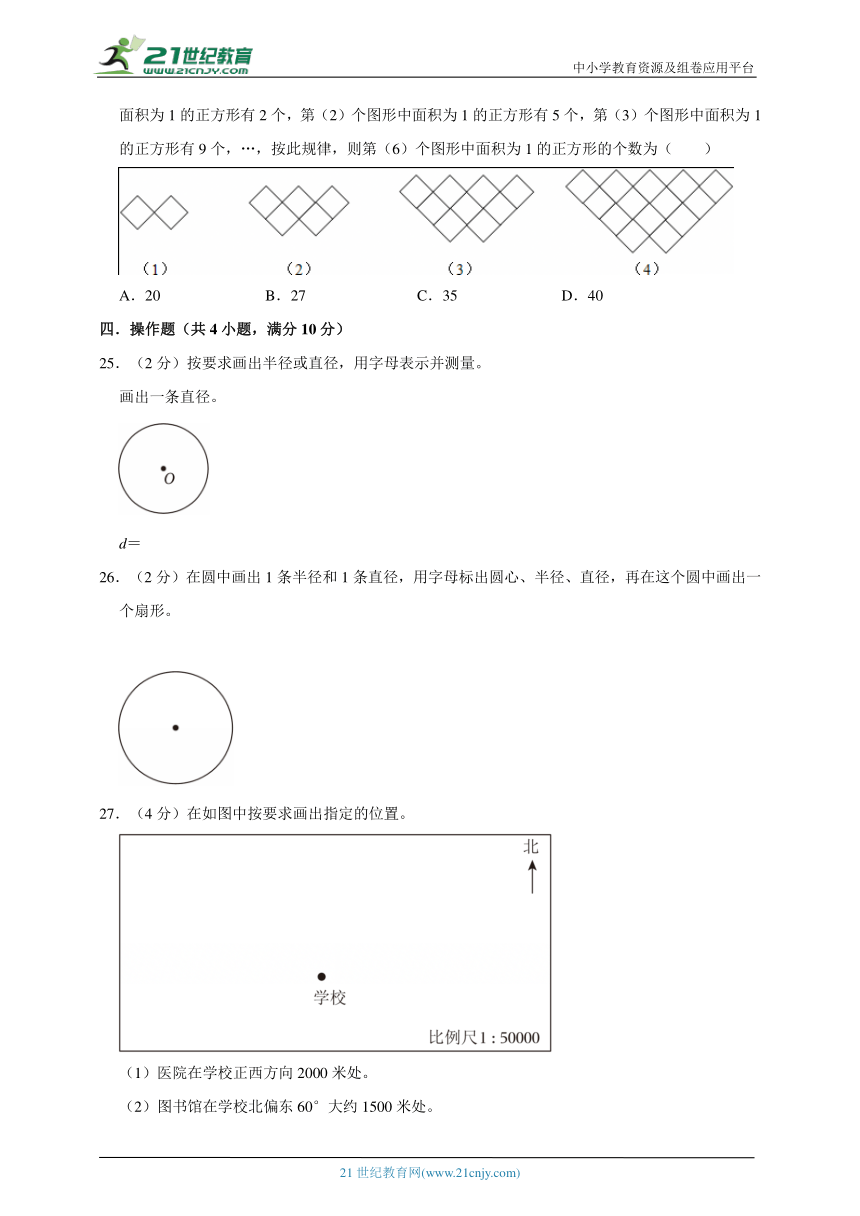
24.(2分)如图,下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,…,按此规律,则第(6)个图形中面积为1的正方形的个数为( )
A.20 B.27 C.35 D.40
四.操作题(共4小题,满分10分)
25.(2分)按要求画出半径或直径,用字母表示并测量。
画出一条直径。
d=
26.(2分)在圆中画出1条半径和1条直径,用字母标出圆心、半径、直径,再在这个圆中画出一个扇形。
27.(4分)在如图中按要求画出指定的位置。
(1)医院在学校正西方向2000米处。
(2)图书馆在学校北偏东60°大约1500米处。
(3)菜市场在图书馆南偏东45°大约1000米处。
28.(2分)手机作为现代化的通讯工具,给人们的生活带来了便利,为了更加合理的使用手机,实验小学社会实践调查小组以“你使用手机主要做什么”为主题,走进实验中学,对七年级学生进行了调查(每位同学只选择一项),并将结果分析整理,制成了下面两个统计图。其中:A.学习、B.通讯、C.娱乐、D.其他。
据以上信息请回答:
(1)本次调查共调查了 人,手机主要用来“通讯”的人占被调查人数的 %。
(2)手机主要用于“娱乐”的有 人。请将条形统计图补充完整。
(3)根据以上调查结果,你想对大家提出什么建议?
五.解答题(共6小题,满分22分)
29.(3分)两块铁皮,第一块的面积比第二块小,从两块铁皮上各剪下它们的,共剪下36平方分米.原来这两块铁皮的面积各是多少?
30.(4分)水稻最早发源于中国,然后才传入世界各地。历史上有文字可查的水稻亩产量数据从春秋时代起,发展到汉朝,平均亩产量达63千克,比春秋时期水稻亩产量增产26%。至唐朝实行灌溉田后,平均亩产量达138千克。历经千年发展到清朝,亩产量是唐朝的200%。新中国成立后,1958年达400千克,1964年袁隆平开始杂交水稻的研究之后,至2019年水稻亩产量达1500千克。新中国成立后,短短四五十年的时间,袁隆平教授通过科学种田让粮食产量翻倍提升,解决了全世界的吃饭问题,让中国人彻底端平了饭碗。
(1)春秋时期水稻亩产量是多少千克?
(2)清朝水稻亩产量是多少千克?
(3)2019年比1958年水稻亩产量提升了百分之几?
(4)要描述各个时期水稻亩产量的多少,选用 统计图比较合适;要描述各个时期水稻亩产量的变化情况选用 统计图比较合适。
31.(4分)学校计划绿化一块287平方米的空地,先划出种树,剩下的按2:3种花和草。种花和草的面积各是多少平方米?
32.(4分)只列式,不计算。
(1)某饲料加工厂5月份实际生产饲料5.5万吨,比计划多生产0.5万吨,比计划多生产百分之几?
(2)李阿姨把8000元钱存入银行,定期三年,年利率是2.35%。到期后李阿姨可得本息多少元?
(3)赵叔叔参加宿迁市半程马拉松比赛,小时跑千米。照这样的速度,他跑完21千米需要多少小时?
33.(3分)求如图中阴影部分的周长和面积。(单位:分米)
34.(4分)一块圆形铁皮和一块长方形铁皮的周长相等,已知长方形的长为9dm,宽为6.7dm,圆形铁皮的面积是多少?
湖北省武汉市2025-2026学年六年级上学期期末模拟数学预测卷
参考答案与试题解析
一.计算题(共3小题,满分28分)
1.(10分)直接写出得数。
1﹣1%=
7÷0.1%= 0.23= 24 0.125= 1
【考点】分数的四则混合运算;分数乘法;分数除法.
【专题】运算能力.
【答案】见试题解答内容
【分析】根据小数、分数、百分数加减乘除法以及四则混合运算的顺序,直接进行口算即可。
【解答】解:
1﹣1%=0.99
7÷0.1%=7000 0.23=0.008 2415 0.125=2 1
【点评】本题考查了简单的计算,计算时要细心,注意平时积累经验,提高计算的水平。
2.(8分)计算下面各题,能简算的要简算。
【考点】分数的四则混合运算;运算定律与简便运算.
【专题】运算能力.
【答案】;;66。
【分析】按照乘法分配律计算;
先算小括号里面的乘法,再算除法;
按照乘法分配律计算。
【解答】解:
( )
9
(98+1)
99
=66
【点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
3.(10分)解方程。
70%x=5.6
【考点】百分数方程求解;分数方程求解.
【专题】运算能力.
【答案】x=8;x=60。
【分析】根据等式的基本性质,方程两边同时除以70%。
先计算出方程左边xxx,再根据等式的性质,方程两边同时除以。
【解答】解:70%x=5.6
70%x÷70%=5.6÷70%
x=8
xx=15
x=15
x15
x=60
【点评】解方程的依据是等式的性质。解答过程要注意书写格式:上、下行等号对齐;不能连等。
二.填空题(共11小题,满分20分)
4.(4分)70: 56 125 %= 1.25 (填小数)
【考点】比与分数、除法的关系;小数、分数和百分数之间的关系及其转化.
【专题】数感.
【答案】56,125,1.25。
【分析】根据比与分数的关系5:4,再根据比的性质比的前、后项都乘14就是70:56;根据分数与除法的关系5÷4=1.25;把1.25的小数点向右移动两位添上百分号就是125%。
【解答】解:70:56125%=1.25
故答案为:56,125,1.25。
【点评】此题主要是考查小数、分数、比、百分数之间的关系及转化。利用它们之间的关系和性质进行转化即可。
5.(1分)红花的枝数比黄花的枝数多,则红花是黄花的 .
【考点】分数的四则混合运算.
【专题】综合填空题;文字叙述题.
【答案】见试题解答内容
【分析】红花的枝数比黄花的枝数多,把黄花的数量看作单位“1”,红花对应的分率是1,要求红花是黄花的几分之几,用红花的数量除以黄花的数量即可.
【解答】解:(1)÷1
1
答:红花是黄花的.
故答案为:.
【点评】此题考查了判断单位“1”的方法:一般是把“比、占、是、相当于”后面的量看作单位“1”.
6.(2分)0.625的倒数是 ,的是 。
【考点】倒数的认识;分数乘法.
【专题】综合填空题;应用意识.
【答案】;。
【分析】若两个数的乘积是1,我们就称这两个数互为倒数。分数乘以分数:用分子相乘的积作为分子,用分母相乘的积作为分母。
【解答】解:0.625的倒数是;
1
故答案为:;。
【点评】本题考查的主要内容是倒数的应用和分数乘法计算问题。
7.(1分)栽一种树苗,成活率为94%到100%,为保证470棵树能成活,需要至少栽树苗 500 棵。
【考点】百分率应用题.
【专题】应用题;应用意识.
【答案】500。
【分析】因为成活率=成活树苗的棵数÷栽树苗的总棵数×100%,要保证470棵树能成活,成活率就要按照最低的94%来计算,所以要栽树苗的棵数=成活的棵数÷成活率,即470÷94%,由此列式计算得出答案。
【解答】解:470÷94%
=470÷0.94
=500(棵)
答:需要至少栽树苗500棵。
故答案为:500。
【点评】此题的关键是根据“要栽树苗的棵数、成活的棵数、成活率”三者间的关系,求出要栽树苗的棵数。
8.(4分)在横线里填上“>”“<”或“=”。
①3.5÷0.9 > 3.5 ②4.6÷0.02 > 4.6÷0.2 ③4.6 < 4.6×1.2
④3.6÷1.2 < 3.6 ⑤3.2÷0.1 = 3.2×10 ⑥83×0.87 < 83
【考点】商的变化规律;积的变化规律.
【专题】综合判断题;运算能力.
【答案】>;>;<;<;=;<。
【分析】①一个数(0除外)除以小于1的数(0除外),商大于这个数,据此判断;
②计算后比较大小;
③一个数(0除外)乘大于1的数,积大于这个数,据此判断;
④一个数(0除外)除以大于1的数,商小于这个数,据此判断;
⑤除以一个数,等于乘这个数的倒数,据此判断;
⑥一个数(0除外)乘小于1的数,积小于这个数,据此判断。
【解答】解:①3.5÷0.9>3.5
②因为4.6÷0.02=230,4.6÷0.2=23,所以4.6÷0.02>4.6÷0.2
③4.6<4.6×1.2
④3.6÷1.2<3.6
⑤3.2÷0.1=3.2×10
⑥83×0.87<83
故答案为:>;>;<;<;=;<。
【点评】本题考查了积的变化规律和商的变化规律的应用。
9.(1分)加工一批零件,甲单独做需要8天完成,乙单独做需要6天完成,两人合作, 3 天能完成。
【考点】简单的工程问题.
【专题】应用题;应用意识.
【答案】3。
【分析】首先根据工作效率=工作量÷工作时间,把这批零件的工作量看成单位“1”,甲的工作效率是,乙的工作效率是,用工作总量除以合作的工作效率之和即可解答此题。
【解答】解:1÷()
=1
=3(天)
答:3天能完成。
故答案为:3。
【点评】此题考查儿了简单的工程问题。
10.(1分)一个三角形的三个内角度数的比是1:3:1,这个三角形按角分是 钝角 三角形,按边分是 等腰 三角形。
【考点】按比例分配应用题.
【专题】比和比例应用题;几何直观;运算能力;应用意识.
【答案】钝角,等腰。
【分析】根据三角形内角和定理,三角形三个内角之和是180°,这个三角形最大角占三个角度数的,根据分数乘法的意义,用180°乘就是这个三角形中最大角的度数。这个最大角如果是锐角,这个三角形就是锐角三角形;如果是直角,这个三角形就是直角三角形;如果是钝角,这个三角形就是钝角三角形。在三角形中相等的角所对的边相等,这个三角形中有两个角相等,就有两条边相等,根据等腰三角形的意义,此三角形是等腰三角形。
【解答】解:180°
=180°
=108°
这个三角形按角分是钝角三角形。
因为个三角形的三个内角度数的比是1:3:1
所以这个三角形中有两条边相等,按边分,这个三角形是等腰三角形
答:这个三角形按角分是钝角三角形,按边分是等腰三角形。
故答案为:钝角,等腰。
【点评】此题考查的知识点有:三角形内角和定理、按比例分配问题、三角形的分类等。
11.(2分)花生油的出油率是36%,现在要榨900千克花生油,要花生 2500 千克。
【考点】百分率应用题.
【专题】应用意识.
【答案】2500。
【分析】首先理解“出油率”的概念,出油率是指出油的重量占作物重量的百分比,即出油率100%,已知出油率是36%,现在要榨900千克花生油,求需要花生多少千克,用油的重量÷出油率,即900÷36%,计算即可。
【解答】解:900÷36%
=900÷0.36
=2500(千克)
答:要花生2500千克。
故答案为:2500。
【点评】此题考查了成活率的概念,熟练掌握是关键。
12.(2分)老师用圆规在黑板上画圆,圆规两脚之间的距离是3分米。所画的圆的直径是 6 分米,周长是 18.84 分米,面积是 28.26 平方分米。
【考点】圆、圆环的面积;圆、圆环的周长.
【专题】应用意识.
【答案】6,18.84,28.26。
【分析】根据直径与半径的关系,d=2r,圆的周长公式:C=2πr,圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:3×2=6(分米)
2×3.14×3=18.84(分米)
3.14×32
=3.14×9
=28.26(平方分米)
答:所画圆的直径是6分米,周长是18.84分米,面积是28.26平方分米。
故答案为:6,18.84,28.26。
【点评】此题主要考查圆的周长公式、圆的面积公式的灵活运用,关键是熟记公式。
13.(1分)把一个圆按如图切开,拼成近似的长方形,近似的长方形的周长比圆的周长长6厘米,圆的面积是 28.26 cm2。
【考点】圆与组合图形;圆、圆环的面积.
【专题】平面图形的认识与计算;空间观念.
【答案】28.26。
【分析】根据圆面积公式的推导过程可知,把一个圆剪拼成一个近似长方形,这个长方形的长等于圆周长的一半,长方形的宽等于圆的半径,拼成的长方形的周长比圆的周长增加了两条比较的长度,据此可以求出半径,根据圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:6÷2=3(厘米)
3.14×32
=3.14×9
=28.26(平方厘米)
答:圆的面积是28.26平方厘米。
故答案为:28.26。
【点评】此题考查的目的是理解掌握圆面积公式的推导过程及应用,圆的周长和圆的面积公式及应用。
14.(1分)根据如表所示中数的排列规律,算一算A= 11 ,B= 96 。
2 3
5 21
3 4
7 40
4 5
9 65
5 6
A B
【考点】数表中的规律.
【专题】压轴题;运算能力.
【答案】11,96。
【分析】规律:左下角的数依次加2,第一列的数字和乘右上角的数等于右下角的数。
【解答】解:A=9+2=11
B=(5+11)×6=96
故答案为:11,96。
【点评】本题考查了数表中的规律,关键是找到规律。
三.选择题(共10小题,满分20分,每小题2分)
15.(2分)小红原来每天22:00睡觉,6:00 起床。国家实行“双减”政策后,小红现在每天21:20睡觉,7:20 起床。现在的睡眠时间比原来增加了( )%。
A.5% B.10% C.20% D.25%
【考点】百分数的实际应用.
【专题】应用意识.
【答案】D
【分析】先用24时减去22时的差加上6时,求出小红原来的睡眠时间;再用24时减去21时20分的差加上7时20分,求出小红实行“双减”政策后的睡眠时间,最后求出现在的睡眠时间比原来增加了百分之几即可。
【解答】解:24时﹣22时+6时=8小时
24时﹣21时20分+7时20分=10小时
(10﹣8)÷8
=2÷8
=0.25
=25%
答:现在的睡眠时间比原来增加了25%。
故选:D。
【点评】解答本题需熟练掌握经历的时间的计算方法,明确求一个数比另一个数多百分之几的计算方法。
16.(2分)有两根绳子。如果第一根剪去,那么还剩米;如果第二根剪去米,那么还剩总长的。原来两根绳子相比较,( )
A.第一根长 B.第二根长
C.两根一样长 D.无法确定哪根长
【考点】分数除法应用题.
【专题】综合题;应用意识.
【答案】A
【分析】第一根绳子剪去,剩下的占第一根绳子长度的,还剩米。第二根绳子剪去米后,还剩总长的,则剪去的占第二根绳子长度的。根据已知比较量求单位“1”用除法计算,用比较量除以分率即可分别求出两根绳子原来的长度。最后进行比较即可。据此解答。
【解答】解:第一根绳子的长度:
=2(米)
第二根绳子的长度:
(米)
2,所以原来第一根绳子长。
故选:A。
【点评】已知一个数的几分之几是多少求这个数用除法计算。
17.(2分)某商店出售两种服装,售价都是600元,一件是时令服装,可赚20%,另一件是过时服装,要赔20%,就这两件服装而言,商店的收入情况是( )
A.赚了 B.赔了 C.不赚不赔 D.无法确定
【考点】百分数的实际应用.
【专题】应用意识.
【答案】B
【分析】把时令服装的进价看作单位“1”,则售价=进价×(1+20%);把过时服装的进价看作单位“1”,则售价=进价×(1﹣20%),求出两件服装的进价和与售价和进行比较即可。
【解答】解:600÷(1+20%)+600÷(1﹣20%)
=500+750
=1250(元)
600×2=1200(元)
1250>1200
答:就这两件服装而言,商店的收入情况是赔了。
故选:B。
【点评】本题主要考查百分数的实际应用,关键是利用进价与售价的数量关系做题。
18.(2分)3:7的前项加上6,要使比值不变,后项应( )
A.加6 B.乘3 C.乘2
【考点】比的性质.
【专题】推理能力.
【答案】B
【分析】3:7的前项加上6,即3+6=9,由3到9,扩大到原来的9÷3=3倍,要使比值不变,后项应扩大到原来的3倍,据此解答即可。
【解答】解:3+6=9
9÷3=3
所以把3:7的前项加上6,要使比值不变,后项应乘3。
故选:B。
【点评】此题考查比的性质的运用,比的前项和后项同时乘或除以相同的数(0除外),比值才不变。
19.(2分)用12米长的铁条做直径是5分米的圆形铁环,最多可做( )个。
A.8 B.7
C.一个都做不了
【考点】圆、圆环的周长.
【专题】几何直观.
【答案】B
【分析】先把单位进行换算,即12米=120分米,圆形铁环的周长=直径×π,然后用铁条的长度除以铁环的周长,把结果取整即可。
【解答】解:12米=120分米
5×3.14=15.7(分米)
120÷15.7≈7(个)
答:最多可以做7个。
故选:B。
【点评】此题主要考查圆的周长在实际生活中的应用。关键是知道用铁条的长度除以一个铁环的周长就是做的个数,结果要用去尾法取近似值。
20.(2分)有四个三角形,各自的三个内角的度数之比如下。其中( )对应的三角形一定不是直角三角形。
A.2:3:5 B.1:2:3 C.1:1:2 D.1:3:5
【考点】比的应用.
【专题】推理能力;应用意识.
【答案】D
【分析】根据直角三角形两个锐角的和等于直角,据此解答即可。
【解答】解:A.2+3=5,所以三角形三个内角度数之比为2:3:5的三角形是直角三角形。
B.1+2=3,所以三角形三个内角度数之比为1:2:3的三角形是直角三角形。
C.1+1=2,所以三角形三个内角度数之比为1:1:2的三角形是直角三角形。
D.1+3≠5,所以三角形三个内角度数之比为1:3:5的三角形不是直角三角形。
故选:D。
【点评】熟练掌握直角三角形的性质,是解答此题的关键。
21.(2分)钟面上分针长5厘米,分针尖端在60分钟内所走过的路程是( )厘米。
A.31.4 B.50.24 C.12.56
【考点】圆、圆环的周长.
【专题】应用意识.
【答案】A
【分析】60分钟分针针尖走过的路程是一个半径为5厘米圆的周长,根据圆周长的周长公式“C=2πr”,列式即可解答。
【解答】解:2×3.14×5
=6.28×5
=31.4(cm)
所以钟面上分针长5厘米,分针尖端在60分钟内所走过的路程是31.4厘米。
故选:A。
【点评】关键是掌握并灵活运用圆的周长公式。
22.(2分)甲、乙两个圆直径的比是2:1,那么它们面积的比是( )
A.2:1 B.4:1 C.8:1
【考点】圆、圆环的面积;比的应用.
【专题】应用意识.
【答案】B
【分析】根据直径与半径的关系,d=2r,甲、乙两个圆直径的比是2:1,则甲、乙两个圆半径的比是2:1,再根据圆的面积公式:S=πr2,因为圆周率是一定的,所以甲、乙两个圆面积的比等于半径平方的比。据此解答即可。
【解答】解:22:12=4:1
答:它们面积的比是4:1。
故选:B。
【点评】此题主要考查圆的面积公式的灵活运用,因数与积的变化规律及应用,比的意义及应用。
23.(2分)“一分钟仰卧起坐”是《国家学生体质健康标准》的测试项目之一。红星小学六年级1班和2班所有男生均进行了此项测试,两个班的男生人数一样多。如图是六年级1班和2班男生“一分钟仰卧起坐”的测试成绩统计图。
根据如图信息,1班学生认为自己班男生的成绩比2班好,以下三位同学的观点能说明1班男生成绩比2班好的是( )
淘气 笑笑 奇思
两个班男生人数一样多,1班男生只有1人不及格,而2班男生有2人不及格。 这次测试,1班男生的优秀率比2班男生的优秀率高。 这次测试,1班男生在及格、良好和优秀三个等级中的人数均比2班多。
A.只有淘气 B.只有笑笑
C.只有笑笑和奇思 D.只有淘气和笑笑
【考点】从统计图表中获取信息;扇形统计图.
【专题】统计数据的计算与应用;应用意识.
【答案】B
【分析】要体现“1班学生男生的成绩比2班好”,不能单独从不及格的人数方面进行比较,要从多方面对比,还可以从优秀率进行对比。据此解答。
【解答】解:淘气:仅从不及格的人数进行比较,不能反映“1班学生男生的成绩比2班好”;
笑笑:优秀率能反映“1班学生男生的成绩比2班好”;
奇思:1班男生在良好等级中的人数比2班少,所以说法错误;
综上,只有笑笑的观点能说明1班男生成绩比2班好。
故选:B。
【点评】本题主要考查了根据统计图表提供的信息解决实际问题的能力。
24.(2分)如图,下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,…,按此规律,则第(6)个图形中面积为1的正方形的个数为( )
A.20 B.27 C.35 D.40
【考点】数与形结合的规律.
【专题】探索数的规律.
【答案】B
【分析】第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的图象有2+3=5个,第(3)个图形中面积为1的正方形有2+3+4=9个,…,按此规律,第n个图形中面积为1的正方形有2+3+4+…+n,进一步求得第(6)个图形中面积为1的正方形的个数即可.
【解答】解:第(1)个图形中面积为1的正方形有2个,
第(2)个图形中面积为1的图象有2+3=5个,
第(3)个图形中面积为1的正方形有2+3+4=9个,
…,
按此规律,
第n个图形中面积为1的正方形有2+3+4+…+(n+1)个,
则第(6)个图形中面积为1的正方形的个数为2+3+4+5+6+7=27个.
故选:B.
【点评】此题考查图形的变化规律,找出图形与数字之间的运算规律,利用规律解决问题.
四.操作题(共4小题,满分10分)
25.(2分)按要求画出半径或直径,用字母表示并测量。
画出一条直径。
d= 2厘米
【考点】画圆.
【专题】作图题;应用意识.
【答案】(答案不唯一);2厘米。
【分析】利用直径的知识,量的直径是2厘米,由此解答本题即可。
【解答】解:(答案不唯一)d=2厘米
故答案为:2厘米。
【点评】本题考查的是圆的应用。
26.(2分)在圆中画出1条半径和1条直径,用字母标出圆心、半径、直径,再在这个圆中画出一个扇形。
【考点】扇形的认识;画圆.
【专题】数据分析观念.
【答案】
【分析】画出半径和直径,标出圆心O,半径r,直径d,将直径和半径所夹的扇形涂色标示即可。
【解答】解:
【点评】本题主要考查了圆的半径、直径和扇形的认识。
27.(4分)在如图中按要求画出指定的位置。
(1)医院在学校正西方向2000米处。
(2)图书馆在学校北偏东60°大约1500米处。
(3)菜市场在图书馆南偏东45°大约1000米处。
【考点】在平面图上标出物体的位置.
【专题】作图题;空间观念.
【答案】(1)(2)(3)。
【分析】依据图示可知,图上1厘米代表实际距离50000厘米,由此计算出医院与学校,图书馆与学校,菜市场与图书馆的图上距离,然后利用平面图上方向规定:上北下南左西右东,依据题意结合图示去解答。
【解答】解:图上1厘米代表实际距离50000厘米,即500米,
(1)2000÷500=4(厘米),如图:
(2)1500÷500=3(厘米),如图:
(3)1000÷500=2(厘米),如图:
【点评】本题考查的是根据方向和距离确定物体位置的应用。
28.(2分)手机作为现代化的通讯工具,给人们的生活带来了便利,为了更加合理的使用手机,实验小学社会实践调查小组以“你使用手机主要做什么”为主题,走进实验中学,对七年级学生进行了调查(每位同学只选择一项),并将结果分析整理,制成了下面两个统计图。其中:A.学习、B.通讯、C.娱乐、D.其他。
据以上信息请回答:
(1)本次调查共调查了 300 人,手机主要用来“通讯”的人占被调查人数的 20 %。
(2)手机主要用于“娱乐”的有 45 人。请将条形统计图补充完整。
(3)根据以上调查结果,你想对大家提出什么建议?
【考点】统计图表的填补;从统计图表中获取信息;扇形统计图.
【专题】综合题;数据分析观念.
【答案】(1)300,20;
(2)45,;
(3)大家合理使用手机,不要使用手机玩游戏等。(答案不唯一)
【分析】(1)调查人数=A类人数÷60%,手机主要用来“通讯”的人占被调查人数的百分之几=手机主要用来“通讯”的人÷被调查人数×100%,由此列式计算;
(2)手机主要用于“娱乐”的人数=总人数﹣180﹣60﹣15,由此解答本题;
(3)依据统计图去解答。(答案不唯一)
【解答】解:(1)180÷60%=300(人)
60÷300×100%=20%
答:本次调查共调查了300人,手机主要用来“通讯”的人占被调查人数的20%。
(2)300﹣180﹣60﹣15=45(人),如图:
;
(3)建议大家合理使用手机,不要使用手机玩游戏等。(答案不唯一)
故答案为:300,20;45。
【点评】本题考查的是统计图的应用。
五.解答题(共6小题,满分22分)
29.(3分)两块铁皮,第一块的面积比第二块小,从两块铁皮上各剪下它们的,共剪下36平方分米.原来这两块铁皮的面积各是多少?
【考点】分数四则复合应用题.
【专题】分数百分数应用题.
【答案】见试题解答内容
【分析】把第二块铁皮面积看作单位“1”,先求出第一块铁皮面积占的分率,再求出各剪下所占的分率,也就是36平方分米占第二块铁皮面积的分率,依据分数除法意义,求出第二块铁皮面积,最后依据分数乘法意义即可解答.
【解答】解:36÷[11×(1)],
=36÷[11],
=36÷[],
=36,
=60(平方分米),
60×(1),
=60,
=48(平方分米),
答:原来第一块铁皮面积是48平方分米,第二块铁皮面积是48平方分米.
【点评】分数除法意义是解答本题的依据,关键是求出36平方分米占第二块铁皮面积的分率.
30.(4分)水稻最早发源于中国,然后才传入世界各地。历史上有文字可查的水稻亩产量数据从春秋时代起,发展到汉朝,平均亩产量达63千克,比春秋时期水稻亩产量增产26%。至唐朝实行灌溉田后,平均亩产量达138千克。历经千年发展到清朝,亩产量是唐朝的200%。新中国成立后,1958年达400千克,1964年袁隆平开始杂交水稻的研究之后,至2019年水稻亩产量达1500千克。新中国成立后,短短四五十年的时间,袁隆平教授通过科学种田让粮食产量翻倍提升,解决了全世界的吃饭问题,让中国人彻底端平了饭碗。
(1)春秋时期水稻亩产量是多少千克?
(2)清朝水稻亩产量是多少千克?
(3)2019年比1958年水稻亩产量提升了百分之几?
(4)要描述各个时期水稻亩产量的多少,选用 条形 统计图比较合适;要描述各个时期水稻亩产量的变化情况选用 折线 统计图比较合适。
【考点】百分数的实际应用;统计图的选择.
【专题】计算题;分数和百分数;应用意识.
【答案】(1)50千克;
(2)276千克;
(3)275%;
(4)条形,折线。
【分析】(1)春秋时期水稻亩产量=汉朝平均亩产量÷(1+26%),依此列出算式计算即可求解;
(2)清朝水稻亩产量=唐朝平均亩产量×200%,依此列出算式计算即可求解;
(3)2019年比1958年水稻亩产量提升百分率=(2019年水稻亩产量﹣1958年水稻亩产量)÷1958年水稻亩产量×100%,依此列出算式计算即可求解;
(4)条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【解答】解:(1)63÷(1+26%)
=63÷1.26
=50(千克)
答:春秋时期水稻亩产量是50千克;
(2)138×200%=276(千克)
答:清朝水稻亩产量是276千克;
(3)(1500﹣400)÷400×100%
=1300÷400×100%
=275%
答:2019年比1958年水稻亩产量提升了275%;
(4)要描述各个时期水稻亩产量的多少,选用条形统计图比较合适;要描述各个时期水稻亩产量的变化情况选用折线统计图比较合适。
故答案为:条形,折线。
【点评】此题是考查百分数的实际应用;同时考查了根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
31.(4分)学校计划绿化一块287平方米的空地,先划出种树,剩下的按2:3种花和草。种花和草的面积各是多少平方米?
【考点】按比例分配应用题.
【专题】运算能力;应用意识.
【答案】82平方米,123平方米。
【分析】把这块地的面积看作单位“1”,先划出种树,用这块地的面积乘,求出种树的面积,再用这块地的面积﹣种树的面积,求出中花和草的面积,再根据按比例分配的计算方法,求出种花的面积和种草的面积。
【解答】解:(287﹣287)
=(287﹣82)
=205
=82(平方米)
(287﹣287)
=(287﹣82)
=205
=123(平方米)
答:种花的面积是82平方米,种草的面积是123平方米。
【点评】熟练掌握求一个数的几分之几的计算方法、按比例分配的计算方法是解答本题的关键。
32.(4分)只列式,不计算。
(1)某饲料加工厂5月份实际生产饲料5.5万吨,比计划多生产0.5万吨,比计划多生产百分之几?
(2)李阿姨把8000元钱存入银行,定期三年,年利率是2.35%。到期后李阿姨可得本息多少元?
(3)赵叔叔参加宿迁市半程马拉松比赛,小时跑千米。照这样的速度,他跑完21千米需要多少小时?
【考点】百分数的实际应用;简单的行程问题;存款利息与纳税相关问题.
【专题】应用意识.
【答案】(1)0.5÷(5.5﹣0.5);
(2)8000+8000×2.35%×3;
(3)21÷()。
【分析】(1)5月份实际生产饲料5.5万吨,比计划多生产0.5万吨,则计划生产(5.5﹣0.5)万吨。用0.5万吨除以(5.5﹣0.5)万吨。
(2)根据“利息=本金÷税率×存期”计算出利息,再加本金。
(3)先根据“速度=路程÷时间”求出赵叔叔的速度,再根据“时间=路程÷速度”即可解答。
【解答】解:(1)0.5÷(5.5﹣0.5)
=0.5÷5
=0.1
=10%
答:比计划多生产10%。
(2)8000+8000×2.35%×3
=8000+564
=8564(元)
答:到期后李阿姨可得本息8564元。
(3)21÷()
=21÷14
=1.5(小时)
答:他跑完21千米需要1.5小时。
【点评】(1)求一个数是另一个数的百分之几,用这个数除以另一个数;(2)关键记住计算公式;(3)关键掌握路程、时间、速度之间的关系。
33.(3分)求如图中阴影部分的周长和面积。(单位:分米)
【考点】组合图形的面积;圆与组合图形.
【专题】平面图形的认识与计算;几何直观.
【答案】周长是28.26分米,面积是10.26平方分米。
【分析】观察图形可得:阴影部分的周长=半径为6分米的圆的周长+直径为6分米的圆的周长,然后再根据圆的周长公式C=πd、C=2πr进行解答;
如图,通过旋转可得:阴影部分的面积=半径为6分米的圆的面积﹣底为6分米、高为6分米的三角形的面积,然后再根据圆的面积公式S=πr2,三角形的面积公式S=ah÷2进行解答。
【解答】解:3.14×6×2+3.14×6
=9.42+18.84
=28.26(分米)
3.14×626×6
=28.26﹣18
=10.26(平方分米)
答:阴影部分的周长是28.26分米,面积是10.26平方分米。
【点评】本题属于求组合图形周长或面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的周长或面积和还是求周长或面积差,然后根据周长公式或面积公式解答即可。
34.(4分)一块圆形铁皮和一块长方形铁皮的周长相等,已知长方形的长为9dm,宽为6.7dm,圆形铁皮的面积是多少?
【考点】有关圆的应用题.
【专题】平面图形的认识与计算;几何直观;应用意识.
【答案】78.5.
【分析】首先根据长方形的周长公式:C=(a+b)×2,求出长方形的周长,再根据圆的周长公式:C=2πr,那么r=C÷2π,据此求出半径,然后根据圆的面积公式:S=πr2,把数据代入公式解答.
【解答】解:(9+6.7)×2
=15.7×2
=31.4(分米)
3.14×(31.4÷3.14÷2)2
=3.14×52
=3.14×25
=78.5(平方分米)
答:圆形铁皮的面积是78.5平方分米.
【点评】此题主要考查长方形的周长公式、圆的周长公式、圆的面积公式的灵活运用,关键是熟记公式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
湖北省武汉市2025-2026学年六年级上学期期末模拟数学预测卷
一.计算题(共3小题,满分28分)
1.(10分)直接写出得数。
1﹣1%=
7÷0.1%= 0.23= 24 0.125= 1
2.(8分)计算下面各题,能简算的要简算。
3.(10分)解方程。
70%x=5.6
二.填空题(共11小题,满分20分)
4.(4分)70: %= (填小数)
5.(1分)红花的枝数比黄花的枝数多,则红花是黄花的 .
6.(2分)0.625的倒数是 ,的是 。
7.(1分)栽一种树苗,成活率为94%到100%,为保证470棵树能成活,需要至少栽树苗 棵。
8.(4分)在横线里填上“>”“<”或“=”。
①3.5÷0.9 3.5 ②4.6÷0.02 4.6÷0.2 ③4.6 4.6×1.2
④3.6÷1.2 3.6 ⑤3.2÷0.1 3.2×10 ⑥83×0.87 83
9.(1分)加工一批零件,甲单独做需要8天完成,乙单独做需要6天完成,两人合作, 天能完成。
10.(1分)一个三角形的三个内角度数的比是1:3:1,这个三角形按角分是 三角形,按边分是 三角形。
11.(2分)花生油的出油率是36%,现在要榨900千克花生油,要花生 千克。
12.(2分)老师用圆规在黑板上画圆,圆规两脚之间的距离是3分米。所画的圆的直径是 分米,周长是 分米,面积是 平方分米。
13.(1分)把一个圆按如图切开,拼成近似的长方形,近似的长方形的周长比圆的周长长6厘米,圆的面积是 cm2。
14.(1分)根据如表所示中数的排列规律,算一算A= ,B= 。
2 3
5 21
3 4
7 40
4 5
9 65
5 6
A B
三.选择题(共10小题,满分20分,每小题2分)
15.(2分)小红原来每天22:00睡觉,6:00 起床。国家实行“双减”政策后,小红现在每天21:20睡觉,7:20 起床。现在的睡眠时间比原来增加了( )%。
A.5% B.10% C.20% D.25%
16.(2分)有两根绳子。如果第一根剪去,那么还剩米;如果第二根剪去米,那么还剩总长的。原来两根绳子相比较,( )
A.第一根长 B.第二根长
C.两根一样长 D.无法确定哪根长
17.(2分)某商店出售两种服装,售价都是600元,一件是时令服装,可赚20%,另一件是过时服装,要赔20%,就这两件服装而言,商店的收入情况是( )
A.赚了 B.赔了 C.不赚不赔 D.无法确定
18.(2分)3:7的前项加上6,要使比值不变,后项应( )
A.加6 B.乘3 C.乘2
19.(2分)用12米长的铁条做直径是5分米的圆形铁环,最多可做( )个。
A.8 B.7
C.一个都做不了
20.(2分)有四个三角形,各自的三个内角的度数之比如下。其中( )对应的三角形一定不是直角三角形。
A.2:3:5 B.1:2:3 C.1:1:2 D.1:3:5
21.(2分)钟面上分针长5厘米,分针尖端在60分钟内所走过的路程是( )厘米。
A.31.4 B.50.24 C.12.56
22.(2分)甲、乙两个圆直径的比是2:1,那么它们面积的比是( )
A.2:1 B.4:1 C.8:1
23.(2分)“一分钟仰卧起坐”是《国家学生体质健康标准》的测试项目之一。红星小学六年级1班和2班所有男生均进行了此项测试,两个班的男生人数一样多。如图是六年级1班和2班男生“一分钟仰卧起坐”的测试成绩统计图。
根据如图信息,1班学生认为自己班男生的成绩比2班好,以下三位同学的观点能说明1班男生成绩比2班好的是( )
淘气 笑笑 奇思
两个班男生人数一样多,1班男生只有1人不及格,而2班男生有2人不及格。 这次测试,1班男生的优秀率比2班男生的优秀率高。 这次测试,1班男生在及格、良好和优秀三个等级中的人数均比2班多。
A.只有淘气 B.只有笑笑
C.只有笑笑和奇思 D.只有淘气和笑笑
24.(2分)如图,下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,…,按此规律,则第(6)个图形中面积为1的正方形的个数为( )
A.20 B.27 C.35 D.40
四.操作题(共4小题,满分10分)
25.(2分)按要求画出半径或直径,用字母表示并测量。
画出一条直径。
d=
26.(2分)在圆中画出1条半径和1条直径,用字母标出圆心、半径、直径,再在这个圆中画出一个扇形。
27.(4分)在如图中按要求画出指定的位置。
(1)医院在学校正西方向2000米处。
(2)图书馆在学校北偏东60°大约1500米处。
(3)菜市场在图书馆南偏东45°大约1000米处。
28.(2分)手机作为现代化的通讯工具,给人们的生活带来了便利,为了更加合理的使用手机,实验小学社会实践调查小组以“你使用手机主要做什么”为主题,走进实验中学,对七年级学生进行了调查(每位同学只选择一项),并将结果分析整理,制成了下面两个统计图。其中:A.学习、B.通讯、C.娱乐、D.其他。
据以上信息请回答:
(1)本次调查共调查了 人,手机主要用来“通讯”的人占被调查人数的 %。
(2)手机主要用于“娱乐”的有 人。请将条形统计图补充完整。
(3)根据以上调查结果,你想对大家提出什么建议?
五.解答题(共6小题,满分22分)
29.(3分)两块铁皮,第一块的面积比第二块小,从两块铁皮上各剪下它们的,共剪下36平方分米.原来这两块铁皮的面积各是多少?
30.(4分)水稻最早发源于中国,然后才传入世界各地。历史上有文字可查的水稻亩产量数据从春秋时代起,发展到汉朝,平均亩产量达63千克,比春秋时期水稻亩产量增产26%。至唐朝实行灌溉田后,平均亩产量达138千克。历经千年发展到清朝,亩产量是唐朝的200%。新中国成立后,1958年达400千克,1964年袁隆平开始杂交水稻的研究之后,至2019年水稻亩产量达1500千克。新中国成立后,短短四五十年的时间,袁隆平教授通过科学种田让粮食产量翻倍提升,解决了全世界的吃饭问题,让中国人彻底端平了饭碗。
(1)春秋时期水稻亩产量是多少千克?
(2)清朝水稻亩产量是多少千克?
(3)2019年比1958年水稻亩产量提升了百分之几?
(4)要描述各个时期水稻亩产量的多少,选用 统计图比较合适;要描述各个时期水稻亩产量的变化情况选用 统计图比较合适。
31.(4分)学校计划绿化一块287平方米的空地,先划出种树,剩下的按2:3种花和草。种花和草的面积各是多少平方米?
32.(4分)只列式,不计算。
(1)某饲料加工厂5月份实际生产饲料5.5万吨,比计划多生产0.5万吨,比计划多生产百分之几?
(2)李阿姨把8000元钱存入银行,定期三年,年利率是2.35%。到期后李阿姨可得本息多少元?
(3)赵叔叔参加宿迁市半程马拉松比赛,小时跑千米。照这样的速度,他跑完21千米需要多少小时?
33.(3分)求如图中阴影部分的周长和面积。(单位:分米)
34.(4分)一块圆形铁皮和一块长方形铁皮的周长相等,已知长方形的长为9dm,宽为6.7dm,圆形铁皮的面积是多少?
湖北省武汉市2025-2026学年六年级上学期期末模拟数学预测卷
参考答案与试题解析
一.计算题(共3小题,满分28分)
1.(10分)直接写出得数。
1﹣1%=
7÷0.1%= 0.23= 24 0.125= 1
【考点】分数的四则混合运算;分数乘法;分数除法.
【专题】运算能力.
【答案】见试题解答内容
【分析】根据小数、分数、百分数加减乘除法以及四则混合运算的顺序,直接进行口算即可。
【解答】解:
1﹣1%=0.99
7÷0.1%=7000 0.23=0.008 2415 0.125=2 1
【点评】本题考查了简单的计算,计算时要细心,注意平时积累经验,提高计算的水平。
2.(8分)计算下面各题,能简算的要简算。
【考点】分数的四则混合运算;运算定律与简便运算.
【专题】运算能力.
【答案】;;66。
【分析】按照乘法分配律计算;
先算小括号里面的乘法,再算除法;
按照乘法分配律计算。
【解答】解:
( )
9
(98+1)
99
=66
【点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
3.(10分)解方程。
70%x=5.6
【考点】百分数方程求解;分数方程求解.
【专题】运算能力.
【答案】x=8;x=60。
【分析】根据等式的基本性质,方程两边同时除以70%。
先计算出方程左边xxx,再根据等式的性质,方程两边同时除以。
【解答】解:70%x=5.6
70%x÷70%=5.6÷70%
x=8
xx=15
x=15
x15
x=60
【点评】解方程的依据是等式的性质。解答过程要注意书写格式:上、下行等号对齐;不能连等。
二.填空题(共11小题,满分20分)
4.(4分)70: 56 125 %= 1.25 (填小数)
【考点】比与分数、除法的关系;小数、分数和百分数之间的关系及其转化.
【专题】数感.
【答案】56,125,1.25。
【分析】根据比与分数的关系5:4,再根据比的性质比的前、后项都乘14就是70:56;根据分数与除法的关系5÷4=1.25;把1.25的小数点向右移动两位添上百分号就是125%。
【解答】解:70:56125%=1.25
故答案为:56,125,1.25。
【点评】此题主要是考查小数、分数、比、百分数之间的关系及转化。利用它们之间的关系和性质进行转化即可。
5.(1分)红花的枝数比黄花的枝数多,则红花是黄花的 .
【考点】分数的四则混合运算.
【专题】综合填空题;文字叙述题.
【答案】见试题解答内容
【分析】红花的枝数比黄花的枝数多,把黄花的数量看作单位“1”,红花对应的分率是1,要求红花是黄花的几分之几,用红花的数量除以黄花的数量即可.
【解答】解:(1)÷1
1
答:红花是黄花的.
故答案为:.
【点评】此题考查了判断单位“1”的方法:一般是把“比、占、是、相当于”后面的量看作单位“1”.
6.(2分)0.625的倒数是 ,的是 。
【考点】倒数的认识;分数乘法.
【专题】综合填空题;应用意识.
【答案】;。
【分析】若两个数的乘积是1,我们就称这两个数互为倒数。分数乘以分数:用分子相乘的积作为分子,用分母相乘的积作为分母。
【解答】解:0.625的倒数是;
1
故答案为:;。
【点评】本题考查的主要内容是倒数的应用和分数乘法计算问题。
7.(1分)栽一种树苗,成活率为94%到100%,为保证470棵树能成活,需要至少栽树苗 500 棵。
【考点】百分率应用题.
【专题】应用题;应用意识.
【答案】500。
【分析】因为成活率=成活树苗的棵数÷栽树苗的总棵数×100%,要保证470棵树能成活,成活率就要按照最低的94%来计算,所以要栽树苗的棵数=成活的棵数÷成活率,即470÷94%,由此列式计算得出答案。
【解答】解:470÷94%
=470÷0.94
=500(棵)
答:需要至少栽树苗500棵。
故答案为:500。
【点评】此题的关键是根据“要栽树苗的棵数、成活的棵数、成活率”三者间的关系,求出要栽树苗的棵数。
8.(4分)在横线里填上“>”“<”或“=”。
①3.5÷0.9 > 3.5 ②4.6÷0.02 > 4.6÷0.2 ③4.6 < 4.6×1.2
④3.6÷1.2 < 3.6 ⑤3.2÷0.1 = 3.2×10 ⑥83×0.87 < 83
【考点】商的变化规律;积的变化规律.
【专题】综合判断题;运算能力.
【答案】>;>;<;<;=;<。
【分析】①一个数(0除外)除以小于1的数(0除外),商大于这个数,据此判断;
②计算后比较大小;
③一个数(0除外)乘大于1的数,积大于这个数,据此判断;
④一个数(0除外)除以大于1的数,商小于这个数,据此判断;
⑤除以一个数,等于乘这个数的倒数,据此判断;
⑥一个数(0除外)乘小于1的数,积小于这个数,据此判断。
【解答】解:①3.5÷0.9>3.5
②因为4.6÷0.02=230,4.6÷0.2=23,所以4.6÷0.02>4.6÷0.2
③4.6<4.6×1.2
④3.6÷1.2<3.6
⑤3.2÷0.1=3.2×10
⑥83×0.87<83
故答案为:>;>;<;<;=;<。
【点评】本题考查了积的变化规律和商的变化规律的应用。
9.(1分)加工一批零件,甲单独做需要8天完成,乙单独做需要6天完成,两人合作, 3 天能完成。
【考点】简单的工程问题.
【专题】应用题;应用意识.
【答案】3。
【分析】首先根据工作效率=工作量÷工作时间,把这批零件的工作量看成单位“1”,甲的工作效率是,乙的工作效率是,用工作总量除以合作的工作效率之和即可解答此题。
【解答】解:1÷()
=1
=3(天)
答:3天能完成。
故答案为:3。
【点评】此题考查儿了简单的工程问题。
10.(1分)一个三角形的三个内角度数的比是1:3:1,这个三角形按角分是 钝角 三角形,按边分是 等腰 三角形。
【考点】按比例分配应用题.
【专题】比和比例应用题;几何直观;运算能力;应用意识.
【答案】钝角,等腰。
【分析】根据三角形内角和定理,三角形三个内角之和是180°,这个三角形最大角占三个角度数的,根据分数乘法的意义,用180°乘就是这个三角形中最大角的度数。这个最大角如果是锐角,这个三角形就是锐角三角形;如果是直角,这个三角形就是直角三角形;如果是钝角,这个三角形就是钝角三角形。在三角形中相等的角所对的边相等,这个三角形中有两个角相等,就有两条边相等,根据等腰三角形的意义,此三角形是等腰三角形。
【解答】解:180°
=180°
=108°
这个三角形按角分是钝角三角形。
因为个三角形的三个内角度数的比是1:3:1
所以这个三角形中有两条边相等,按边分,这个三角形是等腰三角形
答:这个三角形按角分是钝角三角形,按边分是等腰三角形。
故答案为:钝角,等腰。
【点评】此题考查的知识点有:三角形内角和定理、按比例分配问题、三角形的分类等。
11.(2分)花生油的出油率是36%,现在要榨900千克花生油,要花生 2500 千克。
【考点】百分率应用题.
【专题】应用意识.
【答案】2500。
【分析】首先理解“出油率”的概念,出油率是指出油的重量占作物重量的百分比,即出油率100%,已知出油率是36%,现在要榨900千克花生油,求需要花生多少千克,用油的重量÷出油率,即900÷36%,计算即可。
【解答】解:900÷36%
=900÷0.36
=2500(千克)
答:要花生2500千克。
故答案为:2500。
【点评】此题考查了成活率的概念,熟练掌握是关键。
12.(2分)老师用圆规在黑板上画圆,圆规两脚之间的距离是3分米。所画的圆的直径是 6 分米,周长是 18.84 分米,面积是 28.26 平方分米。
【考点】圆、圆环的面积;圆、圆环的周长.
【专题】应用意识.
【答案】6,18.84,28.26。
【分析】根据直径与半径的关系,d=2r,圆的周长公式:C=2πr,圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:3×2=6(分米)
2×3.14×3=18.84(分米)
3.14×32
=3.14×9
=28.26(平方分米)
答:所画圆的直径是6分米,周长是18.84分米,面积是28.26平方分米。
故答案为:6,18.84,28.26。
【点评】此题主要考查圆的周长公式、圆的面积公式的灵活运用,关键是熟记公式。
13.(1分)把一个圆按如图切开,拼成近似的长方形,近似的长方形的周长比圆的周长长6厘米,圆的面积是 28.26 cm2。
【考点】圆与组合图形;圆、圆环的面积.
【专题】平面图形的认识与计算;空间观念.
【答案】28.26。
【分析】根据圆面积公式的推导过程可知,把一个圆剪拼成一个近似长方形,这个长方形的长等于圆周长的一半,长方形的宽等于圆的半径,拼成的长方形的周长比圆的周长增加了两条比较的长度,据此可以求出半径,根据圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:6÷2=3(厘米)
3.14×32
=3.14×9
=28.26(平方厘米)
答:圆的面积是28.26平方厘米。
故答案为:28.26。
【点评】此题考查的目的是理解掌握圆面积公式的推导过程及应用,圆的周长和圆的面积公式及应用。
14.(1分)根据如表所示中数的排列规律,算一算A= 11 ,B= 96 。
2 3
5 21
3 4
7 40
4 5
9 65
5 6
A B
【考点】数表中的规律.
【专题】压轴题;运算能力.
【答案】11,96。
【分析】规律:左下角的数依次加2,第一列的数字和乘右上角的数等于右下角的数。
【解答】解:A=9+2=11
B=(5+11)×6=96
故答案为:11,96。
【点评】本题考查了数表中的规律,关键是找到规律。
三.选择题(共10小题,满分20分,每小题2分)
15.(2分)小红原来每天22:00睡觉,6:00 起床。国家实行“双减”政策后,小红现在每天21:20睡觉,7:20 起床。现在的睡眠时间比原来增加了( )%。
A.5% B.10% C.20% D.25%
【考点】百分数的实际应用.
【专题】应用意识.
【答案】D
【分析】先用24时减去22时的差加上6时,求出小红原来的睡眠时间;再用24时减去21时20分的差加上7时20分,求出小红实行“双减”政策后的睡眠时间,最后求出现在的睡眠时间比原来增加了百分之几即可。
【解答】解:24时﹣22时+6时=8小时
24时﹣21时20分+7时20分=10小时
(10﹣8)÷8
=2÷8
=0.25
=25%
答:现在的睡眠时间比原来增加了25%。
故选:D。
【点评】解答本题需熟练掌握经历的时间的计算方法,明确求一个数比另一个数多百分之几的计算方法。
16.(2分)有两根绳子。如果第一根剪去,那么还剩米;如果第二根剪去米,那么还剩总长的。原来两根绳子相比较,( )
A.第一根长 B.第二根长
C.两根一样长 D.无法确定哪根长
【考点】分数除法应用题.
【专题】综合题;应用意识.
【答案】A
【分析】第一根绳子剪去,剩下的占第一根绳子长度的,还剩米。第二根绳子剪去米后,还剩总长的,则剪去的占第二根绳子长度的。根据已知比较量求单位“1”用除法计算,用比较量除以分率即可分别求出两根绳子原来的长度。最后进行比较即可。据此解答。
【解答】解:第一根绳子的长度:
=2(米)
第二根绳子的长度:
(米)
2,所以原来第一根绳子长。
故选:A。
【点评】已知一个数的几分之几是多少求这个数用除法计算。
17.(2分)某商店出售两种服装,售价都是600元,一件是时令服装,可赚20%,另一件是过时服装,要赔20%,就这两件服装而言,商店的收入情况是( )
A.赚了 B.赔了 C.不赚不赔 D.无法确定
【考点】百分数的实际应用.
【专题】应用意识.
【答案】B
【分析】把时令服装的进价看作单位“1”,则售价=进价×(1+20%);把过时服装的进价看作单位“1”,则售价=进价×(1﹣20%),求出两件服装的进价和与售价和进行比较即可。
【解答】解:600÷(1+20%)+600÷(1﹣20%)
=500+750
=1250(元)
600×2=1200(元)
1250>1200
答:就这两件服装而言,商店的收入情况是赔了。
故选:B。
【点评】本题主要考查百分数的实际应用,关键是利用进价与售价的数量关系做题。
18.(2分)3:7的前项加上6,要使比值不变,后项应( )
A.加6 B.乘3 C.乘2
【考点】比的性质.
【专题】推理能力.
【答案】B
【分析】3:7的前项加上6,即3+6=9,由3到9,扩大到原来的9÷3=3倍,要使比值不变,后项应扩大到原来的3倍,据此解答即可。
【解答】解:3+6=9
9÷3=3
所以把3:7的前项加上6,要使比值不变,后项应乘3。
故选:B。
【点评】此题考查比的性质的运用,比的前项和后项同时乘或除以相同的数(0除外),比值才不变。
19.(2分)用12米长的铁条做直径是5分米的圆形铁环,最多可做( )个。
A.8 B.7
C.一个都做不了
【考点】圆、圆环的周长.
【专题】几何直观.
【答案】B
【分析】先把单位进行换算,即12米=120分米,圆形铁环的周长=直径×π,然后用铁条的长度除以铁环的周长,把结果取整即可。
【解答】解:12米=120分米
5×3.14=15.7(分米)
120÷15.7≈7(个)
答:最多可以做7个。
故选:B。
【点评】此题主要考查圆的周长在实际生活中的应用。关键是知道用铁条的长度除以一个铁环的周长就是做的个数,结果要用去尾法取近似值。
20.(2分)有四个三角形,各自的三个内角的度数之比如下。其中( )对应的三角形一定不是直角三角形。
A.2:3:5 B.1:2:3 C.1:1:2 D.1:3:5
【考点】比的应用.
【专题】推理能力;应用意识.
【答案】D
【分析】根据直角三角形两个锐角的和等于直角,据此解答即可。
【解答】解:A.2+3=5,所以三角形三个内角度数之比为2:3:5的三角形是直角三角形。
B.1+2=3,所以三角形三个内角度数之比为1:2:3的三角形是直角三角形。
C.1+1=2,所以三角形三个内角度数之比为1:1:2的三角形是直角三角形。
D.1+3≠5,所以三角形三个内角度数之比为1:3:5的三角形不是直角三角形。
故选:D。
【点评】熟练掌握直角三角形的性质,是解答此题的关键。
21.(2分)钟面上分针长5厘米,分针尖端在60分钟内所走过的路程是( )厘米。
A.31.4 B.50.24 C.12.56
【考点】圆、圆环的周长.
【专题】应用意识.
【答案】A
【分析】60分钟分针针尖走过的路程是一个半径为5厘米圆的周长,根据圆周长的周长公式“C=2πr”,列式即可解答。
【解答】解:2×3.14×5
=6.28×5
=31.4(cm)
所以钟面上分针长5厘米,分针尖端在60分钟内所走过的路程是31.4厘米。
故选:A。
【点评】关键是掌握并灵活运用圆的周长公式。
22.(2分)甲、乙两个圆直径的比是2:1,那么它们面积的比是( )
A.2:1 B.4:1 C.8:1
【考点】圆、圆环的面积;比的应用.
【专题】应用意识.
【答案】B
【分析】根据直径与半径的关系,d=2r,甲、乙两个圆直径的比是2:1,则甲、乙两个圆半径的比是2:1,再根据圆的面积公式:S=πr2,因为圆周率是一定的,所以甲、乙两个圆面积的比等于半径平方的比。据此解答即可。
【解答】解:22:12=4:1
答:它们面积的比是4:1。
故选:B。
【点评】此题主要考查圆的面积公式的灵活运用,因数与积的变化规律及应用,比的意义及应用。
23.(2分)“一分钟仰卧起坐”是《国家学生体质健康标准》的测试项目之一。红星小学六年级1班和2班所有男生均进行了此项测试,两个班的男生人数一样多。如图是六年级1班和2班男生“一分钟仰卧起坐”的测试成绩统计图。
根据如图信息,1班学生认为自己班男生的成绩比2班好,以下三位同学的观点能说明1班男生成绩比2班好的是( )
淘气 笑笑 奇思
两个班男生人数一样多,1班男生只有1人不及格,而2班男生有2人不及格。 这次测试,1班男生的优秀率比2班男生的优秀率高。 这次测试,1班男生在及格、良好和优秀三个等级中的人数均比2班多。
A.只有淘气 B.只有笑笑
C.只有笑笑和奇思 D.只有淘气和笑笑
【考点】从统计图表中获取信息;扇形统计图.
【专题】统计数据的计算与应用;应用意识.
【答案】B
【分析】要体现“1班学生男生的成绩比2班好”,不能单独从不及格的人数方面进行比较,要从多方面对比,还可以从优秀率进行对比。据此解答。
【解答】解:淘气:仅从不及格的人数进行比较,不能反映“1班学生男生的成绩比2班好”;
笑笑:优秀率能反映“1班学生男生的成绩比2班好”;
奇思:1班男生在良好等级中的人数比2班少,所以说法错误;
综上,只有笑笑的观点能说明1班男生成绩比2班好。
故选:B。
【点评】本题主要考查了根据统计图表提供的信息解决实际问题的能力。
24.(2分)如图,下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,…,按此规律,则第(6)个图形中面积为1的正方形的个数为( )
A.20 B.27 C.35 D.40
【考点】数与形结合的规律.
【专题】探索数的规律.
【答案】B
【分析】第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的图象有2+3=5个,第(3)个图形中面积为1的正方形有2+3+4=9个,…,按此规律,第n个图形中面积为1的正方形有2+3+4+…+n,进一步求得第(6)个图形中面积为1的正方形的个数即可.
【解答】解:第(1)个图形中面积为1的正方形有2个,
第(2)个图形中面积为1的图象有2+3=5个,
第(3)个图形中面积为1的正方形有2+3+4=9个,
…,
按此规律,
第n个图形中面积为1的正方形有2+3+4+…+(n+1)个,
则第(6)个图形中面积为1的正方形的个数为2+3+4+5+6+7=27个.
故选:B.
【点评】此题考查图形的变化规律,找出图形与数字之间的运算规律,利用规律解决问题.
四.操作题(共4小题,满分10分)
25.(2分)按要求画出半径或直径,用字母表示并测量。
画出一条直径。
d= 2厘米
【考点】画圆.
【专题】作图题;应用意识.
【答案】(答案不唯一);2厘米。
【分析】利用直径的知识,量的直径是2厘米,由此解答本题即可。
【解答】解:(答案不唯一)d=2厘米
故答案为:2厘米。
【点评】本题考查的是圆的应用。
26.(2分)在圆中画出1条半径和1条直径,用字母标出圆心、半径、直径,再在这个圆中画出一个扇形。
【考点】扇形的认识;画圆.
【专题】数据分析观念.
【答案】
【分析】画出半径和直径,标出圆心O,半径r,直径d,将直径和半径所夹的扇形涂色标示即可。
【解答】解:
【点评】本题主要考查了圆的半径、直径和扇形的认识。
27.(4分)在如图中按要求画出指定的位置。
(1)医院在学校正西方向2000米处。
(2)图书馆在学校北偏东60°大约1500米处。
(3)菜市场在图书馆南偏东45°大约1000米处。
【考点】在平面图上标出物体的位置.
【专题】作图题;空间观念.
【答案】(1)(2)(3)。
【分析】依据图示可知,图上1厘米代表实际距离50000厘米,由此计算出医院与学校,图书馆与学校,菜市场与图书馆的图上距离,然后利用平面图上方向规定:上北下南左西右东,依据题意结合图示去解答。
【解答】解:图上1厘米代表实际距离50000厘米,即500米,
(1)2000÷500=4(厘米),如图:
(2)1500÷500=3(厘米),如图:
(3)1000÷500=2(厘米),如图:
【点评】本题考查的是根据方向和距离确定物体位置的应用。
28.(2分)手机作为现代化的通讯工具,给人们的生活带来了便利,为了更加合理的使用手机,实验小学社会实践调查小组以“你使用手机主要做什么”为主题,走进实验中学,对七年级学生进行了调查(每位同学只选择一项),并将结果分析整理,制成了下面两个统计图。其中:A.学习、B.通讯、C.娱乐、D.其他。
据以上信息请回答:
(1)本次调查共调查了 300 人,手机主要用来“通讯”的人占被调查人数的 20 %。
(2)手机主要用于“娱乐”的有 45 人。请将条形统计图补充完整。
(3)根据以上调查结果,你想对大家提出什么建议?
【考点】统计图表的填补;从统计图表中获取信息;扇形统计图.
【专题】综合题;数据分析观念.
【答案】(1)300,20;
(2)45,;
(3)大家合理使用手机,不要使用手机玩游戏等。(答案不唯一)
【分析】(1)调查人数=A类人数÷60%,手机主要用来“通讯”的人占被调查人数的百分之几=手机主要用来“通讯”的人÷被调查人数×100%,由此列式计算;
(2)手机主要用于“娱乐”的人数=总人数﹣180﹣60﹣15,由此解答本题;
(3)依据统计图去解答。(答案不唯一)
【解答】解:(1)180÷60%=300(人)
60÷300×100%=20%
答:本次调查共调查了300人,手机主要用来“通讯”的人占被调查人数的20%。
(2)300﹣180﹣60﹣15=45(人),如图:
;
(3)建议大家合理使用手机,不要使用手机玩游戏等。(答案不唯一)
故答案为:300,20;45。
【点评】本题考查的是统计图的应用。
五.解答题(共6小题,满分22分)
29.(3分)两块铁皮,第一块的面积比第二块小,从两块铁皮上各剪下它们的,共剪下36平方分米.原来这两块铁皮的面积各是多少?
【考点】分数四则复合应用题.
【专题】分数百分数应用题.
【答案】见试题解答内容
【分析】把第二块铁皮面积看作单位“1”,先求出第一块铁皮面积占的分率,再求出各剪下所占的分率,也就是36平方分米占第二块铁皮面积的分率,依据分数除法意义,求出第二块铁皮面积,最后依据分数乘法意义即可解答.
【解答】解:36÷[11×(1)],
=36÷[11],
=36÷[],
=36,
=60(平方分米),
60×(1),
=60,
=48(平方分米),
答:原来第一块铁皮面积是48平方分米,第二块铁皮面积是48平方分米.
【点评】分数除法意义是解答本题的依据,关键是求出36平方分米占第二块铁皮面积的分率.
30.(4分)水稻最早发源于中国,然后才传入世界各地。历史上有文字可查的水稻亩产量数据从春秋时代起,发展到汉朝,平均亩产量达63千克,比春秋时期水稻亩产量增产26%。至唐朝实行灌溉田后,平均亩产量达138千克。历经千年发展到清朝,亩产量是唐朝的200%。新中国成立后,1958年达400千克,1964年袁隆平开始杂交水稻的研究之后,至2019年水稻亩产量达1500千克。新中国成立后,短短四五十年的时间,袁隆平教授通过科学种田让粮食产量翻倍提升,解决了全世界的吃饭问题,让中国人彻底端平了饭碗。
(1)春秋时期水稻亩产量是多少千克?
(2)清朝水稻亩产量是多少千克?
(3)2019年比1958年水稻亩产量提升了百分之几?
(4)要描述各个时期水稻亩产量的多少,选用 条形 统计图比较合适;要描述各个时期水稻亩产量的变化情况选用 折线 统计图比较合适。
【考点】百分数的实际应用;统计图的选择.
【专题】计算题;分数和百分数;应用意识.
【答案】(1)50千克;
(2)276千克;
(3)275%;
(4)条形,折线。
【分析】(1)春秋时期水稻亩产量=汉朝平均亩产量÷(1+26%),依此列出算式计算即可求解;
(2)清朝水稻亩产量=唐朝平均亩产量×200%,依此列出算式计算即可求解;
(3)2019年比1958年水稻亩产量提升百分率=(2019年水稻亩产量﹣1958年水稻亩产量)÷1958年水稻亩产量×100%,依此列出算式计算即可求解;
(4)条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【解答】解:(1)63÷(1+26%)
=63÷1.26
=50(千克)
答:春秋时期水稻亩产量是50千克;
(2)138×200%=276(千克)
答:清朝水稻亩产量是276千克;
(3)(1500﹣400)÷400×100%
=1300÷400×100%
=275%
答:2019年比1958年水稻亩产量提升了275%;
(4)要描述各个时期水稻亩产量的多少,选用条形统计图比较合适;要描述各个时期水稻亩产量的变化情况选用折线统计图比较合适。
故答案为:条形,折线。
【点评】此题是考查百分数的实际应用;同时考查了根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
31.(4分)学校计划绿化一块287平方米的空地,先划出种树,剩下的按2:3种花和草。种花和草的面积各是多少平方米?
【考点】按比例分配应用题.
【专题】运算能力;应用意识.
【答案】82平方米,123平方米。
【分析】把这块地的面积看作单位“1”,先划出种树,用这块地的面积乘,求出种树的面积,再用这块地的面积﹣种树的面积,求出中花和草的面积,再根据按比例分配的计算方法,求出种花的面积和种草的面积。
【解答】解:(287﹣287)
=(287﹣82)
=205
=82(平方米)
(287﹣287)
=(287﹣82)
=205
=123(平方米)
答:种花的面积是82平方米,种草的面积是123平方米。
【点评】熟练掌握求一个数的几分之几的计算方法、按比例分配的计算方法是解答本题的关键。
32.(4分)只列式,不计算。
(1)某饲料加工厂5月份实际生产饲料5.5万吨,比计划多生产0.5万吨,比计划多生产百分之几?
(2)李阿姨把8000元钱存入银行,定期三年,年利率是2.35%。到期后李阿姨可得本息多少元?
(3)赵叔叔参加宿迁市半程马拉松比赛,小时跑千米。照这样的速度,他跑完21千米需要多少小时?
【考点】百分数的实际应用;简单的行程问题;存款利息与纳税相关问题.
【专题】应用意识.
【答案】(1)0.5÷(5.5﹣0.5);
(2)8000+8000×2.35%×3;
(3)21÷()。
【分析】(1)5月份实际生产饲料5.5万吨,比计划多生产0.5万吨,则计划生产(5.5﹣0.5)万吨。用0.5万吨除以(5.5﹣0.5)万吨。
(2)根据“利息=本金÷税率×存期”计算出利息,再加本金。
(3)先根据“速度=路程÷时间”求出赵叔叔的速度,再根据“时间=路程÷速度”即可解答。
【解答】解:(1)0.5÷(5.5﹣0.5)
=0.5÷5
=0.1
=10%
答:比计划多生产10%。
(2)8000+8000×2.35%×3
=8000+564
=8564(元)
答:到期后李阿姨可得本息8564元。
(3)21÷()
=21÷14
=1.5(小时)
答:他跑完21千米需要1.5小时。
【点评】(1)求一个数是另一个数的百分之几,用这个数除以另一个数;(2)关键记住计算公式;(3)关键掌握路程、时间、速度之间的关系。
33.(3分)求如图中阴影部分的周长和面积。(单位:分米)
【考点】组合图形的面积;圆与组合图形.
【专题】平面图形的认识与计算;几何直观.
【答案】周长是28.26分米,面积是10.26平方分米。
【分析】观察图形可得:阴影部分的周长=半径为6分米的圆的周长+直径为6分米的圆的周长,然后再根据圆的周长公式C=πd、C=2πr进行解答;
如图,通过旋转可得:阴影部分的面积=半径为6分米的圆的面积﹣底为6分米、高为6分米的三角形的面积,然后再根据圆的面积公式S=πr2,三角形的面积公式S=ah÷2进行解答。
【解答】解:3.14×6×2+3.14×6
=9.42+18.84
=28.26(分米)
3.14×626×6
=28.26﹣18
=10.26(平方分米)
答:阴影部分的周长是28.26分米,面积是10.26平方分米。
【点评】本题属于求组合图形周长或面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的周长或面积和还是求周长或面积差,然后根据周长公式或面积公式解答即可。
34.(4分)一块圆形铁皮和一块长方形铁皮的周长相等,已知长方形的长为9dm,宽为6.7dm,圆形铁皮的面积是多少?
【考点】有关圆的应用题.
【专题】平面图形的认识与计算;几何直观;应用意识.
【答案】78.5.
【分析】首先根据长方形的周长公式:C=(a+b)×2,求出长方形的周长,再根据圆的周长公式:C=2πr,那么r=C÷2π,据此求出半径,然后根据圆的面积公式:S=πr2,把数据代入公式解答.
【解答】解:(9+6.7)×2
=15.7×2
=31.4(分米)
3.14×(31.4÷3.14÷2)2
=3.14×52
=3.14×25
=78.5(平方分米)
答:圆形铁皮的面积是78.5平方分米.
【点评】此题主要考查长方形的周长公式、圆的周长公式、圆的面积公式的灵活运用,关键是熟记公式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
