2026年中考《数学》复习课件 专题七 图形与变换-第31讲 图形的平移、对称、旋转与位似 (共67张PPT)

(共67张PPT)
复习讲义
第一篇 考点精讲
专题七 图形与变换
第31讲 图形的平移、对称、旋转与位似
聚焦核心
1.图形的平移
定义 把一个图形沿着某一个方向移动一定的______
两要素 平移的______和平移的______
性质 平移前后，图形的______和______完全相同
连接各组对应点的线段______（或共线）且______
距离
方向
距离
形状
大小
平行
相等
2.轴对称和轴对称图形
种 类 轴对称 轴对称图形
定 义 把一个图形沿着某一条直线折 叠，若它能够与另一个图形 ______，则这两个图形关于这条 直线成________，这条直线叫作 ________ 如果一个平面图形沿着一条直
线折叠，直线两旁的部分能互
相______，这个图形叫作轴对
称图形，这条直线就是它的
________
重合
轴对称
对称轴
重合
对称轴
性 质 如果两个图形关于某条直线对 称，那么对称轴是对应点所连线 段的____________ 轴对称图形的对称轴是任意一
对对应点所连线段的_________
___
关于某条直线对称的两个图形是 全等的 轴对称图形的对应线段
______，对应角也______
续表
垂直平分线
垂直平分线
相等
相等
3.中心对称和中心对称图形
种 类 中心对称 中心对称图形
定 义 把一个图形绕着某一点旋转 _____ ，如果它能与另一个 图形______，就说这两个图 形关于这个点对称或中心对 称，这个点叫作__________ 把一个图形绕着某一点旋转____ ，如果旋转后的图形能够与原来的
图形______，那么这个图形叫作中心
对称图形，这个点就是它的对称中心
___
180
重合
对称中心
180
重合
性 质 中心对称的两个图形，对称 点所连的线段都经过_______ ___，并且被对称中心______ 中心对称图形上所有点关于对称中心
的对称点都仍在这个图形上，且每一
对对称点所连的线段都被__________
平分
中心对称的两个图形是全等 图形 任何一条经过_________的直线都将这个中心对称图形分成两个全等的图形
续表
对称中心
平分
对称中心
对称中心
4.图形的旋转
定义 把一个图形绕着平面内某一点转动一个______，叫作图形的
旋转，这一点叫作__________，转动的角叫作________
三要素 旋转______、旋转______和旋转____
性质 旋转前后，图形的______和______完全相同
对应点到旋转中心的距离______
对应点与旋转中心所连线段的夹角等于________
角度
旋转中心
旋转角
中心
方向
角
形状
大小
相等
旋转角
5.图形的位似
定 义 如果两个图形不仅相似，而且对应点的连线相交于______，那么
这两个图形叫作位似图形，这个点叫作__________
性 质 位似图形上任意一对对应点到位似中心的距离之比都等于
________
在平面直角坐标系中，如果以原点为位似中心，画出一个与原图
形位似的图形，使其与原图形的相似比为 ，那么与原图形上的点
对应的位似图形上的点的坐标为________或___________
一点
位似中心
相似比
第31讲 图形的平移、对称、旋转与位似
案例分析
考点一 平移及其性质
名师指导
有关图形的平移问题，要注意平移的方向与距离，并注意对应点的
确定.解题时，要充分利用平移的性质，得到平行的线段、相等的线段
和相等的角，为解决问题提供条件.
图1
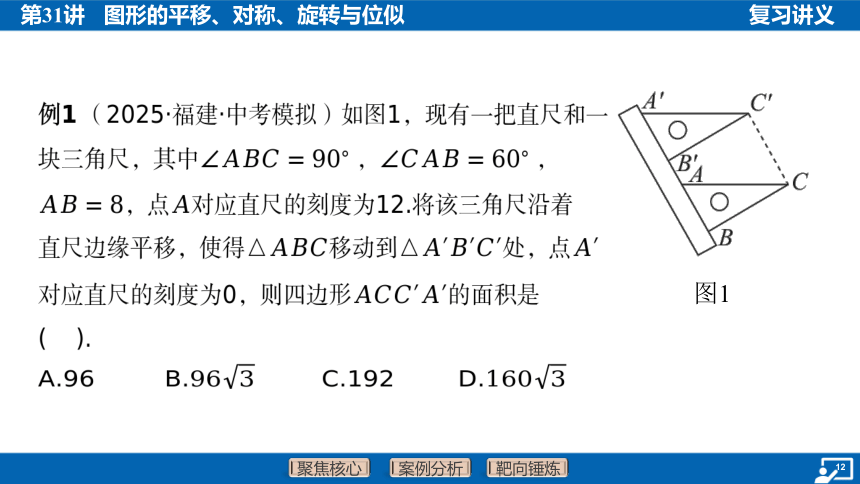
例1 （2025·福建·中考模拟）如图1，现有一把直尺和一
块三角尺，其中 ， ，
，点 对应直尺的刻度为12.将该三角尺沿着
直尺边缘平移，使得移动到处，点
对应直尺的刻度为0，则四边形 的面积是
( ).
A.96 B. C.192 D.
图1
提示：在中， ，， ，则 .由平移的性质，可知，，所以四边形 为平行四边形.因为点A对应直尺的刻度为12，点 对应直尺的刻度为0，所以 .所以 ．
思路点拨 由平移的性质，可知四边形 是平行四边形.根据题意，只
要求出，的长，就可求的面积. 的长可利用锐角三角函
数求得，的长可利用点， 对应直尺的刻度求得，从而问题可解.
【答案】B
图2
1.（2025·广西河池·模拟）水是生命之源，滋润着世间万
物.如图2，国家节水标志由水滴、手掌和地球构成，其寓
意是像对待掌上明珠一样，珍惜每一滴水！下列图形可以
通过平移节水标志得到的是( ).
C
A. B. C. D.
考点专练
2.（2024·山东东营·中考）如图3，将沿方向平移 得到
，若的周长为，则四边形的周长为____ .
30
图3
考点二 对称及其性质
名师指导
对于折叠问题，要注意折叠前后对应线段相等、对应角相等.关于
矩形、正方形的折叠问题，通常利用矩形、正方形以及折叠的性质，得
到等边、等角，为判定全等（或相似）三角形提供条件；由矩形的四个
角为直角，得到直角三角形，从而可根据勾股定理求解.
图4
例2 （2024·江苏常州·中考）如图4，在
中， ，，，是边 的
中点，是边上一点，连接，.将 沿
翻折，点落在上的点处，则 __.
图4
思路点拨 根据已知条件无法直接运用勾股定理计算
出的长，因此考虑将求 的长转化为求其他线段
的长.由折叠的性质，得， ，
.因此求出 的长，即可得到
的长.在中，设 ，运用勾股定理列
方程求解.
图4
提示：因为，，， 是边
的中点，所以 .由勾股定理，得
.由折叠的性质，得
，， .所
以， .设 ，则
.在 中，由勾股定理，得
.解得. 故 ．
考点专练
3.（2024·湖北武汉·中考）现实世界中，对称现象无处不在，我国的方
块字中有些也具有对称性．下列汉字属于轴对称图形的是( ).
C
A. B.
C. D.
图5
4.如图5，有一矩形纸片 ，
， .将纸片折叠，使
落在边上，折痕为 ，再将
以为折痕向右折叠， 与
交于点， 的值是__.
提示：经过两次折叠后，， .由
，得.所以 .
考点三 旋转及其性质
名师指导
1.有关图形旋转的问题,一般转化为关键点的旋转问题求解.解题时，
要充分利用旋转的性质，即旋转前后的图形全等， 对应点到旋转中心
的距离相等，对应点与旋转中心所连线段的夹角等于旋转角.
2.有关平面直角坐标系内点的旋转问题的解决方法：通常分别过已
知点和所求点作轴、轴的垂线，根据已知点的坐标得到对应线段的长，
然后利用旋转的性质求解.
例3 一题多问 如图6，绕某一点逆时针旋转 后得
到，其中点，的对应点分别是点，，点落在边 上，延
长交于点，，相交于点， .
图6
（1）旋转中心为_____，旋转角的度数为____.
（2） 是__________三角形.
点
等腰直角
思路点拨（1）旋转前后位置没有发生变化的点，即和的公共点即为旋转中心， 的度数即为旋转角的度数.
思路点拨 （2）由旋转的性质可得对应边相等，即 ，且 的度数等于旋转角的度数，由此可判断 的形状.
（3）判断与 的位置关系，并说明理由.
图6
解：.
理由如下：由旋转的性质，得
， .
.
∴ .
.
思路点拨 （3）观察图形发现，与 相交，则可猜想它们互相垂直，结合旋转的性质，求出 的度数即可得出结论.
图6
（4）求证： .
证明：由旋转的性质，得， ， .
.
在和中，， ，，
思路点拨（4）结合（2）的结论，易得，又 .则证明即可证得.观察图形，发现， 分别在和 中，证这两个三角形全等即可.
图6
.
由（2）知是等腰直角三角形， ，即 .
5.传统文化（2024·四川内江·中考）2024年6月5日，是二十四节气的芒
种.二十四节气是我国劳动人民独创的文化遗产，能反映季节的变化，
指导农事活动.下列四幅图片分别代表“芒种”“白露”“立夏”“大雪”，其中
属于中心对称图形的是( ).
D
A. B.
C. D.
考点专练
6.（2024·山东滨州·中考）一副三角尺按图7所示的方式摆放，把三角尺
绕公共顶点顺时针旋转至图8所示的位置，当时，
____ .
75
图7
图8
考点四 位似及其性质
名师指导
在平面直角坐标系中，可以用位似图形上对应点的坐标之间的关系
来表示它们的位似关系.一般地，如果以原点为位似中心，新图形与原
图形的相似比为，那么与原图形上的点对应的位似图形上的点的
坐标为或.反之，由位似图形对应点的坐标，可以求
出它们的相似比.
图9
例4 （2024·浙江·中考）如图9，在平面直角坐标系
中，与是位似图形，位似中心为点 .
若点的对应点为，则点 的
对应点 的坐标为( ).
A
A. B. C. D.
思路点拨 根据点与点 的坐标求出相似比，再根据位似变换的性质计算即可.
提示：由，，得与 的相似比为2.因为点
B的坐标为，所以点B的对应点的坐标为 ，即
.
考点专练
图10
7.（2024·四川凉山·中考）如图10，一块面积为
的三角形硬纸板（记为 ）平行于投影
面时，在点光源的照射下形成的投影是 .
若，则 的面积是( ).
D
A. B. C. D.
图11
8.（2025·四川遂宁·中考模拟）在方格图中，以
格点为顶点的三角形叫作格点三角形．在
如图11所示的平面直角坐标系中，格点三角
形和格点三角形 成位似关系，则位
似中心的坐标为( ).
A
A. B. C. D.
考点五 与平移、对称、旋转、位似有关的网格作图
名师指导
1.平移（或旋转）作图的依据是平移（或旋转）的性质,一般步骤如下：
（1）确定平移的方向和距离（或确定旋转中心、旋转方向、旋转
角）;
（2）确定原图形中的关键点；
（3）利用平移（或旋转）的性质确定平移（或旋转）后所有关键
点的对应点；
（4）按原图形的顺序依次连接对应点，所得图形即为平移
（或旋转）后的图形.
2.画一个图形关于某条直线（或某点）对称的图形的一般步骤如下：
（1）确定原图形中的关键点（各顶点）;
（2）利用对称的性质确定所有关键点关于对称轴（或对称中心）
的对称点；
（3）按原图形的顺序依次连接对称点，所得图形与原图形关于该
直线（或该点）对称.
3.画位似图形的一般步骤如下：
（1）确定位似中心；
（2）分别连接并延长位似中心和原图的关键点，根据相似比，确
定所作位似图形的关键点；
（3）顺次连接上述所作各点，即可得到位似图形.
图12
例5 一题多问 如图12，在平面直角坐标系中，的顶点，，的坐标分别为 ，， ．
（1）画出与关于轴对称的，并写出点 的坐标.
解：如图68， 即为所求，
点的坐标是 .
图68
思路点拨 分别根据对称、平移、旋转、位似作图的方法及点的坐标特征，画出相应的图形，写出对应点的坐标.
（2）画出将 向左平移3个单位长度，再向上平移2个单位长度得到的，并写出点 的坐标.
图12
解：如图68，即为所求,点的坐标是 .
图68
图12
（3）画出将绕点顺时针旋转 得到的
，直接写出在旋转过程中，点到点 的路径的长.
解：如图68，即为所求，点 到旋转中心点的距离 .
所以在旋转过程中，点到点的路径的长为 .
图68
思路点拨 第（3）题，点到点 的路径长即为的长，该弧的半径为长，圆心角为 ；
（4）以点为位似中心，在第四象限内将按相似比 放大，得到，画出，并写出点 的坐标.
图12
图68
解：如图68，即为所求，点的坐标是 .
（5）在轴上找一点，使点到点， 的距离之和最短（不写作法，保留作图痕迹）.
图12
图68
解：如图68，点 即为所求.
思路点拨 第（5）题，点关于轴的对称点为 ，则连接，与轴的交点即为点；
（6）求 的值.
图12
图68
思路点拨 第（6）题，过点 作于点，构建直角三角形，在 中根据余弦的定义，即可求解.
解：由图可知， ，.
为等腰三角形.
如图68，过点作于点 ，则
.
在 中， ，
即．
考点专练
图13
9.（2025·安徽·模拟）如图13，在由边长为1个单位长
度的小正方形组成的网格中， 的顶点均为格点
（网格线的交点）.
（1）将线段 向右平移4个单位长度，再向下平移2
个单位长度，得到线段，画出线段 .
解：如图69，线段 即为所求．
图69
（2）以点为旋转中心，将按逆时针方向旋转 ，得到
，画出 .
图13
解：如图69， 即为所求．
图69
（3）在线段上描出点，使得为 的角平分线.（作图过程用虚线表示）
图13
图69
解：由勾股定理，得 ，则．
如图69，取的中点，连接 交于点，点 即为所求．
第31讲 图形的平移、对称、旋转与位似
靶向锤炼
靶向练
1.传统文化 剪纸是我国古老的民间艺术.下列剪纸图案中既是轴对称图
形，又是中心对称图形的是( ).
D
A. B.
C. D.
2.（2025·湖南邵阳·中考模拟）下列四种图形中，对称轴条数最多的是
( ).
B
A.等边三角形 B.圆 C.长方形 D.正方形
图1
3.（2025·内蒙古通辽·中考改编）如图1，用平移方法说
明平行四边形的面积公式时，若 平移
到，，，则 的平移距离为
( ).
B
A.3 B.4 C.5 D.12
图2
4.（2024·黑龙江绥化·中考）如图2，矩形 各顶
点的坐标分别为，，， .以
原点为位似中心，在 轴右侧将这个矩形缩小为原
来的，则顶点 在第一象限对应点的坐标是( ).
D
A. B. C.， D.，
图3
5.（2025·湖南益阳·中考模拟）如图3，在正方形
中，，为的中点，连接，将 绕
点按逆时针方向旋转 得到，连接 ，则
的长为______．
图4
6.如图4， 的顶点均在小正方形的顶点上，
每个小正方形的边长均为1个单位长度.
（1）画出与关于直线对称的 .
解：如图86， 即为所求.
图86
（2）画出 向左平移3个单位长度，再向下平移4个单位长度后得
到的 .
解：如图86， 即为所求.
图86
（3）画出将绕点逆时针旋转 后得到的 .
图4
解：如图86， 即为所求．
图86
攻坚练
7.如图5，四边形中，，，，且点 在
上，.将四边形沿折叠，点的对应点恰好落在
上，如图6所示.若，，则 的值为( ).
A. B. C. D.
提示：由折叠的性质，得 .又
，所以.由 ，
得.所以 .从
而得，即.所以 .由
【答案】B
，，得四边形是平行四边形.所以 .
所以.故 .
8.如图7（单位： ），一块矩形草坪中间有两条宽度相等的石子路
（每条石子路间距均匀），草坪（阴影部分）的面积是____ .
48
图7
9.（2025·江苏盐城·中考改编）如图8，在中， ，
，是的中点，连接，将绕点 旋转一定角
度得到，且在的右侧，连接.当时， 的长
为_______.
图8
提示：如图87，过点作于点.因为 ，，是的中点，所以， .从而得.由旋转的性质，得 .由，得 .所以 . 由勾股定理，得.所以 .
图87
10.开放性题（2025·浙江温州·中考模拟）如图9，在方格纸 中，每个小方
格的边长为1．已知格点 ，请按要求画格点三角形（顶点均在格点上）．
（1）在图9中画一个等腰三角形，使底边长为，点在 上，点
在上，再画出该三角形绕矩形的中心旋转 后的图形.
图9
解：（答案不唯一）如图88，
， 即为所求.
图88
（2）在图10中画一个，使 ，点在上，点在
上，再画出该三角形向右平移1个单位长度后的图形．
图10
解：如图89， ，R 即为所求．
图89
图11
11.（2024·黑龙江龙东·中考）如图11，在平面直角坐
标系中，各顶点的坐标分别为 ，
， .
（1）画出与关于轴对称的 ，并写
出点 的坐标.
解：如图90，即为所求，点的坐标为 .
图90
（2）画出绕点逆时针旋转 后得到的，并写出点
的坐标.
图11
解：如图90， 即为所求，点的坐标为 .
图90
图11
（3）在（2）的条件下，求点旋转到点 的过程中所经过的路径长（结果保留 ）.
图90
解：由勾股定理，得 .
由旋转的性质，得 .
故点旋转到点 的过程中所经过的路径长为 ．
拔尖练
图12
12.（2024·广西·中考）如图12， 中，
，的垂直平分线分别交 ，
于点，，平分 .
（1）求证： .
证明： 垂直平分， ，
平分， .
又 ， ．
图13
（2）如图13，将绕点 逆时针旋转得到
，旋转角为.连接， .
①求面积的最大值及此时旋转角 的度数，
并说明理由.
解：面积的最大值为，.
理由： ， ， .
在R中，，
.
∴ .如图91，过点作于点，过点 作于点，连接.
在 旋转的过程中，对应边，对应高，在中， ，在中，， .
如图92，当点，重合时，
取最大值，最大值为 ，
图91
图92
，即面积的最大值为.
此时 ，，三点共线， ．
图91
图92
②当是直角三角形时，请直接写出旋转角 的度数.
图13
提示：由旋转的性质，得 . 由， ，得当为直角三角形时， . 垂直平分， ， .如图93，当点与点重合时，点 恰好在的延长线上，满足 .此时 .
图93
图94
解： 为 或 .
如图94，当点 与点重合时，点恰好在的延长线上，满足 .此时 ．综上所述，当是直角三角形时， 为 或 ．