2026年中考《数学》复习课件 专题七 图形与变换-第32讲 与折叠、旋转有关的计算 (共52张PPT)

(共52张PPT)
复习讲义
第一篇 考点精讲
专题七 图形与变换
第32讲 与折叠、旋转有关的计算
聚焦核心
1.与折叠有关的计算
折叠问题（翻折变换）实质上就是________变换.折叠前后图形的形
状和大小不变，位置改变，对应____和对应____相等.将图形折叠时，经
常会出现直角，故在解答这类题时，可考虑运用__________列方程求解.
轴对称
边
角
勾股定理
2.与旋转有关的计算
旋转前后图形的形状和大小不变，位置改变，对应____和对应____
相等.根据旋转的性质，可得对应点到旋转中心的距离______，每对对
应点与旋转中心的连线所形成的角都______.旋转问题常结合等腰三角
形、全等三角形、相似三角形、特殊四边形等相关知识综合考查.
边
角
相等
相等
第32讲 与折叠、旋转有关的计算
案例分析
考点一 与折叠有关的计算
名师指导
图形的折叠问题常结合三角形或四边形进行考查，主要考查轴对称
和相关几何图形的性质.解决与折叠有关的问题的策略如下：（1）折痕
两侧的图形关于折痕成轴对称；（2）折叠之后，折痕所在的直线是对
应点的连线的垂直平分线；（3）寻找折叠前后隐含的位置关系和数量
关系，即寻找题目中隐含的等边、等角；（4）寻找图形中隐含的直角
三角形.
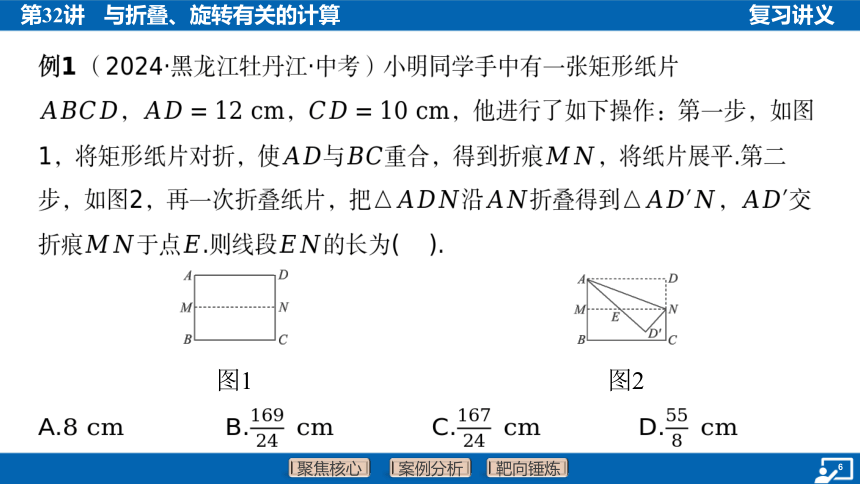
例1 （2024·黑龙江牡丹江·中考）小明同学手中有一张矩形纸片
，， ，他进行了如下操作：第一步，如图
1，将矩形纸片对折，使与重合，得到折痕 ，将纸片展平.第二
步，如图2，再一次折叠纸片，把沿折叠得到， 交
折痕于点.则线段 的长为( ).
图1
图2
A. B. C. D.
提示：由折叠的性质，得 ，，， ， .由，得.所以 . 由此可得.设，则.在 中，由勾股定理，得，即 .解得.故 .
【答案】B
图1
图2
思路点拨 观察图形发现，为，的边，要求线段 的
长，则考虑结合矩形的性质和折叠的性质，探究， 中三
边的数量关系和位置关系.
考点专练
图3
1.（2024·四川眉山·中考）如图3，在矩形 中，
，，点在上，把沿 折叠，
点恰好落在边上的点处，则 的值为
( ).
A. B. C. D.
图3
提示：由折叠的性质，得， .由
勾股定理，得 .所以
.在 中，
，由勾股定理，得
【答案】A
，即 .
解得.由此可得 .故
.
图4
2.（2025·安徽·中考改编）如图4，现有正方形纸片
，点，分别在边，上.将正方形
沿垂直于的直线折叠得到折痕，点， 分别
落在正方形所在平面内的点， 处，然后展
平纸片.
图4
（1）若点在边上，且 ，则
____（用含 的式子表示）.
提示：， ， ， ．
图4
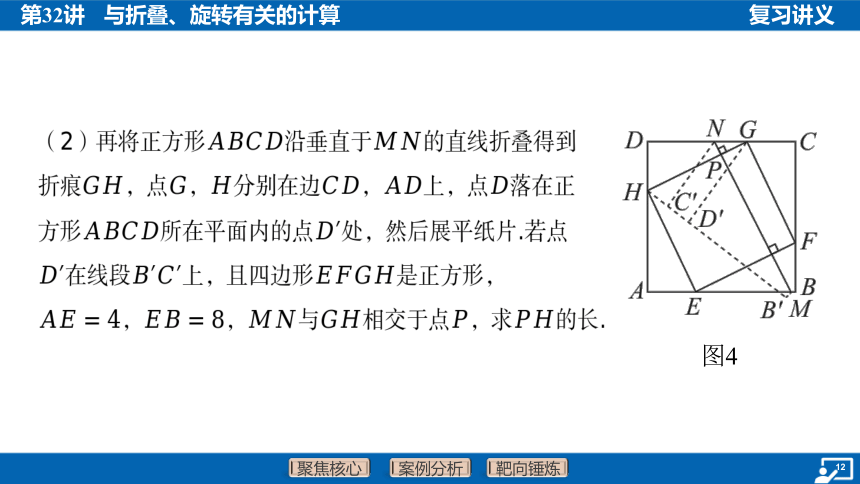
（2）再将正方形沿垂直于 的直线折叠得到
折痕，点，分别在边，上，点 落在正
方形所在平面内的点 处，然后展平纸片.若点
在线段上，且四边形 是正方形，
，，与相交于点，求 的长.
图78
解：如图78，设与相交于点 .
∵ 四边形和四边形是正方形，∴ ， ， .
∴ .
∴ .
在和 中，，，，
.
同理可得
∴ ，
，， 垂直平分
， .
由折叠的性质，得， ，
， .
∴ ，即 ，
.
∴ .
.
∴ ．
图78
考点二 与旋转有关的计算
名师指导
与旋转有关的问题常结合三角形、四边形进行考查，解决与旋转有
关的问题的策略如下：（1）利用旋转的性质，得到全等图形，对应点
到旋转中心的距离相等，对应点与旋转中心所连线段的夹角等于旋转角；
（2）旋转 时，即为中心对称，连接对应点的线段都经过对称中心
且被对称中心平分，对应线段平行且相等，对应角相等；（3）通过寻
找图形中存在的全等图形或相似图形，确定图形中几何元素之间的关系，
进而找到条件和结论间的联系，从而解决问题.
图5
例2 （2024·山东潍坊·中考）如图5，在平面直角坐
标系中，等边三角形的顶点的坐标为 ，点
，均在轴上.将绕顶点逆时针旋转 得
到，则点 的坐标为_ ___________.
思路点拨 求点的坐标，即求点到轴、轴的距离，则过点 作
轴于点，结合旋转的性质和等边三角形的性质求出， 的
长即可.
图5
提示：过点作轴于点.由题意，得 .因为
是等边三角形，，所以 ，
.在中， ，即
，解得 .由旋转的性质，得
.所以
，
.故， .
，
考点专练
图6
3.（2024·四川广元·中考）如图6，将绕点 顺时
针旋转 得到，点， 的对应点分别为点
，，连接，点恰好落在线段 上.如果
，，那么 的长为( ).
A. B. C.2 D.
图6
提示：由旋转的性质，得 ，
， .由
，得
，连接 ，由勾股定理，得
【答案】A
.在等腰直角三角形 中，
.
4.（2024·山东烟台·中考）在等腰直角三角形中， ，
，为直线上任意一点，连接.将线段绕点 按顺时针
方向旋转 得线段，连接 .
【尝试发现】
图7
（1）如图7，当点在线段上时，线段与 的
数量关系为____________.
图7
提示：过点作于点 .由旋转的性质，得， . . ， ， . ， ，
， .
【类比探究】
（2）当点在线段 的延长线上时，先在图8中补全图形，再探究线段
与 的数量关系并证明.
图8
解：补全图形如图79，.
证明：过点 作于点.
由旋转的性质，得 ， .
.
图79
图79
∵ ， ，
.
.
在 和中，， ，，
，
∵ ，
，即
∴ .
又 ， .
【联系拓展】
（3）已知，，请直接写出 的值.
提示：如图80，当点在的延长线上时，过点作于点 ，
同（2）可得，
. .如图81，当点 在
的延长线上时，过点作于点.
同理可得 ，
.
.
图80
图81
【答案】或 .
考点三 与折叠、旋转相关的综合计算
名师指导
当一道题中既有折叠又有旋转时，我们要分清图形的哪部分是由折
叠得到的，哪部分是由旋转得到的.折叠、旋转都能得到相等的角和边.
图9
例3 如图9，在中， ， ，将
沿折叠，点落在点处， ，再将 绕
点逆时针旋转，旋转角为.当 旋转至与
的一边平行时， 的度数为__________.
提示：由折叠的性质，得 ，从
而得 .当 时，
.所以 .
当时， ，所以
.故 .
图9
或
思路点拨 要分旋转后，和 两种情况
讨论.由折叠的性质可得相等的角，再结合旋转角的定
义和平行线的性质与判定可求旋转角的度数.
考点专练
图10
5.（2024·内蒙古呼和浩特·中考）如图10，在
中， ， ，将
沿折叠得到，将线段绕点 顺时针旋
转 得到线段，点为的中点，连接 ，
.若，则 的面积是( ).
A. B. C. D.
图82
提示：如图82，过点A作于点 .因为
， ，所以.
设，则 .从而得
， .所以
.由此可得 .由
，，得 .又
，所以.所以 .因为
，
，又由旋转的性
质，得， ，所以
.所以 .又
， ，所以
.所以 ，即
.过点作于点 ，所以
， .故
的面积
．
【答案】A
图82
第32讲 与折叠、旋转有关的计算
靶向锤炼
靶向练
图1
1.（2024·四川自贡·中考）如图1，在平面直角坐标系
中，，将绕点逆时针旋转 到
位置.则点 的坐标为( ).
A
A. B. C. D.
图2
2.如图2，将一张矩形纸条 折叠，折痕为
，折叠后点，分别落在点，处，
与相交于点.若 ，则 的
度数是( ).
D
A. B. C. D.
图3
3.如图3，在等边三角形中，，点是
的中点，将绕点逆时针旋转后得到 ，
连接，则 的长为( ).
C
A. B.6 C. D.
图4
4.（2024·山东威海·中考）将一张矩形纸片（矩形）按图4所示的方式折叠，使点 落在上的点处，折痕为，点落在点处， 交于点.若，，，则 的长为( ).
A. B. C.2 D.3
图4
提示：由四边形 是矩形，得
.在 中，
.由折叠的性质，得
， .
由 ，得
.又 ，所以
.所以， .由此可得，
， .所以
， .设
，则.在 中，
，即 .解得
.
【答案】B
图4
5.（2025·山东菏泽·中考模拟）如图5，是正方形内的一点，将
绕点按顺时针方向旋转 ，得到，连接，交于点 .若
，则____ .
80
图5
图6
6.（2024·四川雅安·中考）如图6，把矩形纸片 沿
对角线折叠，使点落在点处，与 相交于点
.若，，则 的值是_ __.
提示：由折叠的性质，得 .因为四边形
是矩形，所以.所以 .从而
得.所以.由此可得 .在
中，，即.解得 .
所以 .
图7
7.如图7，已知是正方形内一点，将
绕点按顺时针方向旋转 ，得到 .已知
， ，求 的度数.
解：由旋转的性质，得.∴ .
四边形为正方形， .
.
攻坚练
图8
8.（2024·黑龙江大庆·中考）如图8，在矩形 中，
，，是边的中点，是边 上任意一
点，将线段绕点按顺时针方向旋转 ，得到线段
，连接，则 周长的最小值为( ).
A.15 B. C. D.18
图106
提示：如图106，过点作，分别交 ，
于点，，过点作于点 .在矩形
中，，所以 .由此可得四
边形和四边形 都是矩形.所以
.由旋转的性质，得
， .所以
.从而得 .所以
. 所以点在平行于，且与 的距离为5的直线
上运动.作点关于直线的对称点，连接 交
直线于点，此时 的周长取得最小值，
最小值为.因为 ，
，所以
. 所以
.
【答案】B
图106
9.（2024·海南·中考）如图9，在矩形纸片中，， ，点
，分别在边，上，将纸片沿折叠，使点的对应点 在
边上，点的对应点为，则的最小值为___， 的最大值为__.
图9
提示：由折叠的性质，得.如图107，当时， 最小，
即最小，此时四边形是正方形.则 .如图108，
当点与点重合时，最大.此时点在 的垂直平分线上.在矩形纸
片中，，，则.所以 .由
，，得.所以 ，
即.解得.所以 ．
图107
图108
9.（2024·海南·中考）如图9，在矩形纸片中，， ，点
，分别在边，上，将纸片沿折叠，使点的对应点 在
边上，点的对应点为，则的最小值为___， 的最大值为__.
图9
6
10.如图10，在正方形中，，点在边上，且 .把
沿折叠得到，将绕点按逆时针方向旋转 ，
得到，连接，则 的长为_____.
图10
图10
提示：连接.由四边形 是正方形，得
.由折叠的性质，得
，．所以 .由旋转
的性质，得， ．所以
.从而得
．所以 ．所以
．所以．因为 ，所以
．在中，，故 ．
靶向练
图11
11.（2024·江苏无锡·中考）
【操作观察】
如图11，在四边形纸片
中，， ，
，， .折叠
四边形纸片，使得点的对应点始终落在上，点 的对应点为
，折痕分别与，交于点， .
， .
四边形是矩形.
，
，即.
【解决问题】
图11
（1）当点与点重合时，求 的长.
解：如图109，过点作，连接， .
图109
当点与点重合时，由折叠的性质，可得垂直平分 ，点与点重合，则有.
设 ，则.
在中， ，即，解得.
故 .
图109
（2）设直线与直线相交于点，当时，求 的长.
图11
图110
解：如图110，当点在上时，过点作于点 .
由（1）可知，，
.
， .
设，，则 .
根据折叠的性质，得
， .
在 中， ， .
由折叠的性质，得
， 5.
解得.
.
图110
如图111，当点在的延长线上时，同理可得.
在 中，设，则，， .
同理可得，
， 5.
解得.
.
综上所述，的值为或 ．
图111