2026年中考《数学》复习课件 专题七 图形与变换--第29讲 尺规作图 (共55张PPT)
文档属性
| 名称 | 2026年中考《数学》复习课件 专题七 图形与变换--第29讲 尺规作图 (共55张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-09 07:51:52 | ||
图片预览







文档简介
(共55张PPT)
复习讲义
第一篇 考点精讲
专题七 图形与变换
1.(2025·广西桂林·中考模拟)下列数学经典图形中,属于中心对称图形的
是( ).
A
A. B.
C. D.
图1
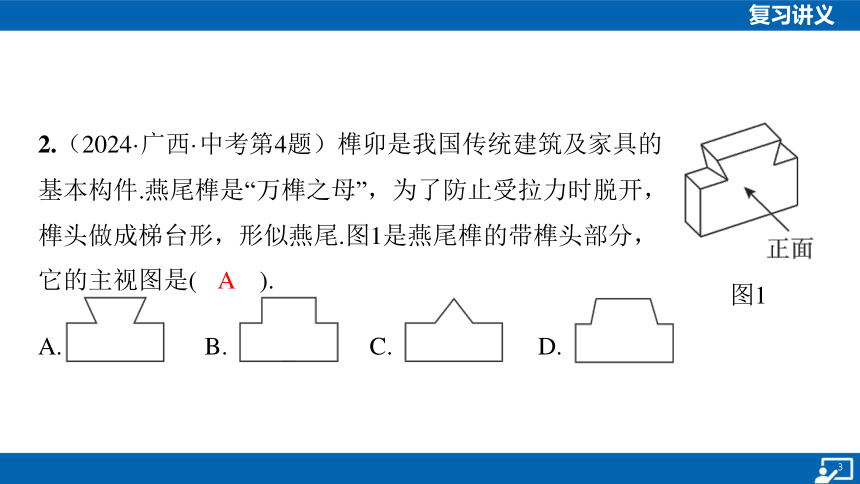
2.(2024·广西·中考第4题)榫卯是我国传统建筑及家具的
基本构件.燕尾榫是“万榫之母”,为了防止受拉力时脱开,
榫头做成梯台形,形似燕尾.图1是燕尾榫的带榫头部分,
它的主视图是( ).
A
A. B. C. D.
3.(2024·广西·中考第22题)如图2,在中, , .
图2
(1)尺规作图:作线段的垂直平分线,分别交,于点, .(要求:保留作图痕迹,不写作法,标明字母)
解:如图63,直线 为所求.
图63
(2)在(1)所作的图中,连接,若,求 的长.
图2
解:垂直平分线段,, ,
.在中,.
.
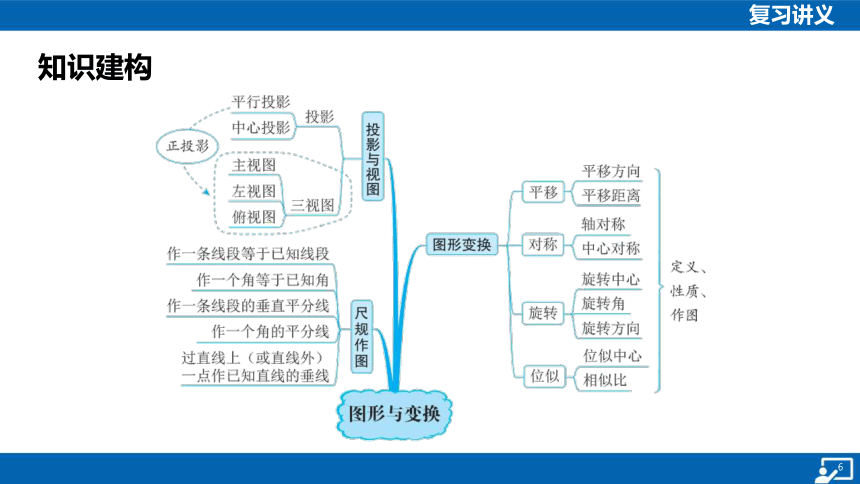
知识建构
第29讲 尺规作图
聚焦核心
1.尺规作图
用没有刻度的直尺和______作图,就是尺规作图.
圆规
2.五种基本作图
(1)作一条线段等于已知线段(已知:线段 ).
图形 ________________________________________________
作法 ①作射线
②以点为圆心,线段___的长为半径画弧,交射线 于点,则线段 就是所求作的线段
作图依据 圆上的点到圆心的距离等于______
半径
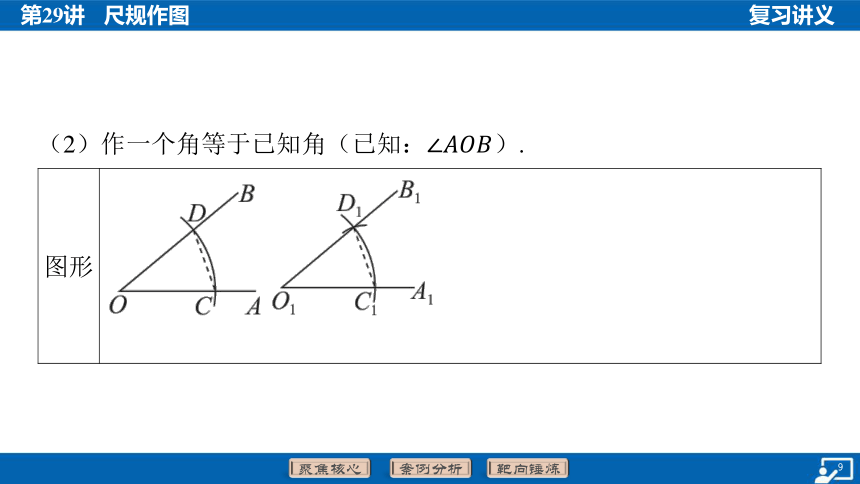
(2)作一个角等于已知角(已知: ).
图形 ____________________________________________________________________________________
作法 ①以点为圆心,任意长为半径画弧,分别交,于点,
②画一条射线,以点 为圆心,____长为半径画弧,交
于点
③以点 为圆心,____的长为半径画弧,与第②步中所画的弧相
交于点
④过点作射线,则 就是所求作的角
作图 依据 ①三边分别相等的两个三角形全等
②全等三角形的对应____相等
角
续表
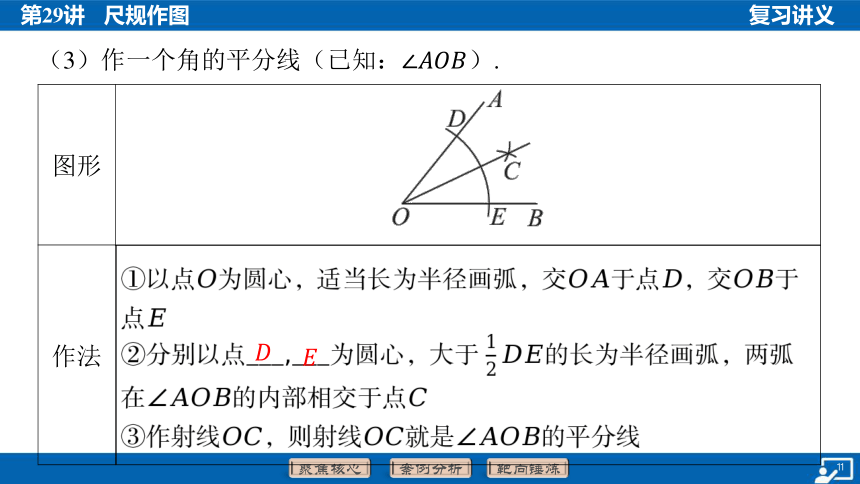
(3)作一个角的平分线(已知: ).
图形 _________________________________________
作法 ①以点为圆心,适当长为半径画弧,交于点,交 于点
②分别以点___,___为圆心,大于 的长为半径画弧,两弧
在的内部相交于点
③作射线,则射线就是 的平分线
作图 依据 ①三边分别相等的两个三角形全等
②全等三角形的对应____相等
角
续表
(4)作一条线段的垂直平分线(已知:线段 ).
图形 ______________________________________
作法 ①分别以点, 为圆心,大于_ ____的长为半径画弧,两弧相
交于, 两点
②作直线,则直线就是线段 的垂直平分线
作图依 据 ①与一条线段两个端点距离______的点,在这条线段的垂直平
分线上
②两点确定一条直线
相等
续表
(5)过一点作已知直线的垂线(已知:点和直线 ).
点在直线 上:
图形 __________________________________________
作法 ①以点为圆心,任意长为半径画弧,交于, 两点
②分别以点,为圆心,大于_____的长为半径向直线 的同
侧画弧,两弧相交于点
③作直线,则直线 就是所求作的垂线
作图 依据 ①等腰三角形底边上的高线、底边上的中线、顶角的平分线互相
重合(“三线合一”)
②两点确定一条直线
续表
点在直线 外:
图形 _____________________________________
作法 ①任意取一点,使点和点在直线 的两侧
②以点为圆心,____的长为半径画弧,交直线于点,
③分别以点,为圆心,大于_____的长为半径向直线 的同
侧画弧,两弧相交于点
④作直线,则直线 就是所求作的垂线
作图 依据 ①与一条线段两个端点距离______的点,在这条线段的垂直平分
线上
②两点确定一条直线
相等
续表
提醒:《义务教育数学课程标准(2022年版)》要求的12种尺规作图
(1)作一个角等于已知角;
(2)作一个角的平分线;
(3)作一条线段的垂直平分线;
(4)过一点作已知直线的垂线;
(5)过直线外一点作这条直线的平行线(新增);
(6)已知三边、两边及其夹角、两角及其夹边作三角形;
(7)已知底边及底边上的高线作等腰三角形;
(8)已知一直角边和斜边作直角三角形;
(9)过不在同一直线上的三点作圆;
(10)作三角形的外接圆、内切圆;
(11)作圆的内接正方形和内接正六边形;
(12)过圆外一点作圆的切线(新增,选学).
第29讲 尺规作图
案例分析
考点一 基本作图的认识
名师指导 熟练掌握五种基本作图的方法和作图依据,是用尺规作图的基础.
图1
例1 (2025·广东深圳·中考模拟)在如图1
的三个图形中,根据尺规作图的痕迹,
能判断射线平分 的是( ).
A.①② B.①③
C.②③ D.只有①
思路点拨 根据基本作图的方法对图①②的作法进行判断.图③由作法可得, ,若能证明,则可推出 平分 .
图1
提示:根据基本作图可判断题图①中 为
的平分线,题图②中为 边上的中线. 题图③中,由, ,
,得 .所以
【答案】B
.又, ,所以
.所以.又, .所以
.由此可得,.故为 的平分线.
考点专练
图2
1.(2024·河北·中考)观察图2中尺规作图的痕迹,
可得线段一定是 的( ).
B
A.角平分线 B.高线 C.中位线 D.中线
考点二 根据尺规作图的痕迹、步骤判断结论及计算
名师指导 这类问题常以五种基本作图:“作一条线段等于已知线段”“作
一个角等于已知角”“作一个角的平分线”“作一条线段的垂直平分线”“过
一点作已知直线的垂线”为背景,考查“等边对等角”的性质,平行线的
判定与性质,角平分的定义与性质,“线段垂直平分线上的点到线段两
端距离相等”的性质,等腰三角形“三线合一”的性质等.
图3
例2 (2025·四川成都·中考模拟)如图3,在 中,
按以下步骤作图:①以点 为圆心,以适当的长为
半径作弧,分别交,于点, ;②分别以
,为圆心,以大于 的长为半径作弧,两弧
在内交于点;③作射线,交于点 ,
A. B.
C. D.
交的延长线于点.若, ,则下列结论错误的是( ).
思路点拨 由作图可知是 的平分线,再结合平行四边形的性质对结论逐一进行判断.
图3
提示:由作法得平分,即 .
故选项A中结论是正确的.因为四边形 为平行
四边形,所以, ,
,.从而得 .所以
.因此 .所以
【答案】D
,即 .故选项B中结论是正确的.由
,得.又,所以 .所以
.故选项C中结论是正确的.由,得 .故选
项D中结论是错误的.
考点专练
图4
2.(2024·吉林长春·中考)如图4,在中,
是边的中点.按下列要求作图:①以点 为圆心、
适当长为半径画弧,交线段于点,交于点 ;
②以点为圆心、的长为半径画弧,交线段
于点;③以点为圆心、 的长为半径画弧,交
前一条弧于点,点与点在直线 同侧;④作
直线,交于点 .下列结论不一定成立的是 ( ).
A. B.
C. D.
图4
√
考点三 尺规作图及相关的计算与证明
名师指导 与尺规作图相关的计算与证明题是近两年中考的热点,这类问
题除了要按要求进行尺规作图,还要利用几何知识进行计算或证明.解
题时要根据尺规作图所蕴含的结论及相应的几何图形性质进行分析.
例3 (2024·广东广州·中考)如图5,在中, .
图5
(1)尺规作图:作边上的中线 .(保留作图痕迹,不写作法)
图5
解:如图64,线段 即为所求.
图64
思路点拨(1)作线段的垂直平分线交于点,连接 ,即为边上的中线.
(2)在(1)所作的图中,将中线绕点逆时针旋转 得到 ,连接,.求证:四边形 是矩形.
图5
思路点拨 (2)已知 ,则只要证明四边形是平行四边形,即可证得结论.由(1)可知是 的中点,且,是四边形 的两条对角线,结合旋转的性质,可由对角线互相平分的四边形是平行四边形判定四边形 是平行四边形.
图64
证明:如图64,是的中点,
是由绕点逆时针旋转得到的, ,且,,在同一直线上.
四边形是平行四边形.
, 四边形 是矩形.
考点专练
3.尺规作图:如图6,已知,请根据“”基本事实作出 ,
使 .(保留作图痕迹,不写做法)
图6
解:如图65, 即为所求.
图65
4.新课标·新要求 下面是小红设计的“过圆外一点作圆的一条切线”的尺规作图的过程.
已知:如图7,及圆外一点 .
图7
求作:过点作 的一条切线.
作法:①连接;②作的垂直平分线,交于点;③以点
为圆心,的长为半径画弧,交于点;④作直线.直线 即为
所求作的一条切线.
根据上述尺规作图的过程,回答以下问题:
(1)使用无刻度的直尺和圆规,依作法补全图形(保留作图痕迹).
图7
解:补全图形如图66.
图66
图7
(2)连接 ,在该作图中,可以得到
____ ,依据是直径所对的圆周角等于
_________.
90
第29讲 尺规作图
靶向锤炼
靶向练
图1
1.(2025·广西百色·中考模拟)图1是求作线段 的中点的作
图痕迹,则下列结论不一定成立的是( ).
A
A. B. C. D.
2.(2024·四川自贡·中考)如图2,以点 为圆心,适当的长为半径画弧,
交两边于点,,再分别以点,为圆心, 的长为半径画弧,
两弧交于点,连接,.若 ,则 的度数是( ).
A
图2
A. B. C. D.
图3
3.(2024·北京·中考)下面是“作一个角使
其等于 ”的尺规作图方法.①如图3,
以点 为圆心,任意长为半径画弧,分别
交,于点,;②作射线 ,以
点为圆心,的长为半径画弧,交
于点,以点为圆心,的长为半径画弧,两弧交于点;③过点
作射线,则.上述方法通过判定 得
到,其中判定 的依据是 ( ).
A.三边分别相等的两个三角形全等
B.两边及其夹角分别相等的两个三角形全等
C.两角及其夹边分别相等的两个三角形全等
D.两角分别相等且其中一组等角的对边相等的两个三角形全等
图3
√
图4
4. 观察图4的作图痕迹,直线 与
的位置关系为_________,依据是同位角相等,
两直线平行
图5
5.(2024·黑龙江齐齐哈尔·中考)如图5,在平面直角
坐标系中,以点为圆心,适当长为半径画弧,交 轴
的正半轴于点,交轴的正半轴于点 ,再分别以点
,为圆心,大于 的长为半径画弧,两弧在第
2
一象限交于点,画射线,若点的坐标为,则 ___.
6.(2025·蚌埠·中考模拟)如图6,在中, , .
图6
(1)在斜边上求作线段,使,连接 (要求:尺规作图,并保留作图痕迹,不写作法,标明字母)
解:如图79,线段 即为所求.
图79
(2)已知,求 的长.
图6
解: , ,
,∴
,即为的中点.
又 ,
.
攻坚练
7.新课标·新要求 小明想通过尺规作图确定经过三角形三个顶点的圆的
圆心 ,下面四种作图方式中可选择( ).
C
A. B. C. D.
提示:作出三角形三边垂直平分线的交点,即可找到其外接圆的圆心.
图7
8.(2024·山东泰安·中考)如图7,在 中,
,分别以顶点,为圆心,大于 的
长为半径画弧,两弧分别相交于点和点 ,作直线
分别与,交于点和点;以点 为圆心,任
意长为半径画弧,分别交,于点和点 ,再分
别以点,为圆心,大于 的长为半径画弧,两弧
A.1 B.2 C.3 D.4
交于点,作射线.若射线恰好经过点 ,则有下列四个结论:
,垂直平分线段, ,
.其中,正确结论的个数有( ).
图7
提示:由作图可知垂直平分线段, 平分
,由此可得,, ,
.因为 ,所以
.从而得 ,
.因为,所以.所以 垂直
平分线段.故①②正确.因为, ,
【答案】D
所以.从而得.因为 ,所以
.由此可得 .故③④正确.
9.(2024·新疆·中考)如图8,已知 .
图8
(1)尺规作图:请用无刻度的直尺和圆规,作的平分线交于点 .(保留作图痕迹,不写作法)
解:如图80, 即为所求.
图80
(2)在(1)的条件下,求证: 是等腰三角形.
图8
证明: 为的平分线,
四边形 为平行四边形,
是等腰三角形.
拔尖练
10.(2024·江苏扬州·中考)如图9,已知及边上一点 .
图9
(1)用无刻度直尺和圆规在射线上求作点,使得 .(保留作图痕迹,不写作法)
解:如图81,点 即为所求.
图81
(2)在(1)的条件下,以点为圆心,以 的长为半径的圆交射线
于点,用无刻度直尺和圆规在射线上求作点,使点到点 的
距离与点到射线 的距离相等.(保留作图痕迹,不写作法)
图9
【答案】如图81,点, 即为所求.
图81
(3)在的条件下,已知,,求 的长.
图9
图81
解:由作图可知,点 ,,在以点为圆心的圆上.
为 的直径, .
在 中,,可设, ,则.
如图81,过点 作于点.
由(2)知,平分 , .
在中, ,, .
解得
.
图81
复习讲义
第一篇 考点精讲
专题七 图形与变换
1.(2025·广西桂林·中考模拟)下列数学经典图形中,属于中心对称图形的
是( ).
A
A. B.
C. D.
图1
2.(2024·广西·中考第4题)榫卯是我国传统建筑及家具的
基本构件.燕尾榫是“万榫之母”,为了防止受拉力时脱开,
榫头做成梯台形,形似燕尾.图1是燕尾榫的带榫头部分,
它的主视图是( ).
A
A. B. C. D.
3.(2024·广西·中考第22题)如图2,在中, , .
图2
(1)尺规作图:作线段的垂直平分线,分别交,于点, .(要求:保留作图痕迹,不写作法,标明字母)
解:如图63,直线 为所求.
图63
(2)在(1)所作的图中,连接,若,求 的长.
图2
解:垂直平分线段,, ,
.在中,.
.
知识建构
第29讲 尺规作图
聚焦核心
1.尺规作图
用没有刻度的直尺和______作图,就是尺规作图.
圆规
2.五种基本作图
(1)作一条线段等于已知线段(已知:线段 ).
图形 ________________________________________________
作法 ①作射线
②以点为圆心,线段___的长为半径画弧,交射线 于点,则线段 就是所求作的线段
作图依据 圆上的点到圆心的距离等于______
半径
(2)作一个角等于已知角(已知: ).
图形 ____________________________________________________________________________________
作法 ①以点为圆心,任意长为半径画弧,分别交,于点,
②画一条射线,以点 为圆心,____长为半径画弧,交
于点
③以点 为圆心,____的长为半径画弧,与第②步中所画的弧相
交于点
④过点作射线,则 就是所求作的角
作图 依据 ①三边分别相等的两个三角形全等
②全等三角形的对应____相等
角
续表
(3)作一个角的平分线(已知: ).
图形 _________________________________________
作法 ①以点为圆心,适当长为半径画弧,交于点,交 于点
②分别以点___,___为圆心,大于 的长为半径画弧,两弧
在的内部相交于点
③作射线,则射线就是 的平分线
作图 依据 ①三边分别相等的两个三角形全等
②全等三角形的对应____相等
角
续表
(4)作一条线段的垂直平分线(已知:线段 ).
图形 ______________________________________
作法 ①分别以点, 为圆心,大于_ ____的长为半径画弧,两弧相
交于, 两点
②作直线,则直线就是线段 的垂直平分线
作图依 据 ①与一条线段两个端点距离______的点,在这条线段的垂直平
分线上
②两点确定一条直线
相等
续表
(5)过一点作已知直线的垂线(已知:点和直线 ).
点在直线 上:
图形 __________________________________________
作法 ①以点为圆心,任意长为半径画弧,交于, 两点
②分别以点,为圆心,大于_____的长为半径向直线 的同
侧画弧,两弧相交于点
③作直线,则直线 就是所求作的垂线
作图 依据 ①等腰三角形底边上的高线、底边上的中线、顶角的平分线互相
重合(“三线合一”)
②两点确定一条直线
续表
点在直线 外:
图形 _____________________________________
作法 ①任意取一点,使点和点在直线 的两侧
②以点为圆心,____的长为半径画弧,交直线于点,
③分别以点,为圆心,大于_____的长为半径向直线 的同
侧画弧,两弧相交于点
④作直线,则直线 就是所求作的垂线
作图 依据 ①与一条线段两个端点距离______的点,在这条线段的垂直平分
线上
②两点确定一条直线
相等
续表
提醒:《义务教育数学课程标准(2022年版)》要求的12种尺规作图
(1)作一个角等于已知角;
(2)作一个角的平分线;
(3)作一条线段的垂直平分线;
(4)过一点作已知直线的垂线;
(5)过直线外一点作这条直线的平行线(新增);
(6)已知三边、两边及其夹角、两角及其夹边作三角形;
(7)已知底边及底边上的高线作等腰三角形;
(8)已知一直角边和斜边作直角三角形;
(9)过不在同一直线上的三点作圆;
(10)作三角形的外接圆、内切圆;
(11)作圆的内接正方形和内接正六边形;
(12)过圆外一点作圆的切线(新增,选学).
第29讲 尺规作图
案例分析
考点一 基本作图的认识
名师指导 熟练掌握五种基本作图的方法和作图依据,是用尺规作图的基础.
图1
例1 (2025·广东深圳·中考模拟)在如图1
的三个图形中,根据尺规作图的痕迹,
能判断射线平分 的是( ).
A.①② B.①③
C.②③ D.只有①
思路点拨 根据基本作图的方法对图①②的作法进行判断.图③由作法可得, ,若能证明,则可推出 平分 .
图1
提示:根据基本作图可判断题图①中 为
的平分线,题图②中为 边上的中线. 题图③中,由, ,
,得 .所以
【答案】B
.又, ,所以
.所以.又, .所以
.由此可得,.故为 的平分线.
考点专练
图2
1.(2024·河北·中考)观察图2中尺规作图的痕迹,
可得线段一定是 的( ).
B
A.角平分线 B.高线 C.中位线 D.中线
考点二 根据尺规作图的痕迹、步骤判断结论及计算
名师指导 这类问题常以五种基本作图:“作一条线段等于已知线段”“作
一个角等于已知角”“作一个角的平分线”“作一条线段的垂直平分线”“过
一点作已知直线的垂线”为背景,考查“等边对等角”的性质,平行线的
判定与性质,角平分的定义与性质,“线段垂直平分线上的点到线段两
端距离相等”的性质,等腰三角形“三线合一”的性质等.
图3
例2 (2025·四川成都·中考模拟)如图3,在 中,
按以下步骤作图:①以点 为圆心,以适当的长为
半径作弧,分别交,于点, ;②分别以
,为圆心,以大于 的长为半径作弧,两弧
在内交于点;③作射线,交于点 ,
A. B.
C. D.
交的延长线于点.若, ,则下列结论错误的是( ).
思路点拨 由作图可知是 的平分线,再结合平行四边形的性质对结论逐一进行判断.
图3
提示:由作法得平分,即 .
故选项A中结论是正确的.因为四边形 为平行
四边形,所以, ,
,.从而得 .所以
.因此 .所以
【答案】D
,即 .故选项B中结论是正确的.由
,得.又,所以 .所以
.故选项C中结论是正确的.由,得 .故选
项D中结论是错误的.
考点专练
图4
2.(2024·吉林长春·中考)如图4,在中,
是边的中点.按下列要求作图:①以点 为圆心、
适当长为半径画弧,交线段于点,交于点 ;
②以点为圆心、的长为半径画弧,交线段
于点;③以点为圆心、 的长为半径画弧,交
前一条弧于点,点与点在直线 同侧;④作
直线,交于点 .下列结论不一定成立的是 ( ).
A. B.
C. D.
图4
√
考点三 尺规作图及相关的计算与证明
名师指导 与尺规作图相关的计算与证明题是近两年中考的热点,这类问
题除了要按要求进行尺规作图,还要利用几何知识进行计算或证明.解
题时要根据尺规作图所蕴含的结论及相应的几何图形性质进行分析.
例3 (2024·广东广州·中考)如图5,在中, .
图5
(1)尺规作图:作边上的中线 .(保留作图痕迹,不写作法)
图5
解:如图64,线段 即为所求.
图64
思路点拨(1)作线段的垂直平分线交于点,连接 ,即为边上的中线.
(2)在(1)所作的图中,将中线绕点逆时针旋转 得到 ,连接,.求证:四边形 是矩形.
图5
思路点拨 (2)已知 ,则只要证明四边形是平行四边形,即可证得结论.由(1)可知是 的中点,且,是四边形 的两条对角线,结合旋转的性质,可由对角线互相平分的四边形是平行四边形判定四边形 是平行四边形.
图64
证明:如图64,是的中点,
是由绕点逆时针旋转得到的, ,且,,在同一直线上.
四边形是平行四边形.
, 四边形 是矩形.
考点专练
3.尺规作图:如图6,已知,请根据“”基本事实作出 ,
使 .(保留作图痕迹,不写做法)
图6
解:如图65, 即为所求.
图65
4.新课标·新要求 下面是小红设计的“过圆外一点作圆的一条切线”的尺规作图的过程.
已知:如图7,及圆外一点 .
图7
求作:过点作 的一条切线.
作法:①连接;②作的垂直平分线,交于点;③以点
为圆心,的长为半径画弧,交于点;④作直线.直线 即为
所求作的一条切线.
根据上述尺规作图的过程,回答以下问题:
(1)使用无刻度的直尺和圆规,依作法补全图形(保留作图痕迹).
图7
解:补全图形如图66.
图66
图7
(2)连接 ,在该作图中,可以得到
____ ,依据是直径所对的圆周角等于
_________.
90
第29讲 尺规作图
靶向锤炼
靶向练
图1
1.(2025·广西百色·中考模拟)图1是求作线段 的中点的作
图痕迹,则下列结论不一定成立的是( ).
A
A. B. C. D.
2.(2024·四川自贡·中考)如图2,以点 为圆心,适当的长为半径画弧,
交两边于点,,再分别以点,为圆心, 的长为半径画弧,
两弧交于点,连接,.若 ,则 的度数是( ).
A
图2
A. B. C. D.
图3
3.(2024·北京·中考)下面是“作一个角使
其等于 ”的尺规作图方法.①如图3,
以点 为圆心,任意长为半径画弧,分别
交,于点,;②作射线 ,以
点为圆心,的长为半径画弧,交
于点,以点为圆心,的长为半径画弧,两弧交于点;③过点
作射线,则.上述方法通过判定 得
到,其中判定 的依据是 ( ).
A.三边分别相等的两个三角形全等
B.两边及其夹角分别相等的两个三角形全等
C.两角及其夹边分别相等的两个三角形全等
D.两角分别相等且其中一组等角的对边相等的两个三角形全等
图3
√
图4
4. 观察图4的作图痕迹,直线 与
的位置关系为_________,依据是同位角相等,
两直线平行
图5
5.(2024·黑龙江齐齐哈尔·中考)如图5,在平面直角
坐标系中,以点为圆心,适当长为半径画弧,交 轴
的正半轴于点,交轴的正半轴于点 ,再分别以点
,为圆心,大于 的长为半径画弧,两弧在第
2
一象限交于点,画射线,若点的坐标为,则 ___.
6.(2025·蚌埠·中考模拟)如图6,在中, , .
图6
(1)在斜边上求作线段,使,连接 (要求:尺规作图,并保留作图痕迹,不写作法,标明字母)
解:如图79,线段 即为所求.
图79
(2)已知,求 的长.
图6
解: , ,
,∴
,即为的中点.
又 ,
.
攻坚练
7.新课标·新要求 小明想通过尺规作图确定经过三角形三个顶点的圆的
圆心 ,下面四种作图方式中可选择( ).
C
A. B. C. D.
提示:作出三角形三边垂直平分线的交点,即可找到其外接圆的圆心.
图7
8.(2024·山东泰安·中考)如图7,在 中,
,分别以顶点,为圆心,大于 的
长为半径画弧,两弧分别相交于点和点 ,作直线
分别与,交于点和点;以点 为圆心,任
意长为半径画弧,分别交,于点和点 ,再分
别以点,为圆心,大于 的长为半径画弧,两弧
A.1 B.2 C.3 D.4
交于点,作射线.若射线恰好经过点 ,则有下列四个结论:
,垂直平分线段, ,
.其中,正确结论的个数有( ).
图7
提示:由作图可知垂直平分线段, 平分
,由此可得,, ,
.因为 ,所以
.从而得 ,
.因为,所以.所以 垂直
平分线段.故①②正确.因为, ,
【答案】D
所以.从而得.因为 ,所以
.由此可得 .故③④正确.
9.(2024·新疆·中考)如图8,已知 .
图8
(1)尺规作图:请用无刻度的直尺和圆规,作的平分线交于点 .(保留作图痕迹,不写作法)
解:如图80, 即为所求.
图80
(2)在(1)的条件下,求证: 是等腰三角形.
图8
证明: 为的平分线,
四边形 为平行四边形,
是等腰三角形.
拔尖练
10.(2024·江苏扬州·中考)如图9,已知及边上一点 .
图9
(1)用无刻度直尺和圆规在射线上求作点,使得 .(保留作图痕迹,不写作法)
解:如图81,点 即为所求.
图81
(2)在(1)的条件下,以点为圆心,以 的长为半径的圆交射线
于点,用无刻度直尺和圆规在射线上求作点,使点到点 的
距离与点到射线 的距离相等.(保留作图痕迹,不写作法)
图9
【答案】如图81,点, 即为所求.
图81
(3)在的条件下,已知,,求 的长.
图9
图81
解:由作图可知,点 ,,在以点为圆心的圆上.
为 的直径, .
在 中,,可设, ,则.
如图81,过点 作于点.
由(2)知,平分 , .
在中, ,, .
解得
.
图81
同课章节目录
