广东省汕头市金山中学2024-2025学年高一下学期期末考试物理试卷(含解析)
文档属性
| 名称 | 广东省汕头市金山中学2024-2025学年高一下学期期末考试物理试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 667.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-07-09 12:18:14 | ||
图片预览




文档简介
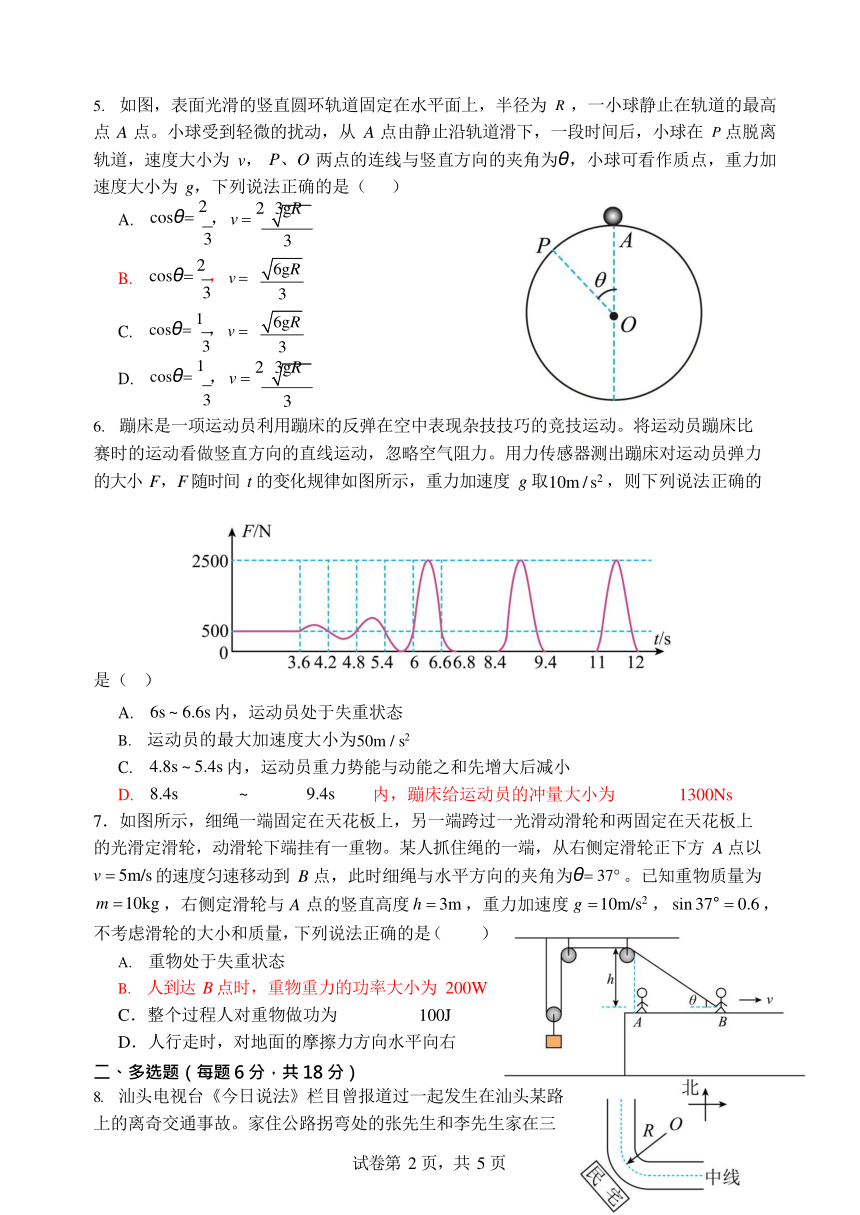
2024 级高一第二学期期末测试
物理科试卷
一、单选题(每题 4 分,共 28 分)
如图所示,曲线 AB 为一质点的运动轨迹,某人在曲线上 P 点做出质点在经过该处时其受力的 8 个可能方向,正确的是
只有方向 2、3、4 可能
只有方向 1、3 可能
只有方向 1、2、3、4、5 可能
D.8 个方向都可能 2.牛顿发现了万有引力定律,并给出了物体间引力大小表达式
F G m1m2 ,但没有给出引力常量 G 的具体取值。如图为人类第一次在实验室测量出万有
r 2
引力常量的实验示意图,通过此套装置比较精确测量出了万有引力常量数值,引力常量的精确测定对深入研究物体之间相互作用规律更有意义。以下说
法正确的是( ) A.图示引力常量测量实验中运用了放大法 B.根据万有引力定律表达式,当 r→0 时,物体间引力将趋于无穷大 C.图示实验中的大球对小球引力大于小球对大球引力 D.伽利略首先测量出了万有引力常量数值
3.下面五幅图是网球竖直下落与地面碰撞后又弹起的过程。 从左往右,第二幅图是网球刚与地面接触时拍摄,第三幅图是网球形变量最大时拍摄,忽略空气阻力和网球与地面碰撞的能量损失。 下列说法正确的是( )
A.拍摄第二幅图时,网球的动能最大 B.网球与地面碰撞整个过程中,弹力的冲量等于网球动量的改变量 C.网球与地面碰撞过程中,地面对网球的弹力不做功 D.网球与地面碰撞整个过程中,地面对网球的弹力先做正功后做负功
4.2024 年科学家发现了一颗距离地球 40 光年的类地行星 Gliese12b,这颗行星的发现引发了全球对“第二颗地球”的热议。Gliese12b 体积和地球差不多,质量约为地球的 4 倍。将某物体分别在 Gliese12b 表面与地球表面水平抛出,若水平抛出的高度和初速度均相同,则物体第一次落地时水平距离之比约为( )
A.4∶1 B.1∶4 C.1∶2 D.2∶1
如图,表面光滑的竖直圆环轨道固定在水平面上,半径为 R ,一小球静止在轨道的最高点 A 点。小球受到轻微的扰动,从 A 点由静止沿轨道滑下,一段时间后,小球在 P 点脱离轨道,速度大小为 v, P、O 两点的连线与竖直方向的夹角为θ,小球可看作质点,重力加速度大小为 g,下列说法正确的是( )
cosθ 2 , v 2 3gR
3
cosθ 2 , v
3
cosθ 1 , v
3
3
6gR 3
6gR 3
cosθ 1 , v 2 3gR
3 3
蹦床是一项运动员利用蹦床的反弹在空中表现杂技技巧的竞技运动。将运动员蹦床比赛时的运动看做竖直方向的直线运动,忽略空气阻力。用力传感器测出蹦床对运动员弹力的大小 F,F 随时间 t 的变化规律如图所示,重力加速度 g 取10m / s2 ,则下列说法正确的是( )
6s ~ 6.6s 内,运动员处于失重状态
运动员的最大加速度大小为50m / s2
4.8s ~ 5.4s 内,运动员重力势能与动能之和先增大后减小
8.4s ~ 9.4s 内,蹦床给运动员的冲量大小为 1300Ns 7.如图所示,细绳一端固定在天花板上,另一端跨过一光滑动滑轮和两固定在天花板上的光滑定滑轮,动滑轮下端挂有一重物。某人抓住绳的一端,从右侧定滑轮正下方 A 点以 v 5m/s 的速度匀速移动到 B 点,此时细绳与水平方向的夹角为θ 37 。已知重物质量为
m 10kg ,右侧定滑轮与 A 点的竖直高度 h 3m ,重力加速度 g 10m/s2 , sin 37° 0.6 ,不考虑滑轮的大小和质量,下列说法正确的是( )
重物处于失重状态
人到达 B 点时,重物重力的功率大小为 200W C.整个过程人对重物做功为 100J D.人行走时,对地面的摩擦力方向水平向右
二、多选题(每题 6 分,共 18 分)
汕头电视台《今日说法》栏目曾报道过一起发生在汕头某路上的离奇交通事故。家住公路拐弯处的张先生和李先生家在三
个月内连续遭遇了七次大卡车侧翻在自家门口的场面,第八次有辆卡车冲撞进李先生家,造成三死一伤和房屋严重损毁的血腥惨案.经公安部门和交通部门协力调查,画出的现场 示意图如图所示。交警根据图示作出以下判断,你认为正确的是( )
由图可知汽车在拐弯时发生侧翻是因为车做离心运动 B.由图可知汽车在拐弯时发生侧翻是因为车做向心运动 C.公路在设计上可能内(东北)高外(西南)低 D.公路在设计上可能外(西南)高内(东北)低
9.2024 年 11 月 23 日,2024 中国足协杯决赛在温州奥体中心举行。如图甲所示,一足球运动员在水平草地上练习传高空球。如果他在同一地点把同一个足球前后两次斜向上踢出,第一次足球落在草地上的M 点,第二次落在草地上的 N 点,足球两次在空中运动的最大 高度相等,且ON 3OM ,空气阻力不计,如图乙所示。下列说法正确的是( )
足球第二次被踢出时的初动能一定是第一次的 9 倍 B.足球两次在空中运动的时间不相同 C.足球两次落地时的速度与水平方向夹角的关系为 tanθM=3tanθN D.足球第二次被踢出时的初速度的水平分量是第一次的 3 倍
如题图甲所示,竖直平面内固定一光滑的半圆形轨道 ABC,B 点为 AC 轨道的中点, 小球以一定的初速度从最低点 A 冲上轨道,小球在半圆形轨道上从 A 运动到 C 的过程中,其速度的平方与对应高度的关系图像如图乙。已知小球在最高点 C 受到轨道的弹力大小为 11N,不计空气阻力,g=10m/s2,则( )
A.图乙中 x 为 9m2 s-2 B.小球质量为0.5kg
C.小球在 A 点所受支持力为 36N D.小球在 B 点所受合力大于 26N
三、实验题(每空 2 分,共 16 分)
某实验小组应用下图装置探究动量守恒定律,光滑斜面与水平面间平滑连接,质量为
M 的小球 A 从斜面上高 h 处滑下,小球 A 与质量为 m 的静止滑块 B 对心碰撞并一起向前运动距离 s 后停下来。A、B 与水平地面间的动摩擦因数均为 μ ,重力加速度为 g。
(1)A 物体到达地面瞬间的速度为 ;
A、B 碰后瞬间的速度为 ;
若 A、B 碰撞的过程中动量守恒,应满足的关系式为 。(应用题目中所给字母进行表示)
某同学用如图(a)所示的装置验证机械能守恒定律。不可伸长的轻绳绕过轻质定滑轮,轻绳两端分别连接物块 P 与感光细钢柱 K,两者质钢柱量均为m 0.140kg ,钢柱 K下端与质量为M 0.200kg 的物块 Q 相连。铁架电动机台下部固定一个电动机,电动机竖直转轴上装一支激光笔,电动机带动激光笔绕转轴在水平面内匀速转动,每转一周激光照
经判断系统由静止释放时激光笔光束恰好经过 O 点。参照图(b),在 OE 段,系统动能的增加量Δ Ek ,重力势能的减少量Δ Ep ;比较两者关系可判断系统机械能是否守恒。(计算结果均保留 3 位有效数字)
选取相同的另一感光细钢柱 K,若初始时激光笔对准 K 上某点,开启电动机的同时系统由静止释放,电动机的角速度按如图(c)所示的规律变化,图像斜率为 k,记录下如图
(d)所示的感光痕迹,其中两相邻感光痕迹间距均为 d。若验证得到表达式 k= 即可证明系统在运动过程中机械能守恒(用含字母 M、m、d、k、g、π 的表达式表示)。
四、计算题(共 38 分)
13.(本题 10 分)一宇航员在某未知星球的表面上做平抛运动实验:在离地面 h 高处让小球以某一初速度水平抛出,他测出小球落地点与抛出点的水平距离为 x 和落地时间 t,又已知该星球的半径为 R,已知万有引力常量为 G,求:
该星球表面的重力加速度 g
该星球的质量 M
该星球的第一宇宙速度 v(最后结果必须用题中已知物理量表示)
14.(本题 10 分)如图所示 AP 为竖直转轴,P 端放在地面上,细绳 AC 和 BC 的结点 C 系一质量为 m 的小球,两绳能承担的最大拉力均为 2.25mg,当 AC 和 BC 均拉直时∠ABC= 90°,∠ACB=53°,细绳 AC 长度为 L=2m,ABC 能绕竖直轴 AP 匀速转动,因而小球在水平面内做匀速圆周运动,当小球的转速增大时,两绳均会被拉断,g 取 10m/s2,
sin 53 0.8 , cos 53 0.6 ,求:
小球线速度为何值时,BC 绳刚好被拉直,并求此时 AC 绳子拉力大小;
若小球的速率继续增加,判断哪条绳先断,并给出理由;求出此时小球的速率。
15.(本题 18 分)如图所示,长度为 L=4m 的长木板置于光滑 水平
地面上,木板右端与固定在水平地面上的半径 R=0.3m 的光滑 的四分之一圆弧轨道平滑连接,M 点为圆弧轨道的最低点。可视为质点的小滑块 A、B 放在长木板的中央,两滑块中间有弹性势能为 E=3.2J 的微型压缩轻弹簧,轻弹簧左端固定在滑块 A 上,右端与滑块 B 接触但不拴接。释放两滑块后,滑块 B 恰好能到达圆弧轨道上与圆心等高的 N 点。已知滑块 A 下表面光滑,滑块 B 与长木板 C 的质量均为 m=0.2kg,二者间的动摩擦因数为μ 0.25 ,重力加速度 g 取 10 m / s2 ,忽略空气阻力的作用。
求 B 到达 M 点时对圆弧轨道的压力大小;
当 A 滑离长木板 C 时,求 B 的速度大小;
若改变两滑块释放的初始位置,使 B 到长木板 C 右端的距离为 kL(0《2024 级高一第二学期期末测试》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B C C A C B AC BD BD
1.D
【详解】当合力的方向与速度方向不在同一条直线上时,物体做曲线运动,曲线运动轨迹特点是:轨迹夹在合力与速度方向之间,合力大致指向轨迹凹的一向.根据该特点知,只有方向 2、3、4 可能.故选 D.
点睛:本题关键是对质点做曲线运动的条件的考查,掌握了做曲线运动的条件,以及曲线运动轨迹的特点,本题基本上就可以解决了.
2.B
【详解】A.卡文迪许首先测量出了万有引力常量数值,A 错误; B.图示引力常量测量实验中运用了放大法,B 正确; C.根据牛顿第三定律,图示实验中的大球对小球引力等于小球对大球引力,C 错误; D.当r 0 时,物体间引力不是无穷大,因为当r 0 时,万有引力定律不成立,D 错误。故选 D。
3.C
【详解】A.第二幅图是网球刚与地面接触时拍摄,之后由于网球受到的弹力仍小于网球的重力,网球继续向下加速运动,当于网球受到的弹力等于网球的重力时,网球的动能最大,故 A 错误; B.网球与地面碰撞整个过程中,由于重力有一定的冲量,根据动量定理可知,弹力的冲量和重力的冲量的矢量和等于网球动量的改变量,故 B 错误; C.网球与地面碰撞过程中,由于忽略空气阻力和网球与地面碰撞的能量损失,则网球的机械能守恒,故 C 正确; D.网球与地面碰撞整个过程中,地面对网球的弹力的作用点没有发生位移,所以地面对网球的弹力不做功,故 D 错误。
故选 C。 4.C
【详解】根据万有引力提供向心力,得G Mm mg
R2
可得星体表面的重力加速度 g GM
R2
Gliese12b 和地球的质量之比约为 4∶1,半径之比约为 1∶1,则 Gliese12b 表面和地球表面的重力加速度大小之比约为 4∶1
又根据h 1 gt 2
2
可得在 Gliese12b 表面和地球表面相同高度做平抛运动的时间之比为 1∶2,根据 x v0t
可得相同初速度时平抛的水平距离之比为 1∶2。故选 C。
5.A
【详解】小球在 P 点脱离轨道时,重力沿半径方向的分力提供向心力,则有
v2
mgcosθ m
R
小球从 A 点运动到 P 点,根据机械能守恒定律有mgR 1 cosθ 1 mv2
2
解得cosθ 2 ,v
3 3
故选 A。 6.C
【详解】A.题图可知 0~3.6s 内运动员静止在蹦床上且mg 500N ,图像6s ~ 6.6s 内,弹
力大于重力,运动员处于超重状态,故 A 错误;
由牛顿第二定律可知,运动员加速度大小am
F mg m
可知弹力 F 最大时加速度最大,结合图像弹力最大 2500N,联立解得a 40m/s2
故 B 错误;
当运动员离开蹦床时 F=0,故 0~8.4s 时间内的 6.8s~8.4s 运动员离开蹦床做竖直上抛运动,共运动 t=1.6s,由竖直上抛规律可知,运动员离开蹦床时与落回到蹦床时速度大小相
等,方向相反,则运动员离开蹦床时速度大小v g t 8m/s
2
规定向上为正方向, 8.4s ~ 9.4s 内,由动量定理得 IF mg t mv m v
其中 t 1.0s
联立解得蹦床给运动员的冲量大小 IF 1300N·s
故 C 正确; D.对运动员和蹦床构成的系统,只有重力与蹦床弹力做功,故系统机械能守恒,即运动 员动能、运动员重力势能、蹦床弹性势能之和不变,图像可知4.8s ~ 5.4s 内,弹力先增大后减小,可知蹦床弹性势能先增大后减小,故运动员重力势能与动能之和先减小后增大,故 D 错误。
故选 C。 7.B
【详解】A.在 B 点绳末端,由关联速度可得,沿绳方向的分速度v1 v cosθ
人向右移动过程中,θ减小,v 不变,故v1 增大,即重物加速上升,A 错误;
人到达 B 点时,由动滑轮特点,物体上升的速度v 1 v
即重物重力的功率 P mgv2 200W
B 正确;
2 2 1
由能量守恒定律,人对重物做的功等于重物机械能的增量,右侧绳长增长
L
h
sinθ
h 2m
重物上升的高度 H 1 L 1m
2
则W mgH 1 mv2 120J
2 2
C 错误;
人行走时,受到的静摩擦力水平向右,人对地面的摩擦力水平向左,D 错误。故选 B。
8.AC
【详解】AB.由题图可知发生事故时,卡车在做圆周运动,从图可以看出卡车冲入民宅时做离心运动,A 正确 B 错误; CD.汽车在水平路面上拐弯时,靠静摩擦力提供向心力,现在易发生侧翻可能是路面设计不合理,公路的设计上可能内侧(东北)高外侧(西南)低,重力沿斜面方向的分力背离圆心,导致合力不够提供向心力而致,故 C 正确,D 错误。
故选 AC。 9.BD
【详解】A.题意知足球两次在空中运动的最大高度 H 相等,根据斜抛运动,竖直方向有
H vOy
2g
可知,足球两次被踢出时的初速度的竖直分量相同,由t 2vOy
g
可知,足球两次在空中运动的时间相同,故 A 错误;
BC.已知ON 3OM ,由 x vOxt
可知,足球第二次被踢出时的初速度的水平分量是第一次的 3 倍,足球被踢出时的初速度大小v
被踢出时的初动能 E 1 mv2 1 m v 2 v 2
k 2 2 Ox Oy
故足球第二次被踢出时的动能不是第一次的 9 倍,故 B 正确、C 错误; D.根据机械能守恒定律和斜抛运动的对称性可知,足球落地时的速度与水平方向的夹角
满足tanθ vOy
vOx
可知tanθM 3tanθN
故 D 正确。故选 BD。 10.BD
【详解】A.由机械能守恒定律 1 mv2 1 mv2 mgh
2 0 2
解得v2 2gh v2
由图乙可知,当h 0.25m 时, v2 4m2 /s2 代入上式,解得v0 3m/s
又当h 0 时,则有v2 v2 9m2 /s2 ,即 x 9
A 错误;
B.由题图乙可知,轨道半径 R 0.125m ,小球在 C 点的速度vC 2m/s
v2
由牛顿第二定律可得 F mg m C
R
解得m 0.5kg
B 正确;
CD.小球从 A 到 B 过程中由机械能守恒有 1 mv2 1 mv2 mgR
2
v2
在 B 点,根据牛顿第二定律可得 NB m B
R
0 2 B
代入数据解得 NB 26N
由于小球还受重力作用,小球在 B 点所受合力为
C 错误,D 正确。故选 BD。
262 52 N 26N
11.
v
M
M m
【详解】(1)[1]由动能定理可知
Mgh 1 Mv2
得
(2)[2]由动能定理可知
2 0
v0
经计算得
μ M m gs 1 M m v2
2
v
(3)[3]A、B 碰撞的过程中动量守恒应满足
12.(1) 0.05 1
(2) 0.240 0.245
2πMg
(3) M 2m d
M
M m
【详解】(1)[1]根据角速度与周期的关系有
[2]根据运动学公式有
T 2π
ω
2π s 0.05s 40π
v xDF 18.00 8.00 10 2 m/ s 1m/ s
1 2T 2 0.05
(2)[1]在 OE 段,系统动能的增加量为
ΔE 1 M 2m v 2 1 0.200 2 0.140 12 J 0.240J
k 2 1 2
[2]重力势能的减少量为
ΔE M m gh mgh 0.200 9.8 12.50 10 2 J 0.245J
p OE OE
从初始时激光笔对准 K 上某点开始选取连续的 n 段,根据时间关系有
` 2nπ 1 kt 2
2
根据运动学公式有
根据机械能守恒定律有
解得
vt nd
2
Mgnd 1 M 2m v2
2
M 2m kd
则
x 2h
2hR2
Mg
k
2π
2πMg
M 2m d
2hR
13.(1) t ;(2) t 2
;(3)
Gt 2
;(4)
t
【详解】(1)小球做平抛运动,在水平方向做匀速直线运动,则有
x v0t
解得
v x
0 t
小球做平抛运动时在竖直方向上做自由落体运动,则有
h 1 gt 2
2
解得该星球表面的重力加速度为
g 2h
t 2
设静止在星球地面上的物体质量为 m,由万有引力等于物体的重力得
G Mm mg R2
解得该星球的质量为
gR2
M
2hR2
G Gt 2
设有一颗质量为 m0 的近地卫星绕星球做匀速圆周运动,速率为 v,由牛顿第二定律得
2
G 0 m0
R2
代入数据解得该星球的第一宇宙速度为
v
R
2hR t
14.(1) v 3m/s , 5 mg ;(2)BC 绳先断,见解析, v 6m/s
1 4 2
【详解】(1)当小球线速度增大时,BC 逐渐被拉直,小球线速度增至 BC 刚被拉直时,对球在竖直方向由平衡条件有
在水平方向由牛顿第二定律有
其中
TA sin ACB mg 0
v2 TA cos ACB TB m 1
r
r BC L cos ACB BC 刚被拉直时TB 0 ,可求得 AC 绳中的拉力
T 5 mg , v 3m/s
A 4 1
(2)由上知线速度再增大些,TA 不变而 TB 增大,所以 BC 绳先断。当 BC 绳刚要断时,拉力为 2.25mg,则代入
v2 TA cos ACB TB m 2
r
解得
v2 6m/s
15.(1)6N
2.75m / s
Wf克 1.2 0.5(k J)
【详解】(1)设 B 在 M 点时的速度大小为v ,则有mgR 1 mv2
M 2 M
v2
设在 M 点时圆弧轨道对 B 的支持力为 FN ,则有 FN mg m M
R
解得 FN 6N
由牛顿第三定律可知,B 运动到 M 点时对圆弧轨道的压力大小为 6N。
设滑块 B 刚被弹开时的速度大小为v ,由动能定理有-μmg L 1 mv2
1 mv2
B 2 2 M 2 B
设 A 的质量为mA ,刚被弹开时的速度大小为vA 由动量守恒定律可得mA vA mvB
由能量守恒定律可得 E 1 m v2 1 mv2
2 A A 2 B
联立解得mA 0.2kg,vA vB 4 m/s
A 离开长木板 C 所用的时间为t1 2v 0.5s
A
由题意可判断这段时间内 B 一直在长木板 C 上运动,设 B 减速运动时的加速度大小为a ,由牛顿第二定律可得μmg ma
A 离开长木板 C 时 B 的速度大小为v' v at 2.75m / s
B B 1
若 B 恰好滑到长木板的右端,则有 μmgkL 0 1 mv2
B
解得 k=0.8
①若 0.8≤k≤1,则 B 一直在长木板 C 上运动,直至速度减为零,故 B 克服摩擦力做的功为
W 1 mv2
f克 2 B
解得Wf克 1.6J
②若0 k 0.8 ,则 B 先滑上圆弧轨道,返回后最后与长木板共速,设滑块 B 运动到长木
板最右端时的速度为v' ,则有μmgkL 1 mv2 1 mv'2
M 2 B 2 M
B 从光滑的圆弧轨道滑到长木板上时,其速度大小仍为v' ,设 B 与 C 共速时的速度大小
为 v,则有mv' 2mv
故整个过程中 B 克服摩擦力做的功为W 1 mv2 1 2mv2
f克 2 B 2
联立解得Wf克 1.2 0.5(k J)
物理科试卷
一、单选题(每题 4 分,共 28 分)
如图所示,曲线 AB 为一质点的运动轨迹,某人在曲线上 P 点做出质点在经过该处时其受力的 8 个可能方向,正确的是
只有方向 2、3、4 可能
只有方向 1、3 可能
只有方向 1、2、3、4、5 可能
D.8 个方向都可能 2.牛顿发现了万有引力定律,并给出了物体间引力大小表达式
F G m1m2 ,但没有给出引力常量 G 的具体取值。如图为人类第一次在实验室测量出万有
r 2
引力常量的实验示意图,通过此套装置比较精确测量出了万有引力常量数值,引力常量的精确测定对深入研究物体之间相互作用规律更有意义。以下说
法正确的是( ) A.图示引力常量测量实验中运用了放大法 B.根据万有引力定律表达式,当 r→0 时,物体间引力将趋于无穷大 C.图示实验中的大球对小球引力大于小球对大球引力 D.伽利略首先测量出了万有引力常量数值
3.下面五幅图是网球竖直下落与地面碰撞后又弹起的过程。 从左往右,第二幅图是网球刚与地面接触时拍摄,第三幅图是网球形变量最大时拍摄,忽略空气阻力和网球与地面碰撞的能量损失。 下列说法正确的是( )
A.拍摄第二幅图时,网球的动能最大 B.网球与地面碰撞整个过程中,弹力的冲量等于网球动量的改变量 C.网球与地面碰撞过程中,地面对网球的弹力不做功 D.网球与地面碰撞整个过程中,地面对网球的弹力先做正功后做负功
4.2024 年科学家发现了一颗距离地球 40 光年的类地行星 Gliese12b,这颗行星的发现引发了全球对“第二颗地球”的热议。Gliese12b 体积和地球差不多,质量约为地球的 4 倍。将某物体分别在 Gliese12b 表面与地球表面水平抛出,若水平抛出的高度和初速度均相同,则物体第一次落地时水平距离之比约为( )
A.4∶1 B.1∶4 C.1∶2 D.2∶1
如图,表面光滑的竖直圆环轨道固定在水平面上,半径为 R ,一小球静止在轨道的最高点 A 点。小球受到轻微的扰动,从 A 点由静止沿轨道滑下,一段时间后,小球在 P 点脱离轨道,速度大小为 v, P、O 两点的连线与竖直方向的夹角为θ,小球可看作质点,重力加速度大小为 g,下列说法正确的是( )
cosθ 2 , v 2 3gR
3
cosθ 2 , v
3
cosθ 1 , v
3
3
6gR 3
6gR 3
cosθ 1 , v 2 3gR
3 3
蹦床是一项运动员利用蹦床的反弹在空中表现杂技技巧的竞技运动。将运动员蹦床比赛时的运动看做竖直方向的直线运动,忽略空气阻力。用力传感器测出蹦床对运动员弹力的大小 F,F 随时间 t 的变化规律如图所示,重力加速度 g 取10m / s2 ,则下列说法正确的是( )
6s ~ 6.6s 内,运动员处于失重状态
运动员的最大加速度大小为50m / s2
4.8s ~ 5.4s 内,运动员重力势能与动能之和先增大后减小
8.4s ~ 9.4s 内,蹦床给运动员的冲量大小为 1300Ns 7.如图所示,细绳一端固定在天花板上,另一端跨过一光滑动滑轮和两固定在天花板上的光滑定滑轮,动滑轮下端挂有一重物。某人抓住绳的一端,从右侧定滑轮正下方 A 点以 v 5m/s 的速度匀速移动到 B 点,此时细绳与水平方向的夹角为θ 37 。已知重物质量为
m 10kg ,右侧定滑轮与 A 点的竖直高度 h 3m ,重力加速度 g 10m/s2 , sin 37° 0.6 ,不考虑滑轮的大小和质量,下列说法正确的是( )
重物处于失重状态
人到达 B 点时,重物重力的功率大小为 200W C.整个过程人对重物做功为 100J D.人行走时,对地面的摩擦力方向水平向右
二、多选题(每题 6 分,共 18 分)
汕头电视台《今日说法》栏目曾报道过一起发生在汕头某路上的离奇交通事故。家住公路拐弯处的张先生和李先生家在三
个月内连续遭遇了七次大卡车侧翻在自家门口的场面,第八次有辆卡车冲撞进李先生家,造成三死一伤和房屋严重损毁的血腥惨案.经公安部门和交通部门协力调查,画出的现场 示意图如图所示。交警根据图示作出以下判断,你认为正确的是( )
由图可知汽车在拐弯时发生侧翻是因为车做离心运动 B.由图可知汽车在拐弯时发生侧翻是因为车做向心运动 C.公路在设计上可能内(东北)高外(西南)低 D.公路在设计上可能外(西南)高内(东北)低
9.2024 年 11 月 23 日,2024 中国足协杯决赛在温州奥体中心举行。如图甲所示,一足球运动员在水平草地上练习传高空球。如果他在同一地点把同一个足球前后两次斜向上踢出,第一次足球落在草地上的M 点,第二次落在草地上的 N 点,足球两次在空中运动的最大 高度相等,且ON 3OM ,空气阻力不计,如图乙所示。下列说法正确的是( )
足球第二次被踢出时的初动能一定是第一次的 9 倍 B.足球两次在空中运动的时间不相同 C.足球两次落地时的速度与水平方向夹角的关系为 tanθM=3tanθN D.足球第二次被踢出时的初速度的水平分量是第一次的 3 倍
如题图甲所示,竖直平面内固定一光滑的半圆形轨道 ABC,B 点为 AC 轨道的中点, 小球以一定的初速度从最低点 A 冲上轨道,小球在半圆形轨道上从 A 运动到 C 的过程中,其速度的平方与对应高度的关系图像如图乙。已知小球在最高点 C 受到轨道的弹力大小为 11N,不计空气阻力,g=10m/s2,则( )
A.图乙中 x 为 9m2 s-2 B.小球质量为0.5kg
C.小球在 A 点所受支持力为 36N D.小球在 B 点所受合力大于 26N
三、实验题(每空 2 分,共 16 分)
某实验小组应用下图装置探究动量守恒定律,光滑斜面与水平面间平滑连接,质量为
M 的小球 A 从斜面上高 h 处滑下,小球 A 与质量为 m 的静止滑块 B 对心碰撞并一起向前运动距离 s 后停下来。A、B 与水平地面间的动摩擦因数均为 μ ,重力加速度为 g。
(1)A 物体到达地面瞬间的速度为 ;
A、B 碰后瞬间的速度为 ;
若 A、B 碰撞的过程中动量守恒,应满足的关系式为 。(应用题目中所给字母进行表示)
某同学用如图(a)所示的装置验证机械能守恒定律。不可伸长的轻绳绕过轻质定滑轮,轻绳两端分别连接物块 P 与感光细钢柱 K,两者质钢柱量均为m 0.140kg ,钢柱 K下端与质量为M 0.200kg 的物块 Q 相连。铁架电动机台下部固定一个电动机,电动机竖直转轴上装一支激光笔,电动机带动激光笔绕转轴在水平面内匀速转动,每转一周激光照
经判断系统由静止释放时激光笔光束恰好经过 O 点。参照图(b),在 OE 段,系统动能的增加量Δ Ek ,重力势能的减少量Δ Ep ;比较两者关系可判断系统机械能是否守恒。(计算结果均保留 3 位有效数字)
选取相同的另一感光细钢柱 K,若初始时激光笔对准 K 上某点,开启电动机的同时系统由静止释放,电动机的角速度按如图(c)所示的规律变化,图像斜率为 k,记录下如图
(d)所示的感光痕迹,其中两相邻感光痕迹间距均为 d。若验证得到表达式 k= 即可证明系统在运动过程中机械能守恒(用含字母 M、m、d、k、g、π 的表达式表示)。
四、计算题(共 38 分)
13.(本题 10 分)一宇航员在某未知星球的表面上做平抛运动实验:在离地面 h 高处让小球以某一初速度水平抛出,他测出小球落地点与抛出点的水平距离为 x 和落地时间 t,又已知该星球的半径为 R,已知万有引力常量为 G,求:
该星球表面的重力加速度 g
该星球的质量 M
该星球的第一宇宙速度 v(最后结果必须用题中已知物理量表示)
14.(本题 10 分)如图所示 AP 为竖直转轴,P 端放在地面上,细绳 AC 和 BC 的结点 C 系一质量为 m 的小球,两绳能承担的最大拉力均为 2.25mg,当 AC 和 BC 均拉直时∠ABC= 90°,∠ACB=53°,细绳 AC 长度为 L=2m,ABC 能绕竖直轴 AP 匀速转动,因而小球在水平面内做匀速圆周运动,当小球的转速增大时,两绳均会被拉断,g 取 10m/s2,
sin 53 0.8 , cos 53 0.6 ,求:
小球线速度为何值时,BC 绳刚好被拉直,并求此时 AC 绳子拉力大小;
若小球的速率继续增加,判断哪条绳先断,并给出理由;求出此时小球的速率。
15.(本题 18 分)如图所示,长度为 L=4m 的长木板置于光滑 水平
地面上,木板右端与固定在水平地面上的半径 R=0.3m 的光滑 的四分之一圆弧轨道平滑连接,M 点为圆弧轨道的最低点。可视为质点的小滑块 A、B 放在长木板的中央,两滑块中间有弹性势能为 E=3.2J 的微型压缩轻弹簧,轻弹簧左端固定在滑块 A 上,右端与滑块 B 接触但不拴接。释放两滑块后,滑块 B 恰好能到达圆弧轨道上与圆心等高的 N 点。已知滑块 A 下表面光滑,滑块 B 与长木板 C 的质量均为 m=0.2kg,二者间的动摩擦因数为μ 0.25 ,重力加速度 g 取 10 m / s2 ,忽略空气阻力的作用。
求 B 到达 M 点时对圆弧轨道的压力大小;
当 A 滑离长木板 C 时,求 B 的速度大小;
若改变两滑块释放的初始位置,使 B 到长木板 C 右端的距离为 kL(0
题号 1 2 3 4 5 6 7 8 9 10
答案 D B C C A C B AC BD BD
1.D
【详解】当合力的方向与速度方向不在同一条直线上时,物体做曲线运动,曲线运动轨迹特点是:轨迹夹在合力与速度方向之间,合力大致指向轨迹凹的一向.根据该特点知,只有方向 2、3、4 可能.故选 D.
点睛:本题关键是对质点做曲线运动的条件的考查,掌握了做曲线运动的条件,以及曲线运动轨迹的特点,本题基本上就可以解决了.
2.B
【详解】A.卡文迪许首先测量出了万有引力常量数值,A 错误; B.图示引力常量测量实验中运用了放大法,B 正确; C.根据牛顿第三定律,图示实验中的大球对小球引力等于小球对大球引力,C 错误; D.当r 0 时,物体间引力不是无穷大,因为当r 0 时,万有引力定律不成立,D 错误。故选 D。
3.C
【详解】A.第二幅图是网球刚与地面接触时拍摄,之后由于网球受到的弹力仍小于网球的重力,网球继续向下加速运动,当于网球受到的弹力等于网球的重力时,网球的动能最大,故 A 错误; B.网球与地面碰撞整个过程中,由于重力有一定的冲量,根据动量定理可知,弹力的冲量和重力的冲量的矢量和等于网球动量的改变量,故 B 错误; C.网球与地面碰撞过程中,由于忽略空气阻力和网球与地面碰撞的能量损失,则网球的机械能守恒,故 C 正确; D.网球与地面碰撞整个过程中,地面对网球的弹力的作用点没有发生位移,所以地面对网球的弹力不做功,故 D 错误。
故选 C。 4.C
【详解】根据万有引力提供向心力,得G Mm mg
R2
可得星体表面的重力加速度 g GM
R2
Gliese12b 和地球的质量之比约为 4∶1,半径之比约为 1∶1,则 Gliese12b 表面和地球表面的重力加速度大小之比约为 4∶1
又根据h 1 gt 2
2
可得在 Gliese12b 表面和地球表面相同高度做平抛运动的时间之比为 1∶2,根据 x v0t
可得相同初速度时平抛的水平距离之比为 1∶2。故选 C。
5.A
【详解】小球在 P 点脱离轨道时,重力沿半径方向的分力提供向心力,则有
v2
mgcosθ m
R
小球从 A 点运动到 P 点,根据机械能守恒定律有mgR 1 cosθ 1 mv2
2
解得cosθ 2 ,v
3 3
故选 A。 6.C
【详解】A.题图可知 0~3.6s 内运动员静止在蹦床上且mg 500N ,图像6s ~ 6.6s 内,弹
力大于重力,运动员处于超重状态,故 A 错误;
由牛顿第二定律可知,运动员加速度大小am
F mg m
可知弹力 F 最大时加速度最大,结合图像弹力最大 2500N,联立解得a 40m/s2
故 B 错误;
当运动员离开蹦床时 F=0,故 0~8.4s 时间内的 6.8s~8.4s 运动员离开蹦床做竖直上抛运动,共运动 t=1.6s,由竖直上抛规律可知,运动员离开蹦床时与落回到蹦床时速度大小相
等,方向相反,则运动员离开蹦床时速度大小v g t 8m/s
2
规定向上为正方向, 8.4s ~ 9.4s 内,由动量定理得 IF mg t mv m v
其中 t 1.0s
联立解得蹦床给运动员的冲量大小 IF 1300N·s
故 C 正确; D.对运动员和蹦床构成的系统,只有重力与蹦床弹力做功,故系统机械能守恒,即运动 员动能、运动员重力势能、蹦床弹性势能之和不变,图像可知4.8s ~ 5.4s 内,弹力先增大后减小,可知蹦床弹性势能先增大后减小,故运动员重力势能与动能之和先减小后增大,故 D 错误。
故选 C。 7.B
【详解】A.在 B 点绳末端,由关联速度可得,沿绳方向的分速度v1 v cosθ
人向右移动过程中,θ减小,v 不变,故v1 增大,即重物加速上升,A 错误;
人到达 B 点时,由动滑轮特点,物体上升的速度v 1 v
即重物重力的功率 P mgv2 200W
B 正确;
2 2 1
由能量守恒定律,人对重物做的功等于重物机械能的增量,右侧绳长增长
L
h
sinθ
h 2m
重物上升的高度 H 1 L 1m
2
则W mgH 1 mv2 120J
2 2
C 错误;
人行走时,受到的静摩擦力水平向右,人对地面的摩擦力水平向左,D 错误。故选 B。
8.AC
【详解】AB.由题图可知发生事故时,卡车在做圆周运动,从图可以看出卡车冲入民宅时做离心运动,A 正确 B 错误; CD.汽车在水平路面上拐弯时,靠静摩擦力提供向心力,现在易发生侧翻可能是路面设计不合理,公路的设计上可能内侧(东北)高外侧(西南)低,重力沿斜面方向的分力背离圆心,导致合力不够提供向心力而致,故 C 正确,D 错误。
故选 AC。 9.BD
【详解】A.题意知足球两次在空中运动的最大高度 H 相等,根据斜抛运动,竖直方向有
H vOy
2g
可知,足球两次被踢出时的初速度的竖直分量相同,由t 2vOy
g
可知,足球两次在空中运动的时间相同,故 A 错误;
BC.已知ON 3OM ,由 x vOxt
可知,足球第二次被踢出时的初速度的水平分量是第一次的 3 倍,足球被踢出时的初速度大小v
被踢出时的初动能 E 1 mv2 1 m v 2 v 2
k 2 2 Ox Oy
故足球第二次被踢出时的动能不是第一次的 9 倍,故 B 正确、C 错误; D.根据机械能守恒定律和斜抛运动的对称性可知,足球落地时的速度与水平方向的夹角
满足tanθ vOy
vOx
可知tanθM 3tanθN
故 D 正确。故选 BD。 10.BD
【详解】A.由机械能守恒定律 1 mv2 1 mv2 mgh
2 0 2
解得v2 2gh v2
由图乙可知,当h 0.25m 时, v2 4m2 /s2 代入上式,解得v0 3m/s
又当h 0 时,则有v2 v2 9m2 /s2 ,即 x 9
A 错误;
B.由题图乙可知,轨道半径 R 0.125m ,小球在 C 点的速度vC 2m/s
v2
由牛顿第二定律可得 F mg m C
R
解得m 0.5kg
B 正确;
CD.小球从 A 到 B 过程中由机械能守恒有 1 mv2 1 mv2 mgR
2
v2
在 B 点,根据牛顿第二定律可得 NB m B
R
0 2 B
代入数据解得 NB 26N
由于小球还受重力作用,小球在 B 点所受合力为
C 错误,D 正确。故选 BD。
262 52 N 26N
11.
v
M
M m
【详解】(1)[1]由动能定理可知
Mgh 1 Mv2
得
(2)[2]由动能定理可知
2 0
v0
经计算得
μ M m gs 1 M m v2
2
v
(3)[3]A、B 碰撞的过程中动量守恒应满足
12.(1) 0.05 1
(2) 0.240 0.245
2πMg
(3) M 2m d
M
M m
【详解】(1)[1]根据角速度与周期的关系有
[2]根据运动学公式有
T 2π
ω
2π s 0.05s 40π
v xDF 18.00 8.00 10 2 m/ s 1m/ s
1 2T 2 0.05
(2)[1]在 OE 段,系统动能的增加量为
ΔE 1 M 2m v 2 1 0.200 2 0.140 12 J 0.240J
k 2 1 2
[2]重力势能的减少量为
ΔE M m gh mgh 0.200 9.8 12.50 10 2 J 0.245J
p OE OE
从初始时激光笔对准 K 上某点开始选取连续的 n 段,根据时间关系有
` 2nπ 1 kt 2
2
根据运动学公式有
根据机械能守恒定律有
解得
vt nd
2
Mgnd 1 M 2m v2
2
M 2m kd
则
x 2h
2hR2
Mg
k
2π
2πMg
M 2m d
2hR
13.(1) t ;(2) t 2
;(3)
Gt 2
;(4)
t
【详解】(1)小球做平抛运动,在水平方向做匀速直线运动,则有
x v0t
解得
v x
0 t
小球做平抛运动时在竖直方向上做自由落体运动,则有
h 1 gt 2
2
解得该星球表面的重力加速度为
g 2h
t 2
设静止在星球地面上的物体质量为 m,由万有引力等于物体的重力得
G Mm mg R2
解得该星球的质量为
gR2
M
2hR2
G Gt 2
设有一颗质量为 m0 的近地卫星绕星球做匀速圆周运动,速率为 v,由牛顿第二定律得
2
G 0 m0
R2
代入数据解得该星球的第一宇宙速度为
v
R
2hR t
14.(1) v 3m/s , 5 mg ;(2)BC 绳先断,见解析, v 6m/s
1 4 2
【详解】(1)当小球线速度增大时,BC 逐渐被拉直,小球线速度增至 BC 刚被拉直时,对球在竖直方向由平衡条件有
在水平方向由牛顿第二定律有
其中
TA sin ACB mg 0
v2 TA cos ACB TB m 1
r
r BC L cos ACB BC 刚被拉直时TB 0 ,可求得 AC 绳中的拉力
T 5 mg , v 3m/s
A 4 1
(2)由上知线速度再增大些,TA 不变而 TB 增大,所以 BC 绳先断。当 BC 绳刚要断时,拉力为 2.25mg,则代入
v2 TA cos ACB TB m 2
r
解得
v2 6m/s
15.(1)6N
2.75m / s
Wf克 1.2 0.5(k J)
【详解】(1)设 B 在 M 点时的速度大小为v ,则有mgR 1 mv2
M 2 M
v2
设在 M 点时圆弧轨道对 B 的支持力为 FN ,则有 FN mg m M
R
解得 FN 6N
由牛顿第三定律可知,B 运动到 M 点时对圆弧轨道的压力大小为 6N。
设滑块 B 刚被弹开时的速度大小为v ,由动能定理有-μmg L 1 mv2
1 mv2
B 2 2 M 2 B
设 A 的质量为mA ,刚被弹开时的速度大小为vA 由动量守恒定律可得mA vA mvB
由能量守恒定律可得 E 1 m v2 1 mv2
2 A A 2 B
联立解得mA 0.2kg,vA vB 4 m/s
A 离开长木板 C 所用的时间为t1 2v 0.5s
A
由题意可判断这段时间内 B 一直在长木板 C 上运动,设 B 减速运动时的加速度大小为a ,由牛顿第二定律可得μmg ma
A 离开长木板 C 时 B 的速度大小为v' v at 2.75m / s
B B 1
若 B 恰好滑到长木板的右端,则有 μmgkL 0 1 mv2
B
解得 k=0.8
①若 0.8≤k≤1,则 B 一直在长木板 C 上运动,直至速度减为零,故 B 克服摩擦力做的功为
W 1 mv2
f克 2 B
解得Wf克 1.6J
②若0 k 0.8 ,则 B 先滑上圆弧轨道,返回后最后与长木板共速,设滑块 B 运动到长木
板最右端时的速度为v' ,则有μmgkL 1 mv2 1 mv'2
M 2 B 2 M
B 从光滑的圆弧轨道滑到长木板上时,其速度大小仍为v' ,设 B 与 C 共速时的速度大小
为 v,则有mv' 2mv
故整个过程中 B 克服摩擦力做的功为W 1 mv2 1 2mv2
f克 2 B 2
联立解得Wf克 1.2 0.5(k J)
同课章节目录
