2.2 机械波的图像描述 教案

波动图象专题
波动图象是高考命题频率最多的知识点，题型主要以选择和填空题居多，偶尔也有计算题型．波的图象是高考的重点也是高考的难点．
波的图象要与振动图象区别开．简谐运动的图象，反映的是质点相对平衡位置的位移随时间变化的规律，图线随着时间的继续要延伸，但原有图形不变．波动图象，反映的是同一时刻介质中各个质点相对各自平衡位置的位移，波形在不同时刻呈现不同，但波形具有周期性和重复性．
波的周期性分空间周期性(在同一波线上，相距为波长整数倍的各个质点的振动情况完全相同)和时间周期性(波在传播过程中，经过整数倍周期时，其波形图线相同)．
波的图象问题要注意以下五种情况可能引起的多解：
⑴波的空间周期性引起；
⑵波的时向周期性引起；
⑶波的双向性引起；
⑷介质两质点间距离与波长关系未定引起；
⑸介质质点振动方向未定引起．
解波的图象问题的方法：
⑴波形平移法(△t后的波形，由原波形沿波传播方向平移．而得)；
⑵波图象定义法 (寻找某时刻各介质质点的位移矢量，连各矢量末端而成)；
⑶振动落后法(离振源越远的质点振动越落后)；
⑷“上下坡”法(波形上坡段质点向下运动，波形下坡段质点向上运动)．

【典型例题透析】

㈠识图类
〖例1〗一列横波在t=0时刻的波形如图中实线所示，在t=1s时刻的波形如图中虚线所示．由此可以判定此波的：
A.波长一定是4cm B.周期一定是4s
C.振幅一定是2cm D.传播速度一定是1 cm/s
〖命题意图〗
考查波长、周期、振幅和传播速度概念，考查公式和波的双向性，考查从图中搜取信息的能力．
〖解题思路〗
由图象可直接得出该波的波长，振幅为2cm，故A、C正确．
但本题中未说明波的传播方向，如波沿x轴正向传播，传播时间，又，；波速．
如波沿x轴负向传播，传播时间，
又，波速．
由以上分析可看出，波速和周期都不是定值．故B、D不对．本题正确答案为AC
〖探讨评价〗
在给定两时刻波形时，若不告之波的传播方向，要注意波的双向性可能引起的多解．
㈡绘图类试题
绘图类试题分画波形类题和应用波形类题．
1.画波形图
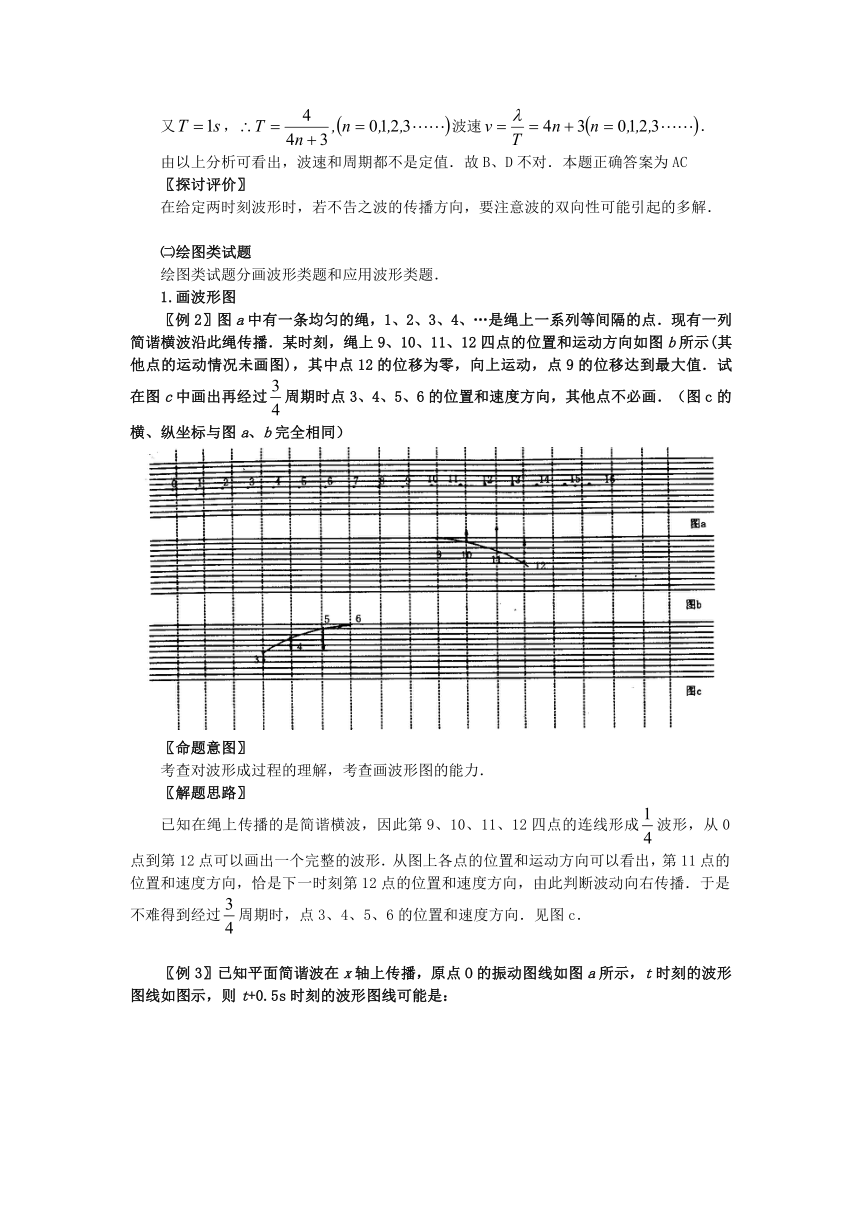
〖例2〗图a中有一条均匀的绳，1、2、3、4、…是绳上一系列等间隔的点．现有一列简谐横波沿此绳传播．某时刻，绳上9、10、11、12四点的位置和运动方向如图b所示(其他点的运动情况未画图)，其中点12的位移为零，向上运动，点9的位移达到最大值．试在图c中画出再经过周期时点3、4、5、6的位置和速度方向，其他点不必画．（图c的横、纵坐标与图a、b完全相同）
〖命题意图〗
考查对波形成过程的理解，考查画波形图的能力．
〖解题思路〗
已知在绳上传播的是简谐横波，因此第9、10、11、12四点的连线形成波形，从0点到第12点可以画出一个完整的波形．从图上各点的位置和运动方向可以看出，第11点的位置和速度方向，恰是下一时刻第12点的位置和速度方向，由此判断波动向右传播．于是不难得到经过周期时，点3、4、5、6的位置和速度方向．见图c．
〖例3〗已知平面简谐波在x轴上传播，原点O的振动图线如图a所示，t时刻的波形图线如图示，则t+0.5s时刻的波形图线可能是：
〖命题意图〗
考查由某一时刻波形画另一时刻波形的能力，考查挖掘图中隐含条件的能力．
〖解题思路〗
由振动图象a可知振动周期T=0.4s，经，即经过个周期后，波动图象与经后的波动图象相同，若波沿x正向传播，则波形b向右平移个波长如图D所示；若波沿x负方向传播，则波形b向左平移个波长如图C所示．选项CD正确．
〖探讨评价〗
由某一时刻波形画另一时刻波形有两种方法：
一是平移法；
二是波的定义法．
一般前一种方法比后一种方法简便．
2.应用波形图
〖例4〗简谐横波某时刻的波形图线如图所示．由此图可知：
A.若质点a向下运动，则波是从左向右传播的
B.若质点b向上运动，则波是从左向右传播的
C.若波从右向左传播，则质点c向下运动
D.若波从右向左传播，则质点d向上运动
〖解题思路〗
利用“上下坡法则”判断
上下坡法则：把波动图线类比凸凹的路面，凸凹路面就有上坡段和下坡段，沿着波的传播方向看去，位于上坡段上的质点就向下运动，下坡段上的质点就向上运动；向上运动的质点位于下坡段，向下运动的质点位于上坡段．
若质点a向下运动，由上下坡法则，a点必位于上坡段，只有由右向左看，a才处于上坡段，故波应向左传，选项A错．同理分析B选项对．
若波从右向左传，由上下坡法则，知d、c点位于下坡段，都应向上运动，故选项C错，D对．正确选项为BD．
〖例5〗一根张紧的水平弹性绳上a、b两点相距14.0m，b点在a点右方，当一列简谐横波沿此绳向右传播时，若a点的位移达到正极大时，b点位移恰好为零且向下运动．经过1.00s后，a点位移为零向下运动，而b点位移恰好达到负极大，则这列简谐波的波速可能等于：
A.4.67m/s B.6m/s C.10m/s D.14m/s
〖命题意图〗
根据波中两质点运动情况求波速．
〖解题思路〗
根据题意可以画出下图，图中实线表示开始时刻的波动图线，虚线表示1.00s以后的波动图线．由图可知：
，即：；
，即：．
又。
容易看出：当时，，当时，．因而找到A、C是正确的，但B、D是否 正确就难以判断．由于n、k是彼此独立的自然数，v值并不单纯随n增大而增大，因可以选较大的k，使v值反而减小，v也不单纯随k的增大而减小，因可以选较大的n，使v反而增加．因此用试选k、n的值来判断这两个答案是否正确是困难的．
我们可以换一种方法：为判断答案B是否正确，可以令v=6m/s，看k、n有无自然数的解：…………①
由①式可得．由于n、k皆为整数，此等式左侧为偶数，不能等于1，所以①式不能成立，可以否定答案B．
同理若，则得出=1，由于2(n-k)为偶数，不能等于1，从而否定了答案D．正确答案只有选项A、C．
〖探讨评价〗
⑴本题未给波的图象，但在解题中设定了一波形，然后就根据这一波形，寻找符合要求的a、b两点，进而找到隐含条件：a、b间距离与波长的关系；时间与周期的关系．如果不借助这一波形，凭想象就很难找到这两个隐含条件，因此，要善于借助图象分析和解决问题．
⑵本题用到了空间周期性和波的时间周期性，