12.2.1全等三角形的判定条件 课件(共40张PPT)
文档属性
| 名称 | 12.2.1全等三角形的判定条件 课件(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 00:00:00 | ||
图片预览









文档简介
(共40张PPT)
12.2.1全等三角形的判定条件
第12章 全等三角形
【2025新教材】华东师大版数学 八年级上册
授课教师:********
班 级:********
时 间:********
全等三角形的判定条件教案
一、教学目标
知识与技能目标:学生能够准确阐述全等三角形的判定条件,包括 “边边边”(SSS)、“边角边”(SAS)、“角边角”(ASA)、“角角边”(AAS)和 “斜边、直角边”(HL,适用于直角三角形);熟练运用这些判定条件判断两个三角形是否全等,能够在具体图形中准确找出对应边和对应角,并依据判定条件进行推理证明;学会利用全等三角形的判定条件解决实际问题,如测量不可直接到达的距离等。
过程与方法目标:通过动手操作、观察、猜想、验证等活动,引导学生经历全等三角形判定条件的探究过程,培养学生的自主探究能力和逻辑推理能力;在运用判定条件解决问题的过程中,提高学生的分析问题、解决问题的能力,让学生体会分类讨论、转化等数学思想方法。
情感态度与价值观目标:激发学生对几何知识的学习兴趣,感受数学与生活的紧密联系;在探究活动中,培养学生勇于探索、敢于质疑的精神,增强学生学习数学的自信心;通过小组合作学习,培养学生的团队协作意识和交流表达能力。
二、教学重难点
教学重点:深入理解并熟练掌握全等三角形的判定条件,能够准确运用这些条件判定两个三角形是否全等;掌握判定条件在不同几何图形和实际问题中的应用方法,这是全等三角形知识的核心,也是后续学习相似三角形、四边形等几何知识的重要基础。
教学难点:在复杂的图形中准确识别对应边和对应角,避免因对应关系错误导致判定失误;理解判定条件的适用范围和限制条件,如 “边边角”(SSA)和 “角角角”(AAA)不能判定两个三角形全等的原因;在实际问题中,能够将问题转化为全等三角形的判定问题,并选择合适的判定条件进行求解,这对学生的空间想象能力和综合运用能力要求较高。
三、教学方法
讲授法:系统讲解全等三角形判定条件的概念、内容和应用要点,确保学生理解核心知识和关键内容。
实验探究法:组织学生进行动手操作实验,如用小棒拼三角形、用纸张裁剪三角形等,通过实验探究全等三角形的判定条件,培养学生的自主探究能力和实践操作能力。
范例教学法:通过典型的例题和练习题,展示全等三角形判定条件的应用技巧和解题思路,让学生掌握正确的解题步骤和书写规范。
小组合作学习法:组织学生开展小组合作学习活动,共同探讨全等三角形判定中的疑难问题,交流学习经验和方法,培养学生的团队协作能力和交流表达能力。
多媒体辅助教学法:利用多媒体课件展示几何图形的动态变化,帮助学生更直观地理解全等三角形的判定条件,增强教学的直观性和趣味性。
四、教学过程
(一)复习导入(5 分钟)
回顾全等三角形概念:提问学生全等三角形的定义,即能够完全重合的两个三角形叫做全等三角形,引导学生回顾全等三角形的对应边相等、对应角相等的性质。
引发思考:教师提出问题:“在实际问题中,我们很难通过将两个三角形重合来判断它们是否全等,那么是否有更简便的方法呢?今天我们就来探究全等三角形的判定条件。” 由此导入本节课的课题。
(二)新课讲授
“边边边”(SSS)判定条件的探究(15 分钟)
实验操作:给每个小组发放三根长度固定的小棒(如 3cm、4cm、5cm),让学生用小棒拼出三角形。引导学生观察发现,无论怎样拼接,得到的三角形形状和大小都相同。
猜想归纳:组织学生进行小组讨论,根据实验现象猜想:三边对应相等的两个三角形全等。
验证证明:教师通过多媒体课件展示两个三边对应相等的三角形,利用平移、旋转、翻折等操作,证明这两个三角形能够完全重合,从而得出 “边边边” 判定条件:三边对应相等的两个三角形全等,可以简写成 “边边边” 或 “SSS”。
应用讲解:以一个简单的几何图形为例,如已知在△ABC 和△DEF 中,AB = DE = 3cm,BC = EF = 4cm,AC = DF = 5cm,讲解如何运用 “SSS” 判定条件证明△ABC≌△DEF,强调书写证明过程的规范格式。
“边角边”(SAS)判定条件的探究(15 分钟)
实验操作:让学生在纸上画出一个三角形,使其中两条边的长度分别为 3cm 和 4cm,这两条边的夹角为 60°。然后小组内成员互相比较所画的三角形,观察发现这些三角形形状和大小相同。
猜想归纳:引导学生猜想:两边和它们的夹角对应相等的两个三角形全等。
验证证明:教师利用几何画板软件,动态展示两个满足 “两边和它们的夹角对应相等” 条件的三角形,通过图形变换证明这两个三角形全等,得出 “边角边” 判定条件:两边和它们的夹角对应相等的两个三角形全等,可以简写成 “边角边” 或 “SAS”。同时强调 “夹角” 的重要性,通过反例说明 “边边角”(SSA)不能判定两个三角形全等。
应用讲解:给出例题,如在△ABC 和△DEF 中,AB = DE = 3cm,∠B = ∠E = 60°,BC = EF = 4cm,讲解如何运用 “SAS” 判定条件证明△ABC≌△DEF,规范证明过程的书写。
“角边角”(ASA)和 “角角边”(AAS)判定条件的探究(20 分钟)
“角边角”(ASA)探究:先让学生思考:如果已知两个三角形的两个角及其夹边对应相等,这两个三角形是否全等?然后通过画三角形的方式进行验证,例如画一个三角形,使两个角分别为 30° 和 60°,它们的夹边为 5cm,小组内比较所画三角形,得出猜想。教师通过几何证明,得出 “角边角” 判定条件:两角和它们的夹边对应相等的两个三角形全等,可以简写成 “角边角” 或 “ASA”。
“角角边”(AAS)探究:引导学生思考:如果两个角和其中一个角的对边对应相等,能否判定两个三角形全等?利用三角形内角和定理,将 “角角边” 的情况转化为 “角边角” 的情况进行证明,从而得出 “角角边” 判定条件:两角和其中一个角的对边对应相等的两个三角形全等,可以简写成 “角角边” 或 “AAS”。
应用讲解:通过多个例题,如在△ABC 和△DEF 中,∠A = ∠D = 30°,∠B = ∠E = 60°,AB = DE = 5cm(ASA 判定);在△ABC 和△DEF 中,∠A = ∠D = 30°,∠C = ∠F = 90°,BC = EF = 4cm(AAS 判定),讲解如何运用这两个判定条件进行证明,强化学生对判定条件的理解和应用能力。
“斜边、直角边”(HL)判定条件的探究(10 分钟)
情境引入:教师提出问题:对于两个直角三角形,除了前面的判定条件,是否有特殊的判定方法呢?引导学生思考。
探究证明:让学生画出两个直角三角形,使它们的斜边和一条直角边分别相等,然后通过测量、叠合等方式进行验证。教师再通过几何推理证明,得出 “斜边、直角边” 判定条件:斜边和一条直角边对应相等的两个直角三角形全等,可以简写成 “斜边、直角边” 或 “HL”。强调该判定条件只适用于直角三角形。
应用讲解:给出直角三角形全等判定的例题,如在 Rt△ABC 和 Rt△DEF 中,∠C = ∠F = 90°,AB = DE = 5cm,AC = DF = 3cm,讲解如何运用 “HL” 判定条件证明 Rt△ABC≌Rt△DEF。
(三)课堂练习(15 分钟)
如图,已知 AB = AD,CB = CD,求证:△ABC≌△ADC。
如图,AB = AC,AD = AE,∠BAC = ∠DAE,求证:△ABD≌△ACE。
如图,已知∠A = ∠D,∠B = ∠E,BC = EF,求证:△ABC≌△DEF。
如图,在 Rt△ABC 和 Rt△DEF 中,∠C = ∠F = 90°,AC = DF,AB = DE,求证:Rt△ABC≌Rt△DEF。
让学生独立完成练习,教师巡视课堂,及时发现学生存在的问题,进行个别辅导和集中讲解。针对学生在判定条件应用、对应关系确定、证明过程书写等方面出现的错误进行重点分析,帮助学生掌握正确的解题思路和方法。
(四)课堂小结(5 分钟)
请学生回顾本节课所学内容,分享自己对全等三角形判定条件的理解和收获,以及在学习过程中遇到的困难和解决方法。
教师进行系统总结:强调整体回顾全等三角形的判定条件,包括 “SSS”“SAS”“ASA”“AAS” 和 “HL”,明确每个判定条件的内容、适用范围和注意事项;总结在运用判定条件进行证明时的要点,如准确找出对应边和对应角、规范书写证明过程等;鼓励学生在课后继续加强练习,熟练掌握全等三角形的判定条件,提高几何推理能力。
(五)作业布置(1 分钟)
必做题:课本习题 [对应章节] 第 1 - 5 题,帮助学生巩固全等三角形判定条件的基础知识和基本技能。
选做题:在实际生活中寻找一个可以用全等三角形判定条件解决的问题,并尝试进行解答,如测量池塘两端的距离等,让学生将所学知识应用到实际生活中,提高知识应用能力。
这份教案围绕全等三角形判定条件设计教学环节。你若对教学情境、探究活动、练习难度等方面有新想法,欢迎提出,我们可进一步优化完善。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1、理解并掌握全等三角形的概念,及全等三角形经过一系列变换后,能够完全重合的性质;
2、掌握全等三角形的性质(对应边相等,对应角相等)和全等的判定条件;
下图中的几组图形有怎样的关系?
(1)
(2)
(3)
思考:你能想到现实生活中有这样的图形吗?
能够完全重合的两个图形叫做全等图形.
全等形包括规则图形和不规则图形全等.
全等图形:
知识点一 全等三角形的概念
全等三角形
能够完全重合的两个三角形是全等三角形.
A
B
C
A′
B′
C′
能相互重合的顶点是对应顶点.
能相互重合的边是对应边.
能相互重合的角是对应角.
A与A′、B与B′、C与C′
AB与A′B′、BC与B′C′ 、CA与C′A′
∠A与∠A′、∠B与∠B′、∠C与∠C′
A
B
C
A′
B′
C′
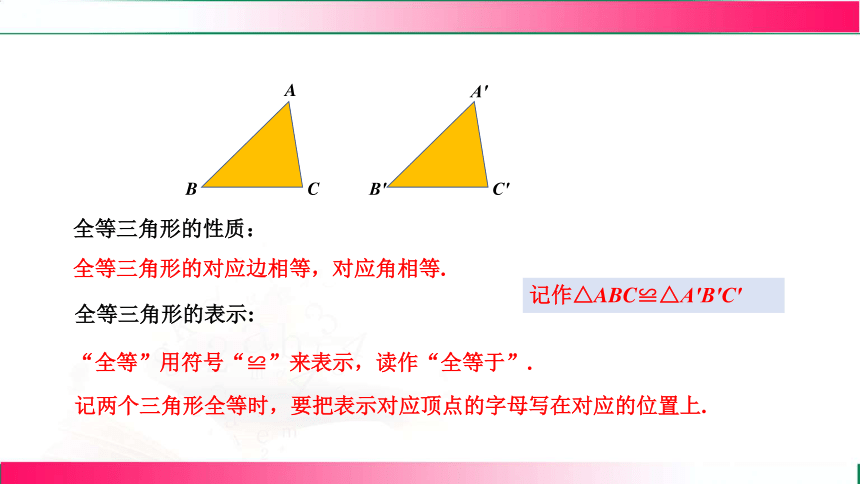
全等三角形的性质:
全等三角形的对应边相等,对应角相等.
全等三角形的表示:
“全等”用符号“≌”来表示,读作“全等于”.
记两个三角形全等时,要把表示对应顶点的字母写在对应的位置上.
记作△ABC≌△A′B′C′
1.怎样改变其中一个图形的位置可以得到另一个图形?
观察与思考
2.你能在以下图案中能找出全等图形吗?
做
一
做
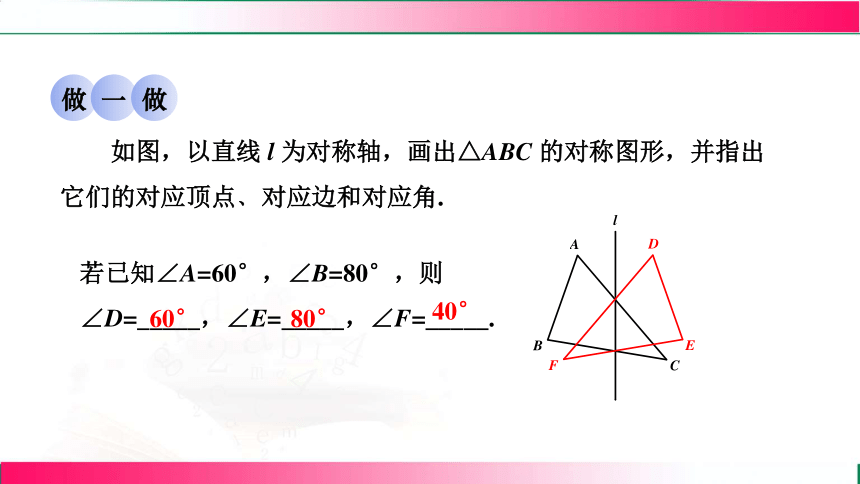
如图,以直线 l 为对称轴,画出△ABC 的对称图形,并指出它们的对应顶点﹑对应边和对应角.
若已知∠A=60°,∠B=80°,则
∠D=_____,∠E=_____,∠F=_____.
60°
80°
40°
典例精析
【例1】 如图,将△ABC 绕点 B 按顺时针方向旋转 60°后得△A′BC′.指出对应顶点、对应边和对应角.
解: 对应顶点: A 与A′,B 与B,C 与 C′;
对应边: AB 与 A′B,AC 与 A′C′,BC 与 BC′.
对应角:∠CBA 与∠C′BA′,∠A 与∠A′,
∠C 与∠C′.
练一练
【解析】∵ △ABC ≌ △DEF,
∴ ∠ACB = ∠DFE.
∴∠DFE = 180°-(∠A +∠B)=85°.
1. 如图,已知△ABC ≌△DEF,∠A =40°, ∠B =55°,则∠DFE 的度数是________.
85°
知识点二 全等三角形的判定条件
怎么判断两个三角形全等呢?
根据全等三角形的定义可知:能够完全重合两个三角形全等,即两个三角形的三对边、三对角分别对应相等,则两个三角形全等.
能否减少一些条件,找到更简便的判定两个三角形全等的方法呢?
对两个三角形来说,六个元素(三条边、三对角)中至少要有几个元素对应相等,这两个三角形才会全等呢?
1.画几个有一边长为8cm的三角形,这样得到的三角形是否全等?
如果两个三角形只有一组对应相等的元素,那么会出现几种情况?这两个三角形会全等吗?
探究活动1
两种,一条边或一个角相等.
试一试
有一条边对应相等的三角形不一定全等.
有一个角对应相等的三角形不一定全等.
2.画几个有一个角为60°的三角形,这样得到的三角形是否全等?
(
60°
归纳:如果两个三角形只有一组对应相等的元素,那么这两个三角形不一定全等.
30°
(1)三角形的一条边为3cm,一个内角为30°
3cm
3cm
3cm
30°
30°
探究活动2
如果两个三角形有两组对应相等的元素,那么会出现几种可能的情况?这两个三角形会全等吗?
三种,一条边和一个角相等;两个角相等;两条边相等.
试一试
按照下面的条件,用刻度尺和量角器画三角形,并和周围的同学比较,所画的图形是否全等.
一条边和一个内角相等不能判定两个三角形全等.
(
(
(
30°
70°
30°
70°
30°
70°
(2)三角形的两个内角分别为30°和70°.
两个内角对应相等不能判定两个三角形全等.
5cm
3cm
3cm
(3)三角形的两条边分别为3cm和5cm.
两条边对应相等不能判定两个三角形全等.
两个三角形只有一组或两组对应相等的元素(边或角),那么这两个三角形不一定全等.
探索发现
思 考
如果两个三角形有三组对应相等的元素(边或角),又会如何呢?
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,最小的边是对应边
(长对长,短对短,中对中);
(5)两个全等三角形最大的角是对应角,最小的角是对应角
(大角对大角,小角对小角);
找对应边、对应角的方法总结:
典例精析
例2 如图,△ABC≌△DEF,∠A=60°,∠E=40°,BF=3,EF=6,求∠DFE的度数和CF的长.
E
D
B
F
A
C
3
60°
40°
6
解:∵△ABC≌△DEF,∠A=60°,
∠E=40°,BF=3,EF=6,
∴∠D=∠A=60°,BC=EF=6,
∴∠DFE=180°-∠E-∠D
=180°-40°-60°
=80°
CF=BC-BF=6-3=3.
练一练
如图,将△AOB 绕点 O 旋转180°,得到△COD,这时△AOB≌△_____. 这两个三角形的对应边是:AO与______,OB与_______,BA与_______;
对应角是:∠AOB与_______,∠OBA与______,
∠BAO与________.
COD
CO
OD
DC
∠COD
∠ODC
∠DCO
2. 如图,AD // BC,AD = BC,AE⊥BC,将△ABE 沿 AD 方向平移,使点 A 与点 D 重合,点 E 平移至点 F, 则△ABE≌______,∠F =_____°.
△DCF
90
1.如图,△ABC ≌△ CED, ∠ B和∠ DEC是对应角,BC与ED是对应边,说出另两组对应角和对应边.
A
B
C
E
D
解: 对应角: ∠ A= ∠ DCE, ∠ D= ∠ ACB;
对应边: AC=CD,AB=CE.
2.下列各组中是全等图形的是( )
A. 两个周长相等的等腰三角形
B. 两个面积相等的长方形
C.两条长度的圆弧
D. 两个周长相等的圆
D
解:周长相等,圆的半径也相等,故两个周长相等的圆全等;
1. 下列说法正确的是( )
B
A. 三个角对应相等的两个三角形全等
B. 判定两个三角形全等的条件中至少有一个条件是边相等
C. 面积相等的两个三角形全等
D. 周长相等的两个三角形全等
返回
2. [2025泰安期末]根据下列已知条件,能画出唯一的
的是( )
C
A. ,
B. ,,
C. , ,
D. ,,
返回
3. 如图,把以点 为旋转中心逆时
针旋转得到,点, 的对应点分
别是点,,且点在 的延长线上,
连结 ,则下列结论一定正确的是( )
A
A. B.
C. D.
返回
(第4题)
4. 如图,将折叠,使点与 边的
中点重合,折痕为.若 ,
,则 的周长为( )
A
A. 12 B. 13 C. 14 D. 15
返回
(第5题)
5.[2025重庆校级期末]两个全等
的直角三角形重叠在一起,将其中
的一个三角形沿着 方向平移到
的位置,, ,
平移距离为2,则阴影部分面积为
___.
7
(第5题)
【点拨】由平移的性质知
, ,
,
,
.
返回
6.如图,将绕点顺时针旋转 得
到, .
(1)和 是否全等?如果全等,
请写出对应边和对应角.
【解】 .
对应边:和,和,和 ;
对应角:和,和, 和
.
(2)直线与直线 有怎样的位置关系?请说明理由.
.
理由:延长交 于点
,
, ,
,
即点,, 在同一直线上.
, ,
, ,
.
返回
7. 图中的小正方形边长都相等,若
,则点 可能是图中的
( )
D
A. 点 B. 点 C. 点 D. 点
返回
8. 一个三角形三条边的长分别是5,7,10,
另一个三角形三条边的长分别是, ,5.若这两个
三角形全等,则 的值为( )
D
A. 7 B. C. 8 D. 或7
【点拨】分两种情况讨论: 解得
;解得
.综上所述,的值是 或7.
返回
9.[2025武汉月考]如图①,数轴上从左至右依次有, ,
,,五个点,其中点,,表示的数分别为 ,0,
4.如图②,将数轴在点的左侧部分绕点 顺时针方向旋转
,将数轴在点的右侧部分绕点逆时针方向旋转 ,
连结,.若和全等,则点 表示的数为
_______________.
或
全等三角形
定义
性质
1.全等三角形的对应边相等
2.全等三角形的对应角相等
探究三角形全等的条件
能够完全重合的两个三角形
1.一个元素(边或角)
两个三角形不一定全等
2.两个元素(边或角)
两个三角形不一定全等
3.三个元素(边或角)
两个三角形可能全等
谢谢观看!
12.2.1全等三角形的判定条件
第12章 全等三角形
【2025新教材】华东师大版数学 八年级上册
授课教师:********
班 级:********
时 间:********
全等三角形的判定条件教案
一、教学目标
知识与技能目标:学生能够准确阐述全等三角形的判定条件,包括 “边边边”(SSS)、“边角边”(SAS)、“角边角”(ASA)、“角角边”(AAS)和 “斜边、直角边”(HL,适用于直角三角形);熟练运用这些判定条件判断两个三角形是否全等,能够在具体图形中准确找出对应边和对应角,并依据判定条件进行推理证明;学会利用全等三角形的判定条件解决实际问题,如测量不可直接到达的距离等。
过程与方法目标:通过动手操作、观察、猜想、验证等活动,引导学生经历全等三角形判定条件的探究过程,培养学生的自主探究能力和逻辑推理能力;在运用判定条件解决问题的过程中,提高学生的分析问题、解决问题的能力,让学生体会分类讨论、转化等数学思想方法。
情感态度与价值观目标:激发学生对几何知识的学习兴趣,感受数学与生活的紧密联系;在探究活动中,培养学生勇于探索、敢于质疑的精神,增强学生学习数学的自信心;通过小组合作学习,培养学生的团队协作意识和交流表达能力。
二、教学重难点
教学重点:深入理解并熟练掌握全等三角形的判定条件,能够准确运用这些条件判定两个三角形是否全等;掌握判定条件在不同几何图形和实际问题中的应用方法,这是全等三角形知识的核心,也是后续学习相似三角形、四边形等几何知识的重要基础。
教学难点:在复杂的图形中准确识别对应边和对应角,避免因对应关系错误导致判定失误;理解判定条件的适用范围和限制条件,如 “边边角”(SSA)和 “角角角”(AAA)不能判定两个三角形全等的原因;在实际问题中,能够将问题转化为全等三角形的判定问题,并选择合适的判定条件进行求解,这对学生的空间想象能力和综合运用能力要求较高。
三、教学方法
讲授法:系统讲解全等三角形判定条件的概念、内容和应用要点,确保学生理解核心知识和关键内容。
实验探究法:组织学生进行动手操作实验,如用小棒拼三角形、用纸张裁剪三角形等,通过实验探究全等三角形的判定条件,培养学生的自主探究能力和实践操作能力。
范例教学法:通过典型的例题和练习题,展示全等三角形判定条件的应用技巧和解题思路,让学生掌握正确的解题步骤和书写规范。
小组合作学习法:组织学生开展小组合作学习活动,共同探讨全等三角形判定中的疑难问题,交流学习经验和方法,培养学生的团队协作能力和交流表达能力。
多媒体辅助教学法:利用多媒体课件展示几何图形的动态变化,帮助学生更直观地理解全等三角形的判定条件,增强教学的直观性和趣味性。
四、教学过程
(一)复习导入(5 分钟)
回顾全等三角形概念:提问学生全等三角形的定义,即能够完全重合的两个三角形叫做全等三角形,引导学生回顾全等三角形的对应边相等、对应角相等的性质。
引发思考:教师提出问题:“在实际问题中,我们很难通过将两个三角形重合来判断它们是否全等,那么是否有更简便的方法呢?今天我们就来探究全等三角形的判定条件。” 由此导入本节课的课题。
(二)新课讲授
“边边边”(SSS)判定条件的探究(15 分钟)
实验操作:给每个小组发放三根长度固定的小棒(如 3cm、4cm、5cm),让学生用小棒拼出三角形。引导学生观察发现,无论怎样拼接,得到的三角形形状和大小都相同。
猜想归纳:组织学生进行小组讨论,根据实验现象猜想:三边对应相等的两个三角形全等。
验证证明:教师通过多媒体课件展示两个三边对应相等的三角形,利用平移、旋转、翻折等操作,证明这两个三角形能够完全重合,从而得出 “边边边” 判定条件:三边对应相等的两个三角形全等,可以简写成 “边边边” 或 “SSS”。
应用讲解:以一个简单的几何图形为例,如已知在△ABC 和△DEF 中,AB = DE = 3cm,BC = EF = 4cm,AC = DF = 5cm,讲解如何运用 “SSS” 判定条件证明△ABC≌△DEF,强调书写证明过程的规范格式。
“边角边”(SAS)判定条件的探究(15 分钟)
实验操作:让学生在纸上画出一个三角形,使其中两条边的长度分别为 3cm 和 4cm,这两条边的夹角为 60°。然后小组内成员互相比较所画的三角形,观察发现这些三角形形状和大小相同。
猜想归纳:引导学生猜想:两边和它们的夹角对应相等的两个三角形全等。
验证证明:教师利用几何画板软件,动态展示两个满足 “两边和它们的夹角对应相等” 条件的三角形,通过图形变换证明这两个三角形全等,得出 “边角边” 判定条件:两边和它们的夹角对应相等的两个三角形全等,可以简写成 “边角边” 或 “SAS”。同时强调 “夹角” 的重要性,通过反例说明 “边边角”(SSA)不能判定两个三角形全等。
应用讲解:给出例题,如在△ABC 和△DEF 中,AB = DE = 3cm,∠B = ∠E = 60°,BC = EF = 4cm,讲解如何运用 “SAS” 判定条件证明△ABC≌△DEF,规范证明过程的书写。
“角边角”(ASA)和 “角角边”(AAS)判定条件的探究(20 分钟)
“角边角”(ASA)探究:先让学生思考:如果已知两个三角形的两个角及其夹边对应相等,这两个三角形是否全等?然后通过画三角形的方式进行验证,例如画一个三角形,使两个角分别为 30° 和 60°,它们的夹边为 5cm,小组内比较所画三角形,得出猜想。教师通过几何证明,得出 “角边角” 判定条件:两角和它们的夹边对应相等的两个三角形全等,可以简写成 “角边角” 或 “ASA”。
“角角边”(AAS)探究:引导学生思考:如果两个角和其中一个角的对边对应相等,能否判定两个三角形全等?利用三角形内角和定理,将 “角角边” 的情况转化为 “角边角” 的情况进行证明,从而得出 “角角边” 判定条件:两角和其中一个角的对边对应相等的两个三角形全等,可以简写成 “角角边” 或 “AAS”。
应用讲解:通过多个例题,如在△ABC 和△DEF 中,∠A = ∠D = 30°,∠B = ∠E = 60°,AB = DE = 5cm(ASA 判定);在△ABC 和△DEF 中,∠A = ∠D = 30°,∠C = ∠F = 90°,BC = EF = 4cm(AAS 判定),讲解如何运用这两个判定条件进行证明,强化学生对判定条件的理解和应用能力。
“斜边、直角边”(HL)判定条件的探究(10 分钟)
情境引入:教师提出问题:对于两个直角三角形,除了前面的判定条件,是否有特殊的判定方法呢?引导学生思考。
探究证明:让学生画出两个直角三角形,使它们的斜边和一条直角边分别相等,然后通过测量、叠合等方式进行验证。教师再通过几何推理证明,得出 “斜边、直角边” 判定条件:斜边和一条直角边对应相等的两个直角三角形全等,可以简写成 “斜边、直角边” 或 “HL”。强调该判定条件只适用于直角三角形。
应用讲解:给出直角三角形全等判定的例题,如在 Rt△ABC 和 Rt△DEF 中,∠C = ∠F = 90°,AB = DE = 5cm,AC = DF = 3cm,讲解如何运用 “HL” 判定条件证明 Rt△ABC≌Rt△DEF。
(三)课堂练习(15 分钟)
如图,已知 AB = AD,CB = CD,求证:△ABC≌△ADC。
如图,AB = AC,AD = AE,∠BAC = ∠DAE,求证:△ABD≌△ACE。
如图,已知∠A = ∠D,∠B = ∠E,BC = EF,求证:△ABC≌△DEF。
如图,在 Rt△ABC 和 Rt△DEF 中,∠C = ∠F = 90°,AC = DF,AB = DE,求证:Rt△ABC≌Rt△DEF。
让学生独立完成练习,教师巡视课堂,及时发现学生存在的问题,进行个别辅导和集中讲解。针对学生在判定条件应用、对应关系确定、证明过程书写等方面出现的错误进行重点分析,帮助学生掌握正确的解题思路和方法。
(四)课堂小结(5 分钟)
请学生回顾本节课所学内容,分享自己对全等三角形判定条件的理解和收获,以及在学习过程中遇到的困难和解决方法。
教师进行系统总结:强调整体回顾全等三角形的判定条件,包括 “SSS”“SAS”“ASA”“AAS” 和 “HL”,明确每个判定条件的内容、适用范围和注意事项;总结在运用判定条件进行证明时的要点,如准确找出对应边和对应角、规范书写证明过程等;鼓励学生在课后继续加强练习,熟练掌握全等三角形的判定条件,提高几何推理能力。
(五)作业布置(1 分钟)
必做题:课本习题 [对应章节] 第 1 - 5 题,帮助学生巩固全等三角形判定条件的基础知识和基本技能。
选做题:在实际生活中寻找一个可以用全等三角形判定条件解决的问题,并尝试进行解答,如测量池塘两端的距离等,让学生将所学知识应用到实际生活中,提高知识应用能力。
这份教案围绕全等三角形判定条件设计教学环节。你若对教学情境、探究活动、练习难度等方面有新想法,欢迎提出,我们可进一步优化完善。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1、理解并掌握全等三角形的概念,及全等三角形经过一系列变换后,能够完全重合的性质;
2、掌握全等三角形的性质(对应边相等,对应角相等)和全等的判定条件;
下图中的几组图形有怎样的关系?
(1)
(2)
(3)
思考:你能想到现实生活中有这样的图形吗?
能够完全重合的两个图形叫做全等图形.
全等形包括规则图形和不规则图形全等.
全等图形:
知识点一 全等三角形的概念
全等三角形
能够完全重合的两个三角形是全等三角形.
A
B
C
A′
B′
C′
能相互重合的顶点是对应顶点.
能相互重合的边是对应边.
能相互重合的角是对应角.
A与A′、B与B′、C与C′
AB与A′B′、BC与B′C′ 、CA与C′A′
∠A与∠A′、∠B与∠B′、∠C与∠C′
A
B
C
A′
B′
C′
全等三角形的性质:
全等三角形的对应边相等,对应角相等.
全等三角形的表示:
“全等”用符号“≌”来表示,读作“全等于”.
记两个三角形全等时,要把表示对应顶点的字母写在对应的位置上.
记作△ABC≌△A′B′C′
1.怎样改变其中一个图形的位置可以得到另一个图形?
观察与思考
2.你能在以下图案中能找出全等图形吗?
做
一
做
如图,以直线 l 为对称轴,画出△ABC 的对称图形,并指出它们的对应顶点﹑对应边和对应角.
若已知∠A=60°,∠B=80°,则
∠D=_____,∠E=_____,∠F=_____.
60°
80°
40°
典例精析
【例1】 如图,将△ABC 绕点 B 按顺时针方向旋转 60°后得△A′BC′.指出对应顶点、对应边和对应角.
解: 对应顶点: A 与A′,B 与B,C 与 C′;
对应边: AB 与 A′B,AC 与 A′C′,BC 与 BC′.
对应角:∠CBA 与∠C′BA′,∠A 与∠A′,
∠C 与∠C′.
练一练
【解析】∵ △ABC ≌ △DEF,
∴ ∠ACB = ∠DFE.
∴∠DFE = 180°-(∠A +∠B)=85°.
1. 如图,已知△ABC ≌△DEF,∠A =40°, ∠B =55°,则∠DFE 的度数是________.
85°
知识点二 全等三角形的判定条件
怎么判断两个三角形全等呢?
根据全等三角形的定义可知:能够完全重合两个三角形全等,即两个三角形的三对边、三对角分别对应相等,则两个三角形全等.
能否减少一些条件,找到更简便的判定两个三角形全等的方法呢?
对两个三角形来说,六个元素(三条边、三对角)中至少要有几个元素对应相等,这两个三角形才会全等呢?
1.画几个有一边长为8cm的三角形,这样得到的三角形是否全等?
如果两个三角形只有一组对应相等的元素,那么会出现几种情况?这两个三角形会全等吗?
探究活动1
两种,一条边或一个角相等.
试一试
有一条边对应相等的三角形不一定全等.
有一个角对应相等的三角形不一定全等.
2.画几个有一个角为60°的三角形,这样得到的三角形是否全等?
(
60°
归纳:如果两个三角形只有一组对应相等的元素,那么这两个三角形不一定全等.
30°
(1)三角形的一条边为3cm,一个内角为30°
3cm
3cm
3cm
30°
30°
探究活动2
如果两个三角形有两组对应相等的元素,那么会出现几种可能的情况?这两个三角形会全等吗?
三种,一条边和一个角相等;两个角相等;两条边相等.
试一试
按照下面的条件,用刻度尺和量角器画三角形,并和周围的同学比较,所画的图形是否全等.
一条边和一个内角相等不能判定两个三角形全等.
(
(
(
30°
70°
30°
70°
30°
70°
(2)三角形的两个内角分别为30°和70°.
两个内角对应相等不能判定两个三角形全等.
5cm
3cm
3cm
(3)三角形的两条边分别为3cm和5cm.
两条边对应相等不能判定两个三角形全等.
两个三角形只有一组或两组对应相等的元素(边或角),那么这两个三角形不一定全等.
探索发现
思 考
如果两个三角形有三组对应相等的元素(边或角),又会如何呢?
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,最小的边是对应边
(长对长,短对短,中对中);
(5)两个全等三角形最大的角是对应角,最小的角是对应角
(大角对大角,小角对小角);
找对应边、对应角的方法总结:
典例精析
例2 如图,△ABC≌△DEF,∠A=60°,∠E=40°,BF=3,EF=6,求∠DFE的度数和CF的长.
E
D
B
F
A
C
3
60°
40°
6
解:∵△ABC≌△DEF,∠A=60°,
∠E=40°,BF=3,EF=6,
∴∠D=∠A=60°,BC=EF=6,
∴∠DFE=180°-∠E-∠D
=180°-40°-60°
=80°
CF=BC-BF=6-3=3.
练一练
如图,将△AOB 绕点 O 旋转180°,得到△COD,这时△AOB≌△_____. 这两个三角形的对应边是:AO与______,OB与_______,BA与_______;
对应角是:∠AOB与_______,∠OBA与______,
∠BAO与________.
COD
CO
OD
DC
∠COD
∠ODC
∠DCO
2. 如图,AD // BC,AD = BC,AE⊥BC,将△ABE 沿 AD 方向平移,使点 A 与点 D 重合,点 E 平移至点 F, 则△ABE≌______,∠F =_____°.
△DCF
90
1.如图,△ABC ≌△ CED, ∠ B和∠ DEC是对应角,BC与ED是对应边,说出另两组对应角和对应边.
A
B
C
E
D
解: 对应角: ∠ A= ∠ DCE, ∠ D= ∠ ACB;
对应边: AC=CD,AB=CE.
2.下列各组中是全等图形的是( )
A. 两个周长相等的等腰三角形
B. 两个面积相等的长方形
C.两条长度的圆弧
D. 两个周长相等的圆
D
解:周长相等,圆的半径也相等,故两个周长相等的圆全等;
1. 下列说法正确的是( )
B
A. 三个角对应相等的两个三角形全等
B. 判定两个三角形全等的条件中至少有一个条件是边相等
C. 面积相等的两个三角形全等
D. 周长相等的两个三角形全等
返回
2. [2025泰安期末]根据下列已知条件,能画出唯一的
的是( )
C
A. ,
B. ,,
C. , ,
D. ,,
返回
3. 如图,把以点 为旋转中心逆时
针旋转得到,点, 的对应点分
别是点,,且点在 的延长线上,
连结 ,则下列结论一定正确的是( )
A
A. B.
C. D.
返回
(第4题)
4. 如图,将折叠,使点与 边的
中点重合,折痕为.若 ,
,则 的周长为( )
A
A. 12 B. 13 C. 14 D. 15
返回
(第5题)
5.[2025重庆校级期末]两个全等
的直角三角形重叠在一起,将其中
的一个三角形沿着 方向平移到
的位置,, ,
平移距离为2,则阴影部分面积为
___.
7
(第5题)
【点拨】由平移的性质知
, ,
,
,
.
返回
6.如图,将绕点顺时针旋转 得
到, .
(1)和 是否全等?如果全等,
请写出对应边和对应角.
【解】 .
对应边:和,和,和 ;
对应角:和,和, 和
.
(2)直线与直线 有怎样的位置关系?请说明理由.
.
理由:延长交 于点
,
, ,
,
即点,, 在同一直线上.
, ,
, ,
.
返回
7. 图中的小正方形边长都相等,若
,则点 可能是图中的
( )
D
A. 点 B. 点 C. 点 D. 点
返回
8. 一个三角形三条边的长分别是5,7,10,
另一个三角形三条边的长分别是, ,5.若这两个
三角形全等,则 的值为( )
D
A. 7 B. C. 8 D. 或7
【点拨】分两种情况讨论: 解得
;解得
.综上所述,的值是 或7.
返回
9.[2025武汉月考]如图①,数轴上从左至右依次有, ,
,,五个点,其中点,,表示的数分别为 ,0,
4.如图②,将数轴在点的左侧部分绕点 顺时针方向旋转
,将数轴在点的右侧部分绕点逆时针方向旋转 ,
连结,.若和全等,则点 表示的数为
_______________.
或
全等三角形
定义
性质
1.全等三角形的对应边相等
2.全等三角形的对应角相等
探究三角形全等的条件
能够完全重合的两个三角形
1.一个元素(边或角)
两个三角形不一定全等
2.两个元素(边或角)
两个三角形不一定全等
3.三个元素(边或角)
两个三角形可能全等
谢谢观看!
