12.2.3三角形全等的判定-角边角 课件(共37张PPT)
文档属性
| 名称 | 12.2.3三角形全等的判定-角边角 课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 15:43:35 | ||
图片预览




文档简介
(共37张PPT)
12.2.3三角形全等的判定-角边角
第12章 全等三角形
【2025新教材】华东师大版数学 八年级上册
授课教师:********
班 级:********
时 间:********
《三角形全等的判定 - 角边角》教案
一、教学目标
(一)知识与技能目标
学生能够深刻理解并熟练掌握三角形全等的 “角边角”(ASA)判定定理,准确运用几何语言对其进行表述。
学会灵活运用 “角边角” 判定定理证明两个三角形全等,规范证明过程的书写格式,提升逻辑推理能力。
(二)过程与方法目标
引导学生经历探索三角形全等条件的全过程,体会从特殊到一般、分类讨论的数学思想,通过画图、裁剪、对比、归纳等活动,培养自主探究能力和创新思维。
增强学生在实际问题中抽象出数学模型,并运用 “角边角” 判定定理解决问题的能力,感受数学与生活的紧密联系。
(三)情感态度与价值观目标
通过小组合作交流,培养学生的团队协作精神和勇于探索、积极思考的科学态度。
让学生在成功解决问题的过程中,体验数学学习的乐趣,增强学习数学的自信心和成就感,激发学习数学的浓厚兴趣。
二、教学重难点
(一)教学重点
透彻理解并牢固掌握 “角边角” 判定两个三角形全等的方法及其应用。
熟练掌握分析证明思路的方法,规范书写三角形全等的证明过程。
(二)教学难点
深入探索 “角边角” 判定定理的推导过程,理解其内在逻辑。
能在复杂图形中准确识别全等三角形以及所需的对应角、对应边条件。
三、教学方法
讲授法:系统讲解 “角边角” 判定定理的内容、几何语言表达及应用要点,确保学生清晰理解基础知识。
探究法:组织学生开展画图、动手操作等探究活动,自主发现 “角边角” 判定三角形全等的规律,培养自主学习能力。
讨论法:引导学生在小组内或班级中围绕探究发现、证明思路等问题展开讨论,促进思想交流,培养合作与表达能力。
练习法:通过有针对性的练习题,让学生在实践中巩固 “角边角” 判定定理,提高运用知识解决问题的能力。
四、教学过程
(一)复习导入(5 分钟)
回顾全等三角形的定义及性质,提问学生进行回答,强化记忆:
定义:能够完全重合的两个三角形叫做全等三角形。
性质:全等三角形的对应边相等,对应角相等。
复习已学的三角形全等判定方法 “边边边”(SSS)和 “边角边”(SAS),提问学生判定定理的内容,引导学生思考是否还有其他判定三角形全等的方法,从而引出本节课主题 —— 探索三角形全等的 “角边角” 判定方法。
(二)探究新知(20 分钟)
提出问题
展示问题:如果已知两个三角形的两个角和一条边对应相等,那么这两个三角形一定全等吗?
引导学生对 “两角一边” 的位置关系进行分类讨论,得出两种情况:两角及其夹边对应相等;两角及其中一角的对边对应相等(为后续学习 “AAS” 埋下伏笔)。
探究两角及其夹边对应相等的情况
操作实验:
让学生在练习本上画一个△ABC,使∠A = 60°,AB = 4cm,∠B = 45°。具体画图步骤如下:
画线段 AB = 4cm;
以点 A 为顶点,AB 为一边,画∠MAB = 60°;
以点 B 为顶点,BA 为一边,画∠NBA = 45°,射线 AM 与射线 BN 相交于点 C。
学生完成画图后,用剪刀剪下自己画的三角形,与同桌的三角形进行叠合比较,观察能否完全重合。
小组讨论:组织学生在小组内交流自己的发现,讨论通过这种方式画出的三角形是否全等。
归纳总结:
邀请几个小组代表发言,分享小组讨论结果。
教师根据学生的回答进行总结:经过大量的实验和验证可知,两角及其夹边对应相等的两个三角形全等。这就是三角形全等的 “角边角” 判定定理,简写成 “ASA”。
用几何语言表示为:在△ABC 和△DEF 中,
\(\begin{cases}∠A = ∠D\\AB = DE\\∠B = ∠E\end{cases}\),
所以△ABC ≌△DEF(ASA)。
(三)例题讲解(15 分钟)
例 1:已知:如图,在△ABC 和△DEF 中,∠A = ∠D,AB = DE,∠B = ∠E,求证:△ABC ≌△DEF。
分析:
明确题目中直接给出了满足 “角边角” 判定定理的三个条件。
按照 “角边角” 的顺序,将对应条件清晰罗列。
证明:在△ABC 和△DEF 中,
\(\begin{cases}∠A = ∠D\\AB = DE\\∠B = ∠E\end{cases}\)
所以△ABC ≌△DEF(ASA)。
例 2:已知:如图,点 B、F、C、E 在同一条直线上,FB = CE,∠B = ∠E,∠ACB = ∠DFE,求证:△ABC ≌△DEF。
分析:
由已知 FB = CE,根据等式性质,可得 FB + FC = CE + FC,即 BC = EF。
此时,在△ABC 和△DEF 中,有∠B = ∠E,BC = EF,∠ACB = ∠DFE,满足 “角边角” 判定定理的条件。
证明:
因为 FB = CE,
所以 FB + FC = CE + FC,即 BC = EF。
在△ABC 和△DEF 中,
\(\begin{cases}∠B = ∠E\\BC = EF\\∠ACB = ∠DFE\end{cases}\)
所以△ABC ≌△DEF(ASA)。
强调:
运用 “角边角” 判定定理证明三角形全等时,要严格按照两角及其夹边的顺序准确列出三个条件,并且对应顶点的字母必须写在对应的位置上。
注意观察图形,挖掘题目中隐含的条件,如通过线段的和差关系得到对应边相等,利用对顶角相等、公共角等得到对应角相等。
(四)课堂练习(10 分钟)
已知:如图,∠1 = ∠2,∠3 = ∠4,求证:△ABC ≌△ABD。
如图,在△ABC 中,AD⊥BC 于点 D,BE⊥AC 于点 E,AD 与 BE 相交于点 F,且∠CAD = ∠CBE,AC = BC,求证:△ADC ≌△BEC。
已知:如图,AB∥CD,AF = CE,∠B = ∠D,求证:△ABF ≌△CDE。
学生独立完成练习,教师巡视指导,及时发现并纠正学生在证明过程中出现的问题,如条件罗列顺序错误、对应顶点字母书写不规范等。选取部分学生的答案进行展示和点评,针对共性问题进行集中讲解。
(五)课堂小结(5 分钟)
与学生一起回顾本节课所学内容:
“角边角”(ASA)判定定理:两角及其夹边对应相等的两个三角形全等,明确其几何语言表述。
证明三角形全等的思路和步骤:先分析已知条件,找出满足 “角边角” 判定定理的对应角和对应边;再指明在哪两个三角形中进行全等证明;最后按照定理要求列出条件,得出结论。
强调运用 “角边角” 判定定理时的注意事项,如条件的顺序、对应顶点的书写以及挖掘隐含条件的重要性。
鼓励学生分享本节课的学习收获和体会,包括对知识的理解、学习方法的掌握以及在小组合作中的感受等。教师进行补充和总结,进一步强化重点内容,解答学生的疑问。
(六)布置作业(5 分钟)
必做题:教材课后练习题第 X 题、第 X 题,帮助学生巩固本节课所学的基础知识和基本技能。
选做题:已知:如图,在四边形 ABCD 中,AB∥CD,∠B = ∠D,求证:△ABC ≌△CDA,提高学生运用知识解决综合性问题的能力。
拓展题:如图,在△ABC 和△A'B'C' 中,∠A = ∠A',∠B = ∠B',BC = B'C',试探究△ABC 与△A'B'C' 是否全等,并说明理由,引导学生思考 “角角边” 与 “角边角” 的联系,为后续学习做铺垫 。
五、教学反思
在本节课教学中,通过多种教学方法引导学生探究 “角边角” 判定定理,注重学生的动手操作和思维训练。但在教学过程中,可能存在部分学生对定理的应用不够灵活,在复杂图形中难以快速准确找到对应条件的情况。在今后的教学中,应增加更多不同类型、不同难度层次的练习题,加强对学生分析问题和解决问题能力的培养。同时,进一步关注学生在小组合作中的参与度和表现,确保每个学生都能在合作学习中有所收获和提高。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1、通过画图、操作、实验等教学活动,探索三角形全等的判定方法(A.S.A.,A.A.S.);
2、会用A.S.A.,A.A.S.判定两个三角形全等;
3、灵活地运用所学的判定方法判定两个三角形全等,从而解决线段或角相等的问题;
温故知新
上节课,我们得到了全等三角形的一种判定方法,还记得吗?
S.A.S.
现在我们讨论两角一边的情况:如果两个三角形有两个角、一条边分别对应相等,那么这两个三角形全等吗?
(角边角)
(角角边)
可以分成两种情况:(1)两个角及这两角的夹边;
(2)两个角及其中一角的对边.
问题:如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带哪一块去呢?你能帮这位同学出主意吗?
知识点一 角边角判定三角形全等
操作1:如图,用纸板挡住了两个三角形的一部分,你能画出这两个三角形吗?如果能,你画的三角形与其他同学画的三角形能完全重合吗?
相当于已知一角画三角形,我们可以画出无数个不同形状、大小的三角形.
三角形能唯一确定.
4
60°
45°
F
E
D
4
45°
60°
A
B
C
4
60°
R
Q
P
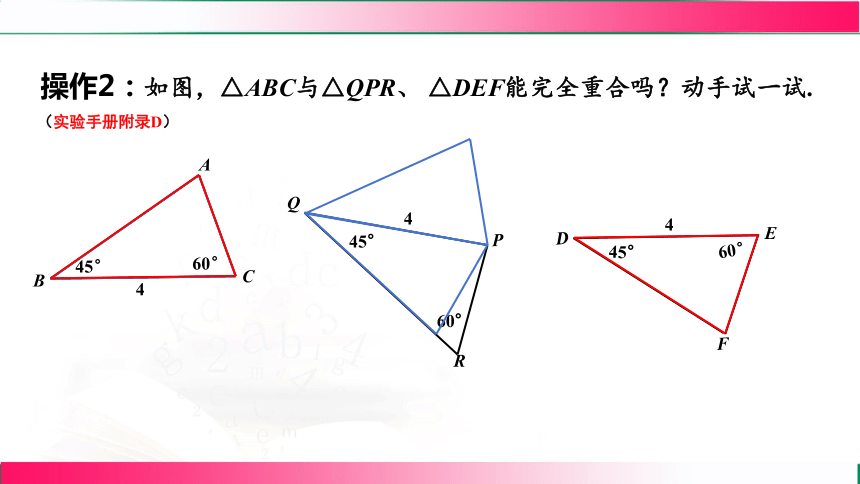
操作2:如图,△ABC与△QPR、 △DEF能完全重合吗?动手试一试.
(实验手册附录D)
45°
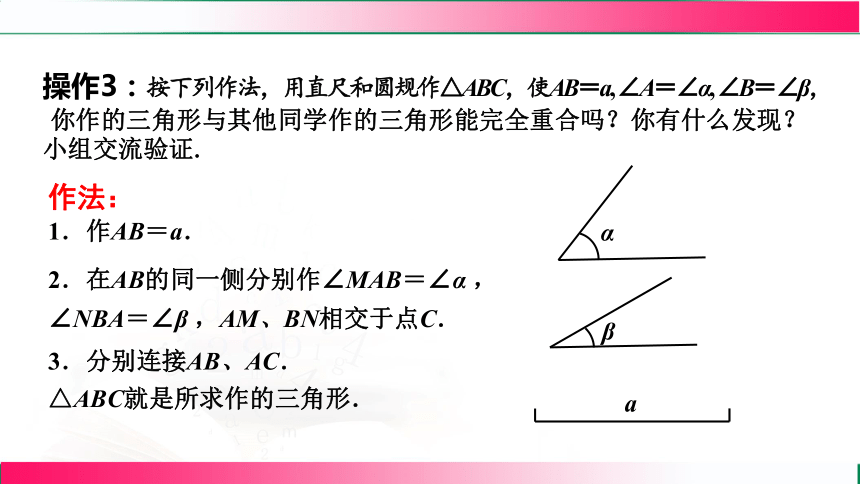
操作3:按下列作法,用直尺和圆规作△ABC,使AB=a, ∠A=∠α, ∠B=∠β,
1你作的三角形与其他同学作的三角形能完全重合吗?你有什么发现?
作法:
1.作AB=a.
2.在AB的同一侧分别作∠MAB=∠α ,∠NBA=∠β ,AM、BN相交于点C.
3.分别连接AB、AC.
△ABC就是所求作的三角形.
α
a
小组交流验证.
β
知识要点
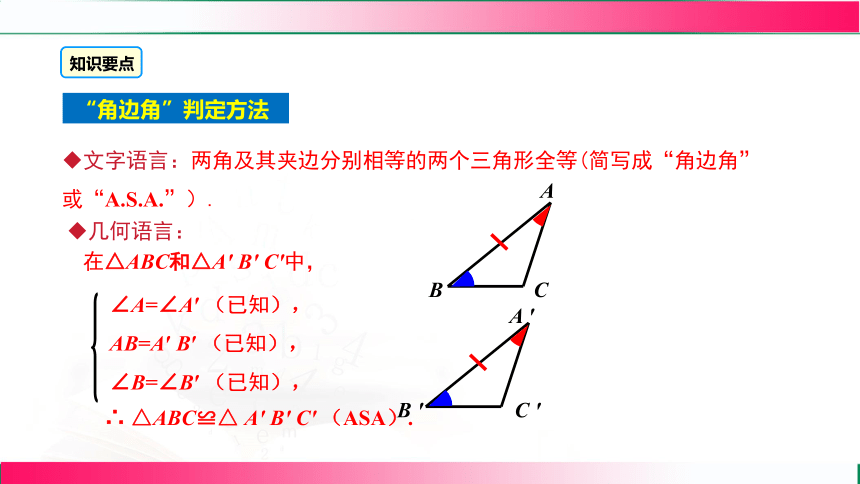
“角边角”判定方法
文字语言:两角及其夹边分别相等的两个三角形全等(简写成“角边角”或“A.S.A.”).
几何语言:
∠A=∠A′ (已知),
AB=A′ B′ (已知),
∠B=∠B′ (已知),
在△ABC和△A′ B′ C′中,
∴ △ABC≌△ A′ B′ C′ (ASA).
A
B
C
A ′
B ′
C ′
典例精析
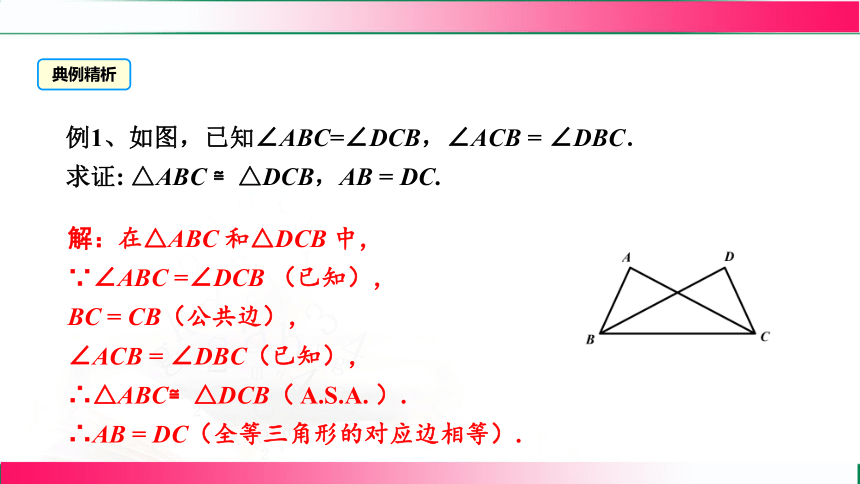
例1、如图,已知∠ABC=∠DCB,∠ACB = ∠DBC.
求证: △ABC ≌△DCB,AB = DC.
解:在△ABC 和△DCB 中,
∵∠ABC =∠DCB (已知),
BC = CB(公共边),
∠ACB = ∠DBC(已知),
∴△ABC≌△DCB( A.S.A. ).
∴AB = DC(全等三角形的对应边相等).
例2 已知:如图,在△ABC中,D是BC的中点,点E、F分别在AB、AC上,且DE//AC,DF//AB.
求证:BE=DF,DE=CF.
E
A
B
C
D
F
证明:∵DE∥AC,DF∥AB(已知),
∴∠EDC=∠C,∠B=∠FDC (两直线平行,同位角相等).
∵D是线段BC的中点(已知),
∴BD=DC(线段中点定义).
在△EBD和△FDC中,
∴△EBD≌△FDC(ASA),
∴BE=DF,DE=CF(全等三角形对应边相等).
练一练
1.如图,∠C=∠E,∠1=∠2,BA=DA,你能证明BC=DE吗
A
E
D
C
B
1
2
证明:∵ ∠1=∠2 (已知),
∴ ∠1+∠DAC=∠2+∠DAC (等式性质),
∴ ∠BAC=∠DAE.
在△BAC和△DAE中,
∴△BAC≌△DAE(ASA),
∴AC=DE(全等三角形的对应边相等).
2.已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C
(1)求证:△ABE≌△ACD
A
B
C
D
E
O
解:(1)证明 :在△ADC和△AEB中
∴△ACD≌△ABE(ASA)
(2) ∵△ACD≌△ABE(已证)
∴AD=AE(全等三角形的对应边相等)
又∵AB=AC(已知)
∴AB-AD=AC-AE(等式性质)
∴BD=CE
(2) BD和CE相等吗
知识点二 角角边判定三角形全等
(角角边)
如图,如果两个三角形有两个角分别对应相等,且其中一组相等的角的对边相等,那么这两个三角形是否一定全等?
思 考
分析:因为三角形的内角和等于180°,因此有两个角对应相等,那么第三个角必定对应相等,于是有“角边角”,可证得这两个三角形全等.
已知:如图,∠A=∠A′,∠B=∠B′,AC=A′C′.
求证: △ABC≌△A′B′C′.
证明:∵∠A=∠A′,∠B=∠B′,
∠A+∠B+∠C=180°,
∠A′+∠B′+∠C′=180°(三角形内角和等于180°),
∴∠C=∠C′(等量代换).
在△ABC和△A′B′C′中,
∵∠A=∠A′,
AC=A′C′,
∠C=∠C′,
∴△ABC≌△A′B′C′(A.S.A.)
知识要点
“角角边”判定方法
文字语言:有两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“A.A.S.”).
几何语言:
∠A=∠A′ (已知),
∠B=∠B′ (已知),
AC=A′ C′ (已知),
在△ABC和△A′ B′ C′中,
∴ △ABC≌△ A′ B′ C′ (A.A.S.).
A
B
C
A ′
B ′
C ′
典例精析
例3 如图,点D在AB上,点E在AC上,AD=AE, ∠B=∠C,
求证:AB=AC.
A
B
C
D
E
分析:证明△ACD≌△ABE,就可以得出AB=AC.
证明:在△ACD和△ABE中,
∠A=∠A(公共角 ),
∠C=∠B (已知 ),
AD=AE(已知),
∴ △ACD≌△ABE(A.A.S.),
∴AB=AC.
方法归纳:通常利用全等三角形的对应边相等来证明两条线段相等,这是一个重要的方法.类似的方法可以证明两个角相等.
例4.已知:如图, AB⊥BC,AD⊥DC,∠1=∠2, 求证:AB=AD.
A
C
D
B
1
2
证明: ∵ AB⊥BC,AD⊥DC,
∴ ∠ B=∠D=90 °.
在△ABC和△ADC中,
∠1=∠2 (已知),
∠ B=∠D(已证),
AC=AC (公共边),
∴ △ABC≌△ADC(A.A.S.).
∴AB=AD.
练一练
1、如图,在△ABC中,D 是边 BC 的中点,过点C 画直线 CE,使 CE// AB,交 AD 的延长线于点 E.求证: AD = ED.
证明: CE // AB (已知),
∵∠ABD = ∠ECD,∠BAD = ∠CED (两直线平行,内错角相等).
在△ABD 与 △ECD 中,
∵∠ABD = ∠ECD,∠BAD = ∠CED (已证),
BD = CD (已知),
∴△ABD≌△ECD ( A.A.S. ) ,
∴AD = ED (全等三角形的对应边相等).
D
A
C
B
证明:(已知)
∴________________(两直线平行,内错角相等)
又(已知)
∴_________________(等式的性质)
在和中
(________)
(全等三角形的对应边相等).
∠ADB=∠CBD
∠ABD=∠CDB
∠ADB=∠CBD
BD=DB
∠ABD=∠CDB
ASA
1.如图,已知.请将下列说明的理由补充完整.
1. 打碎的一块三角形玻璃如图所示,现在
要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
A. 带①④去 B. 带②③去 C. 带③④去 D. 带②④去
√
返回
(第2题)
2. [2025武汉江夏区期中]如图,在
和中,点,, 在同
一直线上,已知 ,
,添加以下条件后,仍不能
判定 的是( )
A. B.
C. D.
√
返回
(第3题)
3. 如图,在中, ,
,于点,于点 ,
,,则 的长是( )
A. B.
C. D.
√
(第3题)
【点拨】 , ,
,
,
, ,
.
在和 中,
,
, ,
.
(第3题)
返回
4.如图,已知,由尺规作图痕迹可知 ,
全等的理由为_____.
(第4题)
返回
5.如图,点,,,在同一条直线上, ,
,.若 , ,则
的度数为_____ .
110
(第5题)
(第5题)
【点拨】, .在
和 中,
,
,
.
返回
6. 如图,,,,
四点在一条直线上, ,
,老师说:再添加一个条件就
可以使 .下面是课堂上
(1)甲、乙、丙三个同学说法正确的是________;
甲、丙
三个同学的发言,甲说:添加 ,乙说:添加
;丙说:添加 .
(2)请你从正确的说法中选择一种,给出你的证明.
【解】(二选一即可)选择甲.证明如
下:
, .
在和中,
.
或选择丙.证明如下:
, .
,.在和 中,
.
返回
7. 在中, ,将
沿图中虚线剪开,剪下的两个三角形不一定全等的是
( )
A. B. C. D.
√
角边角
判定定理
角边角
应用角边角、角角边判定三角形全等
应用
角角边
应用角边角、角角边解决问题
谢谢观看!
12.2.3三角形全等的判定-角边角
第12章 全等三角形
【2025新教材】华东师大版数学 八年级上册
授课教师:********
班 级:********
时 间:********
《三角形全等的判定 - 角边角》教案
一、教学目标
(一)知识与技能目标
学生能够深刻理解并熟练掌握三角形全等的 “角边角”(ASA)判定定理,准确运用几何语言对其进行表述。
学会灵活运用 “角边角” 判定定理证明两个三角形全等,规范证明过程的书写格式,提升逻辑推理能力。
(二)过程与方法目标
引导学生经历探索三角形全等条件的全过程,体会从特殊到一般、分类讨论的数学思想,通过画图、裁剪、对比、归纳等活动,培养自主探究能力和创新思维。
增强学生在实际问题中抽象出数学模型,并运用 “角边角” 判定定理解决问题的能力,感受数学与生活的紧密联系。
(三)情感态度与价值观目标
通过小组合作交流,培养学生的团队协作精神和勇于探索、积极思考的科学态度。
让学生在成功解决问题的过程中,体验数学学习的乐趣,增强学习数学的自信心和成就感,激发学习数学的浓厚兴趣。
二、教学重难点
(一)教学重点
透彻理解并牢固掌握 “角边角” 判定两个三角形全等的方法及其应用。
熟练掌握分析证明思路的方法,规范书写三角形全等的证明过程。
(二)教学难点
深入探索 “角边角” 判定定理的推导过程,理解其内在逻辑。
能在复杂图形中准确识别全等三角形以及所需的对应角、对应边条件。
三、教学方法
讲授法:系统讲解 “角边角” 判定定理的内容、几何语言表达及应用要点,确保学生清晰理解基础知识。
探究法:组织学生开展画图、动手操作等探究活动,自主发现 “角边角” 判定三角形全等的规律,培养自主学习能力。
讨论法:引导学生在小组内或班级中围绕探究发现、证明思路等问题展开讨论,促进思想交流,培养合作与表达能力。
练习法:通过有针对性的练习题,让学生在实践中巩固 “角边角” 判定定理,提高运用知识解决问题的能力。
四、教学过程
(一)复习导入(5 分钟)
回顾全等三角形的定义及性质,提问学生进行回答,强化记忆:
定义:能够完全重合的两个三角形叫做全等三角形。
性质:全等三角形的对应边相等,对应角相等。
复习已学的三角形全等判定方法 “边边边”(SSS)和 “边角边”(SAS),提问学生判定定理的内容,引导学生思考是否还有其他判定三角形全等的方法,从而引出本节课主题 —— 探索三角形全等的 “角边角” 判定方法。
(二)探究新知(20 分钟)
提出问题
展示问题:如果已知两个三角形的两个角和一条边对应相等,那么这两个三角形一定全等吗?
引导学生对 “两角一边” 的位置关系进行分类讨论,得出两种情况:两角及其夹边对应相等;两角及其中一角的对边对应相等(为后续学习 “AAS” 埋下伏笔)。
探究两角及其夹边对应相等的情况
操作实验:
让学生在练习本上画一个△ABC,使∠A = 60°,AB = 4cm,∠B = 45°。具体画图步骤如下:
画线段 AB = 4cm;
以点 A 为顶点,AB 为一边,画∠MAB = 60°;
以点 B 为顶点,BA 为一边,画∠NBA = 45°,射线 AM 与射线 BN 相交于点 C。
学生完成画图后,用剪刀剪下自己画的三角形,与同桌的三角形进行叠合比较,观察能否完全重合。
小组讨论:组织学生在小组内交流自己的发现,讨论通过这种方式画出的三角形是否全等。
归纳总结:
邀请几个小组代表发言,分享小组讨论结果。
教师根据学生的回答进行总结:经过大量的实验和验证可知,两角及其夹边对应相等的两个三角形全等。这就是三角形全等的 “角边角” 判定定理,简写成 “ASA”。
用几何语言表示为:在△ABC 和△DEF 中,
\(\begin{cases}∠A = ∠D\\AB = DE\\∠B = ∠E\end{cases}\),
所以△ABC ≌△DEF(ASA)。
(三)例题讲解(15 分钟)
例 1:已知:如图,在△ABC 和△DEF 中,∠A = ∠D,AB = DE,∠B = ∠E,求证:△ABC ≌△DEF。
分析:
明确题目中直接给出了满足 “角边角” 判定定理的三个条件。
按照 “角边角” 的顺序,将对应条件清晰罗列。
证明:在△ABC 和△DEF 中,
\(\begin{cases}∠A = ∠D\\AB = DE\\∠B = ∠E\end{cases}\)
所以△ABC ≌△DEF(ASA)。
例 2:已知:如图,点 B、F、C、E 在同一条直线上,FB = CE,∠B = ∠E,∠ACB = ∠DFE,求证:△ABC ≌△DEF。
分析:
由已知 FB = CE,根据等式性质,可得 FB + FC = CE + FC,即 BC = EF。
此时,在△ABC 和△DEF 中,有∠B = ∠E,BC = EF,∠ACB = ∠DFE,满足 “角边角” 判定定理的条件。
证明:
因为 FB = CE,
所以 FB + FC = CE + FC,即 BC = EF。
在△ABC 和△DEF 中,
\(\begin{cases}∠B = ∠E\\BC = EF\\∠ACB = ∠DFE\end{cases}\)
所以△ABC ≌△DEF(ASA)。
强调:
运用 “角边角” 判定定理证明三角形全等时,要严格按照两角及其夹边的顺序准确列出三个条件,并且对应顶点的字母必须写在对应的位置上。
注意观察图形,挖掘题目中隐含的条件,如通过线段的和差关系得到对应边相等,利用对顶角相等、公共角等得到对应角相等。
(四)课堂练习(10 分钟)
已知:如图,∠1 = ∠2,∠3 = ∠4,求证:△ABC ≌△ABD。
如图,在△ABC 中,AD⊥BC 于点 D,BE⊥AC 于点 E,AD 与 BE 相交于点 F,且∠CAD = ∠CBE,AC = BC,求证:△ADC ≌△BEC。
已知:如图,AB∥CD,AF = CE,∠B = ∠D,求证:△ABF ≌△CDE。
学生独立完成练习,教师巡视指导,及时发现并纠正学生在证明过程中出现的问题,如条件罗列顺序错误、对应顶点字母书写不规范等。选取部分学生的答案进行展示和点评,针对共性问题进行集中讲解。
(五)课堂小结(5 分钟)
与学生一起回顾本节课所学内容:
“角边角”(ASA)判定定理:两角及其夹边对应相等的两个三角形全等,明确其几何语言表述。
证明三角形全等的思路和步骤:先分析已知条件,找出满足 “角边角” 判定定理的对应角和对应边;再指明在哪两个三角形中进行全等证明;最后按照定理要求列出条件,得出结论。
强调运用 “角边角” 判定定理时的注意事项,如条件的顺序、对应顶点的书写以及挖掘隐含条件的重要性。
鼓励学生分享本节课的学习收获和体会,包括对知识的理解、学习方法的掌握以及在小组合作中的感受等。教师进行补充和总结,进一步强化重点内容,解答学生的疑问。
(六)布置作业(5 分钟)
必做题:教材课后练习题第 X 题、第 X 题,帮助学生巩固本节课所学的基础知识和基本技能。
选做题:已知:如图,在四边形 ABCD 中,AB∥CD,∠B = ∠D,求证:△ABC ≌△CDA,提高学生运用知识解决综合性问题的能力。
拓展题:如图,在△ABC 和△A'B'C' 中,∠A = ∠A',∠B = ∠B',BC = B'C',试探究△ABC 与△A'B'C' 是否全等,并说明理由,引导学生思考 “角角边” 与 “角边角” 的联系,为后续学习做铺垫 。
五、教学反思
在本节课教学中,通过多种教学方法引导学生探究 “角边角” 判定定理,注重学生的动手操作和思维训练。但在教学过程中,可能存在部分学生对定理的应用不够灵活,在复杂图形中难以快速准确找到对应条件的情况。在今后的教学中,应增加更多不同类型、不同难度层次的练习题,加强对学生分析问题和解决问题能力的培养。同时,进一步关注学生在小组合作中的参与度和表现,确保每个学生都能在合作学习中有所收获和提高。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1、通过画图、操作、实验等教学活动,探索三角形全等的判定方法(A.S.A.,A.A.S.);
2、会用A.S.A.,A.A.S.判定两个三角形全等;
3、灵活地运用所学的判定方法判定两个三角形全等,从而解决线段或角相等的问题;
温故知新
上节课,我们得到了全等三角形的一种判定方法,还记得吗?
S.A.S.
现在我们讨论两角一边的情况:如果两个三角形有两个角、一条边分别对应相等,那么这两个三角形全等吗?
(角边角)
(角角边)
可以分成两种情况:(1)两个角及这两角的夹边;
(2)两个角及其中一角的对边.
问题:如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带哪一块去呢?你能帮这位同学出主意吗?
知识点一 角边角判定三角形全等
操作1:如图,用纸板挡住了两个三角形的一部分,你能画出这两个三角形吗?如果能,你画的三角形与其他同学画的三角形能完全重合吗?
相当于已知一角画三角形,我们可以画出无数个不同形状、大小的三角形.
三角形能唯一确定.
4
60°
45°
F
E
D
4
45°
60°
A
B
C
4
60°
R
Q
P
操作2:如图,△ABC与△QPR、 △DEF能完全重合吗?动手试一试.
(实验手册附录D)
45°
操作3:按下列作法,用直尺和圆规作△ABC,使AB=a, ∠A=∠α, ∠B=∠β,
1你作的三角形与其他同学作的三角形能完全重合吗?你有什么发现?
作法:
1.作AB=a.
2.在AB的同一侧分别作∠MAB=∠α ,∠NBA=∠β ,AM、BN相交于点C.
3.分别连接AB、AC.
△ABC就是所求作的三角形.
α
a
小组交流验证.
β
知识要点
“角边角”判定方法
文字语言:两角及其夹边分别相等的两个三角形全等(简写成“角边角”或“A.S.A.”).
几何语言:
∠A=∠A′ (已知),
AB=A′ B′ (已知),
∠B=∠B′ (已知),
在△ABC和△A′ B′ C′中,
∴ △ABC≌△ A′ B′ C′ (ASA).
A
B
C
A ′
B ′
C ′
典例精析
例1、如图,已知∠ABC=∠DCB,∠ACB = ∠DBC.
求证: △ABC ≌△DCB,AB = DC.
解:在△ABC 和△DCB 中,
∵∠ABC =∠DCB (已知),
BC = CB(公共边),
∠ACB = ∠DBC(已知),
∴△ABC≌△DCB( A.S.A. ).
∴AB = DC(全等三角形的对应边相等).
例2 已知:如图,在△ABC中,D是BC的中点,点E、F分别在AB、AC上,且DE//AC,DF//AB.
求证:BE=DF,DE=CF.
E
A
B
C
D
F
证明:∵DE∥AC,DF∥AB(已知),
∴∠EDC=∠C,∠B=∠FDC (两直线平行,同位角相等).
∵D是线段BC的中点(已知),
∴BD=DC(线段中点定义).
在△EBD和△FDC中,
∴△EBD≌△FDC(ASA),
∴BE=DF,DE=CF(全等三角形对应边相等).
练一练
1.如图,∠C=∠E,∠1=∠2,BA=DA,你能证明BC=DE吗
A
E
D
C
B
1
2
证明:∵ ∠1=∠2 (已知),
∴ ∠1+∠DAC=∠2+∠DAC (等式性质),
∴ ∠BAC=∠DAE.
在△BAC和△DAE中,
∴△BAC≌△DAE(ASA),
∴AC=DE(全等三角形的对应边相等).
2.已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C
(1)求证:△ABE≌△ACD
A
B
C
D
E
O
解:(1)证明 :在△ADC和△AEB中
∴△ACD≌△ABE(ASA)
(2) ∵△ACD≌△ABE(已证)
∴AD=AE(全等三角形的对应边相等)
又∵AB=AC(已知)
∴AB-AD=AC-AE(等式性质)
∴BD=CE
(2) BD和CE相等吗
知识点二 角角边判定三角形全等
(角角边)
如图,如果两个三角形有两个角分别对应相等,且其中一组相等的角的对边相等,那么这两个三角形是否一定全等?
思 考
分析:因为三角形的内角和等于180°,因此有两个角对应相等,那么第三个角必定对应相等,于是有“角边角”,可证得这两个三角形全等.
已知:如图,∠A=∠A′,∠B=∠B′,AC=A′C′.
求证: △ABC≌△A′B′C′.
证明:∵∠A=∠A′,∠B=∠B′,
∠A+∠B+∠C=180°,
∠A′+∠B′+∠C′=180°(三角形内角和等于180°),
∴∠C=∠C′(等量代换).
在△ABC和△A′B′C′中,
∵∠A=∠A′,
AC=A′C′,
∠C=∠C′,
∴△ABC≌△A′B′C′(A.S.A.)
知识要点
“角角边”判定方法
文字语言:有两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“A.A.S.”).
几何语言:
∠A=∠A′ (已知),
∠B=∠B′ (已知),
AC=A′ C′ (已知),
在△ABC和△A′ B′ C′中,
∴ △ABC≌△ A′ B′ C′ (A.A.S.).
A
B
C
A ′
B ′
C ′
典例精析
例3 如图,点D在AB上,点E在AC上,AD=AE, ∠B=∠C,
求证:AB=AC.
A
B
C
D
E
分析:证明△ACD≌△ABE,就可以得出AB=AC.
证明:在△ACD和△ABE中,
∠A=∠A(公共角 ),
∠C=∠B (已知 ),
AD=AE(已知),
∴ △ACD≌△ABE(A.A.S.),
∴AB=AC.
方法归纳:通常利用全等三角形的对应边相等来证明两条线段相等,这是一个重要的方法.类似的方法可以证明两个角相等.
例4.已知:如图, AB⊥BC,AD⊥DC,∠1=∠2, 求证:AB=AD.
A
C
D
B
1
2
证明: ∵ AB⊥BC,AD⊥DC,
∴ ∠ B=∠D=90 °.
在△ABC和△ADC中,
∠1=∠2 (已知),
∠ B=∠D(已证),
AC=AC (公共边),
∴ △ABC≌△ADC(A.A.S.).
∴AB=AD.
练一练
1、如图,在△ABC中,D 是边 BC 的中点,过点C 画直线 CE,使 CE// AB,交 AD 的延长线于点 E.求证: AD = ED.
证明: CE // AB (已知),
∵∠ABD = ∠ECD,∠BAD = ∠CED (两直线平行,内错角相等).
在△ABD 与 △ECD 中,
∵∠ABD = ∠ECD,∠BAD = ∠CED (已证),
BD = CD (已知),
∴△ABD≌△ECD ( A.A.S. ) ,
∴AD = ED (全等三角形的对应边相等).
D
A
C
B
证明:(已知)
∴________________(两直线平行,内错角相等)
又(已知)
∴_________________(等式的性质)
在和中
(________)
(全等三角形的对应边相等).
∠ADB=∠CBD
∠ABD=∠CDB
∠ADB=∠CBD
BD=DB
∠ABD=∠CDB
ASA
1.如图,已知.请将下列说明的理由补充完整.
1. 打碎的一块三角形玻璃如图所示,现在
要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
A. 带①④去 B. 带②③去 C. 带③④去 D. 带②④去
√
返回
(第2题)
2. [2025武汉江夏区期中]如图,在
和中,点,, 在同
一直线上,已知 ,
,添加以下条件后,仍不能
判定 的是( )
A. B.
C. D.
√
返回
(第3题)
3. 如图,在中, ,
,于点,于点 ,
,,则 的长是( )
A. B.
C. D.
√
(第3题)
【点拨】 , ,
,
,
, ,
.
在和 中,
,
, ,
.
(第3题)
返回
4.如图,已知,由尺规作图痕迹可知 ,
全等的理由为_____.
(第4题)
返回
5.如图,点,,,在同一条直线上, ,
,.若 , ,则
的度数为_____ .
110
(第5题)
(第5题)
【点拨】, .在
和 中,
,
,
.
返回
6. 如图,,,,
四点在一条直线上, ,
,老师说:再添加一个条件就
可以使 .下面是课堂上
(1)甲、乙、丙三个同学说法正确的是________;
甲、丙
三个同学的发言,甲说:添加 ,乙说:添加
;丙说:添加 .
(2)请你从正确的说法中选择一种,给出你的证明.
【解】(二选一即可)选择甲.证明如
下:
, .
在和中,
.
或选择丙.证明如下:
, .
,.在和 中,
.
返回
7. 在中, ,将
沿图中虚线剪开,剪下的两个三角形不一定全等的是
( )
A. B. C. D.
√
角边角
判定定理
角边角
应用角边角、角角边判定三角形全等
应用
角角边
应用角边角、角角边解决问题
谢谢观看!
